مجموع زوایای داخلی هشت ضلعی و هشت ضلعی منتظم – با مثال

مجموع زوایای داخلی هشت ضلعی و هشت ضلعی منتظم برابر 1080 درجه است. اگر قصد یادگیری نحوه محاسبه این عدد و جمع زاویه های داخلی انواع هشت ضلعی‌ها (منتظم، نامنتظم، محدب و مقعر) را دارید، با این آموزش همراه باشید. در این مقاله از مجله فرادرس، فرمول و نحوه محاسبه مجموع زوایای داخلی هشت ضلعی را به همراه حل چندین مثال متنوع آموزش می‌دهیم.

هشت ضلعی چیست ؟

هشت ضلعی، یکی از اشکال هندسی چند ضلعی است که از هشت ضلع و هشت راس تشکیل می‌شود.

تصویر زیر، نمونه‌ای از یک هشت ضلعی را نمایش می‌دهد. اندازه ضلع‌ها و زاویه‌های هشت ضلعی می‌تواند برابر یا نابرابر باشد.

هشت ضلعی منتظم چیست ؟

به چندضلعی‌هایی که همه ضلع‌ها و زوایه‌هایشان با هم مساوی هستند، چند ضلعی منتظم گفته می‌شود. بر اساس این تعریف، هشت ضلعی منتظم، شکلی است که هشت ضلع و هشت زاویه برابر دارد. تصویر زیر، نمونه‌ای از یک هشت ضلعی منتظم را نمایش می‌دهد.

زاویه داخلی چیست ؟

زاویه داخلی، زاویه بین ضلع‌های مجاور اشکال هندسی چند ضلعی است که درون محیط آن‌ها قرار می‌گیرد. در تصویر زیر، زوایای داخلی و خارجی یک هشت ضلعی نمایش داده شده است.

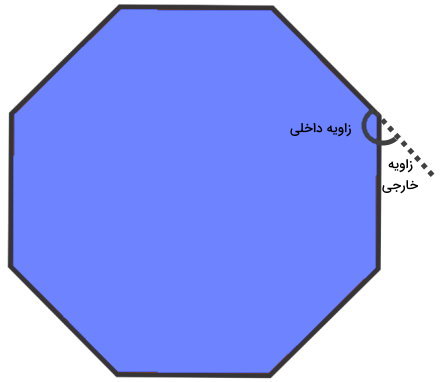
مجموع زوایای داخلی چگونه بدست می آید ؟

مجموع زوایای داخلی اشکال هندسی، بر اساس تعداد ضلع‌های آن به دست می‌آید. رابطه جبری بین تعداد ضلع‌های چند ضلعی و مجموع زوایای داخلی آن به صورت زیر نوشته می‌شود:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها

بر اساس رابطه بالا، مجموع زوایای داخلی برخی از چند ضلعی‌ها برابر است با:

• مجموع زوایای داخلی سه ضلعی: 180 درجه
• مجموع زوایای داخلی چهار ضلعی: 360 درجه
• مجموع زوایای داخلی پنج ضلعی: 540 درجه
• مجموع زوایای داخلی شش ضلعی: 720 درجه
• مجموع زوایای داخلی هفت ضلعی: 900 درجه

مجموع زوایای داخلی هشت ضلعی چقدر است ؟

مجموع زوایای داخلی هشت ضلعی برابر با 1080 درجه است. این عدد با استفاده از فرمول مجموع زوایای داخلی چند ضلعی‌ها نیز به دست می‌آید:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی هشت ضلعی
• n: تعداد ضلع‌ها برابر 8

$$S = (8-2) \times 180°$$

$$S = (6) \times180°$$

$$S = 1080°$$

تصویر زیر، یک هشت ضلعی منتظم و زاوایای داخلی آن را نمایش می‌دهد.

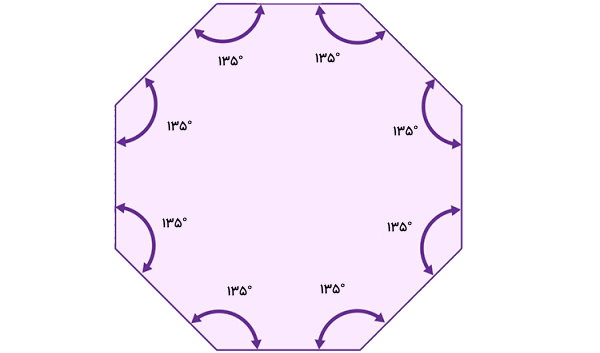
مجموع زوایای داخلی هشت ضلعی بالا برابر است با:

1080° = زاویه هشتم + ... + زاویه دوم + زاویه اول

1080° = A + B + ... + H

اندازه هر زاویه داخلی هشت ضلعی منتظم چند است؟

اندازه تمام زوایای هشت ضلعی منتظم با یکدیگر برابر است. بنابراین، اگر اندازه زاویه داخلی یک راس را برابر با A در نظر بگیریم، خواهیم داشت:

$$A+A+A+A+A+A+A+A= 1080°$$

$$8A= 1080°$$

$$A= \frac {1080°} {8}$$

$$A= 135°$$

در نتیجه، اندازه هر یک از زوایای داخلی یک هشت ضلعی منتظم برابر با 135 درجه است.

مثال مجموع زوایای داخلی هشت ضلعی

در این بخش، چند مثال متنوع را در زمینه محاسبه مجموع زوایای داخلی هشت ضلعی حل می‌کنیم.

مثال 1: تعیین اندازه زاویه و نوع هشت ضلعی از روی مجموع زوایای داخلی

مجموع هفت زاویه داخلی یک هشت ضلعی برابر 950 درجه است. اندازه زاویه هشتم را تعیین کنید. آیا این هشت ضلعی منتظم است؟

برای تعیین زاویه هشتم، رابطه مجموع زوایای داخلی آن را می‌نویسیم:

1080° = مجموع زوایای داخلی هشت ضلعی

1080° = زاویه هشتم + مجموع هفت زاویه

1080° = زاویه هشتم + °950

950° - 1080° = زاویه هشتم

130° = زاویه هشتم

زاویه هشتم هشت ضلعی برابر 80 درجه است. از آنجایی که این زاویه برابر با 135 درجه نیست، هشت ضلعی از نوع منتظم نیست.

مثال 2: محاسبه مجموع چند زاویه داخلی هشت ضلعی

اندازه چهار زاویه داخلی یک هشت ضلعی نامنظم معلوم است. مجموع چهار زاویه دیگر هشت ضلعی را حساب کنید.

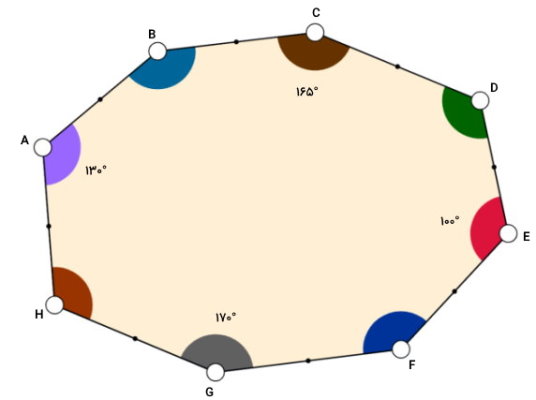
بر اساس تصویر بالا، مجموع زوایای داخلی شکل برابر است با:

$$A+B+C+D+E+F+E+H = 1080°$$

زوایه‌های معلوم را درون رابطه بالا قرار می‌دهیم:

$$130°+B+165°+D+100°+F+170°+H = 1080°$$

$$565°+B+D+F+H = 1080°$$

$$B+D+F+H = 1080° -565°$$

$$B+D+F+H = 515°$$

مجموع چهار زاویه دیگر هشت ضلعی برابر 570 درجه است.

مثال 3: مجموع زوایای داخلی مثلث های درون هشت ضلعی

راس‌های هشت ضلعی زیر را با استفاده از چند پاره‌خط غیر متقاطع به یکدیگر متصل کرده‌ایم. مجموع زوایای داخلی هر مثلث و مجموع زوایای داخلی تمام مثلث‌ها را حساب کنید. عدد به دست آمده چه رابطه‌ای با مجموع زوایای داخلی هشت ضلعی دارد؟

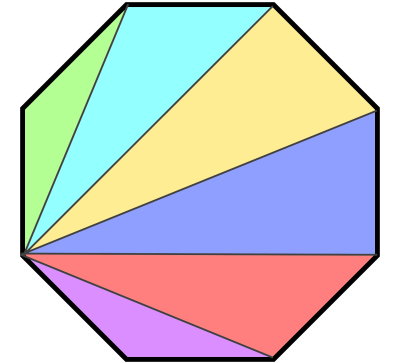
مجموع زوایای داخلی مثلث برابر 180 درجه است. این مقدار از رابطه زیر به دست می‌آید:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی مثلث
• n: تعداد ضلع‌های مثلث برابر 3

$$S = (3-2) \times 180°$$

$$S = (1) \times 180°$$

$$S = 180°$$

هشت ضلعی بالا از شش مثلث تشکیل شده است. در نتیجه، مجموع زوایای داخلی تمام مثلث‌ها برابر است با:

$$6 \times 180° = 1080°$$

مجموع تمام مثلث‌ها برابر با 1080 درجه یا همان مجموع زوایای داخلی هشت ضلعی شد. از این مثال می‌توان دریافت که می‌توان تمام چند ضلعی‌ها را به مجموعه‌ای از چند مثلث تبدیل کرد و مجموع زاویه های داخلی آن‌ها را با شمارش تعداد مثلث‌ها و ضرب این عدد در 180 به دست آورد. البته نحوه ایجاد مثلث‌ها، باید دقیقا مثلث تصویر این مثال (از مبدا یکی از راس‌ها) باشد.

مثال 4: محاسبه مجموع زوایای داخلی هشت ضلعی با استفاده از زویای خارجی

هشت ضلعی زیر را با پنج زاویه داخلی و سه زاویه خارجی معلوم را در نظر بگیرید. مجموع زوایای داخلی هشت ضلعی را با محاسبه تمام زاویه‌ها به دست بیاورید. سپس، مجموع زوایای خارجی این هشت ضلعی را محاسبه کنید.

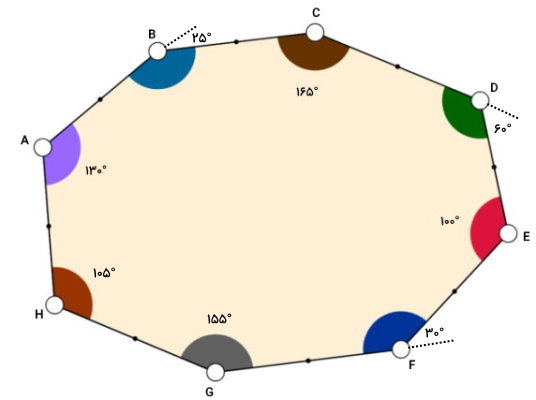
برای محاسبه مجموع زوایای داخلی، نیاز به تعیین سه زاویه داخلی مجهول داریم. این زوایا، با استفاده از زاویه خارجی مجاورشان محاسبه می‌شوند. مجموع هر زاویه داخلی و خارجی یک راس برابر 180 درجه است. بنابراین، داریم:

$$B = 180° - 25° = 155°$$

$$D = 180° - 60° = 120°$$

$$F = 180° - 30° = 150°$$

اکنون تمام زوایای داخلی را داریم. مجموع زوایای داخلی هشت ضلعی برابر خواهد بود با:

$$A+B+C+D+E+F+E+H$$

$$130° + 155° + 165°+ 120°+ 100°+ 150°+ 155° + 105°$$

$$1080°$$

در نتیجه، مجموع زوایای داخلی هشت ضلعی برابر 1080 درجه است. برای به دست آوردن مجموع زوایای خارجی هشت ضلعی، ابتدا باید هر یک از زاویه‌های خارجی را تعیین کنیم. زوایای خارجی راس‌های A تا H به ترتیب برار هستند با:

$$180° - 130° = 50°$$

$$25°$$

$$180° - 1165° = 15°$$

$$60°$$

$$180° - 100° = 80°$$

$$30°$$

$$180° - 155° = 25°$$

$$180° - 105° = 75°$$

اکنون، تمام زاویه های خارجی بالا را با هم جمع می‌کنیم:

$$50° + 25° + 15°+ 60°+ 80°+ 30°+ 25° + 75°$$

$$50° + 25° + 15°+ 60°+ 80°+ 30°+ 25° + 75°$$

$$360°$$

مجموع زوایای خارجی هشت ضلعی برابر 360 درجه است. البته در صورت انجام محاسبات بر روی چند ضلعی‌های دیگر، متوجه خواهید شد که مجموع زوایای خارجی تمام چند ضلعی‌های بسته برابر 360 است. به عنوان مثال، در مطلب «مجموع زوایای داخلی ذوزنقه»، این موضع برای چهار ضلعی‌ها مورد بررسی قرار گرفته است.

مثال 5: مجموع زوایای داخلی هشت ضلعی مقعر

تصویر زیر، یک هشت ضلعی مقعر را نمایش می‌دهد. در این شکل هندسی، حداقل یکی از زاویه‌های داخلی بزرگ‌تر از 180 درجه است. مجموع زاویه‌های داخلی این هشت ضلعی را حساب کنید.

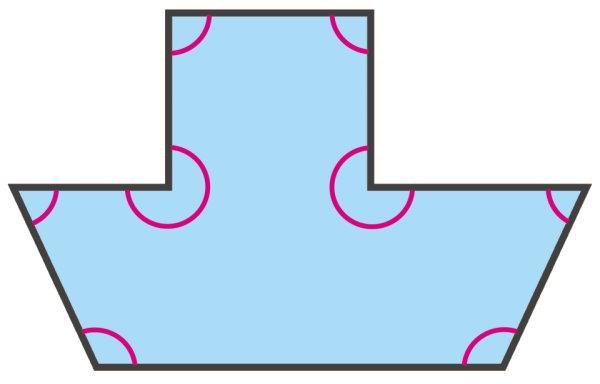
مجموع زاویه های داخلی هشت ضلعی، هیچ تفاوتی با مجموع زاویه های داخلی هشت ضلعی محدب (تمام مثال‌های قبلی این مقاله) ندارد. تنها پارامتر مهم در اندازه‌گیری مجموع زوایای داخلی، تعداد ضلع‌ها است. بنابراین، مجموع زوایای داخلی هشت ضلعی مقعر نیز مطابق با فرمول زیر برابر 1080 درجه خواهد بود:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی مثلث
• n: تعداد ضلع‌های هشت ضلعی مقعر برابر 8

$$S = (8-2) \times 180°$$

$$S = (6) \times 180°$$

$$S = 1080°$$

سوالات متداول در رابطه با زوایای داخلی هشت ضلعی

در این مطلب از مجله فرادرس در مورد مجموع زوایای داخلی هشت ضلعی و هشت ضلعی منظم صحبت کردیم. در ادامه، به برخی از سوالات پرتکرار در رابطه با زاویه های داخلی هشت ضلعی، به طور مختصر پاسخ می‌دهیم.

هشت ضلعی چند زاویه داخلی و چند زاویه خارجی دارد؟

همان طور که از اسمش پیداست، هشت ضلعی دارای 8 ضلع و 8 زاویه داخلی است.

مجموع زاویه های داخلی هشت ضلعی چند است ؟

مجموع زوایای داخلی هشت ضلعی برابر 1080 درجه است.

مجموع زاویه های خارجی هشت ضلعی چقدر است ؟

مجموع زوایای خارجی هشت ضلعی برابر با 360 درجه است.

اندازه هر زاویه داخلی هشت ضلعی منتظم چقدر است ؟

اندازه هر زاویه داخلی هشت ضلعی منتظم برابر 135 درجه است.

فرمول مجموع زاویه های داخلی هشت ضلعی چیست ؟

فرمول مجموع زوایای داخلی هشت ضلعی برابر °180 × (n-2) است که در آن، n، تعداد ضلع‌های هشت ضلعی را نمایش می‌دهد.

مجموع زاویه داخلی و خارجی هشت ضلعی چقدر است؟

جمع زاویه داخلی یک راس هشت ضلعی با زاویه خارجی همان راس، برابر 180 درجه است. مجموع تمام زوایای داخلی و خارجی هشت ضلعی برابر 1440 درجه است.