قطاع دایره چیست؟ – فرمول های محاسبه محیط و مساحت + حل مثال و تمرین
قطاع دایره شکلی متشکل از دو شعاع و یک کمان است. اگر از روی دو نقطه بر روی محیط دایره، دو شعاع رسم کنیم، دایره به دو قطاع بزرگ و کوچک تقسیم میشود. در این آموزش، به معرفی ویژگیها، اجزا و فرمولهای محاسبه محیط و مساحت قطاع دایره به همراه حل چند مثال میپردازیم.


دایره از چه اجزایی تشکیل میشود؟
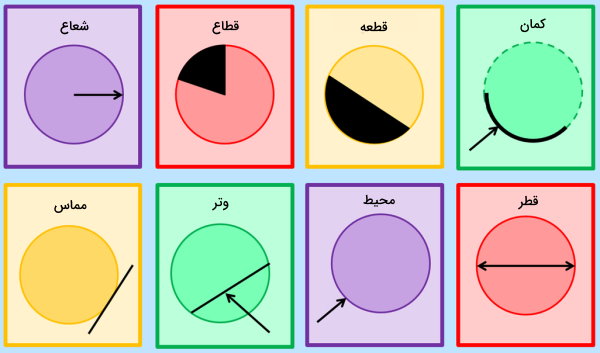
نقطهای بر روی یک صفحه را در نظر بگیرید. اگر در اطراف این نقطه، مجموعهای از نقاط پیوسته را با یک فاصله ثابت از آن رسم کنیم، دایره تشکیل میشود. به اندازه دور دایره، محیط آن میگویند. دایره اجزای مختلفی دارد که میتوانید مهمترین آنها را در تصویر زیر مشاهده کنید.
قطاع دایره چیست؟
«قطاع» (Sector)، ناحیهای از دایره است که به دو شعاع و یک کمان محدود میشود. تصویر زیر، دو قطاع دایره را نمایش میدهد.
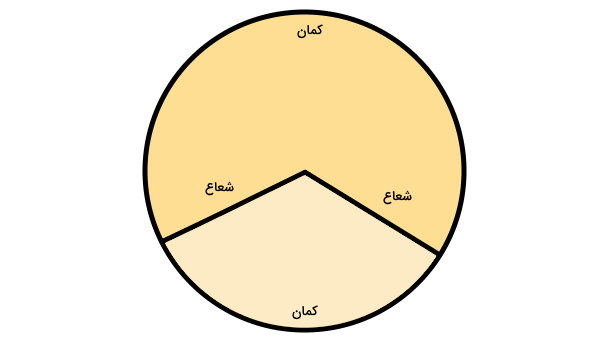
اجزای قطاع دایره چه هستند؟
هر قطاع دایره از یک کمان و دو شعاع تشکیل میشود:
- کمان: منحنی محدود به دو نقطه بر روی محیط دایره
- شعاع: فاصله بین هر نقطه بر روی دایره تا مرکز آن
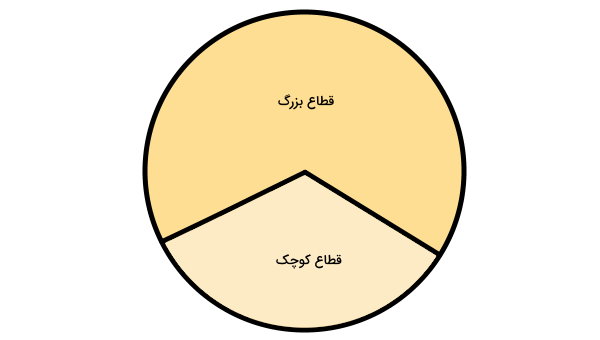
بر اساس تعاریف ارائه شده، هر دو شعاع دایره، آن را به دو قطاع بزرگ و کوچک تقسیم میکنند. فقط در یک حالت خاص (نیمدایره)، دایره به دو قطاع برابر تقسیم میشود.
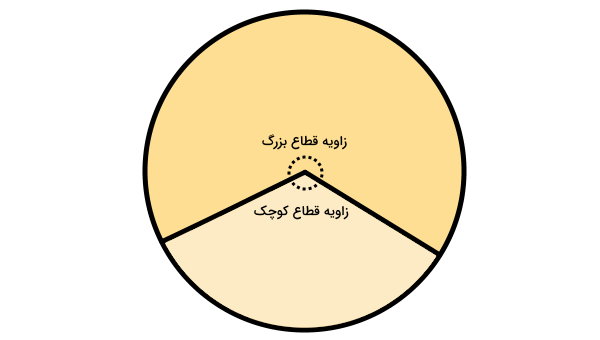
زاویه مرکزی قطاع دایره چیست؟
به زاویه بین دو شعاع قطاع، زاویه مرکزی میگویند. این زاویه در محاسبه محیط و مساحت قطاع مورد استفاده قرار میگیرد.
تفاوت قطاع و قطعه دایره در چیست؟
یکی دیگر از تعاریف مربوط به دایره، قطعه است. در برخی از موارد، به دلیل شباهت اسمی، قطاع و قطعه دایره با یکدیگر اشتباه گرفته میشوند. قطعه، ناحیه محدود به یک وتر و یک کمان است. شکل زیر، یک قطاع را نمایش میدهد. 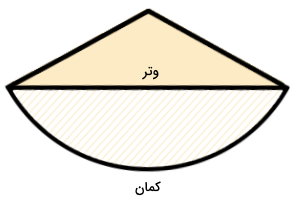
بخش هاشور خورده قطاع بالا، یکی از قطعههای دایره است. همانطور که مشاهده میکنید؛ مساحت این قطعه، بخشی از مساحت کل قطاع است. در بخشهای بعدی، نحوه محاسبه مساحت قطعه با استفاده از مساحت قطاع را آموزش میدهیم.
محیط یا طول قطاع دایره چیست؟
در هندسه، اندازه دور هر شکل دوبعدی، با عنوان محیط آن شکل تعریف میشود. بر اساس همین تعریف، محیط قطاع دایره، طول اجزای تشکیل دهنده آن است.
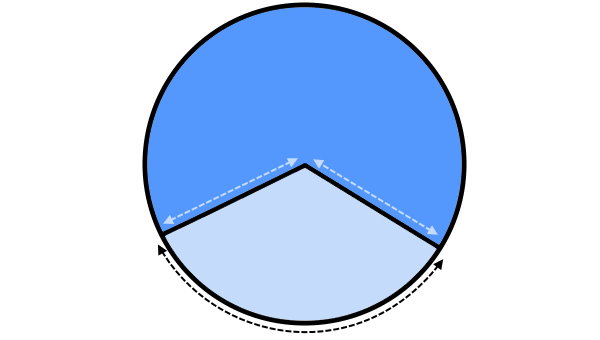
بر اساس تصویر بالا، محیط قطاع از رابطه زیر به دست میآید:
شعاع + شعاع + کمان = محیط قطاع
(شعاع × 2) + کمان = محیط قطاع
طول کمان قطاع دایره چگونه بدست میآید؟
کمان دایره، بخشی از محیط آن است. فرمول محیط دایره به صورت زیر نوشته میشود:
شعاع × عدد پی × 2 = محیط دایره
زاویه یک دایره کامل، برابر 360 درجه یا ۲π است. عبارت «عدد پی × ۲» در رابطه بالا، زاویه یک دایره کامل را نمایش میدهد. بنابراین اگر بخواهیم طول کمان دایره را بدست بیاوریم، میتوانیم نسبت زاویه مرکزی مقابل آن به زاویه کامل را در محیط دایره ضرب کنیم. با توجه به مطالب گفته شده، شکل ساده شده رابطه طول کمان دایره عبارت است از:
زاویه کمان × شعاع = طول کمان
عبارت جبری رابطه بالا معمولا به صورت زیر نوشته میشود:
- l: طول کمان
- r: شعاع دایره
- θ: زاویه کمان بر حسب رادیان
اندازه زاویه بر حسب رادیان است. البته در اغلب موارد، زاویه، با واحد درجه اندازهگیری و بیان میشود. به همین دلیل، باید برای تبدیل واحد درجه به رادیان، از رابطه زیر استفاده کنیم:
180 ÷ (π × درجه) = رادیان
پس تعیین طول کمان و جمع آن با اندازه شعاعها، محیط قطاع به دست میآید.
مثال 1: محاسبه طول قطاع دایره
زاویه مرکزی قطاعی به شعاع 4 واحد، برابر 45 درجه است. طول قطاع را حساب کنید.
منظور از طول قطاع، همان محیط یا اندازه دور آن است. با توجه به صورت مسئله، اندازه زاویه را بر حسب درجه داریم. برای تعیین محیط، باید این اندازه را به رادیان تبدیل کنیم:
180 ÷ (π × درجه) = رادیان
180 ÷ (۳/۱۴ × 45) = رادیان
180 ÷ (۱۴۱/۳) = رادیان
۰/۷۸۵ = رادیان
این زاویه به منظور تعیین طول کمان قطاع مورد استفاده قرار میگیرد:
۰/۷۸۵ × 4 = طول کمان
۳/۱۴ = طول کمان
فرمول محیط قطاع به صورت زیر نوشته میشود:
(شعاع × 2) + کمان = محیط قطاع
(۴ × 2) + ۳/۱۴ = محیط قطاع
(۸) + ۳/۱۴ = محیط قطاع
۱۱/۱۴ = محیط قطاع
در نتیجه، محیط قطاع دایره برابر ۱۱/۱۴ واحد طول است.
مساحت قطاع دایره چیست؟
مساحت، اندازه سطحی است که داخل یک شکل بسته قرار میگیرد. مساحت قطاع، سطح محدود به کمان و شعاعهای آن را نمایش میدهد.
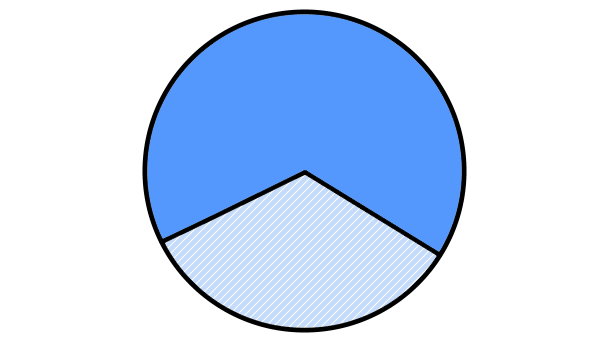
همانطور که مشاهده میکنید، مساحت هر قطاع دایره، بخش یا نسبتی از مساحت دایره کامل است.
مساحت قطاع دایره چگونه بدست میآید؟
فرمول مساحت دایره به صورت زیر نوشته میشود:
شعاع × شعاع × عدد پی = مساحت دایره
مساحت قطاع، نسبتی از رابطه بالا است. این نسبت، به زاویه مقابل کمان قطاع بستگی دارد. به طور کلی، مساحت قطاع دایره از فرمول زیر به دست میآید:
نصف زاویه مرکزی × شعاع × شعاع = مساحت قطاع
عبارت جبری یا فرمول ریاضی مساحت قطاع دایره معمولا به صورت زیر نوشته میشود:
- A: مساحت قطاع
- r: شعاع
- α: زاویه مرکزی بر حسب رادیان
مثال 2: محاسبه مساحت قطاع دایره با نسبت
زاویه مرکزی یک قطاع برابر 30 درجه است. اگر شعاع این قطاع برابر 12 سانتیمتر باشد، مساحت آن چقدر خواهد بود؟ (محاسبات را تا دو رقم اعشار انجام دهید.)
سادهترین روش برای محاسبه مساحت قطاع، تعیین نسبت زاویه مرکزی به زاویه دایره کامل است:
مساحت دایره کامل از رابطه زیر به دست میآید:
شعاع × شعاع × عدد پی = مساحت دایره
12 × ۱۲ × ۳/۱۴ = مساحت دایره
۴۵۲/۱۶ = مساحت دایره
اگر مساحت دایره کامل را در نسبت به دستآمده ضرب کنیم، مساحت قطاع محاسبه میشود:
مساحت دایره × نسبت زاویه مرکزی = مساحت قطاع
۴۵۲/۱۶ × ۰/۰۸ = مساحت قطاع
۳۶/۱۷ = مساحت قطاع
در نتیجه، مساحت قطاع برابر ۳۶/۱۷ سانتیمتر مربع است.
مثال 3: محاسبه مساحت قطاع دایره با فرمول
مساحت قطاع مثال 2 را با فرمول مخصوص آن به دست بیاورید. (محاسبات را تا دو رقم اعشار انجام دهید.)
فرمول مخصوص مساحت قطاع به صورت زیر نوشته میشود:
- A: مساحت قطاع
- r: شعاع برابر 12
- α: زاویه مرکزی بر حسب رادیان
در قدم اول، زاویه را از درجه به رادیان تبدیل میکنیم:
180 ÷ (π × درجه) = رادیان
180 ÷ (۳/۱۴ × 30) = رادیان
180 ÷ (۹۴/۲) = رادیان
۰/۵۲ = رادیان
این عدد را به همراه شعاع، درون فرمول مساحت قرار میدهیم:
مساحت قطاع برابر ۳۷/۴۴ سانتیمتر مربع است. اگر دقت کنید، متوجه خواهید شد که مساحتهای به دست آمده از دو روش با یکدیگر تفاوت دارند. دلیل این اختلاف، خطای ناشی از گرد کردن اعداد تا اعشار دلخواه است. اگر تعداد رقمهای اعشار در محاسبات را بیشتر کنیم، این دو عدد به یکدیگر نزدیک میشوند. در نتیجه، هنگام حل مسائل مربوط به مساحت، حتما به این موضوع دقت کنید.
انواع قطاع دایره چه هستند؟
در بخشهای قبلی دیدیم که با رسم هر دو شعاع دایره، دو قطاع بزرگ و کوچک تشکیل میشود. به این ترتیب، امکان رسم قطاعهای دلخواه با اندازههای متفاوت وجود دارد. با این وجود، مساحت برخی از قطاعها، نسبت خاصی از مساحت دایره کامل است.
از انواع قطاع شناخته شده، میتوان به نیم دایره، ثلث دایره، ربع دایره و خمس دایره اشاره کرد. این قطاعها به ترتیب، یکدوم، یکسوم، یکچهارم و یکپنجم دایره کامل هستند.
نیم دایره چیست؟
اگر یک دایره را در راستای قطرش، به دو قسمت تقسیم کنیم، دو قطاع هماندازه ایجاد میشود. به این دو قطاع، نیمدایره میگویند.
نیمدایره، یکی از قطعههای دایره نیز به شمار میرود. زاویه مرکزی این قطاع، 180 درجه است.

محیط و مساحت نیم دایره
محاسبه محیط و مساحت نیمدایره، یک تفاوت ویژه با قطاعهای دیگر دارد. به دلیل مشخص بودن نسبت نیمدایره به دایره کامل، فرمول محیط و مساحت این قطاع به صورت زیر نوشته میشود:
قطر + نصف محیط دایره = محیط نیمدایره
نصف مساحت دایره = مساحت نیمدایره
همانطور که مشاهده میکنید، در فرمولهای بالا، اثری از زاویه مرکزی کمان نیست. البته مفهوم این زاویه، به صورت غیرمستقیم و در عبارت «نصف» آورده شده است (نسبت زاویه نیمدایره، نصف زاویه دایره کامل است).
مثال 4: محاسبه محیط و مساحت نیمدایره
شعاع یک دایره برابر 19 متر است. با رسم وتری به اندازه 38 متر، این دو را به قطعه تقسیم میکنیم. محیط و مساحت هر قطعه را تعیین کنید.
اندازه وتر در این مسئله، دو برابر شعاع یا برابر قطر دایره است. قطر، دایره را به قطاع برابر (نیمدایره) تقسیم میکند. محیط هر قطاع نیمدایره از رابطه زیر به دست میآید:
قطر + نصف محیط دایره = محیط نیمدایره
محیط دایره کامل برابر است با:
قطر × عدد پی = محیط دایره
۳۸ × ۳/۱۴ = محیط دایره
۱۱۹/۳۲ = محیط دایره
بنابراین، نصف محیط دایره برابر خواهد بود با:
۲ ÷ محیط دایره = نصف محیط دایره
۲ ÷ ۱۱۹/۳۲ = نصف محیط دایره
۵۹/۶۶ = نصف محیط دایره
این عدد را به همراه قطر، در رابطه محیط نیمدایره قرار میدهیم:
38 + 59/66 = محیط نیمدایره
97/66 = محیط نیمدایره
محیط هر قطعه برابر ۹۷/۶۶ متر است. مساحت نیمدایره از رابطه زیر محاسبه میشود:
نصف مساحت دایره = مساحت نیمدایره
مساحت یک دایره کامل توسط فرمول زیر محاسبه میشود:
شعاع × شعاع × عدد پی = مساحت دایره
۱۹ × ۱۹ × ۳/۱۴ = مساحت دایره
۱۱۳۳/۵۴ = مساحت دایره
از اینرو، برای مساحت نیمدایره داریم:
۲ ÷ مساحت دایره = مساحت نیمدایره
۲ ÷ ۱۱۳۳/۵۴ = مساحت نیمدایره
۵۶۶/۷۷ = مساحت نیمدایره
در نتیجه، مساحت هر قطعه برابر ۵۶۶/۷۷ متر مربع است. توجه داشته باشید که فقط در این مثال (مسئله نیمدایره)، میتوانیم از اصلاح قطعه و قطاع به جای یکدیگر استفاده کنیم.
ربع دایره چیست؟
با تقسیم دایره به چهار قسمت مساوی، چهار قطاع به وجود میآید که به آنها، ربع دایره میگویند. مساحت هر ربعدایره، برابر یکچهارم مساحت دایره کامل بوده و زاویه مرکزی آن برابر 90 درجه است.
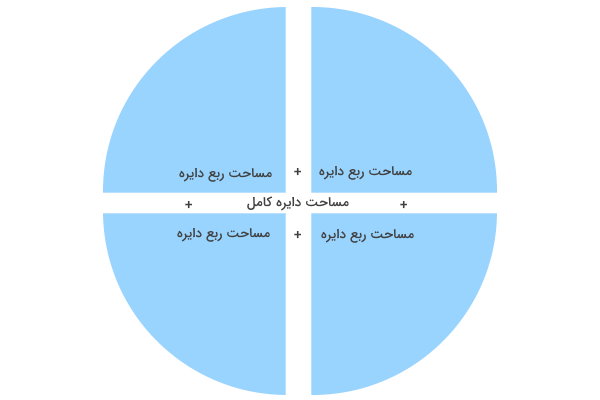
محیط و مساحت ربع دایره
محیط و مساحت ربعدایره با استفاده از فرمولهای زیر محاسبه میشوند:
(شعاع × 2) + یکچهارم محیط دایره = محیط ربعدایره
یکچهارم مساحت دایره = مساحت ربعدایره
مثال 5: محاسبه محیط و مساحت ربعدایره
زاویه مرکزی یک قطاع برابر 90 درجه است. اگر قطر دایره کامل این قطاع برابر 28 میلیمتر باشد، محیط و مساحت قطاع چقدر خواهد بود؟
زاویه قطاع برابر 90 درجه یا یکچهارم زاویه دایره کامل است. بنابراین، این قطاع، یک ربعدایره محسوب میشود. به منظور محیط و مساحت ربعدایره، به محیط و مساحت دایره کامل آن نیاز داریم. محیط دایره برابر است با:
قطر × عدد پی = محیط دایره
۲۸ × ۳/۱۴ = محیط دایره
۸۷/۹۲ = محیط دایره
مساحت دایره نیز با فرمول زیر تعیین میشود:
شعاع × شعاع × عدد پی = مساحت دایره
به جای شعاع، نصف قطر (14=2÷28) را قرار میدهیم:
14 × 14 × ۳/۱۴ = مساحت دایره
۶۱۵/۴۴ = مساحت دایره
اکنون میتوانیم محیط و مساحت ربعدایره را حساب کنیم. با توجه به فرمول محیط ربعدایره، داریم:
(شعاع × 2) + یکچهارم محیط دایره = محیط ربعدایره
(14 × 2) + (4 ÷ ۸۷/۹۲) = محیط ربعدایره
(۲۸) + (۲۱/۹۸) = محیط ربعدایره
۴۹/۹۸ = محیط ربعدایره
محیط ربعدایره برابر ۴۹/۹۸ میلیمتر است. مساحت ربعدایره نیز با استفاده از فرمول زیر به دست میآید:
یکچهارم مساحت دایره = مساحت ربعدایره
4 ÷ مساحت دایره = مساحت ربعدایره
4 ÷ ۶۱۵/۴۴ = مساحت ربعدایره
۱۵۳/۸۶ = مساحت ربعدایره
در نتیجه، مساحت ربعدایره برابر ۱۵۳/۸۶ میلیمتر مربع است.
محاسبه مساحت قطعه
در بخشهای قبلی اشاره کردیم که مساحت قطعه، با استفاده از فرمول مساحت قطاع و فرمول مساحت مثلث محاسبه میشود. برای درک این موضوع، قطعه زیر را در نظر بگیرید.
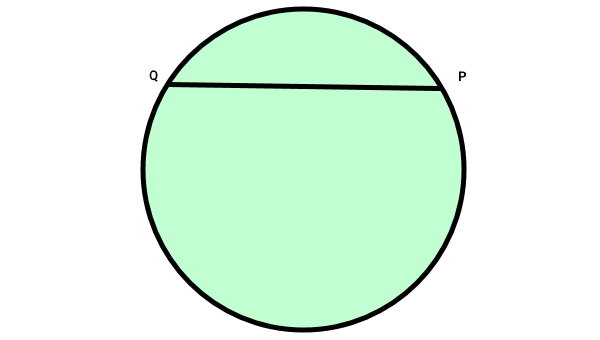
با رسم دو شعاع از نقاط P و Q، یک قطاع با کمان QP و یک مثلث (OPQ) تشکیل میشود.
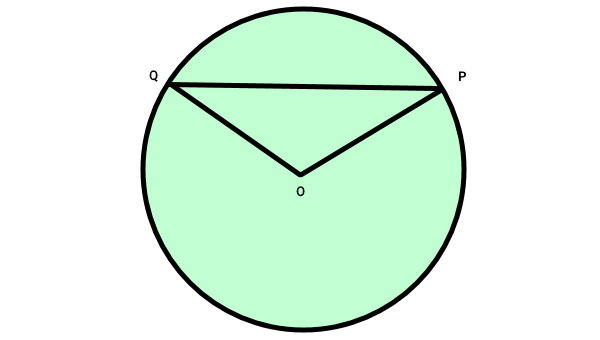
اگر مساحت مثلث را از مساحت قطاع کم کنیم، مساحت قطعه به دست میآید.
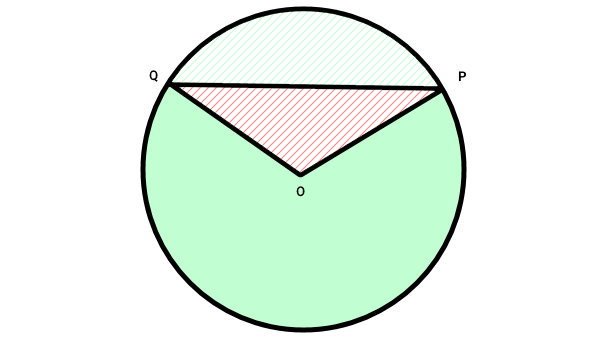
فرمول مساحت قطعه عبارت است از:
یا
- A: مساحت قطعه
- r: شعاع
- θ: زاویه قطاع بر حسب رادیان
مثال 6: محاسبه مساحت قطعه دایره
مساحت قطعهای به شعاع 10 و زاویه مرکزی 75 درجه را حساب کنید.
فرمول مساحت قطعه عبارت است از:
- A: مساحت قطعه
- r: شعاع برابر 10
- θ: زاویه قطاع بر حسب رادیان (زاویه 75 درجه برابر 1/31 رادیان است.)
سینوس زاویه 75 درجه نیز برابر ۰/۹۷ است:
در نتیجه، مساحت قطعه برابر ۱۷ واحد سطح است.
مرکز جرم قطاع دایره کجاست؟
مرکز جرم، نقطهای فرضی است که در آن، توزیع نیرو نسبت به تمام نقاط دیگر جسم در حالت تعادل قرار دارد. مرکز جسم بهترین گزینه برای نمایش جسمهای مختلف به صورت نقطهای در صفحه یا فضا است. به عنوان مثال، نقطه M در تصویر زیر، مرکز جرم قطاع را نمایش میدهد.
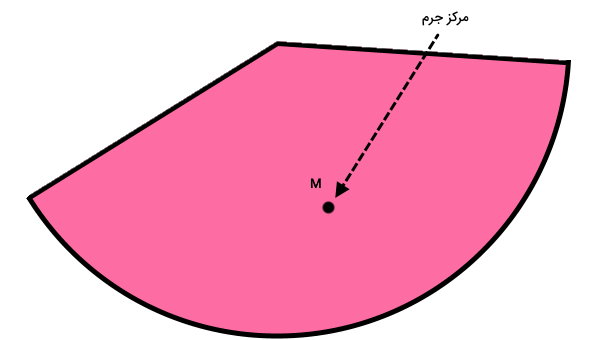
اگر مرکز مختصات را برابر (0 ,0) در نظر بگیریم، مختصات x مرکز جرم قطاع دایره از رابطه زیر به دست میآید:
مختصات y مرکز جرم نیز از رابطه زیر محاسبه میشود:
فاصله مرکز جرم قطاع از مرکز دایره نیز برابر است با:
- d: فاصله مرکز دایره تا مرکز جرم قطاع
- R: شعاع قطاع
- α: نصف زاویه مرکز بر حسب درجه
محاسبه آنلاین قطاع دایره
امروزه، ابزارهای اینترنتی بسیاری وجود دارند که امکان تعیین اندازههای مختلف شکلهای هندسی را فراهم میکنند. به عنوان مثال، محاسبهگرهای سایت Omni Calculator (+)، ابزارهای مناسبی برای تعیین اندازههای شکلهای هندسی از جمله نیمدایره هستند. تصویر زیر، محاسبهگر آنلاین مساحت و طول کمان قطاع در سایت Omni Calculator را نمایش میدهد.
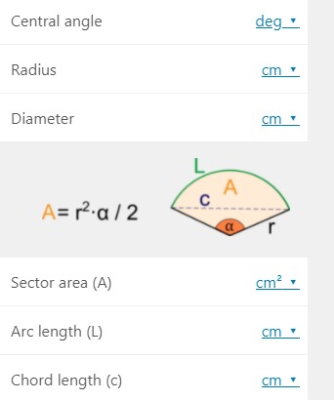
در ماشین حساب بالا، با وارد کردن اندازههایی نظیر زاویه مرکزی و شعاع یا قطر، مساحت قطاع، طول کمان و اندازه وتر متناظر آن محاسبه میشود.
سوالات متداول در رابطه با قطاع دایره
در این بخش، به برخی از سوالات پرتکرار در رابطه با قطاع دایره به طور خلاصه پاسخ میدهیم.
تعریف قطاع دایره چیست؟
قطعه دایره، بخشی از دایره است که از دو شعاع و یک کمان تشکیل میشود.
دایره چند قطاع دارد؟
دایره، بیشمار قطاع دارد.
دایره چند قطاع یک درجهای دارد؟
اگر دایره را به قطاعهای یک درجهای تبدیل کنیم، 360 قطاع به وجود میآید.
آیا نیم دایره یک قطاع است؟
بله. نیمدایره یکی از قطاعهای خاص دایره است که از یک قطر (دو شعاع) و یک کمان (نصف محیط) تشکیل میشود.
آیا ربع دایره یک قطاع است؟
بله. ربعدایره، قطاع به اندازه یکچهارم دایره است.
کدام شکل هم قطعه دایره و هم قطاع دایره است؟
نیمدایره، هم یک قطاع و هم یک قطعه از دایره محسوب میشود.
قطاع و قطعه دایره چه فرقی دارند؟
قطعه دایره، بخش محدود به یک وتر و یک کمان دایره است؛ در صورتی که قطاع، به دو شعاع و یک کمان محدود میشود.
محاسبه محیط قطاع دایره چگونه انجام میشود؟
محیط قطاع دایره از جمع طول کمان دایره و اندازه دو شعاع آن به دست میآید.
مساحت قطاع دایره چقدر است؟
مساحت قطاع دایره، حاصلضرب نسبت زاویه مرکزی آن به زاویه دایره در مساحت دایره است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش های بدست آوردن محیط و مساحت دایره + حل تمرین و تمامی فرمول ها» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- دایره چیست ؟ — تعریف و مفاهیم به زبان ساده
- شعاع چیست ؟ — شعاع دایره به زبان ساده
- وتر چیست ؟ — به زبان ساده
- عدد پی (Π) چیست ؟ — کاربردها به زبان ساده
- قطاع و مقطع دایره و محاسبات آن در هندسه — به زبان ساده
- محیط دایره به زبان ساده + حل تمرین و فیلم آموزش رایگان
- مساحت دایره به زبان ساده + حل تمرین
- فرمول محیط دایره چیست ؟ + حل تمرین و مثال
- فرمول مساحت دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- نسبت محیط دایره به قطر آن چیست ؟ — به زبان ساده
- نسبت محیط دایره به شعاع آن چیست ؟ — به زبان ساده
- مساحت نیم دایره چگونه بدست می آید ؟ — به زبان ساده + حل مثال
- مساحت ربع دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محاسبه محیط دایره آنلاین — بهترین سایت ها + حل تمرین
- محیط نیم دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط ربع دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محاسبه گر مساحت دایره آنلاین — بهترین سایت ها + حل تمرین و مثال
- محیط و مساحت دایره چیست ؟ — به زبان ساده + حل تمرین و مثال
- محیط دایره با چی متناسب است ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط و مساحت دایره چیست ؟ — به زبان ساده + حل مثال
- دایره چند شعاع دارد ؟ — تصویری و به زبان ساده
- مماس دایره چیست و چه ویژگی هایی دارد؟ — به زبان ساده + حل تمرین و مثال
- کمان دایره چیست ؟ — محاسبه طول و اندازه + حل مثال
- قطر دایره چیست ؟ — رسم و محاسبه قطر + حل تمرین و مثال
- قطعه دایره چیست ؟ — فرمول محیط و مساحت + حل مثال
- قطاع دایره چیست ؟ — فرمول های محاسبه محیط و مساحت + حل مثال و تمرین(همین مطلب)













سلام لطفا در خصوص بدست آوردن نیم دایره ای که مثلا قطر15 و ارتفاع 5 دارد راهنمائی کنید با تشکر
با سلام و وقت بخیر؛
منظور شما از ارتفاع نیمدایره چیست؟ محاسبه یا تعیین چه پارامتری از نیمدایره مد نظر شما است؟