قرینه شکل چیست؟ – به زبان ساده + مثال و حل تمرین

قرینه شکل، شکلی است که در اثر بازتاب شکل اصلی نسبت به یک خط یا یک نقطه به وجود می‌آید. به عنوان مثال، اگر جسمی را در مقابل آینه قرار دهیم، قرینه آن جسم درون آینه به نمایش درمی‌آید. روش‌های مختلفی برای رسم قرینه اشکال مختلف وجود دارد. در این مقاله، ابتدا به تعریف قرینه شکل و مفاهیم مرتبط با آن‌ها می‌پردازیم. سپس، روش‌های رسم قرینه اشکال هندسی مختلف را به همراه مثال‌های تصویری آموزش می‌دهیم.

تقارن در هندسه چیست ؟

«تقارن» (Symmetry)، یک مفهوم ریاضی است که اغلب در مورد شکل‌های هندسی بیان می‌شود. اگر یک شکل را در معرض تبدیلات هندسی نظیر انتقال، دوران، بازتاب و تجانس قرار دهیم و آن شکل هیچ تغییری نکند، می‌گوئیم شکل دارای تقارن یا اصطلاحا «متقارن» (Symmetrical) است.

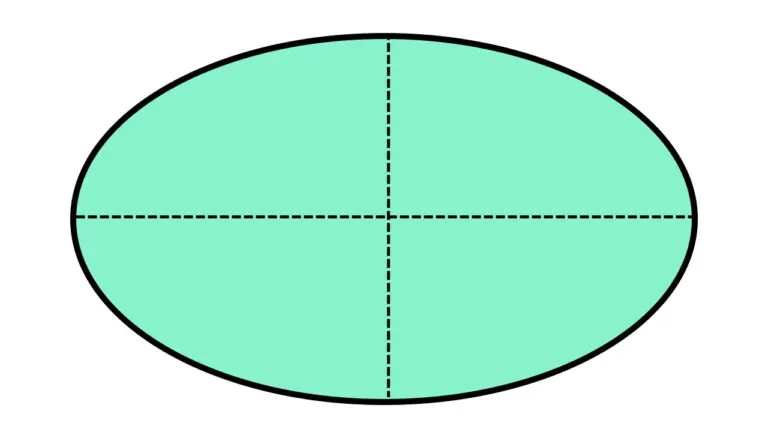
به شکل‌های بدون تقارن، شکل‌های «نامتقارن» (Asymmetrical) گفته می‌شود. در تصویر زیر، یک شکل متقارن و یک شکل نامتقارن را نمایش می‌دهد.

انواع تقارن چه هستند ؟

تقارن، معمولا به سه نوع تقارن انتقالی، چرخشی و بازتابی (محوری) تقسیم می‌شوند. در ادامه، به معرفی هر یک از این تقارن‌ها می‌پردازیم.

تقارن انتقالی چیست ؟

هرگاه شکلی را در جهت دلخواه جابجا کنیم بدون این‌که هیچگونه تغییری در مشخصات دیگر آن رخ دهد، می‌گوئیم آن شکل تقارن انتقالی دارد.

تقارن محوری چیست ؟

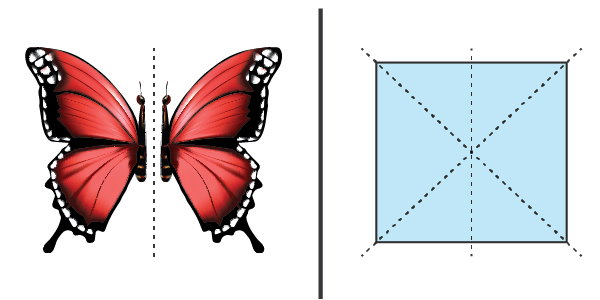
هرگاه شکلی را از روی یک خط تا کنیم و هر دو طرف شکل بر روی هم منطبق شوند، می‌گوییم آن شکل تقارن محوری دارد. به خطی که شکل را از روی آن تا زدیم، خط تقارن یا محور تقارن گفته می‌شود. دو طرف محور تقارن، قرینه یا بازتاب یکدیگرند. به همین دلیل، تقارن محوری با عنوان تقارن بازتابی نیز شناخته می‌شود. در تصویر زیر می‌‌توانید دو نمونه از تقارن محوری را مشاهده کنید. تقارن محوری، به طور مستقیم با مفهوم قرینه شکل نسبت به یک خط ارتباط دارد.

تقارن چرخشی چیست ؟

هرگاه شکلی را حول نقطه‌ای بچرخانیم و شکل بر روی خودش منطبق شود، می‌گوییم آن شکل تقارن چرخشی یا تقارن دورانی دارد. به تعداد انطباق شکل بر روی خودش در یک دور کامل، مرتبه تقارن چرخشی گفته می‌شود. به عنوان مثال، تصویر متحرک زیر، تقارن چرخشی مرتبه سوم در یک مثلث متساوی‌الاضلاع را نمایش می‌دهد.

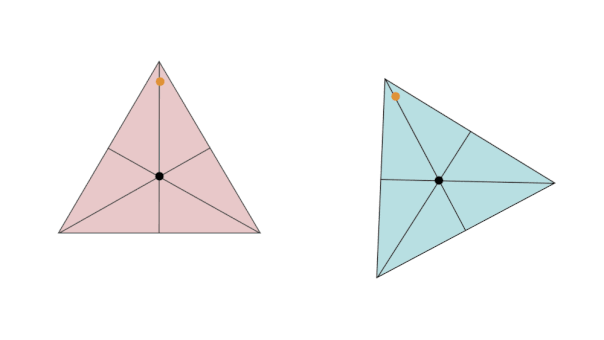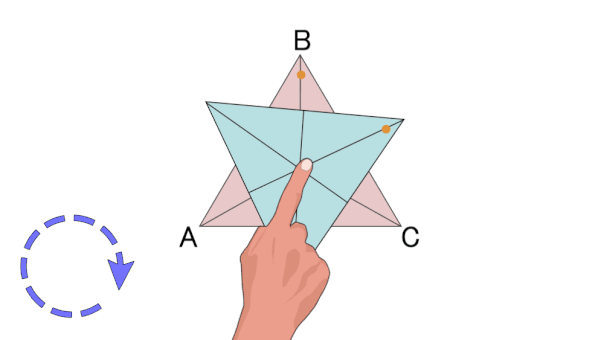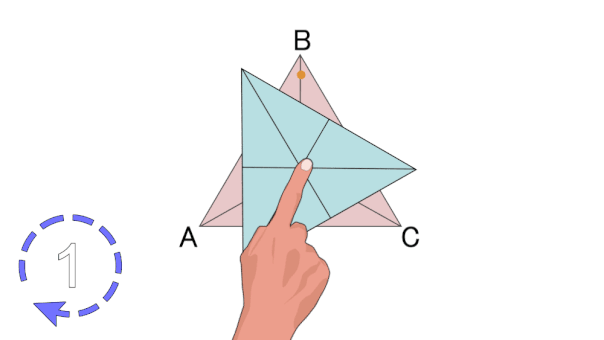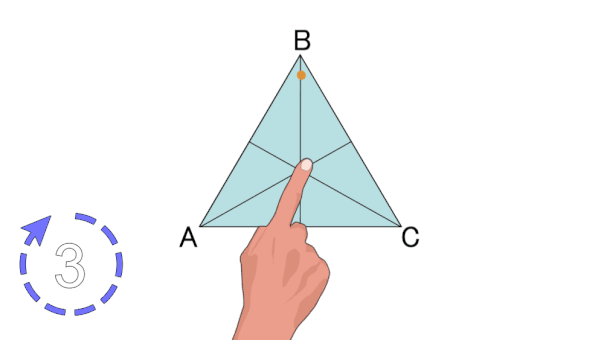
تقارن محوری و تقارن مرکزی، از انواع تقارن چرخشی به شمار می‌روند. اگر شکلی تقارن چرخشی داشته باشد، قطعا تقارن محوری، تقارن مرکزی یا هر دوی این تقارن‌ها را نیز دارد. مثلث متساوی‌الاضلاع بالا، دارای سه محور تقارن است اما مرکز تقارن ندارد.

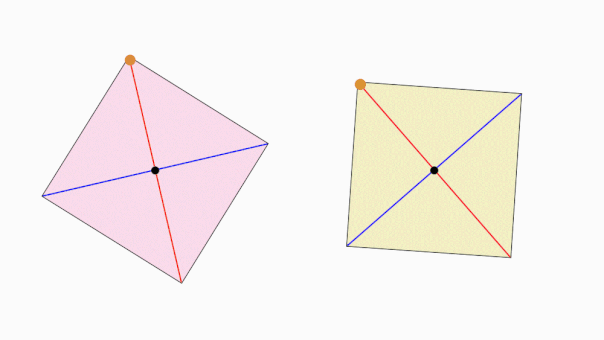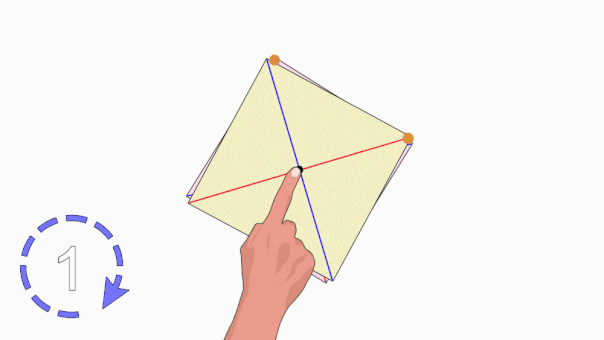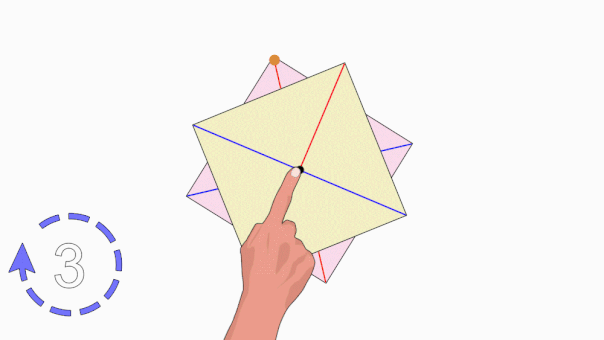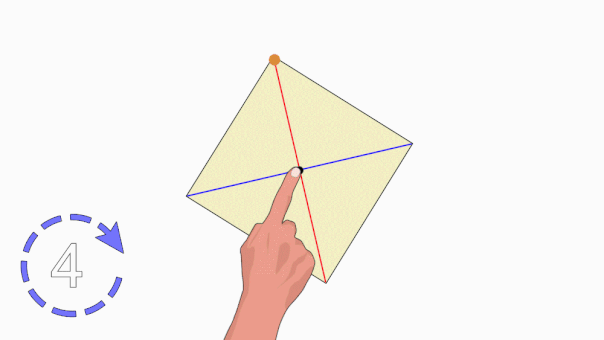
هنگام دوران مربع حول یک نقطه مرکزی، در یک دور کامل، این شکل، چهار بار بر روی خودش منطبق می‌شود. مربع، هم دارای محور تقارن و هم دارای مرکز تقارن است.

تقارن مرکزی چیست ؟

هرگاه شکلی را نیم‌دور (180 درجه) حول نقطه‌ای بچرخانیم و شکل روی خودش منطبق شود، می‌گوییم آن شکل تقارن مرکزی یا تقارن نقطه‌ای دارد. به نقطه‌ای که شکل را حول آن چرخاندیم، مرکز تقارن گفته می‌شود. تقارن مرکزی، همان تقارن چرخشی مرتبه دوم است. برای رسم قرینه شکل نسبت به یک نقطه، از مفهوم تقارن مرکزی استفاده می‌کنیم.

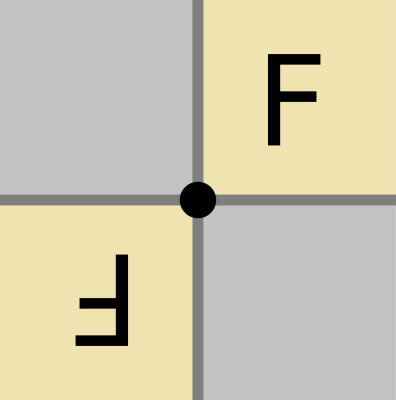
تقارن محوری و تقارن مرکزی، به طور مستقیم با مبحث قرینه شکل ارتباط دارند. از این‌رو، در صورت تمایل به یادگیری بیشتر راجع به این مفاهیم، مطالعه مطالب زیر را به شما پیشنهاد می‌کنیم:

• تقارن محوری در اشکال دوبعدی — به زبان ساده (+ دانلود فیلم آموزش رایگان)
• تقارن محوری چیست؟ — به زبان ساده + مثال و فیلم آموزشی
• تقارن مرکزی چیست؟ — به زبان ساده + مثال و فیلم آموزشی
• تقارن چرخشی در اشکال دوبعدی — به زبان ساده (+ دانلود فیلم آموزش رایگان)
• محور تقارن چند ضلعی منتظم چیست؟ — به زبان ساده

قرینه شکل چیست؟

اگر بازتاب شکلی را نسبت به یک خط یا نقطه رسم کنیم، قرینه شکل به وجود می‌آید. ابعاد قرینه یک شکل، هیچ تفاوتی با ابعاد اصلی آن شکل ندارد.

برای درک مفهوم قرینه شکل، یک آینه را در نظر بگیرید. آینه، تصویر اجسام را بازتاب می‌دهد. از این‌رو، تصویر به وجود آمده در آن، قرینه شکل اجسام است.

یکی دیگر از مثال‌های تشکیل قرینه شکل، بازتاب تصویر اجسام در آب است. تصویر زیر، نمونه‌ای از بازتاب و قرینه شکل‌ها در طبیعت را نمایش می‌دهد. قرینه شکل‌ها، معمولا نسبت به یک خط یا یک نقطه رسم می‌شود. در ادامه به توضیح هر یک از این موارد می‌پردازیم.

اگر می‌خواهید قرینه یک شکل رسم شده بر روی کاغذ نسبت به یک خط را مشاهده کنید، کاغذ را از روی خط تا بزنید و آن را در مقابل نور بگیرید. به این ترتیب، قرینه شکل قابل مشاهده خواهد بود.

قرینه شکل نسبت به یک خط

در بخش‌های قبلی، با تعریف تقارن محوری و خط تقارن آشنا شدیم. قرینه شکل نسبت به یک خط، همان تقارن محوری است. تصویر زیر، یک مثلث را بر روی صفحه شطرنجی نمایش می‌دهد.

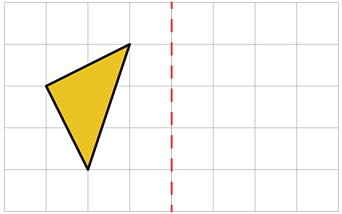
اگر مثلث بالا را نسبت به خط‌چین قرمز بازتاب دهیم، قرینه آن به صورت زیر به وجود می‌آید.

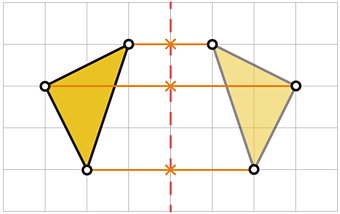
هنگام رسم بازتاب یک شکل، فاصله هر نقطه قرینه تا خط تقارن، به اندازه فاصله نقطه متناظر آن در شکل اصلی تا خط تقارن خواهد بود.

قرینه شکل نسبت به یک نقطه

قرینه شکل نسبت به یک نقطه، همان تقارن مرکزی است. تصویر زیر، یک مثلث و قرینه آن را نسبت به یک نقطه نمایش می‌دهد. به ازای هر یک از راس‌های مثلث، یک راس قرینه وجود دارد. فاصله هر راس تا مرکز تقارن، با فاصله مرکز تقارن تا قرینه آن راس برابر است.

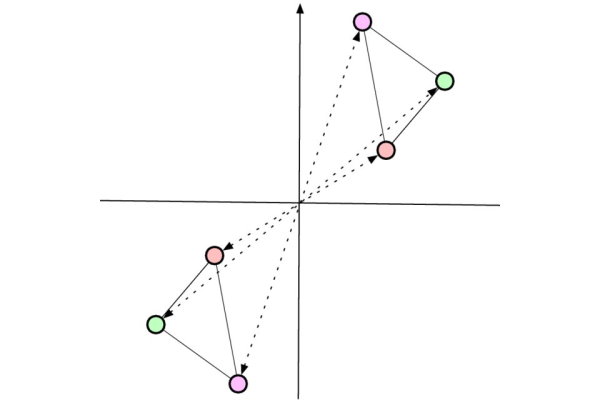
اگر مثلث را حول مرکز تقارن به اندازه 180 درجه دوران دهیم، اجزای آن به طور کامل بر روی شکل قرینه منطبق می‌شود. به عبارت دیگر، قرینه شکل، حاصل تقارن مرکزی (تقارن چرخشی مرتبه دوم) است.

رسم قرینه شکل چگونه انجام می شود ؟

قرینه یک شکل، با توجه به خط یا نقطه تقارن رسم می‌شود. روش‌های مختلفی برای رسم قرینه شکل‌ها وجود دارد. ساده‌ترین روش، استفاده از صفحه شطرنجی یا محورهای مختصات است. صفحه شطرنجی زیر را در نظر بگیرید.

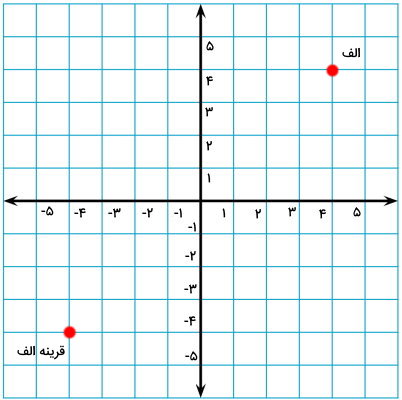
به منظور درک بهتر فرآیند رسم قرینه شکل، محورهای مختصات عمودی و افقی را بر روی صفحه شطرنجی رسم و اندازه‌گذاری کرده‌ایم. اکنون، نقطه‌ای مانند نقطه «الف» را بر روی صفحه شطرنجی در نظر بگیرید. قصد داریم قرینه نقطه الف را رسم کنیم.

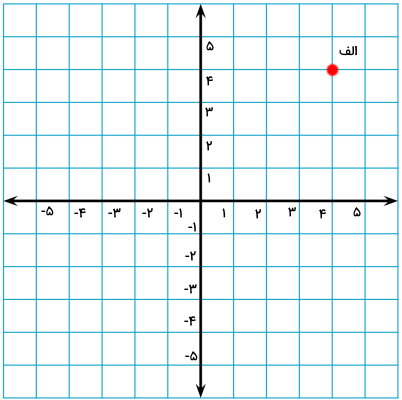
اولین سوالی که هنگام رسم قرینه شکل باید از خود بپرسید؛ این است که نقطه یا خط تقارن کجاست. تا زمانی که نقطه یا خط تقارن معلوم نباشد، امکان رسم قرینه وجود نخواهد داشت. در اینجا، می‌خواهیم قرینه نقطه الف را نسبت به محور عمودی، محور افقی و مرکز مختصات رسم کنیم. به منظور رسم قرینه نسبت به محور عمودی، باید فاصله نقطه تا این محور را به دست بیاوریم.

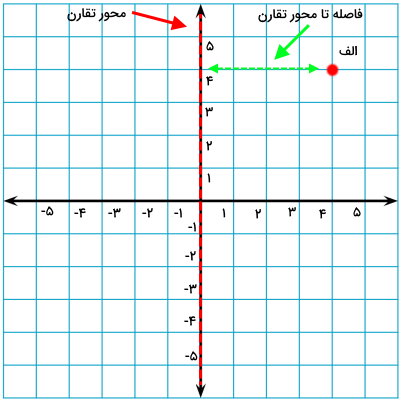
خانه‌های بین نقطه الف تا محور عمودی را می‌شماریم. تعداد این خانه‌ها برابر با 4 است. این عدد، فاصله بین نقطه الف تا محور تقارن را نمایش می‌دهد. پس از رسیدن به محور تقارن، به همین فاصله جلو (به سمت دیگر محور) می‌‌رویم.

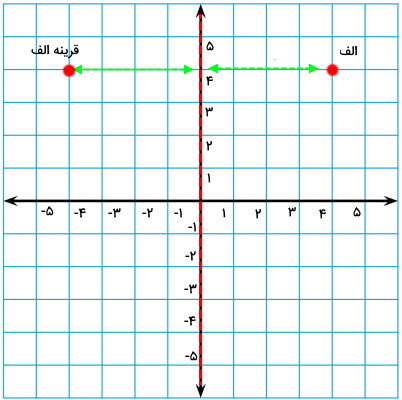
سپس، در فاصله 4 خانه از سمت دیگر محور تقارن، یک نقطه می‌گذاریم. این نقطه، «قرینه الف» است.

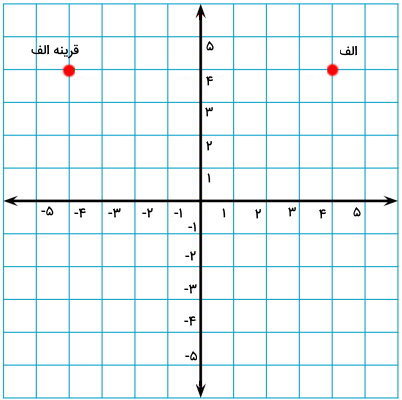
هنگام رسم قرینه نقطه نسبت به محور عمودی، ارتفاع (مختصات عمودی) آن تغییر نمی‌کند؛ اما عرض (مختصات افقی) آن قرینه (منفی) می‌شود. نقطه الف در تصویر بالا دارای مختصات (4,4) و قرینه آن دارای مختصات (4,4-) است. از این ویژگی می‌توان به منظور رسم سریع‌تر قرینه اشکال هندسی در دستگاه مختصات استفاده کرد.

برای رسم قرینه الف نسبت به محور افقی، همین مراحل را تکرار می‌کنیم. البته این بار، محور تقارن، تغییر می‌کند.

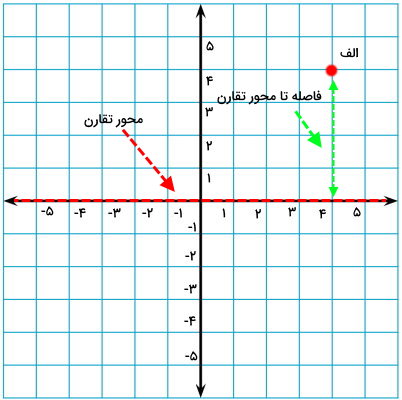
به این ترتیب، ابتدا فاصله بین نقطه الف تا محور تقارن (محور افقی) را اندازه می‌گیریم. این فاصله برابر با 4 است. سپس، به همین اندازه (4 واحد) در سمت دیگر محور، جلو می‌رویم.

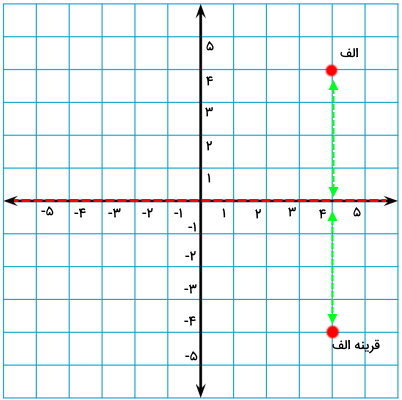
در فاصله 4 خانه از محور تقارن، محل قرارگیری قرینه الف را علامت می‌زنیم.

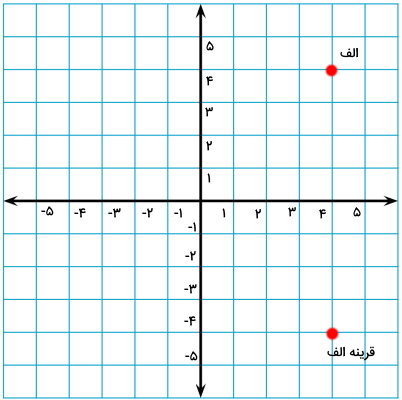
هنگام رسم قرینه نقطه نسبت به محور افقی، عرض (مختصات افقی) آن تغییر نمی‌کند؛ اما ارتفاع (مختصات عمودی) آن قرینه (منفی) می‌شود. نقطه الف در تصویر بالا دارای مختصات (4,4) و قرینه آن دارای مختصات (4-,4) است. در انتها، قصد داریم قرینه نقطه الف را نسبت به مرکز مختصات (محل برخورد محورهای عمودی و افقی) پیدا کنیم. به این منظور، ابتدا فاصله الف تا مختصات (0,0) را به دست می‌آوریم.

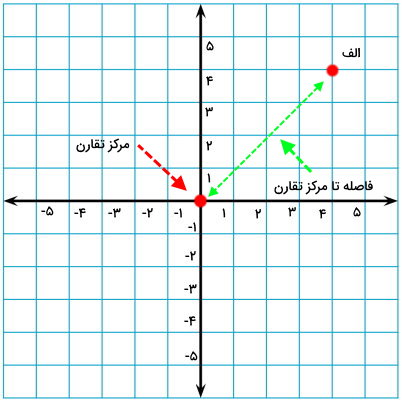
سپس، دقیقا به همان اندازه و در همان راستا، در طرف مقابل نقطه جلو می‌رویم.

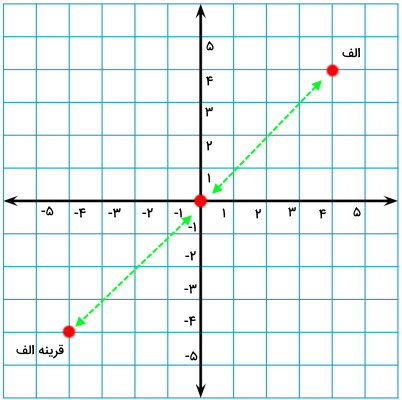
در طرف مقابل مرکز تقارن و در فاصله‌ای مشابه، قرینه الف را رسم می‌کنیم.

هنگام رسم قرینه نقطه نسبت به مرکز تقارن، عرض (مختصات افقی) و ارتفاع (مختصات عمودی)، قرینه (منفی) می‌شود. نقطه الف در تصویر بالا دارای مختصات (4,4) و قرینه آن دارای مختصات (4-,4-) است. رسم قرینه نسبت به خط مورب نیز با روشی مشابه با مثال‌های بالا انجام می‌شود. تنها باید فاصله عمودی نقاط شکل را تا خط مورد نظر به دست آورده و نقاط قرینه را در فاصله‌ای برابر در طرف دیگر خط رسم کنید. در ادامه، نحوه رسم را با چند مثال توضیح می‌دهیم.

مثال 1: رسم قرینه نسبت به خط تقارن افقی

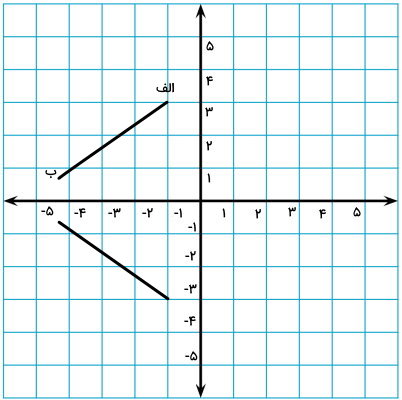
قرینه خط «الف ب» را نسبت به محور افقی مختصات پیدا کنید.

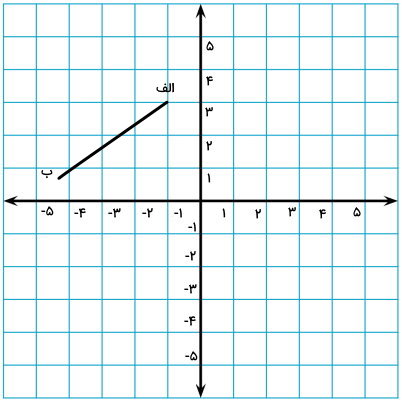
به منظور رسم قرینه خط الف ب، ابتدا نقاط ابتدایی و انتهایی آن را علامت می‌زنیم.

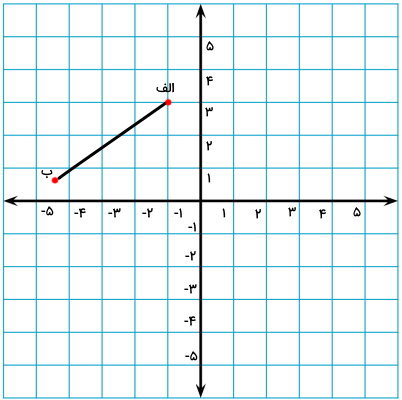
سپس، فاصله نقطه ابتدایی خط (نقطه الف) را نسبت به محور افقی مختصات به دست می‌آوریم.

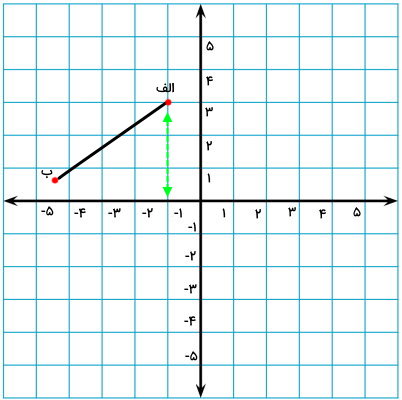
با استفاده از این فاصله، موقعیت قرینه نقطه الف در طرف مقابل محور افقی را تعیین می‌کنیم.

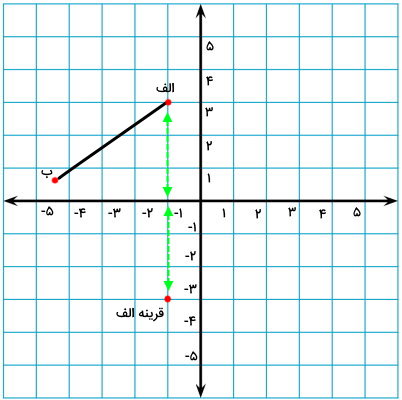
به همین شکل، موقعیت قرینه نقطه انتهایی خط (نقطه ب) را نیز به دست می‌آوریم.

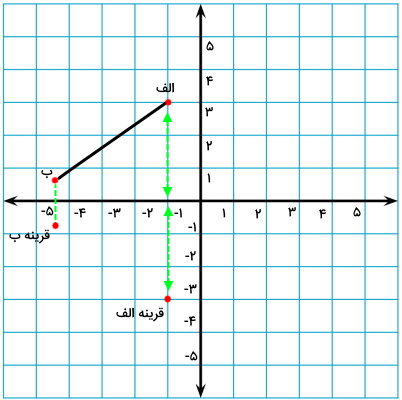
اکنون، نقطه ابتدایی و انتهایی قرینه خط را داریم. کافی است این دو نقطه را به یکدیگر وصل کنیم تا قرینه خط به دست بیاید.

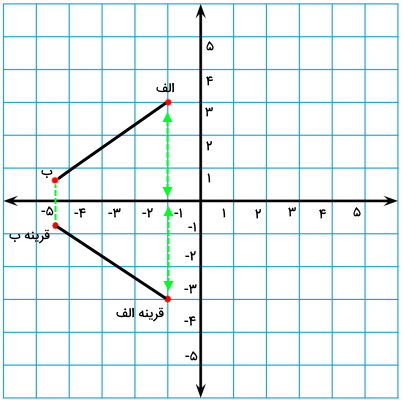
تصویر زیر، قرینه خط الف ب نسبت به محور افقی مختصات را نمایش می‌دهد.

مثال 2: رسم قرینه نسبت به خط تقارن عمودی

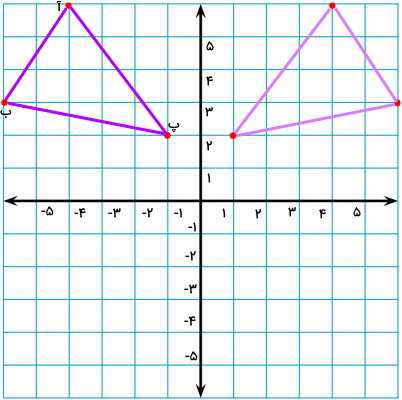
قرینه مثلث «آ ب پ» را نسبت به محور عمودی پیدا کنید.

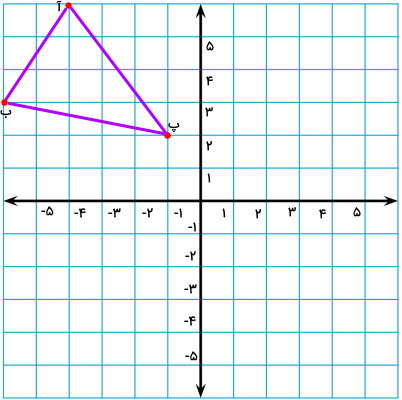
به منظور رسم قرینه مثلث، ابتدا قرینه گوشه‌های آن را پیدا می‌کنیم.

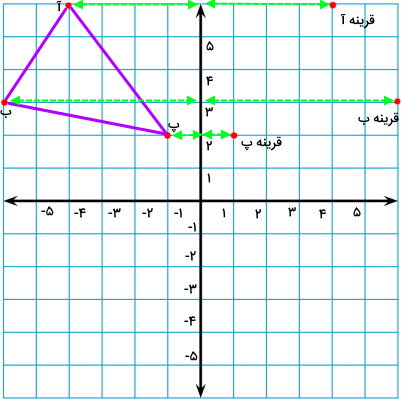
به این ترتیب، سه نقطه از قرینه مثلث به دست می‌آید. این نقاط، همان راس‌های قرینه مثلث هستند.

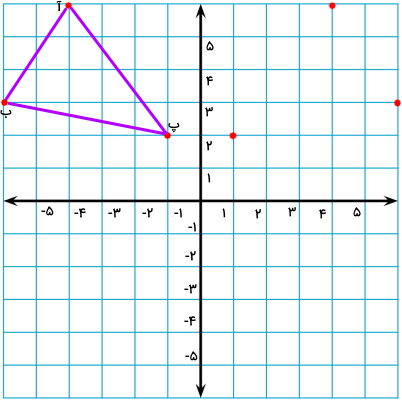
راس‌های به دست آمده را به یکدیگر وصل می‌کنیم.

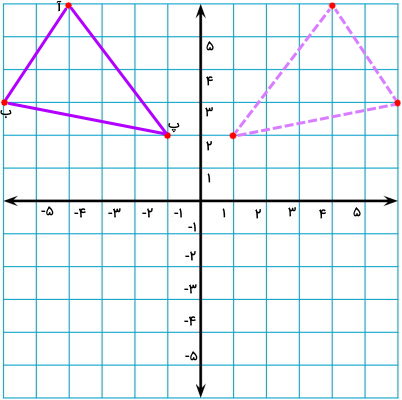
در نهایت، قرینه شکل مثلث به وجود می‌آید.

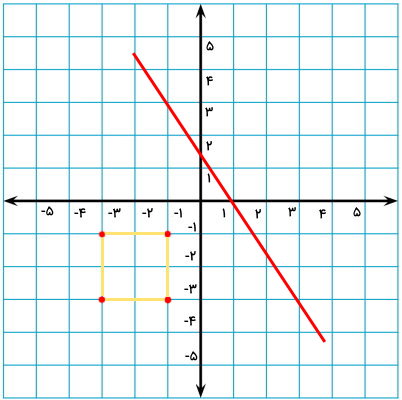
مثال 3: رسم قرینه نسبت به خط مورب

قرینه مربع را نسبت به خط مورب پیدا کنید.

برای این‌که بتوانیم قرینه شکل را نسبت به یک خط مورب رسم کنیم، ابتدا باید فاصله عمودی نقاط معرف شکل را تا آن خط به دست بیاوریم. بهترین ابزار برای پیدا کردن قرینه شکل در این شرایط، گونیا است. با استفاده از خط‌کش گونیا، فاصله هر نقطه تا خط مورب را تعیین می‌کنیم. ساق‌های گونیا، به منظور اطمینان از عمود بودن این فاصله به کار می‌روند. در قدم بعدی، موقعیت قرینه نقاط معرف شکل را در طرف دیگر خط علامت می‌زنیم. به عنوان مثال، یکی از گوشه‌های مربع را در نظر بگیرید. فاصله این گوشه تا خط مورب به صورت زیر به دست می‌آید.

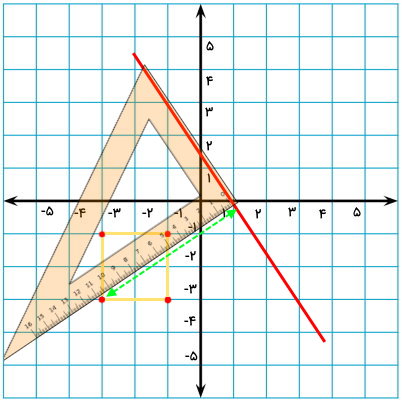
در تصویر بالا، فاصله عمودی نقطه نمایش داده شده تا خط مورب برابر با 11 سانتی‌متر است. گونیا را در همین راستا و در طرف مقابل خط تنظیم می‌کنیم. سپس، کنار اندازه 11 سانتی‌متر، علامت می‌زنیم. این علامت، قرینه یکی از گوشه‌های مربع است.

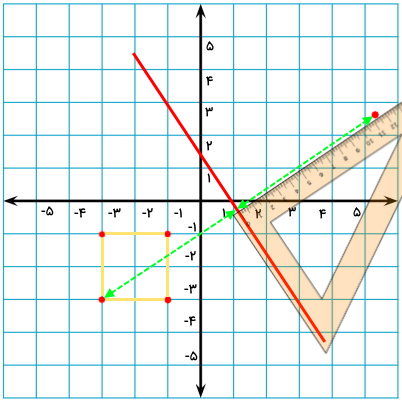
به همین شکل، موقعیت قرینه نقاط دیگر را نیز به دست می‌آوریم.

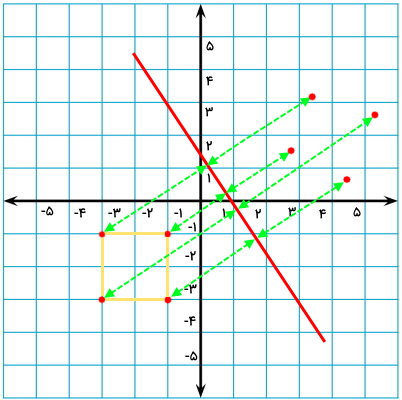
اکنون، چهار نقطه در طرف مقابل خط مورب داریم که هر یک، یکی از گوشه‌های قرینه مربع را نمایش می‌دهند.

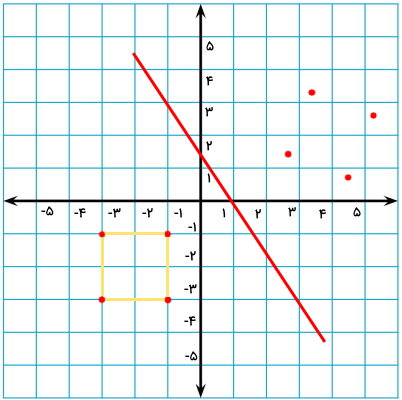
نقاط قرینه را به یکدیگر وصل می‌کنیم. به این ترتیب، قرینه شکل مربع به دست می‌آید.

مثال 4: رسم قرینه نسبت به نقطه

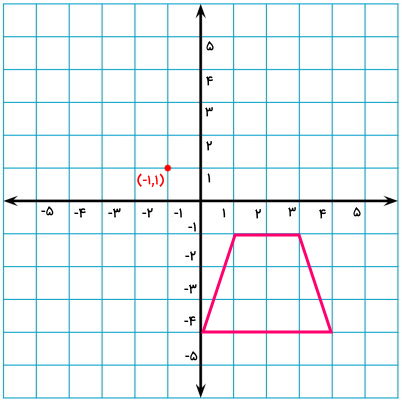
قرینه ذوزنقه را نسبت به نقطه (1,1-) پیدا کنید.

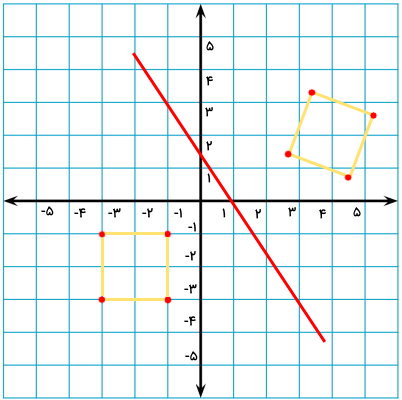
به منظور رسم قرینه ذوزنقه بالا، ابتدا موقعیت نقطه (1,1-) را به عنوان نقطه تقارن مشخص می‌کنیم.

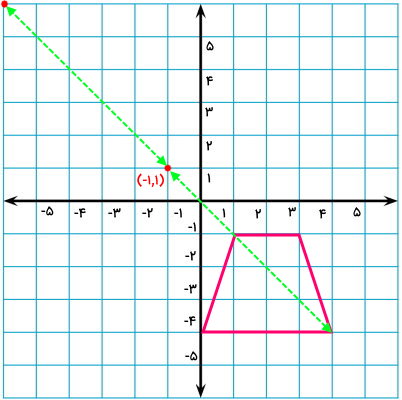
در قدم بعدی، اندازه فاصله یکی از گوشه‌های ذوزنقه تا نقطه تقارن را به دست می‌آوریم. سپس، با ادامه دادن راستای این فاصله به همان اندازه، موقعیت قرینه گوشه مورد نظر را مشخص می‌کنیم.

تعیین موقعیت قرینه را برای گوشه‌های دیگر نیز انجام می‌دهیم.

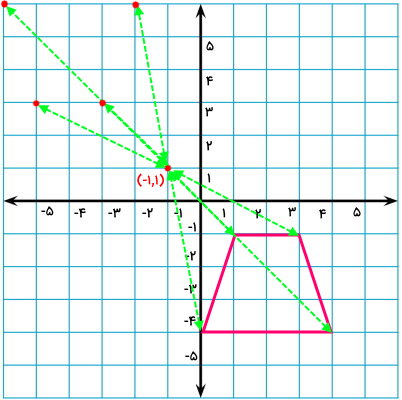
نقاط قرینه را به یکدیگر وصل می‌کنیم. به این ترتیب، قرینه شکل ذوزنقه نسبت به نقطه مورد نظر به دست می‌آید.

رسم قرینه شکل با استفاده از مختصات نقاط

در بخش قبلی، مثال‌های مختلفی از نحوه رسم قرینه شکل با استفاده از فاصله نقاط را مرور کردیم. روش‌های دیگری برای رسم قرینه اشکال هندسی وجود دارد. یکی از این روش‌ها، استفاده از قواعد تبدیل مختصات نقاط به قرینه آن‌ها است. در ادامه، مراحل انجام این روش را با حل چند مثال توضیح می‌دهیم.

مثال 5: رسم قرینه شکل لوزی با مختصات

قرینه لوزی زیر را نسبت به محور افقی دستگاه مختصات پیدا کنید. برای این کار، از مختصات نقاط لوزی کمک بگیرید.

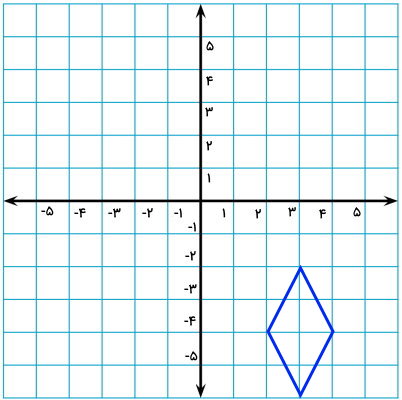
برای این‌که قرینه لوزی را نسبت به محور افقی رسم کنیم، ابتدا مختصات گوشه‌های آن را تعیین می‌کنیم. این مختصات در تصویر زیر نمایش داده شده‌اند.

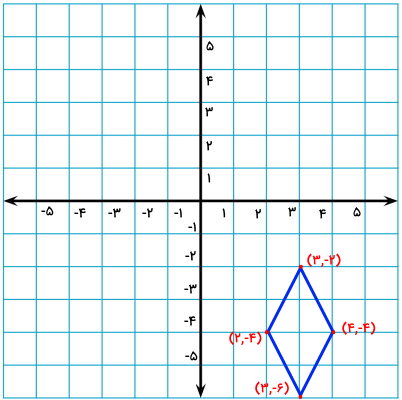
هنگام قرینه کردن یک شکل نسبت به محور افقی مختصات، ارتفاع (عدد دوم مختصات) منفی می‌شود. بنابراین، مختصات قرینه هر یک از گوشه‌های لوزی برابر است با:

• قرینه (2-,3) برابر با (۳,۲) است.
• قرینه (4-,4) برابر با (4,4) است.
• قرینه (6-,3) برابر با (3,6) است.
• قرینه (4-,2) برابر با (۲,4) است.

مختصات قرینه گوشه‌های لوزی را در دستگاه مختصات مشخص می‌کنیم.

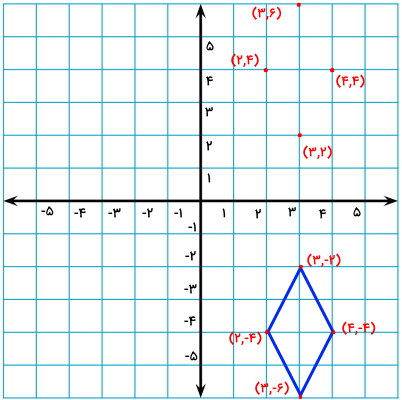
نقاط قرینه را به یکدیگر وصل می‌کنیم. به این ترتیب، قرینه لوزی به دست می‌آید.

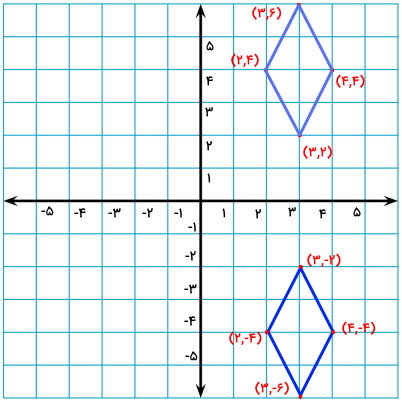
مثال 6: رسم قرینه نیم

قرینه شکل نیم‌دایره زیر را نسبت به محور عمودی مختصات رسم کنید.

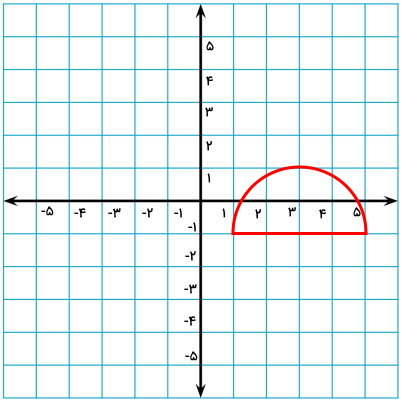
برای این‌که قرینه نیم‌دایره را بالا را به دست بیاوریم، مانند مثال قبلی، ابتدا مختصات برخی از نقاط آن را تعیین می‌کنیم.

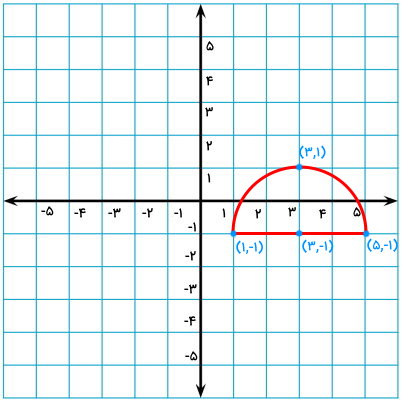
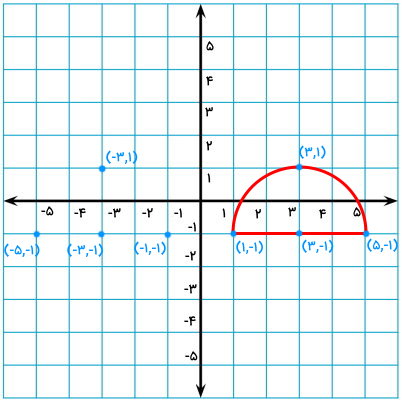
هنگام قرینه کردن یک شکل نسبت به محور عمودی مختصات، عرض (عدد اول مختصات) منفی می‌شود. بنابراین، مختصات قرینه هر یک نقاط مشخص شده در تصویر بالا برابر است با:

• قرینه (۳,۱) برابر با (۳,۱-) است.
• قرینه (۱-,۵) برابر با (۱-,۵-) است.
• قرینه (۱-,3) برابر با (۱-,۳-) است.
• قرینه (۱-,۱) برابر با (۱-,۱-) است.

قرینه نقاط را در دستگاه مختصات مشخص می‌کنیم.

اکنون، این نقاط را به طوری به یکدیگر وصل می‌کنیم که قرینه نیم‌دایره تشکیل شود.

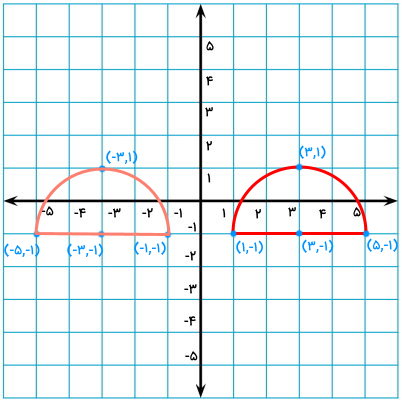
توجه داشته باشید که در رسم قرینه شکل‌های منحنی نظیر دایره، نیم‌دایره، بیضی و غیره، هر چه تعداد نقاط انتخابی بیشتر باشد، دقت رسم بالاتر می‌رود. در تصویر بالا، قرینه شکل را با استفاده از کامپیوتر رسم کرده‌ایم، به همین دلیل، این قرینه کاملا مشابه شکل اصلی شده است. در صورت استفاده از پرگار، دقت رسم دستی نیز بالا می‌رود.

مثال 7: رسم قرینه دایره

در تصویر زیر، شکل یک دایره و مختصات مرکز آن داده شده است. قرینه این دایره را نسبت به مرکز مختصات به دست بیاورید.

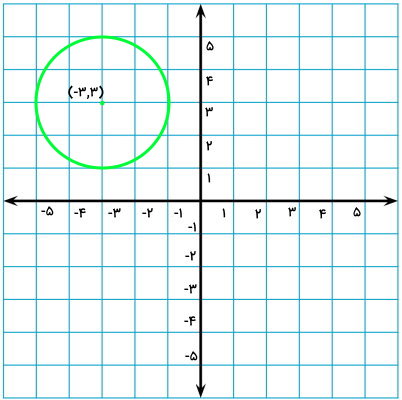
هنگام قرینه کردن یک شکل نسبت به مبدا مختصات، هر دو عدد مختصات تمام نقاط شکل منفی می‌شود. این موضوع برای مرکز دایره نیز صدق می‌کند. مختصات مرکز دایره بالا برابر با (۳,۳-) است. بنابراین، مختصات مرکز قرینه آن برابر با (۳-,۳) خواهد بود. این نقطه را در دستگاه مختصات مشخص می‌کنیم.

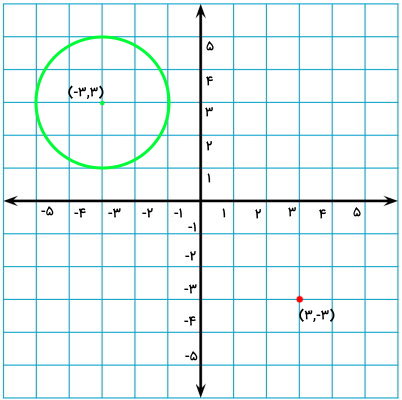
ساده‌ترین راه برای رسم قرینه دایره، استفاده از پرگار است. بر اساس تصویر بالا، شعاع دایره برابر با 2 واحد است. دهانه پرگار را به همین اندازه باز می‌کنیم و سوزن آن را بر روی مختصات مرکز قرینه دایره قرار می‌دهیم. سپس، یک دایره به شعاع 2 واحد رسم می‌کنیم. این دایره، قرینه شکل مورد نظر ما است.

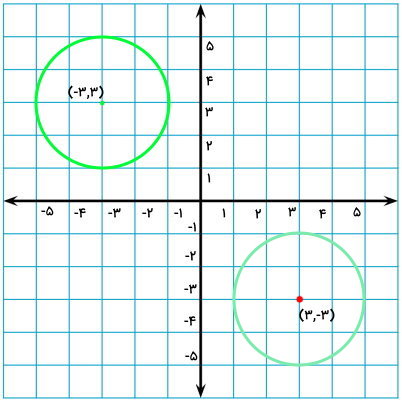
در صورت نداشتن پرگار، کافی بود مختصات چندین نقطه از دایره را به دست می‌آوردیم و اعداد آن‌ها را منفی می‌کردیم. به این ترتیب، چندین نقطه از شکل قرینه به دست می‌آمد. همان‌طور که در مثال قبل به آن اشاره کردیم، در این شرایط، هرچه تعداد نقاط انتخابی بیشتر باشد، دقت رسم قرینه نیز بیشتر می‌شود.

قرینه شکل و قرینه عدد

یکی از مفاهیم مشابه با مفهوم قرینه شکل در ریاضی، قرینه عدد است. قرینه هر عدد، به عنوان حاصلضرب آن عدد در (1-) شناخته می‌شود.

به عنوان مثال، محور اعداد زیر را در نظر بگیرید.

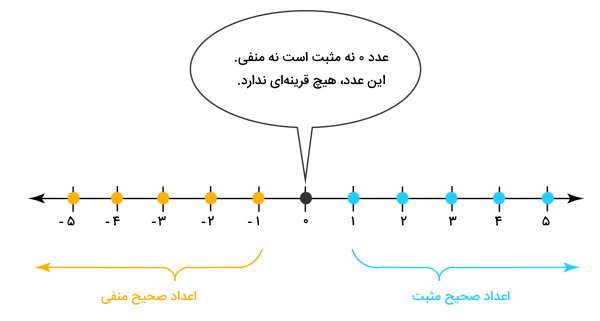
اعداد سمت راست عدد ۰، اعداد مثبت و اعداد سمت چپ عدد ۰، اعداد منفی محور اعداد هستند. در مجموعه اعداد صحیح، به ازای هر عدد مثبت، یک عدد منفی وجود دارد. این اعداد قرینه یکدیگرند. به عنوان مثال، عدد (۱-)، قرینه عدد (۱+) است.

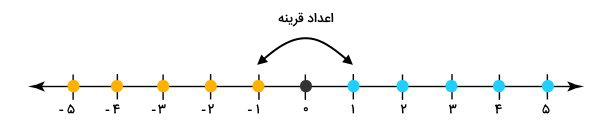
مبحث قرینه عدد را به طور مفصل در یک مطلب جداگانه مورد بررسی قرار خواهیم داد.

سوالات متداول در رابطه با قرینه شکل

در این بخش، به برخی از سوالات پرتکرار در رابطه با قرینه شکل های هندسی به صورت خلاصه پاسخ می‌دهیم.

قرینه یعنی چه ؟

قرینه به معنی بازتاب یک شکل نسبت به یک خط یا یک نقطه است.

وجود قرینه شکل نسبت به یک خط نشان دهنده چیست ؟

وجود قرینه شکل نسبت به یک خط نشان دهنده تقارن محوری یا بازتابی است.

وجود قرینه شکل نسبت به یک نقطه نشان دهنده چیست ؟

وجود قرینه شکل نسبت به یک خط نشان دهنده تقارن مرکزی است.

قرینه هر شکل چه رابطه ای با آن شکل دارد ؟

قرینه یک شکل، دقیقا با آن شکل هم‌اندازه است.