فازور چیست؟ — به زبان ساده (+ دانلود فیلم آموزش رایگان)
در آموزشهای قبلی مجله فرادرس، درباره ترانسفورماتورها و کاربردهای آن بحث کردیم. در این آموزش قصد داریم مبحث فازور در مهندسی برق را مطرح کنیم.
تعریف دیاگرام فازور
دیاگرام فازور یک روش بصری برای مقایسه اندازه و رابطه جهتدار بین دو یا چند کمیت متناوب است.
دو شکل موج سینوسی با فرکانس برابر، ممکن است اختلاف فاز داشته باشند. این اختلاف فاز، نمایانگر اختلاف زاویهای بین دو شکل موج است. همچنین واژههای «تاخیر» (Lag) و «تقدم فاز» (Lead) و عبارتهای «همفاز» (In-Phase) و «غیر همفاز» (Out-Of-Phase) برای نشان دادن رابطه بین دو موج به کار میروند. شکل موج سینوسی در حالت کلی به صورت زیر نمایش داده میشود:
$$A_{(t)} =A_m sin (\omega t \pm \phi)$$
این عبارت، نشاندهنده شکل موج سینوسی در حوزه زمان است.
در برخی موارد، نمایش ریاضی شکل موج، امکان نمایش بصری اختلاف زاویهای یا فازور بین دو یا چند شکل موج را از بین میبرد. یک راه برای غلبه بر این مشکل، نمایش حوزه شکل موجهای سینوسی با استفاده از حوزه فازور و «دیاگرام فازور» (Phasor Diagram) است. در این روش از متد «بردار گردان» (Rotating Vector) استفاده میشود.
به طور خلاصه، بردار گردان یا «فازور» (Phasor)، یک خط جهتدار است که اندازه (مقدار پیک یا ماکزیمم) و جهت (فاز) بردار را نشان میدهد و در یک نقطه از زمان نگه داشته شده است. فازور یک بردار است که یک پیکان در نوک خود دارد و مقدار ماکزیمم آن را نشان میدهد. این بردار در حوزه زمان در حال چرخش است و میتواند نشاندهنده ولتاژ یا جریان باشد.
به طور کلی، فازورها بردارهایی هستند که یک نقطه ابتدایی دارند و به آن «نقطه مبدأ» (Point of Origin) گفته میشود. نقطه انتهایی فازور، نمایانگر مقدار متغیر است و در جهت خلاف حرکت عقربههای ساعت با سرعتی برابر با فرکانس زاویهای ($$\omega$$) فازور میچرخد. بنابراین به طور قراردادی فرض میشود که چرخش بردار در جهت خلاف عقربههای ساعت، فاز بردار را افزایش میدهد. گفته میشود که این چرخش، یک «چرخش مثبت» (Positive Rotation) است. به همین ترتیب، چرخش بردار در جهت عقربههای ساعت را «چرخش منفی» (Negative Rotation) مینامند. در شکل زیر دیاگرام فازور و نمایش لحظهای آن، نشان داده شده است:
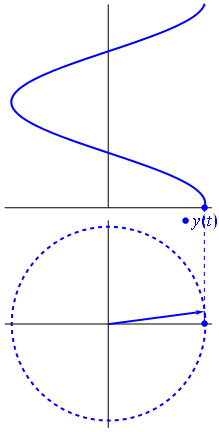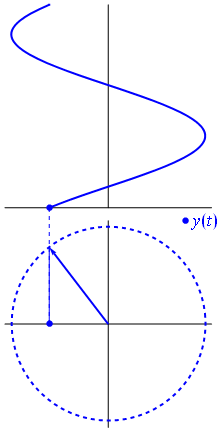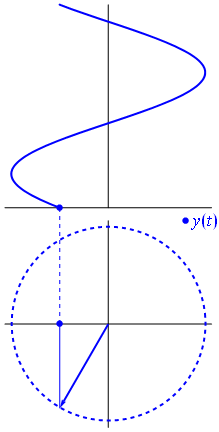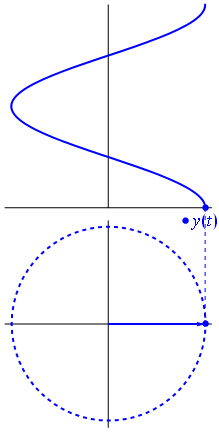
اگرچه هردو واژه بردار و فازور برای معرفی یک کمیت گردانِ دارای دامنه و جهت قابل استفاده است، اما تفاوت اصلی این دو واژه این است که دامنه بردار مقدار پیک یا ماکزیمم موج سینوسی را نشان میدهد، اما دامنه فازور مقدار rms موج سینوسی را نمایش میدهد. در هر دو حالت، زاویه فاز و جهت آن، یکسان است.
میتوان فاز یک کمیت متناوب در هر لحظه از زمان را با دیاگرام فاز نمایش داد. بنابراین دیاگرام فاز تابعی از زمان است. یک موج سینوسی کامل، یک بردار گردان با سرعت زاویهای $$\omega = 2 \pi f$$ است که در آن، $$f$$ فرکانس شکل موج است.
به طور کلی، سرعت زاویهای شکل موج سینوسی ($$\omega$$)، با واحد رادیان بر ثانیه تعریف میشود.
دیاگرام فازور در شکل زیر را در نظر بگیرید:

هنگامی که بردار تکی (مانند برق یک فاز)، خلاف جهت حرکت عقربههای ساعت میچرخد، رأس آن در نقطه A، به اندازه یک دوره تناوب کامل یا $$360 ^ \circ $$ یا $$2 \pi$$ دوران میکند. اگر طول پیکان متحرک در حوزه زمان رسم شود، یک شکل موج سینوسی به دست میآید. شروع این موج، از نقطه صفر یا مبدأ است. هر نقطه در محور افقی نمایانگر زمان گذشته از صفر یا $$t=0$$ است. قرارگیری بردار در حالت افقی، نمایانگر زوایای $$0^ \circ$$ و $$180^ \circ$$ و $$360^ \circ$$ است.
به همین ترتیب، بردار عمودی نشاندهنده مقدار پیک مثبت بردار ($$+A_m$$) در $$90^ \circ$$ یا $$\pi/2$$ یا مقدار پیک منفی بردار ($$-A_m$$) در $$3 \pi /2$$ است. محور زمان در شکل موج، زاویه را بر حسب درجه یا رادیان نشان میدهد. پس میتوان گفت فازور، یک بردار گردان از مقدار ولتاژ یا جریان است که در نقطهای از زمان مثل $$t$$ نگه داشته شده است. در مثال بالا، فازور $$A$$ در زاویه $$30 ^ \circ$$ نشان داده شده است.
هنگام تحلیل شکل موج متناوب لازم است محل فازور دانسته شود. یعنی نقطه دقیق فازور در زمان مشخص باشد تا بتوان دو شکل موج متفاوت ولتاژ یا جریان را مقایسه کرد.
فرض شده است که شکل موج از نقطه $$t=0$$ شروع میشود و زاویه فاز مرتبط با آن، واحد درجه یا رادیان دارد.
اما اگر یک شکل موج دوم در سمت راست یا چپ نقطه صفر داشته باشیم یا بخواهیم در حوزه فازور به بررسی رابطه بین دو شکل موج بپردازیم، لازم است اختلاف فاز بین دو شکل موج ($$\phi$$) محاسبه شود. فرض کنید اختلاف فاز دو شکل موج سینوسی به صورت زیر باشد:

عبارت عمومی ریاضی برای تعریف این دو کمیت سینوسی به صورت زیر نوشته میشود:
$$V_{(t)} = V_m sin(\omega t)$$
$$i_{(t)} = I_m sin(\omega t - \phi)$$
جریان $$i$$، نسبت به ولتاژ $$v$$، به اندازه زاویه $$\phi$$ تأخیر دارد. در این مثال، این اختلاف فاز برابر با $$30 ^ \circ$$ است. اختلاف بین دو فازور که نشاندهنده دو کمیت سینوسی هستند، با زاویه $$\phi$$ نشان داده میشود. این دو موج سینوسی در شکل زیر نشان داده شدهاند:
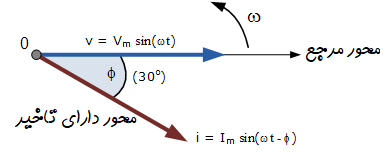
دیاگرام فازور نشان داده شده مربوط به زمان صفر ($$t=0$$) روی محور افقی است. طول فازورها متناسب با مقدار ولتاژ (V) و جریان (I) در لحظه صفر است. گفته میشود که فازور جریان نسبت به فازور ولتاژ به اندازه زاویه $$\phi$$ تاخیر دارد. دو فازور در جهت خلاف حرکت عقربههای ساعت دوران میکنند. پس زاویه $$\phi$$ نیز در خلاف جهت عقربههای ساعت اندازهگیری میشود.
اگر دو موج را در زمان $$t=30^ \circ$$ نگه داریم، دیاگرام فازور مربوطه مانند شکل زیر خواهد شد:
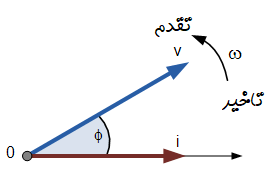
بار دیگر مشاهده میشود که فازور جریان نسبت به فازور ولتاژ تاخیر دارد، زیرا دو شکل موج فرکانس یکسانی دارند.
در لحظهای که شکل موج جریان در محور افقی از نقطه صفر عبور میکند، میتوان این لحظه از زمان را به عنوان مرجع جدید فازور جریان در نظر گرفت. بنابراین میتوان گفت که فازور ولتاژ نسبت به فازور جریان به اندازه زاویه $$\phi$$، «تقدم» (Lead) دارد. در هر حال، یک فازور به عنوان «فازور مرجع» (Reference Phasor) در نظر گرفته میشود و بقیه فازورها نسبت به این مرجع، تقدم یا تاخیر دارند.
جمع دو فازور
در برخی موارد (مثلا در مدارهای سری AC، که مولفهها با یکدیگر همفاز نیستند)، لازم است دو شکل موج متناوب سینوسی با یکدیگر جمع شود. اگر مولفهها همفاز باشند (یعنی هیچ اختلاف فازی بین دو کمیت وجود نداشته باشد)، میتوان مثل حالت DC، دو بردار را به صورت جبری جمع کرد. برای مثال، اگر دو ولتاژ ۵۰ ولت و ۲۵ ولت با یکدیگر، همفاز باشند، برآیند این دو بردار، برابر ۷۵ ولت خواهد شد.
اگر دو موج همفاز نباشند (یعنی بردارهای آنها جهت یا نقاط شروع متفاوتی داشته باشد)، باید هنگام جمع دو فازور زاویه بین آن دو را در نظر گرفت. فازور منتجه یا بردار برآیند، با استفاده از «قانون متوازیالاضلاع» (Parallelogram Law) محاسبه میشود. شکل زیر، دو شکل موج AC را نشان میدهد:
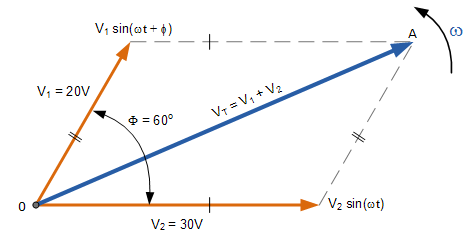
در این شکل دو فازور یکی $$V_1$$ با اندازه ماکزیمم ۲۰ ولت و دیگری $$V_2$$ با اندازه ماکزیمم ۳۰ ولت نشان داده شده است. فرض میشود که فاز $$V_1$$ از $$V_2$$ به اندازه $$60 ^ \circ$$ تقدم دارد. ولتاژ کلی ($$V_T$$) را میتوان با رسم دیاگرام فازور و سپس رسم متوازیالاضلاع محاسبه کرد. دو ضلع این متوازیالاضلاع، ولتاژهای $$V_1$$ و $$V_۲$$ هستند.
به این ترتیب، مجموع دو فازور به آسانی با اندازهگیری طول قطر متوازیالاضلاع محاسبه میشود. به این قطر، «بردار برآیند» (Resultant Vector) نیز گفته میشود. نقطه ضعف این روش این است که رسم دو فازور و مقیاسبندی آنها زمانبر است. شکل زیر، دیاگرام برآیند دو فازور و نمایش لحظهای برآیند را نشان میدهد:
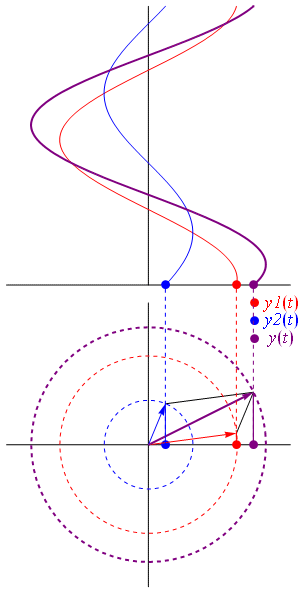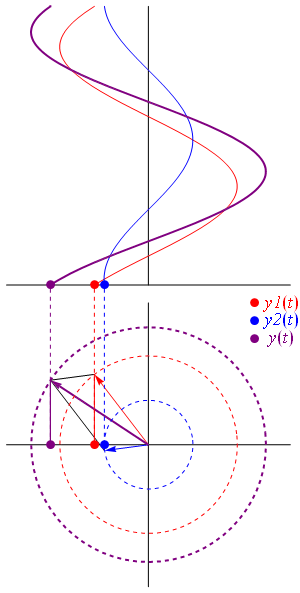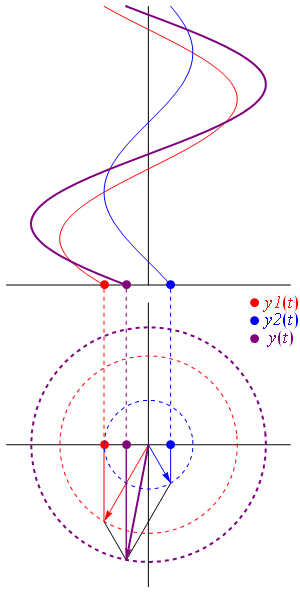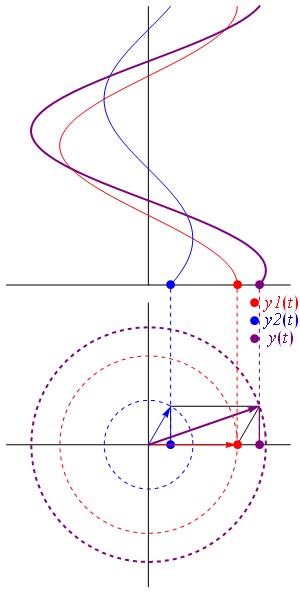
جمع دو بردار به روش مستطیلی
اگرچه این روش گرافیکی، برای بیشتر کاربردها جوابی تقریبا با دقت به دست میدهد، اما اگر با دقت کشیده نشود یا به درستی مقیاسبندی نشود، ممکن است منبع تولید خطا شود. یک راه برای تضمین صحت جواب، استفاده از روشهای تحلیلی است.
از ریاضیات میدانیم که هر بردار را میتوان به دو مولفه افقی و عمودی خود تبدیل کرد. برای جمع دو بردار نیز میتوان از این روش استفاده کرد. برای جمع دو بردار، ابتدا مولفههای افقی و عمودی آن دو را جمع میکنیم. جمع مولفه افقی و عمودی بردار منتجه، برآیند دو بردار اولیه را نشان میدهد. این روش تحلیلی که از قانون سینوس و کسینوس برای یافتن مقدار برآیند استفاده میکند، «فرم مستطیلی» (Rectangular Form) برآیند دو بردار نام دارد.
در فرم مستطیلی، فازور به یک قسمت حقیقی (x) و یک قسمت موهومی (y) تبدیل میشود. بنابراین فرم کلی فازور، عبارت $$Z=x \pm jy$$ خواهد بود. اندازه و فاز ولتاژ سینوسی به صورت زیر تعریف میشود:
$$V_m = cos (\phi) + j V_m (sin \phi)$$
پس جمع دو بردار $$A$$ و $$B$$ بر اساس عبارات قبلی به صورت زیر خواهد بود:
$$A= x +jy \, \, \, , \, \, \,B=w+jz$$
$$A+B = (x+w) + j(y+z)$$
ولتاژ $$V_2$$ با اندازه ۳۰ ولت را در نظر بگیرید. فرض کنید که این بردار روی محور افقی قرار دارد. پس این بردار یک مولفه افقی دارد و مولفه عمودی ندارد. پس:
مولفه افقی = $$30 cos 0^ \circ$$ = 30 ولت
مولفه عمودی = $$30 sin 0 ^ \circ$$ = 0 ولت
حال ولتاژ $$V_1$$ با اندازه ۲۰ ولت را در نظر بگیرید. فازور $$V_1$$ نسبت به فازور $$V_2$$ به اندازه $$60^ \circ$$ تقدم دارد. پس هر دو مولفه افقی و عمودی را داراست که به صورت زیر هستند:
مولفه افقی = $$20 cos 60 ^ \circ$$ = $$20 \times 0.5$$ = 10 ولت
مولفه عمودی = $$20 sin 60 ^ \circ$$ = $$20 \times 0.866$$ = 17.32 ولت
بنابراین فرم مستطیلی برای ولتاژ $$V_1$$ به صورت زیر است:
$$V_1 = 10 + 17.32 j$$
برای به دست آوردن برآیند این دو ولتاژ مولفههای عمودی و افقی دو بردار $$V_1$$ و $$V_2$$ را با یکدیگر جمع میکنیم. مانند حالت زیر:
مولفه افقی بردار برآیند = جمع قسمت حقیقی دو بردار = ۱0+۳0 = 40 ولت
مولفه عمودی بردار برآیند = جمع قسمتهای موهومی دو بردار = 0 + 17.32 = 17.32 ولت
قسمتهای حقیقی و موهومی بردار برآیند محاسبه شده است. پس میتوان مقدار بردار برآیند را با استفاده از قضیه فیثاغورس برای مثلث قائم الزاویه، بردار برآیند دو فازور را نوشت:
$$V_T =\sqrt {40^2 + 17.32 ^ 2} \to V_T = 43.6 v $$
میتوان بردار برآیند با استفاده دیاگرام فازور به صورت زیر نیز رسم کرد:
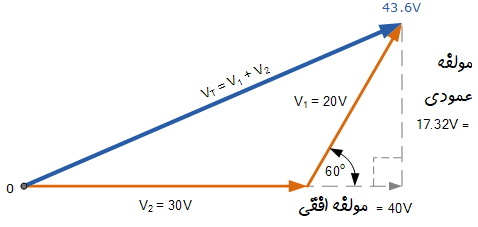
تفریق برداری دو فازور
تفریق دو فازور بسیار شبیه به روش مستطیلی است با این تفاوت که اختلاف دو بردار، قطر دیگر متوازیالاضلاع به دست آمده از دو بردار $$V_1$$ و $$V_2$$ است که در شکل زیر نشان داده شده است:
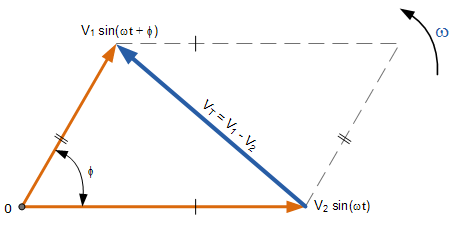
اگر دو بردار را به فرم فازوری آن نمایش دهیم، خواهیم داشت:
$$A = x + jy \, \, \, , \, \, \, B = w+jz $$
$$A-B = (x-w) + j(y-z) $$
دیاگرام فازور سه فاز
در مثالهای قبل، تنها به شکل موجهای تک فاز AC اشاره شد. به عنوان مثالی از موج تک فاز میتوان یک سیمپیچ چرخان در میدان مغناطیسی را در نظر گرفت. اما اگر سه سیمپیچ مشابه در نظر گرفته شود که هر کدام تعداد برابر دور دارند و در زوایای الکتریکی ۱۲۰ درجه نسبت به هم روی شفت یک روتور قرار گرفتهاند، یک ولتاژ سه فاز ایجاد خواهد شد.
ولتاژ سه فاز متعادل از سه ولتاژ سینوسی تشکیل شده است که همه آنها اندازه و فرکانس برابر دارند اما غیر همفاز هستند و دقیقا به اندازه ۱۲۰ درجه اختلاف فاز دارند.
سه بردار با رنگهای قرمز، زرد و آبی را برای نشان دادن فاز هر یک از بردارها در نظر میگیریم. بردار قرمز رنگ به عنوان فاز مرجع فرض میشود. مانند فازورهای تک فاز اشاره شده در بالا، فازور سه فاز نیز چرخشی در جهت خلاف عقربههای ساعت نسبت به نقطه مبدأ دارد که با نماد $$\omega$$ با واحد رادیان بر ثانیه نشان داده میشود. فازورها برای یک سیستم متصل متعادل ستاره یا مثلث به صورت زیر نشان داده میشود:
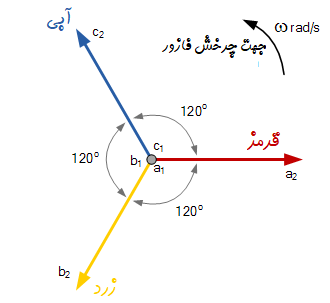
ولتاژ این سه فاز همگی مقداری برابر دارند اما زاویه فاز آنها متفاوت است. سه سیمپیچ به به یکدیگر در نقاط $$a_1$$ و $$b_1$$ و $$c_1$$ متصل شدهاند. این نقطه به عنوان زمین خنثی در نظر گرفته میشود. اگر فازور قرمز رنگ را به عنوان مرجع فاز در نظر بگیریم، هر کدام از فازورها بر اساس نقطه مشترک زمین تعریف میشود.
اگر فازور قرمز ($$V_{RN}$$) را به عنوان ولتاژ مرجع در نظر بگیریم، میتوان گفت فازور زرد ($$V_{YN}$$) به اندازه ۱۲۰ درجه از $$V_{RN}$$ تاخیر دارد. به همین ترتیب، فازور آبی ($$V_{BN}$$) از فازور زرد رنگ، به اندازه ۱۲۰ درجه تاخیر دارد. همچنین میتوان گفت که $$V_{BN}$$ نسبت به فازور قرمز رنگ ($$V_{RN}$$) به اندازه ۱۲۰ درجه تقدم دارد.
بنابراین میتوان معادلات ولتاژ سه فاز را صورت زیر نوشت:
فازور قرمز : $$V_{RN}$$ = $$V_m sin \theta$$
فازور زرد : $$V_{YN}$$ = $$V_m sin (\theta - 120 ^ \circ) $$
فازور آبی : $$V_{BN} = V_m sin (\theta - 240 ^ \circ) = V_m sin (\theta + 120^ \circ)$$
از آنجا که سه فازور نسبت به هم به اندازه ۱۲۰ درجه اختلاف دارند، میتوان گفت دیاگرام فازور شکل بالا، متعادل است. در یک سیستم سه فاز متعادل، جمع فازورها برابر صفر است. یعنی:
$$V_a + V_b + V_c =0$$
جمعبندی دیاگرام فازور
به طور خلاصه میتوان گفت که فازور برای نشان دادن مقدار لحظهای سیگنال به کار میرود. دیاگرام فازور میتواند نمایانگر هر لحظهای از زمان و هر زاویهای باشد. فازور مرجع برای یک کمیت متناوب، همواره در جهت مثبت محور $$x$$ رسم میشود.
- بردارها، فازورها و دیاگرامهای فازور همواره در مورد کمیتهای متناوب AC سینوسی صحیح هستند.
- دیاگرام فازور را میتوان برای نمایش هر تعداد کمیت سینوسی در هر لحظه از زمان به کار برد.
- در حالت کلی، فازور مرجع در جهت محور افقی قرار دارد. بقیه فازورها نسبت به این لحظه زمان رسم میشوند. همه فازورها، باید نسبت به مرجع محور افقی رسم شود.
- از دیاگرام فازور میتوان برای نمایش بیش از دو موج سینوسی بهره برد. این امواج میتواند ولتاژ، جریان یا هر کمیت متناوب دیگری باشد. اما فرکانس همه آنها باید یکسان باشد.
- جهت چرخش همه فازورها در خلاف جهت حرکت عقربههای ساعت است. هر فازور که نسبت به فازور مرجع جلوتر باشد، تقدم فاز و هر فازور که نسبت به فازور مرجع عقبتر باشد، تاخر فاز دارد.
- به طور کلی، طول فازور نشاندهنده مقدار ماکزیمم کمیت سینوسی نیست بلکه مقدار rms کمیت را نشان میدهد.
- امواج سینوسی با فرکانسهای متفاوت را نمیتوان روی یک دیاگرام فازور نمایش داد زیرا سرعت حرکت بردارها متفاوت است. در هر لحظه از زمان زاویه فاز بین آنها متفاوت خواهد بود.
- دو بردار را میتوان با هم جمع یا از هم کم کرد. بردار منتجه در این حالت، بردار برآیند نام دارد.
- مولفه افقی یک بردار، قسمت حقیقی یا x بردار نام دارد. مولفه عمودی بردار، قسمت موهومی یا y بردار نام دارد. از قسمت حقیقی و قسمت موهومی بردار یک مثلث قائم الزاویه تشکیل میشود. وتر این مثلث، بردار برآیند این دو بردار متعامد است.
- در یک سیستم سه فاز متعادل، هر فازور با فازور مجاور خود به اندازه ۱۲۰ درجه اختلاف فاز دارد.
^^










با سلام و وقت بخیر
نمودار یک سینوسی وقتی فاز متغیر با زمان باشد به چه صورت خواهد بود؟
ممنون از پاسخگویی
سپاس ممنون از شما
سلام اون قسمت اول که درباره پیک صحبت شده پیک Am بجای منفی دوباره مثبت هست … لطفا اصلاح کنید ممنون
سلام.
متن بازبینی و اصلاح شد.
سپاس از همراهی و بازخوردتان.
عالی بود