شبیه سازی دینامیک مولکولی – به زبان ساده

دینامیک مولکولی (MD)، روشی برای آنالیز حرکت فیزیکی اتم‌ها و مولکول‌ها است. به اتم‌ها و مولکول‌ها در مدت زمان مشخصی فرصت داده می‌شود تا با یکدیگر برهم‌کنش انجام دهند تا از طریق آن، دیدگاهی در خصوص تکامل دینامیکی سیستم بدست آید. خط سیر اتم‌ها و مولکول‌ها را به کمک حل عددی معادله حرکت نیوتون تعیین می‌کنند. از آن‌جایی که یک سیستم مولکولی به طور معمول شامل تعداد اجزای بسیار زیادی است، به طور تحلیلی نمی‌توان خواص چنین سیستم‌های پیچیده‌ای را تعیین کرد. به همین دلیل، از روش‌های عددی کمک می‌گیرند. در این آموزش، موارد مقدماتی را جهت آشنایی با دینامیک مولکولی به زبان ساده بررسی می‌کنیم.

مقدمه

اساس نظری برای دینامیک مولکولی، شامل بررسی دیدگاه‌های بسیاری از دانشمندان در خصوص مکانیک تحلیلی از جمله اویلر،‌ همیلتون، لاگرانژ و نیوتون است. ساده‌ترین شکل دینامیک مولکولی، چیزی بیشتر از قانون دوم نیوتون را در بر دارد. درحالیکه شبیه‌سازی دینامیک مولکولی به شدت به کامپیوترها وابسته است اما نگاهی هم به توسعه دو موضوع فیزیک یعنی نسبیت و مکانیک کوانتوم دارد.

فیلم آموزش ترمودینامیک مهندسی شیمی – جامع و کاربردی در فرادرس

کلیک کنید

نسبیت خاص، انتقال اطلاعات را در سرعت‌های بالاتر از نور شرح می‌دهد. مکانیک کوانتوم نیز، اصل عدم قطعیت را شامل می‌شود. در این بین، شبیه‌سازی دینامیک مولکولی، نیازمند اطلاعات کاملی در خصوص مکان و تکانه در هر لحظه است.

برهم‌کنش‌ها و معادله حرکت

ابتدایی‌ترین مدل میکروسکوپی برای مواد با سه حالت جامد، مایع و گاز، بر اساس برهم‌کنش ذرات کروی با یکدیگر بنا شده است. این برهم‌کنش‌ها در ساده‌ترین حالت خود، بین جفت‌های اتمی اتفاق می‌افتند که در نهایت، دو ویژگی اساسی را در نیروهای بین‌اتمی بوجود می‌آورند. اولین ویژگی، مقاومت در برابر متراکم شدن و دومین ویژگی، تشکیل پیوند بین اتم‌ها در حالت‌های مایع و جامد است. توابع پتانسیلی که این ویژگی‌ها را توصیف کنند، شکل‌های مختلفی خواهند داشت و اگر به دقت انتخاب شوند، مدل صحیحی از مواد را بدست می‌دهند.

از جمله بهترین مدل‌ها،‌ مدلی است که برای آرگون مایع موسوم به «لنارد جونز» (LJ) پیشنهاد شده است. انرژی پتانسیل در این رابطه برای یک جفت اتم $$i$$ و $$j$$، که در $$r_i$$ و $$r_j$$ قرار دارند به صورت زیر تعریف می‌شود:

$$\begin{equation}<br /> u\left( r _ { i j }\right) = \left\{\begin{array}{ll}<br /> {4 \epsilon\left[\left(\frac{\sigma}{r _ { i j}}\right) ^ {1 2 }-\left(\frac{\sigma}{r _ { i j}}\right) ^ { 6 }\right]} & {r_{i j}<r_{c}} \\<br /> {0} & {r _ {i j} \geq r_{c}}<br /> \end{array}\right.<br /> \end{equation}$$

در این رابطه:

• $$r _ { i j } = r_ i - r_ j$$
• $$r _ { i j } = |r _ { i j }|$$
• $$\epsilon$$: بیانگر قدرت برهم‌کنش
• $$\sigma$$: مقیاس طول

این برهم‌کنش‌ها در بازه‌های بسیار نزدیک، به صورت دافعه‌ هستند و بعد از آن به صورت جاذبه عمل می‌کنند که این جاذبه در نهایت، در $$r_c$$ از بین می‌رود. این برهم‌کنش‌ها شامل جفت‌های اتمی می‌شوند که هر جفت را به طور جداگانه مورد بررسی قرار می‌دهند به گونه‌ای که اتم‌ها موجود در همسایگی، هیچ اثری بر نیروهای بین آن‌ها ندارند. این رابطه را به صورت ساده شده زیر نیز نشان می‌دهند:

$$\begin{equation} u\left( r _ {i j }\right)=\left\{\begin{array}{ll} {4 \epsilon\left[\left(\frac{\sigma}{r _ {i j}}\right)^{1 2}-\left(\frac{\sigma}{r_{i j}}\right)^{6}\right]+\epsilon} & { r _ { i j} < r _ {c } = 2 ^ { 1 / 6} \sigma} \\ {0} & {r _ {i j} \geq r _ { c}} \end{array}\right. \end{equation}$$

مدلی که از طریق این رابطه بدست می‌آید، قدری پیچیده‌تر از تجمع ذرات توپی‌شکل و نرم و برخورد آن‌ها است. نیروی متناظر با $$u ( r )$$ عبارتست از:

$$\begin{equation} f = - \nabla u ( r) \end{equation}$$

بنابراین،‌ نیرویی که اتم $$j$$ بر اتم $$i$$ وارد می‌کند برابر است با:

$$\begin{equation} f _ { i j } = \left(\frac{ 4 8 \epsilon}{\sigma ^ { 2 }}\right)\left[\left(\frac{\sigma}{r _ {i j}}\right) ^ {1 4 } - \frac{ 1}{ 2}\left(\frac{\sigma}{ r _ { i j}}\right) ^ {8}\right] r _ { i j} \end{equation}$$

مقدار عبارت بالا برای مقادیر $$r _ {ij} < r _ c$$ و در غیر از این حالت، برابر با صفر است. هرقدر میزان $$r$$ به $$r_c$$ نزدیک‌تر (بزرگتر) شود،‌ نیرو به صفر نزدیک می‌شود. بنابراین هیج ناپیوستگی در $$r_c$$ برای نیرو و پتانسیل دیده نمی‌شود. معادله حرکت در قانون دوم نیوتون،‌ به صورت رابطه زیر تعریف می‌شود:

$$\begin{equation} m \ddot{r}_{i}=f_{i}=\sum_{j=1 \atop j \neq i}^{N_{m}} f_{i j} \end{equation}$$

در این رابطه، $$m$$ جرم اتمی است. قانون سوم نیوتون نیز بیان می‌کند که $$f _ {ij} = - f _ {ji}$$، بنابراین، هر جفت‌ اتمی را تنها یک بار مورد بررسی قرار می‌دهیم. مقدار کار انجام شده نیز با $$N _ m ^ 2$$ متناسب است، در نتیجه، برای مدل‌هایی که در آن‌ها $$r_c$$ در مقایسه با اندازه ظرف، کوچک باشند، بهتر است که جفت‌های اتمی را برای $$r {i j } \leq r _ c$$ مشخص کنیم تا مقادیر محاسبات کاهش یابند.

واحدهای بدون بعد در دینامیک مولکولی

در ادامه قصد داریم تا برخی واحدهای بدون بعد در دینامیک مولکولی را بیان کنیم. دلایل مختلفی برای این کار وجود دارند که از آن‌جمله می‌توان به کار با مقادیر عددی اشاره کرد که به جای اینکه اعداد بسیار کوچکی باشند، مقادیری نزدیک به واحد دارند. از جمله مزایای دیگر واحدهای بدون بعد، این است که معادله حرکت نیز ساده خواهد شد. با بدون بعد کردن ابعاد و ساده شدن روابط، در حقیقت، یک مدل ساده می‌تواند مسائل مختلفی را توصیف کند و زمانی که خصوصیات، به صورت بدون بعد اندازه‌گیری شدند، به راحتی می‌توان آن‌ها را به مقیاس‌های مختلف تبدیل کرد.

در مطالعات دینامیک مولکولی با استفاده از مدل LJ، مناسب‌ترین واحدهای بدون بعد با انتخاب $$\sigma$$، $$m$$ و $$\epsilon$$ به ترتیب به صورت واحدهای طول، جرم و انرژی و به شکل زیر، تعریف می‌شوند:

• طول: $$r \rightarrow r \sigma$$
• انرژی: $$e \rightarrow e \epsilon$$
• زمان:‍ $$\begin{equation} t \rightarrow t \sqrt{m \sigma^{2} / \epsilon} \end{equation}$$

در نتیجه، شکل اصلی معادله حرکت به صورت واحدهای دینامیک مولکولی، به شکل زیر خواهد بود:

$$\begin{equation} \ddot{r}_{i}=48 \sum_{j(\neq i)}\left(r_{i j}^{-14}-\frac{1}{2} r_{i j}^{-8}\right) r_{i j} \end{equation}$$

 انرژی‌های جنبشی و پتانسیل نیز به ازای هر اتم، به شکل زیر تعریف می‌شوند:

$$\begin{equation}<br /> \begin{array}{l}<br /> {E_{K}=\frac{1}{2 N_{m}} \sum_{i=1}^{N_{m}} v_{i}^{2}} \\<br /> {E_{U}=\frac{4}{N_{m}} \sum_{1 \leq i<j \leq N_{m}}\left(r_{i j}^{-12}-r_{i j}^{-6}\right)}<br /> \end{array}<br /> \end{equation}$$

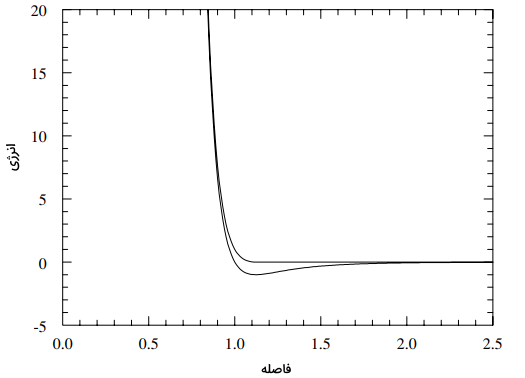
در رابطه بالا، $$v_i$$ را سرعت در نظر می‌گیرند. نمودار انرژی‌های برهم‌کنش LJ و «کره‌های نرم»‌ (Soft Sphere) در واحدهای دینامیک مولکولی بر حسب فاصله را در تصویر زیر مشاهده می‌کنید.

به همین صورت، دما در یک سیستم دو یا سه بعدی نیز با رابطه زیر تعریف می‌شود:

$$\begin{equation} T=\frac{1}{d N_{m}} \sum_{i} v_{i}^{2} \end{equation}$$

اگر مدل بمنظور شبیه‌سازی دینامیک مولکولی آرگون مایع در نظر گرفته شده باشد، ارتباط بین واحدهای بدون بعد دینامیک مولکولی و داده‌های فیزیکی واقعی به صورت زیر خواهد بود:

طول به صورت $$\sigma=3.4 \mathrm{A}$$ تعریف می‌شود.

واحدهای انرژی به صورت $$\epsilon / k_{B}=120 \mathrm{K}$$ خواهند بود به گونه‌ای که: $$\epsilon = 120 \times 1.3806 \times 10 ^ {-16} erg /atom$$

اگر $$m$$ را به صورت جرم اتم آرگون و برابر با مقدار $$m=39.95 \times 1.6747 \times 10^{-24} \mathrm{g}$$ در نظر بگیریم، واحد زمانی دینامیک مولکولی برابر خواهد بود با $$2.161 \times 10 ^ {-12} s$$. در نتیجه، اگر میزان «گام زمانی» (Timestep) را برابر با $$\Delta t = 0.005$$ در نظر بگیریم، این میزان متناظر با مقدار $$10 ^ {-14} s$$ خواهد بود.

در نهایت، اگر تعداد $$N_m$$ اتم، فضایی مکعبی با ضلع L را اشغال کنند، چگالی معمول در مایع و برابر با $$0.942 g/cm^ 3$$، بیان می‌کند که $$L=4.142 N_{m}^{1 / 3} \mathrm{A}$$

شرایط مرزی

سیستم‌های «محدود» (Finite) و «نامحدود» (Infinite) با یکدیگر بسیار متفاوت هستند و میزان بزرگی یک سیستم کوچک، برای بیان رفتار یک سیستم نامحدود، پاسخی یکتا ندارد. شبیه‌سازی برای محفظه‌ای صورت می‌گیرد که دیواره‌های آن در حکم مرزی سخت هستند که اتم‌ها برای خروج از محدوده شبیه‌سازی، به آن‌ها برخورد می‌کنند. در سیستم‌هایی با اندازه ماکروسکوپی، تنها کسر کوچکی از اتم‌ها به میزان کافی به دیواره‌ها نزدیک هستند تا انحراف از فضای قالب را تجربه کنند.

به طور مثال، سیستمی سه بعدی با چگالی مایع و $$N _ m = 10 ^ {21}$$ را در نظر بگیرید. از آن‌جایی که تعداد اتم‌های نزدیک دیواره، از مرتبه $$N _ m ^ {2/3}$$ است، مقدار آن‌ها برابر با $$10 ^ {14}$$ خواهد بود. اما به طور معمول، برای مقادیری از $$N_ m = 1000$$، در حدود 500 اتم به دیواره‌ها نزدیک هستند. به همین دلیل، تنها زمانی این شبیه‌سازی موفق خواهد بود که بخواهیم رفتار اتم‌ها را در نزدیکی دیواره بررسی کنیم.

می‌توانیم یک سیستم محدود اما فارغ از دیواره فیزیکی را با استفاده از «شرایط مرزی تناوبی» (Periodic Boundary Condition) ایجاد کنیم که آن را در تصویر زیر مشاهده می‌کنید. این شرایط مرزی تناوبی را می‌توان به صورت آرایه‌ای از نمونه‌های مشابه محدوده شبیه‌سازی معرفی کرد. این شرایط مرزی تناوبی، دو تاثیر دارد: اول این‌که اتمی که ناحیه شبیه‌سازی را ترک کند، به سرعت به ناحیه دیگر وارد می‌شود. دومین مورد این است که اتمی که در فاصله $$r_c$$ از مرز قرار دارد، با اتم‌ها در ناحیه مجاور برهم‌کنش انجام می‌دهد که به این حالت «اثر کمربندی» (Wraparound Effect) می‌گویند.

اثر «Wraparound» را باید در معادلات حرکت و محاسبات برهم‌کنش‌ها لحاظ کرد. بعد از انجام هر «گام محاسباتی» (Integration Step) باید مختصات به طور مجدد ارزیابی شوند و اگر اتمی به خارج از محدوده حرکت کرده باشد، مختصات آن به طور مجدد تنظیم شوند تا دوباره در محدوده قرار بگیرد. به طور مثال، اگر مختصات $$x$$ را طوری تنظیم کرده باشیم که بین $$- L _ x /2$$ و $$L _ x /2$$ قرار بگیرد - که در این جا $$L_x$$، اندازه محدوده در جهت $$x$$ است - تنظیمات را می‌توانیم به صورت زیر اعمال کنیم. در صورتیکه محدوده مورد نظر به صورت مستطیلی دو بعدی یا منشور در سه بعد باشد،‌ کار با مرزهای تناوبی بسیار ساده خواهد بود:

• اگر $$\begin{equation} r _ {i x} \geq L _ { x } / 2 \end{equation}$$، آن را با $$r _ {i x } - L_ x$$ جایگزین کنید.
• در غیر اینصورت، اگر $$\begin{equation} r _ {i x} < -L _ { x } / 2 \end{equation}$$، آن را با $$\begin{equation} r _ {i x} + L _ { x } \end{equation}$$ جایگزین کنید.

برای لحاظ کردن برهم‌کنش‌ها در محاسبات نیز، به طور مشابه، به صورت زیر عمل می‌کنیم:

• اگر $$\begin {equation} r _ { i j x } \geq L _ { x } / 2 \end {equation}$$، آن را با $$\begin {equation} r _ { i j x }- L _ { x } \end {equation}$$ جایگزین کنید.
• در غیر اینصورت،‌ اگر $$\begin{equation} r _ {i j x} < -L _ { x } / 2 \end{equation}$$،  آن‌را با $$\begin{equation} r _ {i j x} + L _ { x } \end{equation}$$ جایگزین کنید.

شرایط اولیه

برای این‌که دینامیک مولکولی عملکرد قابل قبولی داشته باشد باید بتواند بیانگر بخشی از حالت کل سیستم باشد. یکی از نتایج عجیب این شرط، این است که نتایج شبیه‌سازی با مدت زمان مناسب، نسبت به شرایط اولیه، حساسیت (وابستگی) ندارد. یک انتخاب ساده، شروع با اتم‌هایی است که در شبکه‌ای مکعبی یا مربعی قرار دارند. سرعت‌های اولیه نیز بر اساس دما به اتم‌ها اختصاص داده می‌شوند که این مقادیر دارای جهات مختلف و مقدار ثابت هستند. همچنین، مرکز جرم سیستم نیز باید به گونه‌ای باشد که هیچ «جریان کلی» (Overall Flow) نداشته باشیم.

روش انجام شبیه سازی دینامیک مولکولی

جمع‌زنی (انتگرال‌گیری) معادلات حرکت،‌ از روش‌های عددی ساده‌ای همچون «روش لیپفراگ» (Leapfrog Method) استفاده می‌کند. اگر اندازه هر گام زمانی را به صورت $$h = \Delta t$$ تعریف کنیم، فرمول انتگرال‌گیری که بر هر جزء از مختصات و سرعت‌های یک اتم بکار می‌بریم، به صورت زیر تعریف می‌شود:

فیلم آموزش نرم افزار VMD برای شبیه سازی دینامیک مولکولی در فرادرس

کلیک کنید

$$\begin{equation} \begin{aligned} v _ {i x}(t + h / 2) & = v _ { i x}( t - h / 2) + h a _ {i x}(t) \\ r _{ i x}(t + h) & = r _ {i x}( t) + h v _ {i x}( t + h / 2) \end{aligned} \end{equation}$$

از لیپفراگ به این منظور استفاده می‌شود چراکه مختصات و سرعت‌ها در زمان‌های مختلف، ارزشیابی می‌شوند. اگر در هر لحظه‌ای که مختصات ارزشیابی می‌شوند، تخمین سرعت متناظر با زمان باشد، از رابطه زیر کمک می‌گیریم:

$$\begin{equation} v _ {i x}(t) = v _ {i x}(t - h / 2 ) + ( h / 2 ) a _ {i x}(t) \end{equation}$$

خطاهای محلی در این روش نیز برای مختصات از مرتبه $$h^ 4$$ و برای سرعت‌ها از مرتبه $$h ^ 2$$ است. روش لیپفراگ را می‌توان به گونه‌ای فرمول‌بندی کرد که مختصات و سرعت‌ها را در یک لحظه ارزشیابی کنیم و نیازی به تنظیمات سرعت و استفاده از رابطه بالا نباشد. برای این کار، محاسبات به دو بخش تقسیم می‌شوند: قبل از محاسبات، برای آپدیت کردن مقادیر سرعت و مختصات، به ترتیب از گام‌های زمانی «نیمه» (Half Timestep) و «کامل» (Full Timestep) به کمک روابط زیر، استفاده می‌کنیم:

$$\begin{equation} \begin{aligned} v _ { i x }(t + h / 2) &= v _ { i x }(t) + ( h / 2) a _ { i x }( t)\\ r _ { i x }( t + h ) &= r _ { i x }( t)+ h v _ {i x}(t + h / 2) \end{aligned} \end{equation}$$

حال با استفاده از مختصات جدید،‌ آخرین مقادیر شتاب محاسبه خواهند شد و سرعت‌ها را می‌توان برای نیمه‌گام زمانی دوم آپدیت کرد:

$$\begin{equation} v _ {i x}(t +h ) = v _ {i x}(t + h / 2)+( h / 2) a _ {i x}(t +h ) \end{equation}$$

سنجش و ارزیابی

خواصی که در سیستم‌های در حال تعادل،‌ بیشتر در دسترس هستند را پیش‌تر در ترمودینامیک آموخته‌ایم. این خواص عبارتند از انرژی و فشار که هرکدام را جداگانه به کمک دما (T) و چگالی $$(\rho)$$ توصیف می‌کنند. اندازه‌گیری چنین خواصی در زمان شبیه سازی دینامیک مولکولی امری ساده است و ارتباطی بین ترمودینامیک، برای درک ساختار اتمی ماده و رفتار آن در سطح میکروسکوپی برقرار می‌کند. در هر صورت، این انرژی است که در شبیه‌ سازی دینامیک مولکولی ثابت می‌ماند و بنابراین،‌ نتایج ترمودینامیکی به جای دما (T) بر اساس دمای متوسط بیان می‌شوند. در این بخش، انرژی و فشار، مقادیر اندازه‌گیری شده هستند که فشار را بر اساس «رابطه ویریال» (Virial Expression) تعریف می‌کنیم:

$$\begin{equation} P V = N _ { m} T + \frac{1}{d}\left\langle\sum _ { i = 1} ^ { N _ {m}} r _ {i} \cdot f _ { i}\right\rangle \end{equation}$$

در حالت دو بعدی، مساحت را جایگزین حجم می‌کنیم. برای پتانسیل جفت، رابطه بالا را به صورت مجموع برهم‌کنش‌های جفت‌های اتمی می‌نویسیم:

$$\begin{equation}<br /> P V=N_{m} T+\frac{1}{d}\left\langle\sum_{i<j} \boldsymbol{r}_{i j} \cdot \boldsymbol{f}_{i j}\right\rangle<br /> \end{equation}$$

همچنین، رابطه مربوط به نیروها نیز به شکل زیر تغییر پیدا می‌کند:

$$\begin{equation}<br /> P V=\frac{1}{d}\left\langle\sum_{i} v_{i}^{2}+48 \sum_{i<j}\left(r_{i j}^{-12}-\frac{1}{2} r_{i j}^{-6}\right)\right\rangle<br /> \end{equation}$$

با وجود این‌که انرژی کل ثابت می‌ماند،‌ فارغ از خطاهای عددی،‌ مقادیر فشار و دما تغییر می‌کنند و مقادیر آن‌ها برای گام‌های زمانی باید متوسط‌گیری شوند. این عمل را به طور معمول به کمک نرم‌افزارها و برنامه‌نویسی انجام می‌دهند.

فیلم آموزش ویدیویی شبیه سازی دینامیک مولکولی با نرم‌افزار LAMMPS (لمپس)

همانطور که در بخش قبل نیز به آن اشاره شد، شبیه سازی دینامیک مولکولی را می‌توان به کمک نرم‌افزارها و با استفاده از سایر روش‌ها انجام داد. به همین منظور، فرادرس اقدام به انتشار دوره آموزش ویدیویی شبیه‌ سازی دینامیک مولکولی به کمک نرم‌افزار «LAMMPS» کرده است که از طریق این لینک می‌توانید به آن دسترسی پیدا کنید. لازم به ذکر است که این نرم‌افزار، از جمله نرم‌افزارهای متن‌باز به شمار می‌آید که می‌توان آن‌را به صورت موازی اجرا کرد و به کمک آن، مدل‌ساز‌های پلیمری، اتمی و ... قابل انجام است.

این دوره آموزشی شامل چهار درس است که در درس یکم، مفاهیم پایه همچون برهم‌کنش‌های بین مولکولی و انتگرال‌گیری زمانی و کمیت‌های ترمودینامیکی مورد بررسی قرار می‌گیرند. در درس دوم، در خصوص بسته نرم‌افزاری LAMMPS صحبت خواهد شد و نصب آن بر روی «اوبونتو» (Ubuntu) و ویندوز به طور کامل مورد بررسی قرار خواهد گرفت. درس سوم به ساختار کد ورودی و قالب‌بندی، تنظیمات و اجرای شبیه‌سازی اختصاص دارد. در درس چهارم، مباحث پیشرفته ازجمله ایجاد نانولوله‌های کربنی و گرافن و همچنین ایجاد کامپوزیت مورد بررسی قرار خواهند گرفت.

فیلم آموزش شبیه سازی دینامیک مولکولی با نرم افزار لمپس LAMMPS در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های نرم‌افزارهای مهندسی شیمی
• مجموعه آموزش‌های مهندسی شیمی
• آموزش داکینگ مولکولی (Molecular Docking) با نرم افزار AutoDock
• اصطلاحات کروماتوگرافی گازی — به زبان ساده
• شیمی فضایی — به زبان ساده

^^