فرادرسشار مغناطیسی — به زبان ساده
در راستای ارائه مفاهیم مرتبط با فیزیک الکتریسیته، در این مطلب قصد داریم تا در مورد شار مغناطیسی و چگالی شار مغناطیسی بحث کنیم. البته پیشنهاد می‌شود به منظور درک بهتر در ابتدا مطالب میدان‌های الکتریکی و مغناطیسی را مطالعه فرمایید.
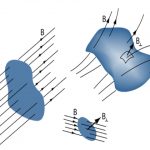
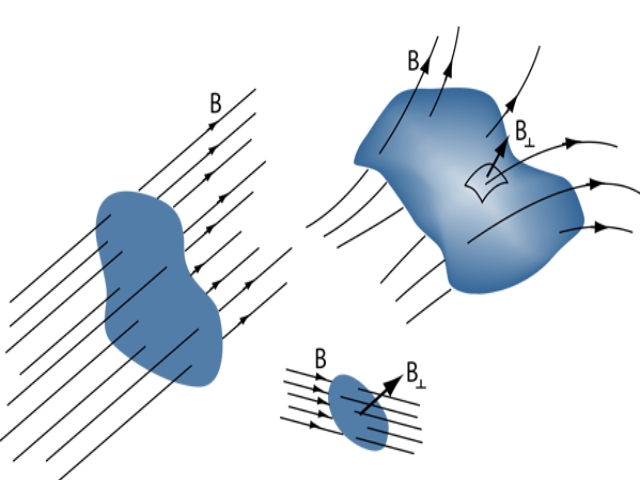
شار مغناطیسی
فضایی خالی را در نظر بگیرید که در آن میدان مغناطیسی وجود دارد. در این صورت عددی تحت عنوان چگالی شار مغناطیسیِ $$ B $$ را می‌توان مطابق با رابطه زیر تعریف کرد.
$$ B = µ _ 0 H $$
در رابطه فوق، $$ B $$ بر حسب وِبر بر متر به توان ۲ ($$ W b / m ^ 2 $$) یا در واحد‌های جدیدتر از تسلا ($$ T $$) یا گاوس ($$ G $$) استفاده می‌شود. رابطه بین این واحد‌ها نیز به شکل زیر است.
$$ 1 \ T = 1 \ W b / m ^ 2 = 10, 000 G $$
ثابت $$ \mu _ 0 $$، عددی بی‌بعد نبوده و مقداری مشخص را در خلاء دارد. واحد این عدد نیز هِنری بر متر ($$ H / m $$) بوده و مقدار آن نیز برابر است با:
$$ \mu _ { 0 } = 4 \pi \times 1 0 ^ { - 7 } \mathrm { H } / \mathrm { m } $$
مقدار $$ \mu _ 0 $$ تحت عنوان ضریب تراوایی مغناطیسی شناخته می‌شود. با توجه به این که $$ H $$ بر حسب آمپر بر متر انداز‌ه‌گیری می‌شود، بنابراین واحد وِبِر نیز برابر با حاصل‌ضرب هنری در آمپر است. چگالی شار مغناطیسیِ $$ B $$ مفهومی برداری محسوب می‌شود.
با استفاده از مفهوم چگالی شار مغناطیسی، شار مغناطیسی ($$ \Phi $$) را نیز می‌توان مطابق با رابطه زیر تعریف کرد:
$$ \Phi = \int _ { S } { B } \cdot d { S } \ \ \ \mathrm { W b } $$
توجه داشته باشید که $$ d S $$ نشان‌دهنده بردار دیفرانسیل سطح است. معادل شار مغناطیسی را می‌توان برای میدان الکتریکی و در قالب قانون گاوس نیز بیان کرد. در حقیقت برای شار الکتریکیِ $$ \Psi $$ می‌توان رابطه زیر را بیان کرد:
$$ \Psi = \oint _ { S } { D } \cdot d { S } = Q $$
در رابطه بالا $$ D $$ نشان‌دهنده چگالی شار الکتریکی است. همچنین $$ Q $$ مقدار بار الکتریکی قرار گرفته در سطح بسته $$ S $$ را نشان می‌دهد. همان‌طور که رابطه فوق نیز نشان می‌دهد می‌توان شار خالص الکتریکی را برای سطحی بسته تصور کرد. این در حالی است که تاکنون هیچ تک قطبی مغناطیسی در طبیعت یافت نشده؛ در نتیجه می‌توان گفت همواره حاصل انتگرال چگالی شار مغناطیسی روی یک سطح بسته برابر با صفر است. بنابراین می‌توان رابطه زیر را با اطمینان بیان کرد (با فرض این که تک قطبی مغناطیسی در طبیعت وجود نداشته باشد):
$$ \color {white} { { B } \cdot d { S } = 0 } \oint _ { S } { B } \cdot d { S } = 0 \color {white} { { B } \cdot d { S } = 0 } $$
با استفاده از قضیه دیورژانس، رابطه بالا را می‌توان به شکل زیر بازنویسی کرد:
$$ \color {white} {\cdot { B } = 0 } \nabla \cdot { B } = 0 \color {white} {\cdot { B } = 0 } $$
رابطه فوق در حقیقت آخرین معادله از چهارگانه معادلات ماکسول محسوب می‌شود. این معادلات به میدان‌های پایای مغناطیسی و الکتریکی اعمال می‌شود. در ادامه هر چهار معادله ارائه شده‌اند.
$$ \begin {align*} \nabla \cdot { D } & = \rho _ { v } \\ \nabla \times { E } & = 0 \\ \nabla \times { H } & = { J } \\ \nabla \cdot { B } & = 0 \end {align*} $$
با توجه به معادلات فوق می‌توان شکل انتگرالی آن‌ها را به صورت زیر نوشته و کرل و دیورژانس میدان‌های مغناطیسی و الکتریکی را مطابق با روابط زیر بیان کرد:
$$ \begin {array} { l } { \oint _ { S } { D } \cdot d { S } = Q= \int _ { \mathrm {vol} } \rho _ { v } d v } \\ { \oint { E } \cdot d { L } = 0 } \\ {\oint { H } \cdot d { L } = I = \int _ { S } { J } \cdot d { S } } \\ { \oint _ { S } { B } \cdot d { S } = 0 } \end {array} $$
برای درک بهتر فرض کنید می‌خواهیم شار و چگالی شار مغناطیسی را بین دو صفحه ارائه شده در شکل زیر بیابیم.
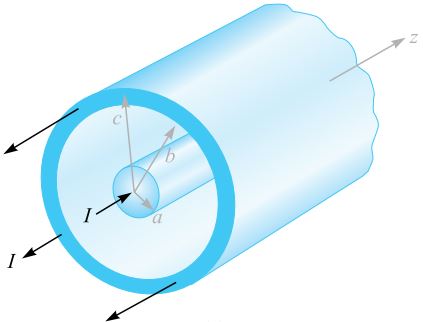
شدت میدان مغناطیسی برابر است با (این شدت در مبحثی مجزا محاسبه می‌شود):
$$ H _ { \phi } = \frac { I } { 2 \pi \rho } \quad ( a < \rho < b ) $$
در نتیجه چگالی شار مغناطیسی برابر است با:
$$ { B } = \mu _ { 0 } { H } = \frac { \mu _ { 0 } I } { 2 \pi \rho } { a } _ { \phi } $$
شار مغناطیسی قرار گرفته در طول $$ d $$ دو رسانا که در فاصله $$ ρ = a $$ و $$ ρ = b $$ وجود دارد را می‌توان با استفاده از انتگرال دوگانه زیر در فاصله $$ z = 0 $$ تا $$ z = d $$ بدست آورد.
$$ \Phi = \int _ { S } { B } \cdot d { S } = \int _ { 0 } ^ { d } \int _ { a } ^ { b } \frac { \mu _ { 0 } I } { 2 \pi \rho } { a } _ { \phi } \cdot d \rho d z { a } _ { \phi } $$
با محاسبه انتگرال فوق، عبارت زیر برای شار مغناطیسی بدست می‌‌آید.
$$ \color {white} {\Phi = \frac { \mu _ { 0 } I d } { 2 \pi } \ln \frac { b } { a } } \Phi = \frac { \mu _ { 0 } I d } { 2 \pi } \ln \frac { b } { a } \color {white} {\Phi = \frac { \mu _ { 0 } I d } { 2 \pi } \ln \frac { b } { a } } $$
از عبارت فوق می‌توان برای محاسبه اندوکتانس خط انتقال کواکسیالی استفاده کرد.
در صورتی که مطلب فوق برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
دوستان نور را اگر درست دقت کنید دارای جهت مغناطیسی است مثل اهنربا دارای یک قطب مثبت و یک قطب منفی است اگر درست نگاه کنید اگر یک نور را مثلا لیزر را به یک سطح استیل بتابانید مثل یک آهنربا می تواند در صفحه برو رود امواجش را می توان با چشم غیر مسلح دید یعنی می توانیم مثل یک آهنربا موتور نوری لیزری داشته باشیم یعنی با سرعت نور یبک الکتروموتور نوری داشته باشیم چون نور هم می تواند میدان الکترومغناطیسی داشته باشد و همزمان همان فرمولهایی که در الکترومغناطیس بر یک شاره امواج و الکتریسیته برقرار است روی امواج لیزر و نوری هم مثل امواج الکترومغناطیسی این سیستم حکم می کند و جاری است و می توان این فرمولها را استفاده کنیم با تفاوت اینکه در سیم پیچ و آهنربا امواج الکترومغناطیسی برقرار بود و در نور سیستم نوری