رسم تابع در متلب — آموزش گام به گام + نمونه کد

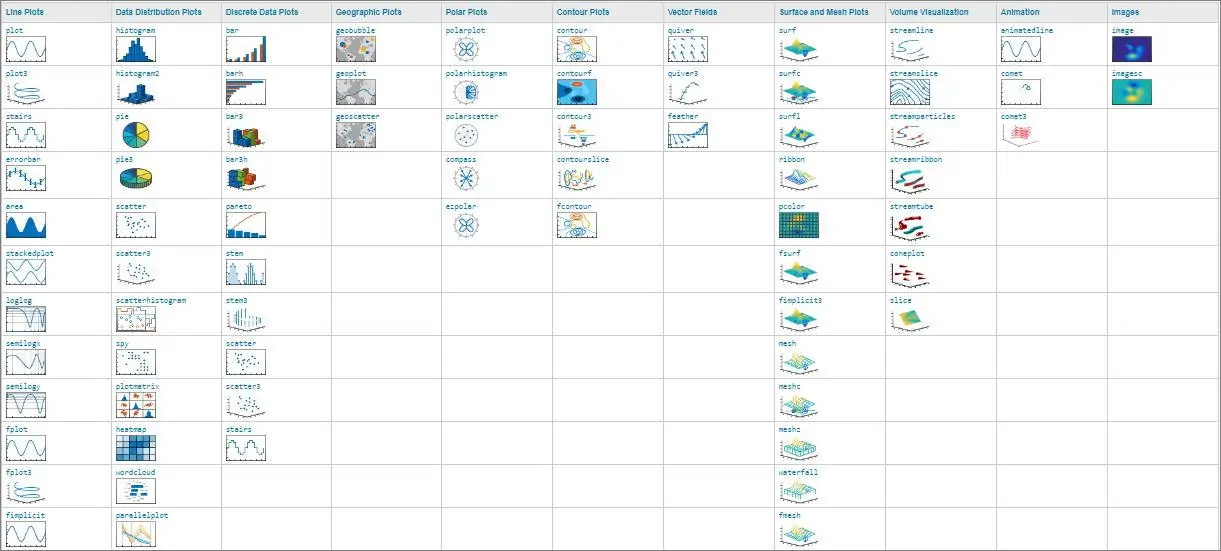
رسم تابع در متلب دستورهای مختلفی دارد که در این مطلب آن‌ها را معرفی می‌کنیم و به بررسی چند مثال و نمونه کد می‌پردازیم. به صورت کلی دستورهای رسم تابع در متلب به 11 گروه مختلف دسته‌بندی می‌شوند که هر یک ویژگی‌های خاصی دارند و نوع داده‌ای که به عنوان ورودی دریافت می‌کنند متفاوت است. انواع دستورهای رسم تابع در متلب را می‌توانید در تصویر (1) مشاهده کنید.

دستور plot

دستور plot(X،Y) یک نمودار دوبعدی از داده‌ها را در Y در برابر مقادیر مربوط به X ایجاد می‌کند. در این دستور اگر X و Y هر دو بردار باشند باید طول آن‌ها برابر باشد. اگر X و Y هر دو ماتریس باشند باید اندازه آن‌ها برابر باشد و در نتیجه دستور plot ستون‌های Y را در مقابل ستون‌های X رسم می‌کند.

اگر یکی از دو کمیت X یا Y بردار و دیگری ماتریس باشد آنگاه ماتریس باید ابعادی داشته باشد که یکی از ابعاد آن برابر با طول بردار باشد. اگر تعداد ردیف‌های ماتریس برابر با طول بردار باشد دستور plot هر ستون ماتریس را در برابر بردار رسم می‌کند. اگر تعداد ستون‌های ماتریس برابر با طول بردار باشد این دستور هر ردیف ماتریس را در مقابل بردار رسم می‌کند. اگر ماتریس یک ماتریس مربعی باشد دستور plot هر ستون را در مقابل بردار رسم می‌کند.

اگر یکی از دو کمیت X یا Y اسکالر باشد و دیگری اسکالر یا بردار باشد دستور plot یک نمودار نقاط گسسته را رسم می‌کند. با این حال برای دیدن نقاط باید یک علامت نشانگر را در دستور plot اضافه کنید و به عنوان مثال داریم: $$(X, Y, o)$$

مثال دستور plot

x را به عنوان برداری از مقادیر بین 0 و $$2\pi$$ ایجاد کنید. بین مقادیر X فاصله $$\frac{\pi}{100}$$ قرار دهید، y را نیز به عنوان سینوس مقادیر x معرفی کنید و بدین ترتیب داریم:

x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y)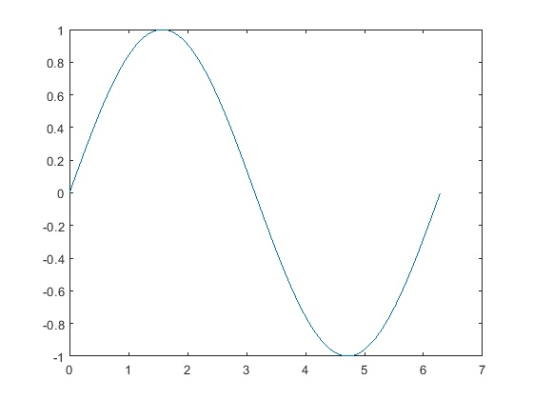

به عنوان مثال دوم x را به عنوان 100 مقدار فاصله خطی بین $$-2\pi$$ و $$2\pi$$ تعریف کنید. $$y1$$ و $$y2$$ را به عنوان مقادیر سینوس و کسینوس x معرفی کرده و یک نمودار خطی از هر دو مجموعه داده‌ها ایجاد کنید.

نمونه کدx = linspace(-2*pi,2*pi);
y1 = sin(x);
y2 = cos(x);

figure
plot(x,y1,x,y2)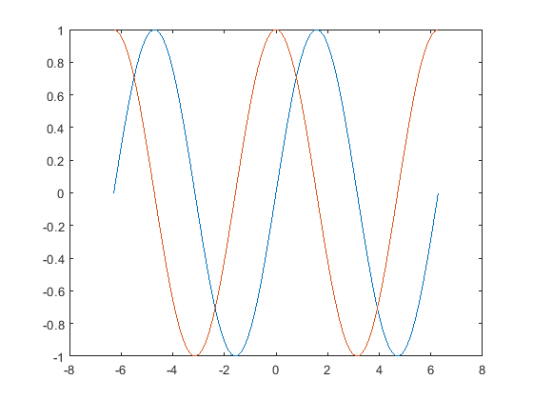

Y را به عنوان ماتریس 4 در 4 که توسط دستور magic ایجاد می‌شود تعریف کنید و آن را با دستور plot رسم کنید.

Y = magic(4);
figure
plot(Y)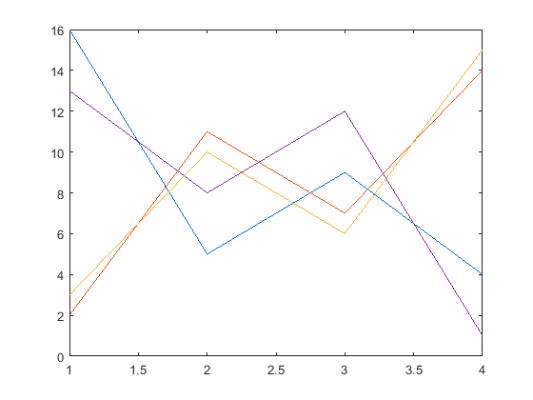

نتایج plot در هر بار اجرای کد می‌تواند متفاوت باشد زیرا دستور magic در هر بار اجرا مقادیر متفاوتی به ماتریس نسبت می‌دهد.

با مقادیر مختلفی از x که تعریف کرده‌ایم سه منحنی سینوسی را با یک تغییر فاز کوچک بین هر نمودار رسم کنید. از خط پیش فرض و سبز رنگ برای نمودار اول استفاده کنید. برای نمودار دوم یک خط چین نقطه آبی رنگ و برای نمودار سوم از نماد ستاره و رنگ فیروزه‌ای استفاده کنید و بدین ترتیب داریم:

x = 0:pi/10:2*pi;
y1 = sin(x);
y2 = sin(x-0.25);
y3 = sin(x-0.5);

figure
plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')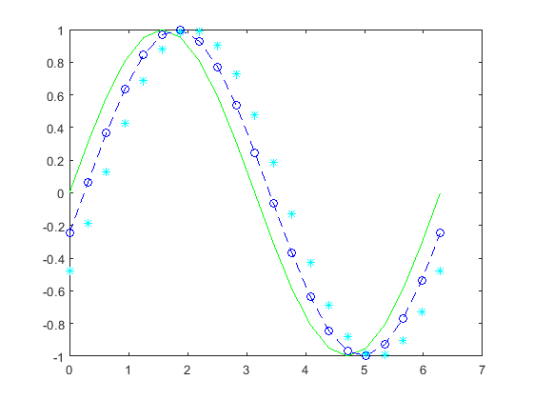

x را به عنوان 100 مقدار بین $$-2\pi$$ و $$2\pi$$ تعریف کنید. $$y1$$ و $$y2$$ را به عنوان مقادیر سینوس و کسینوس x تعریف کنید و یک نمودار خطی از هر دو مجموعه داده ایجاد کنید و دو نمودار را در متغیر p برگردانید.

x = linspace(-2*pi,2*pi);
y1 = sin(x);
y2 = cos(x);
p = plot(x,y1,x,y2);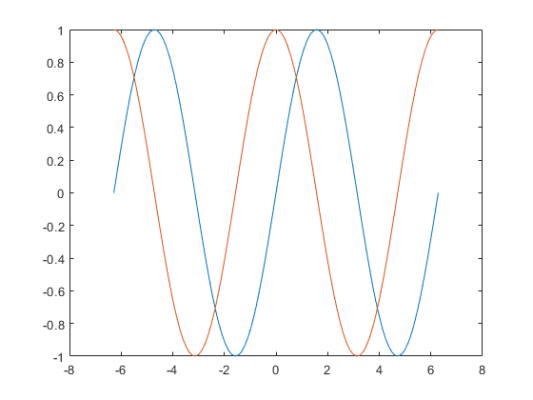

عرض اولین نمودار را به 2 تغییر دهید و نشانگرهای ستاره را به نمودار دوم اضافه کنید و بدین ترتیب داریم:

p(1).LineWidth = 2;
p(2).Marker = '*';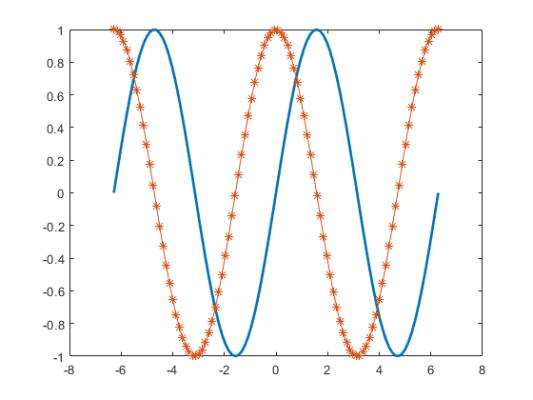

دستور plot3

plot3 (X، Y، Z) مختصات x و y و z را در فضای 3 بُعدی ترسیم می‌کند. برای رسم مجموعه‌ای از مختصات X ، Y و Z باید آن‌ها را به صورت بردارهایی با طول یکسان تعریف کنید.

همچنین برای ترسیم چند مجموعه مختصات در یک نمودار حداقل یکی از مختصات X ، Y یا Z را به عنوان ماتریس و بقیه را به عنوان بردار تعریف کنید.

مثال دستور plot3

t را به عنوان بردار مقادیر بین 0 و $$10\pi$$ تعریف کنید. st و ct را به عنوان بردار مقادیر سینوس و کسینوس تعریف کنید. سپس  st ،ct و t را رسم کنید.

t = 0:pi/50:10*pi;
st = sin(t);
ct = cos(t);
plot3(st,ct,t)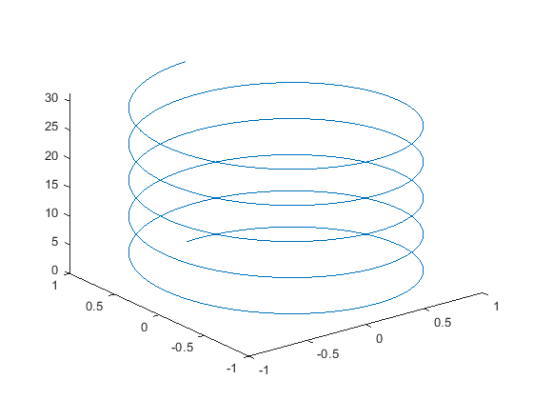

ماتریس X و Y حاوی سه ردیف مختصات است که با مقادیر t بین 0 تا $$\pi$$ به دست می‌آید.

t = 0:pi/500:pi;
X(1,:) = sin(t).*cos(10*t);
X(2,:) = sin(t).*cos(12*t);
X(3,:) = sin(t).*cos(20*t);

Y(1,:) = sin(t).*sin(10*t);
Y(2,:) = sin(t).*sin(12*t);
Y(3,:) = sin(t).*sin(20*t);

ماتریس Z حاوی مقادیر z را برای هر سه مجموعه ایجاد کنید.

Z = cos(t);

و در نهایت نمودار مقادیر (X, Y, Z) را رسم کنید:

plot3(X,Y,Z)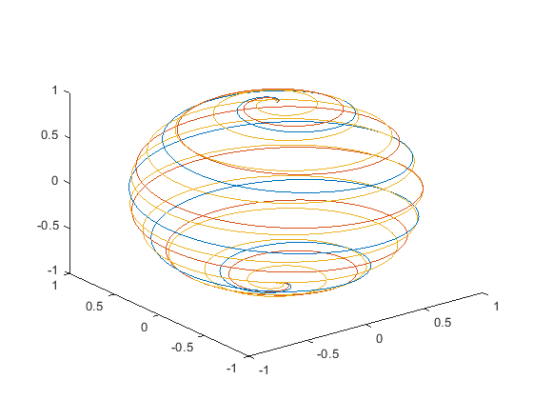

دستور stairs

stairs(Y) نمودار پله‌ای از عناصر موجود در Y را رسم می‌کند. اگر Y یک بردار باشد دستور stairs یک خط رسم می‌کنند. اگر Y ماتریس باشد دستور stairs در هر ستون ماتریس یک نمودار را می‌دهد. همچنین دستور stairs(X,Y) عناصر موجود در Y را در مکان‌های مشخص شده توسط X رسم می‌کند. ورودی‌های X و Y باید بردارها یا ماتریس‌هایی هم سایز و هم اندازه باشند. علاوه بر این  X می‌تواند یک بردار افقی یا عمودی باشد و Y باید یک ماتریس با طول تعداد ردیف‌های X باشد.

دستور stairs(___ ، LineSpec) یک سبک خط، نشانگر خط و رنگ خط را مشخص می‌کند. به عنوان مثال ورودی به صورت ': * r' یک خط قرمز نقطه‌چین با نشانگرهای ستاره را مشخص و رسم می‌کند. از این گزینه‌ها با هر یک از ترکیب‌های آرگومان ورودی برای تعیین خط رسم شده می‌توان استفاده کرد.

دستور stairs(___ ، Name ، Value) با استفاده از یک یا چند آرگومان مقدار-نام نمودار پله‌ای را تغییر می‌دهد یا اصلاح می‌کند. به عنوان مثال نمایشگر 'o' و با اندازه نمایشگر '8' در واقع نشانگر دایره‌ای با اندازه هشت را مشخص می‌کند.

دستور stairs(ax، ___) به جای محورهای مشخص شده محورهای دیگری که توسط ax مشخص شده‌اند را رسم می‌کند. ورودی ax می‌تواند قبل از هر یک از ترکیب‌های آرگومان‌های ورودی که در قسمت‌های قبلی در مورد آن‌ها صحبت شد قرار بگیرد.

دستور (___)h = stairs یک یا چند شی stairs را برمی‌گرداند. از h برای ایجاد تغییر در خصوصیات یک شی خاص Stair بعد از ایجاد آن استفاده می‌شود. [xb، yb] = stairs(___) نموداری ایجاد نمی‌کنند اما ماتریس‌های xb و yb را با همان اندازه برمی‌گردانند، سپس به عنوان مثال دستور plot(xb ، yb) نمودار پله‌ای x و y را ترسیم می‌کند.

مثال دستور stairs

یک نموادار پله‌ای سینوسی رسم کنید که فاصله بین $$0$$ تا $$4\pi$$ را به 40 قسمت مساوی تقسیم کند.

X = linspace(0,4*pi,40);
Y = sin(X);

figure
stairs(Y)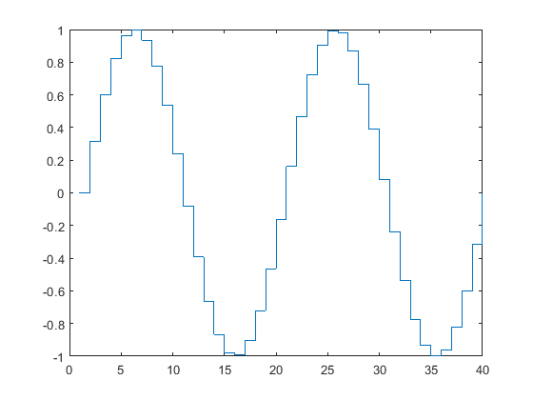

یک طرح پلکانی از دو تابع کسینوسی ایجاد کنید که فاصله بین $$0$$ تا $$4\pi$$ را به 50 قسمت مساوی تقسیم کنند. بدین ترتیب داریم:

X = linspace(0,4*pi,50)';
Y = [0.5*cos(X), 2*cos(X)];

figure
stairs(Y)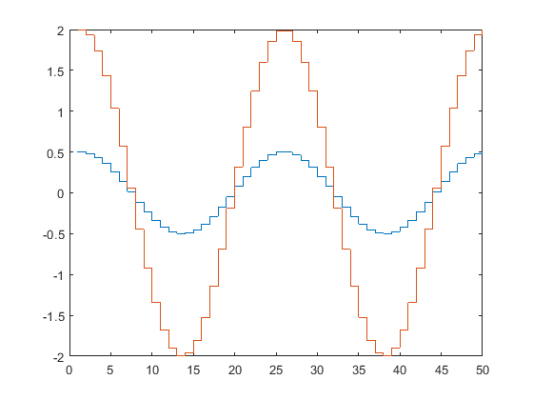

دستور errorbar

errorbar(y,err) یک نمودار خطی از داده‌های y را رسم می‌کند و یک نوار خطای عمودی را در هر نقطه از داده‌ها رسم می‌کند. مقادیر موجود در نوار خطا طول هر نوار خطا را در بالا و پایین نقاط داده تعیین می‌کنند. بنابراین کل طول میله خطا دو برابر مقادیر خطا است.

مثال دستور errorbar

بردارهای x و y را ایجاد کنید. سپس نمودار مقادیر y را در برابر مقادیر x رسم کنید. در هر نقطه از داده‌ها طول میله‌ها خطای عمودی را نشان می‌دهد که طول آن‌ها با هم برابر است.

x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = 8*ones(size(y));
errorbar(x,y,err)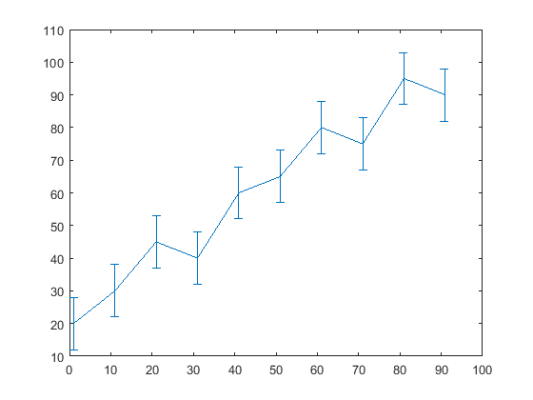

یک نمودار برای مقادیر x و y رسم کنید که مقادیر خطا در هر داده متفاوت است و خطوط errorbar به صورت افقی هستند.

x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = [1 3 5 3 5 3 6 4 3 3];
errorbar(x,y,err,'horizontal')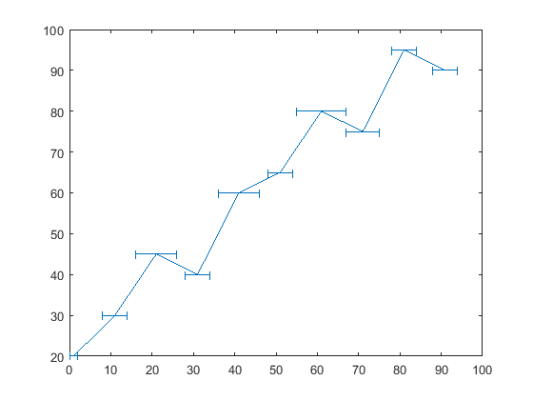

دستور area

دستور area (X، Y) مقادیر Y را در برابر مختصات x رسم می‌کند. این تابع مناطق بین منحنی‌ها را بر اساس شکل Y پر می‌کند:

• اگر Y یک بردار باشد نمودار شامل یک منحنی است. دستور area ناحیه بین منحنی و محور افقی را پر می‌کند.
• اگر Y یک ماتریس باشد نمودار شامل یک منحنی برای هر ستون در منطقه Y است. دستور area مناطق بین منحنی‌ها را پر می‌کند و آن‌ها را روی هم قرار می‌دهد که نشان‌دهنده سهم نسبی هر ردیف در ارتفاع کل در هر مختصات x است.

مثال دستور area

یک بردار از چهار مقدار ایجاد کنید و این مقادیر را با دستور area نشان دهید.

y = [1 5 6 3];
area(y)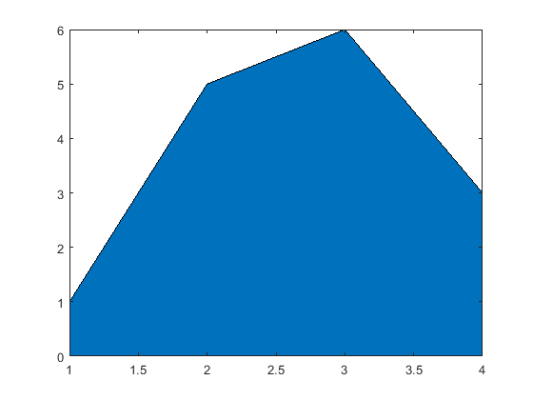

x را به عنوان برداری از سه نمایندگی فروش خودرو در نظر بگیرید. Y را به عنوان یک ماتریس حاوی تعداد اتومبیل‌های فروخته شده در هر مدل تعریف کنید. مقادیر ماتریس را توسط دستور area نمایش دهید. سپس برای هر محور یک لیبل و شرح نمودار را به دستور اضافه کنید.

x = [10 11 12];
Y = [21.6 25.4; 70.8 66.1; 58.0 43.6];
area(x,Y)
xlabel('Dealership ID')
ylabel('Sales')
legend({'Model A','Model B'})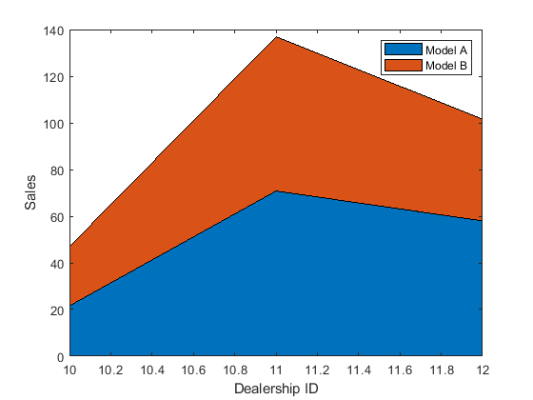

دستور stackedplot

دستور stackedplot (tbl) متغیرهای یک جدول یا یک جدول زمانی را در یک نمودار انباشته رسم می‌کند. این دستور می‌تواند حداکثر تا 25 متغیر را رسم کند. این دستور متغیرها را در محورهای جداگانه و به صورت عمودی روی هم رسم می‌کند. این متغیرها دارای محور x مشترک هستند.

• اگر tbl یک جدول است آنگاه این دستور متغیرها را در برابر اعداد سطر رسم می‌کند.
• اگر tbl یک جدول زمانی است آنگاه این دستور متغیرها را نسبت به زمان‌های سطر رسم می‌کند.

تابع stackedplot تمام متغیرهای عددی، منطقی، گروهی، روز و زمان و دوره زمانی tbl را رسم می‌کند و متغیرهای جدول را که دارای هر نوع داده دیگری هستند نادیده می‌گیرد.

مثال دستور stackedplot

داده‌ها را از یک spreadsheet بخوانید و آن‌ها را به یک جدول منتقل کنید. سپس جدول را به یک جدول زمانی تبدیل کنید. اولین متغیری که شامل تاریخ و زمان است، OutageTime ردیف زمان‌های جدول را ارائه می‌دهد. در ابتدا پنج ردیف اول را استخراج کرده و نمایش می‌دهیم:

tbl = readtable('outages.csv');
tbl = table2timetable(tbl);
head(tbl,5)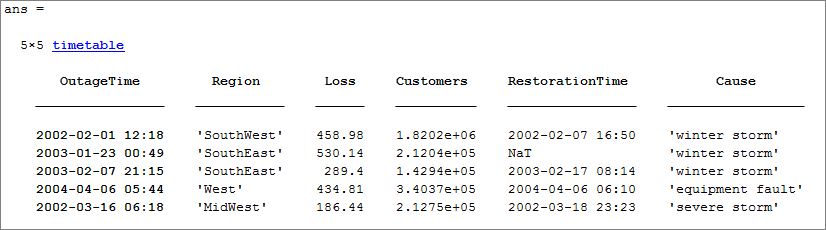

جدول را با دستور sort مرتب کنید تا بر حسب زمان مرتب شوند از کم به زیاد مرتب شوند و در نتیجه 5 ردیف ابتدایی جدول به صورت زیر نمایش داده می‌شوند:

tbl = sortrows(tbl);
head(tbl,5)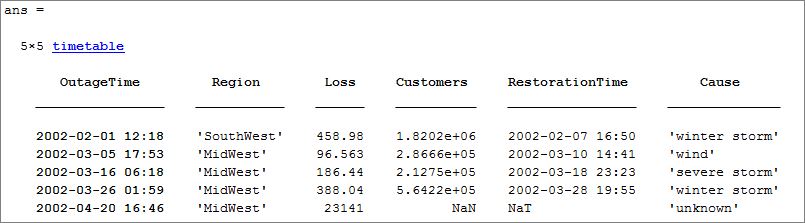

سپس یک طرح انباشته از داده‌های tbl را ایجاد کنید. ردیف زمان جدول OutageTime مقادیر در محور x ارائه می‌دهند. تابع stackedplot مقادیر متغیرهای Loss ،Customers و RestorationTime را نمایش می‌دهد و هر متغیر در امتداد محور y خود رسم می‌شود. با این حال نمودار متغیرهای Region و Cause را شامل نمی‌شود زیرا این دو ستون حاوی داده‌هایی هستند که قابلیت رسم شدن ندارند.

تصویرstackedplot(tbl)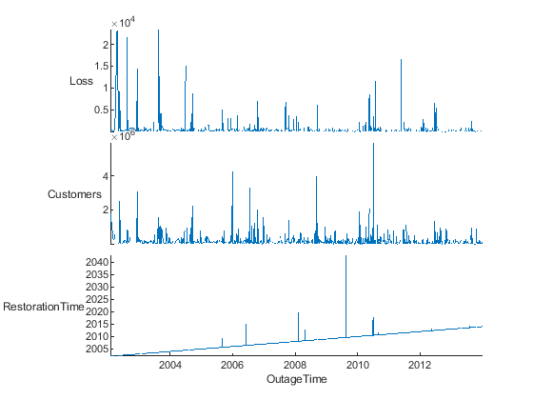

باید این نکته را بیان کرد که جدول‌ها و spredsheet‌هایی که در این مثال‌ها استفاده می‌شوند به طور پیش فرض در فایل‌های متلب موجود هستند و با دستور load به آن‌ها دسترسی پیدا خواهید کرد.

دستور loglog

دستور loglog (X، Y) مختصات x و y را با استفاده از مقیاس لگاریتمی پایه 10 در محور x و محور y رسم می‌کند.

• برای ترسیم مجموعه‌ای از مختصات مختلف که توسط یک خط به هم وصل شده باشند، باید X و Y را به عنوان بردارهایی با طول یکسان مشخص کنید.
• برای ترسیم چند مجموعه مختصات روی یک نمودار، حداقل یکی متغیرهای از X یا Y را به عنوان ماتریس مشخص کنید.

مثال دستور loglog

x را به عنوان برداری با فاصله لگاریتمی در فاصله $$[10^{-1},10^{2}]$$ تعریف کنید. y را نیز متغیری از x و به صورت $$2^{x}$$ معرفی کنید. در نهایت مقادیر x و y را با دستور loglog رسم کرده و برای نمایش خطوط در صفحه از دستور grid on استفاده کنید.

x = logspace(-1,2);
y = 2.^x;
loglog(x,y)
grid on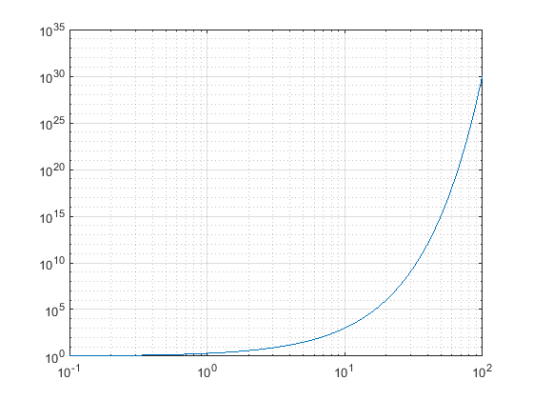

دستور semilogx

دستور semilogx(X، Y) مختصات x و y را با استفاده از مقیاس لگاریتمی پایه 10 در محور x و مقیاس خطی در محور y رسم می‌کند.

• برای ترسیم مجموعه‌ای از مختصات‌های مختلف که می‌خواهیم با یک خط به هم متصل شوند باید X و Y را به عنوان بردارهایی با طول یکسان تعریف کنیم.
• برای ترسیم چند مجموعه مختصات روی یک محور باید حداقل یکی از مختصات X یا Y را به عنوان ماتریس معرفی کرد.

مثال دستور semilogx

x را به عنوان بردار از مقادیر لگاریتمی از 0/1 تا 100 تعریف کرده و y را به عنوان کپی از x معرفی می‌کنیم. یک نمودار خطی-لگاریتمی از x و y ایجاد می‌کنیم و برای نشان دادن خطوط شبکه تابع grid فراخوانی می‌شود.

x = logspace(-1,2);
y = x;
semilogx(x,y)
grid on

دستور semilogy

دستور semilogy(X، Y) مختصات x و y را با استفاده از مقیاس خطی در محور x و مقیاس لگاریتمی پایه 10 در محور y ترسیم می‌کند. در حقیقت این دستور عکس semilogx عمل می‌کند.

• در این دستور برای ترسیم مجموعه‌ای از مختصات مختلف که توسط خط بهم وصل شوند باید X و Y را به عنوان بردارهایی با طول یکسان مشخص کرد.
• همچنین برای ترسیم چند مجموعه مختصات روی یک محور مختصات باید حداقل یکی از متغیرهای X یا Y را به عنوان ماتریس معرفی کنیم.

مثال دستور semilogy

مقادیری از x و y را به گونه‌ای ایجاد کنید که y تابعی از x بوده و نمودار را به صورت خطی-لگاریتمی رسم کنید. دقت کنید که می‌خواهیم مقادیر به صورت دایره‌هایی توپُر نمایش داده شوند که به هم متصل نبود و رنگ آن‌ها آبی پر رنگ باشد که توسط بردار سه‌تایی RGB آن را مشخص می‌کنیم. همچنین می‌خواهیم خطوط صفحه نمایش داده شوند.

x = linspace(1,1000,15);
y = (1./x) * 10000;
semilogy(x,y,'o','MarkerFaceColor',[0 0.447 0.741])
grid on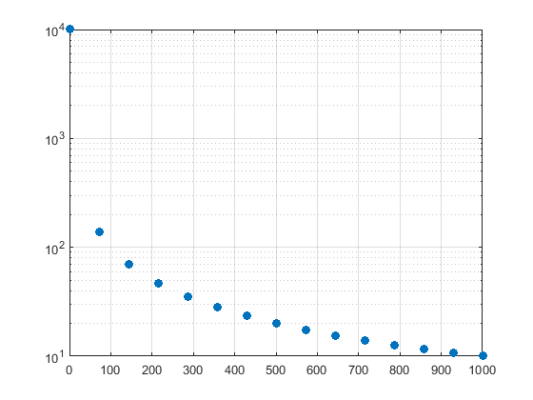

رسم تابع در متلب با دستور fplot

دستور fplot(f) منحنی تعریف شده توسط تابع y = f(x) را روی مقدار پیش فرض x که بین $$-5$$ تا $$5$$ است رسم می‌کند. این دستور مشخصاً برای رسم تابع در متلب استفاده می‌شود. اگر بخواهیم بازه تغییر x مقدار متفاوتی از $$[-5,5]$$ داشته باشد آن را به عنوان ورودی دوم به دستور تابع می‌دهیم و داریم: fplot(f, xintervals).

مثال دستور fplot

نمودار sin(x) را روی فاصله x که به صورت پیش فرض بین -5 تا 5 است، رسم کنید.

fplot(@(x) sin(x))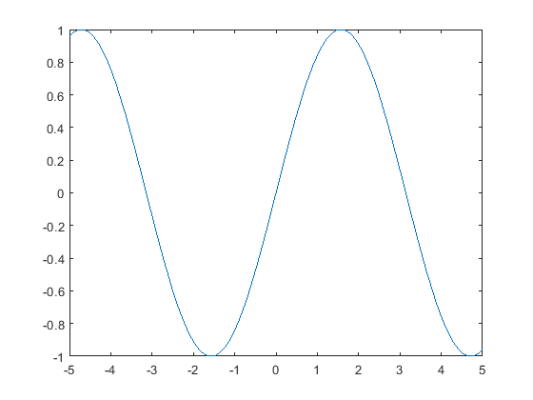

در مثال دوم می‌خواهیم منحنی پارامتری برای x = cos(3t) و y = sin (2t) را توسط دستور fplot رسم کنیم.

xt = @(t) cos(3*t);
yt = @(t) sin(2*t);
fplot(xt,yt)

به عنوان مثال سوم حالتی را در نظر بگیرید که تابع در بازه‌های مختلف مقادیر متفاوتی داشته باشد، یعنی داشته باشیم:

$$\begin{cases}e^{x} & -3<x<0\\ \cos(x) & 0<x<3\end{cases}$$

برای رسم این تابع از طریق دستور fplot از دستور hold on استفاده می‌کنیم و خط به خط تمام قسمت‌های مختلف تابع را در بازه داده شده رسم می‌کنیم. بدین ترتیب داریم:

fplot(@(x) exp(x),[-3 0],'b')
hold on
fplot(@(x) cos(x),[0 3],'b')
hold off
grid on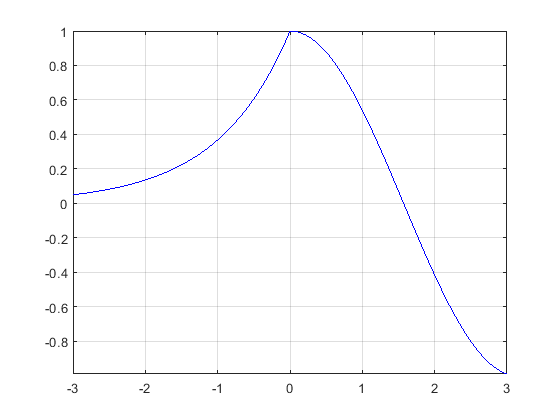

به عنوان مثال آخر از این دستور می‌خواهیم تابع $$\sin(x)$$ را در بازه $$-2\pi$$ تا $$2\pi$$ رسم کنیم و برای نمودار عنوان و برچسب قرار دهیم. بدین ترتیب داریم:

fplot(@sin,[-2*pi 2*pi])
grid on
title('sin(x) from -2\pi to 2\pi')
xlabel('x');
ylabel('y');

اگر بخواهیم مقادیر در راستای x برحسب رادیان نمایش داده شوند از دستور gca استفاده می‌کنیم تا به مقادیر در راستای x دسترسی پیدا کنیم و بدین ترتیب داریم:

ax = gca;
ax.XTick = -2*pi:pi/2:2*pi;
ax.XTickLabel = {'-2\pi','-3\pi/2','-\pi','-\pi/2','0','\pi/2','\pi','3\pi/2','2\pi'};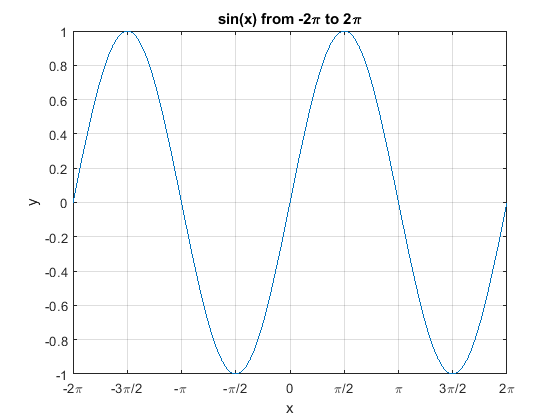

رسم تابع در متلب با دستور fplot3

دستور fplot3(funx ، funy ، funz) منحنی پارامتری تعریف شده توسط x = funx(t)، y = funy (t) و z = funz (t) را در فاصله پیش فرض بین [-5،5] برای t ترسیم می‌کند. مانند دستور قبل برای اینکه مقدار بازه پارامتر چیزی غیر از پیش فرض -5 تا 5 باشد باید این بازه را به عنوان ورودی به دستور تابع بدهیم.

مثال مربوط به دستور fplot3

خط پارامتری سه بعدی که به صورت زیر تعریف می‌شود را رسم کنید:

$$\begin{cases}x=\sin(t)\\ y=\cos(t) \\ z=t \end{cases}$$

این تابع در محدوده پیش فرض $$-5$$ تا $$5$$ رسم می‌شود.

xt = @(t) sin(t);
yt = @(t) cos(t);
zt = @(t) t;
fplot3(xt,yt,zt)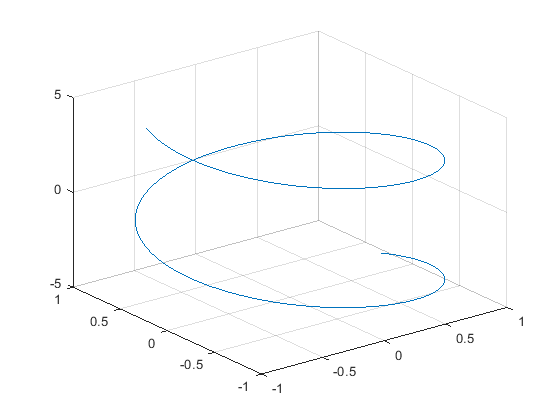

خط پارامتری زیر را با استفاده از دستور fplot3 رسم کنید.

$$\begin{cases}x=e^{-\frac{t}{10}}\sin(5t)\\ y=e^{-\frac{t}{10}}\cos(5t) \\ z=t \end{cases}$$

برای رسم این تابع از محدوده پارامتری $$[-10,10]$$ استفاده می‌کنیم

xt = @(t) exp(-t/10).*sin(5*t);
yt = @(t) exp(-t/10).*cos(5*t);
zt = @(t) t;
fplot3(xt,yt,zt,[-10 10])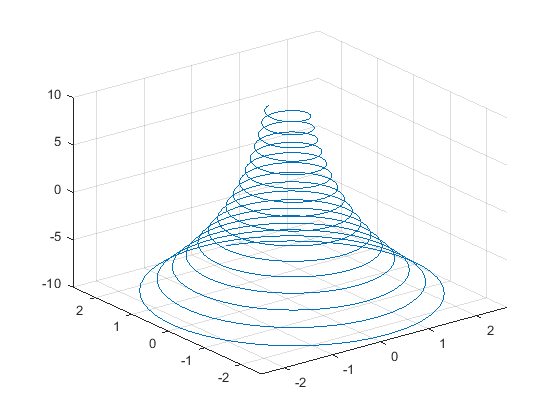

رسم تابع در متلب با دستور fimplicit

دستور fimplicit(f) تابع ضمنی تعریف شده توسط f (x، y) = 0 را روی فاصله پیش فرض $$[-5,5]$$ در راستای x و y رسم می‌کند. در واقع این دستور برای توابعی به کار می‌رود که به دو پارامتر وابسته هستند.

تابع هایپربولیک توصیف شده توسط تابع $$x^{2}-y^{2}-1=0$$ را در فاصله پیش فرض $$[-5,5]$$ برای x و y رسم کنید.

fimplicit(@(x,y) x.^2 - y.^2 - 1)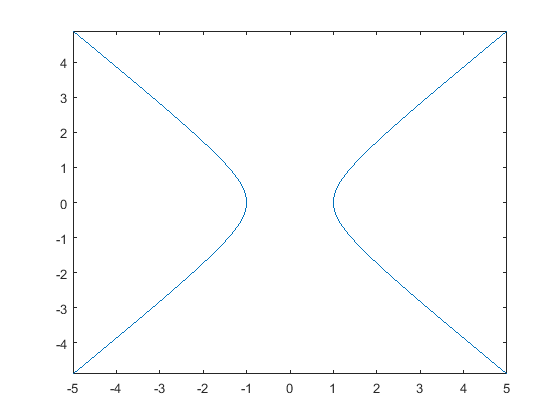

به عنوان مثال دوم دو دایره با مرکز $$(0,0)$$ با مقادیر متفاوت شعاع رسم کنید. برای اولین دایره از یک خط قرمز و نقطه‌چین استفاده کرده و برای دایره دوم از یک خط سبز و خط‌چین با عرض خط 2 استفاده کنید.

f1 = @(x,y) x.^2 + y.^2 - 1;
fimplicit(f1,':r')

hold on
f2 = @(x,y) x.^2 + y.^2 - 2;
fimplicit(f2,'--g','LineWidth',2)
hold off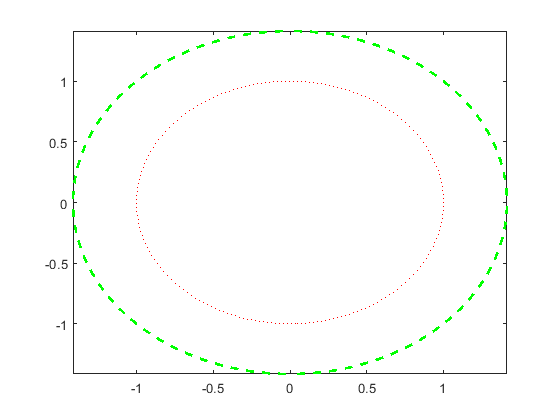

دستور histogram

هیستوگرام‌ها نوعی نمودار میله‌ای برای نمایش داده‌های عددی هستند که داده‌ها را در گروه‌های مختلف دسته‌بندی می‌کنند. بعد از ایجاد یک Histogram می‌توانید مشخصات آن هیستوگرام را با تغییر مقادیر داده‌های آن تغییر دهید. این امر به ویژه برای اصلاح سریع خواص دسته‌هایی که ایجاد کرده‌اید و یا تغییر صفحه نمایش بسیار مفید است. دستور histogram(X) یک نمودار هیستوگرام از X ایجاد می‌کند. دستور هیستوگرام از یک الگوریتم دسته‌بندی خودکار استفاده می‌کند که گروه‌های مختلف را با عرض یکسان نمایش می‌دهد. دستور هیستوگرام گروه‌ها مختلف را بصورت مستطیل نمایش می‌دهد به طوری که ارتفاع هر مستطیل تعداد عناصر موجود در آن گروه را نمایش می‌دهد.

همچنین دستور histogram(X,nbins) از تعدادی گروه مشخص شده توسط یک عدد اسکالر به nbins در رسم نمودار استفاده می‌کند.

مثال دستور histogram

10000 عدد تصادفی ایجاد کنید و یک هیستوگرام برای آن رسم کنید. دستور هیستوگرام به طور خودکار تعداد مناسبی گروه را برمی‌گزیند تا دامنه مقادیر x را پوشش دهد و شکل توزیع اساسی مقادیر را نشان دهد.

x = randn(10000,1);
h = histogram(x)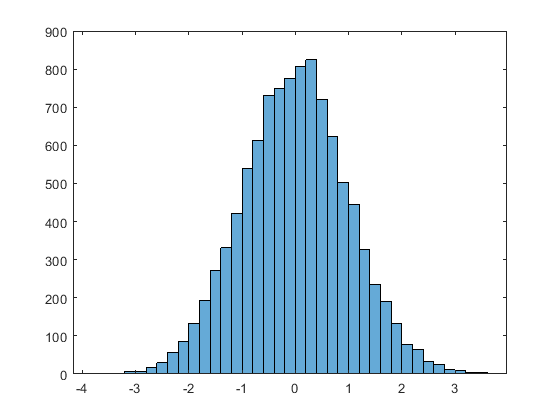

نمودار هیستوگرام را به صورتی تعریف کنید که 1000 عدد تصادفی را که در 25 گروه برابر از نظر اشغال فضا رسم کند.

x = randn(1000,1);
nbins = 25;
h = histogram(x,nbins)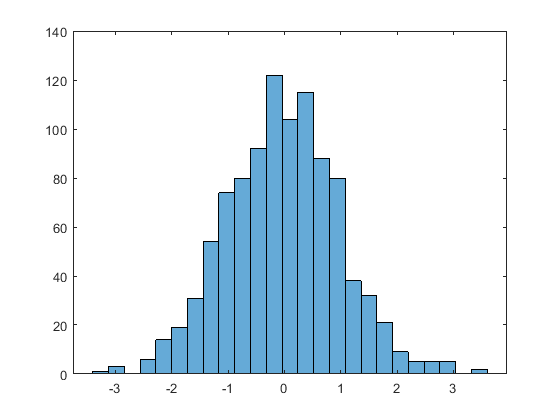

دستور histogram2

هیستوگرام‌های دو متغیره نوعی نمودار میله‌ای برای داده های عددی ایجاد می‌کنند که داده ها را به گروه‌های دو بُعدی تقسیم می‌کند. مانند دستور Histogram، بعد از ایجاد یک Histogram2 می‌توانید جنبه‌های هیستوگرام را با تغییر ویژگی‌های آن تغییر دهید. این امر به ویژه برای اصلاح سریع خواص گروه‌های طبقه‌بندی یا تغییر صفحه نمایش بسیار مفید است.

مثال دستور histogram2

1000 جفت عدد تصادفی ایجاد کنید و یک هیستوگرام متغیر ایجاد کنید. تابع histogram2 به طور خودکار تعداد مناسبی از گروه‌ها را در سطح انتخاب می‌کند تا دامنه مقادیر x و y را پوشش دهد و شکل توزیع اساسی را نشان دهد.

x = randn(10000,1);
y = randn(10000,1);
h = histogram2(x,y)
xlabel('x')
ylabel('y')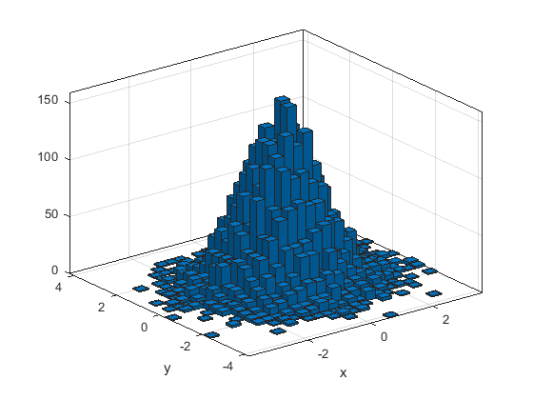

دستور pie

دستور pie(X) با استفاده از داده‌های موجود در X یک نمودار پای مانند را ترسیم می‌کند. هر برش از نمودار پای عنصری را در X نشان می‌دهد.

• اگر $$sum(X)\leq 1$$ باشد مقادیر موجود در X مستقیماً مناطق برش‌های پای را مشخص می‌کنند. دستور pie در صورتی که جمع عناصر X کوچکتر از یک باشد قسمتی از یک دایره کامل را نمایش می‌دهد.
• اگر $$sum(X)>1$$ باشد پای مقادیر $$\frac{X}{sum(X)}$$ را نرمالایز می‌کند تا مساحت هر قطعه پای را تعیین کند.
• اگر X از نوع داده‌های طبقه‌بندی شده باشد برش‌های نمودار pie با دسته‌ها مطابقت دارند و مساحت هر برش تعداد عناصر موجود در دسته تقسیم بر تعداد عناصر موجود در X است.

یک نمودار دایره‌ای از بردار X ایجاد کنید.

X = [1 3 0.5 2.5 2];
pie(X)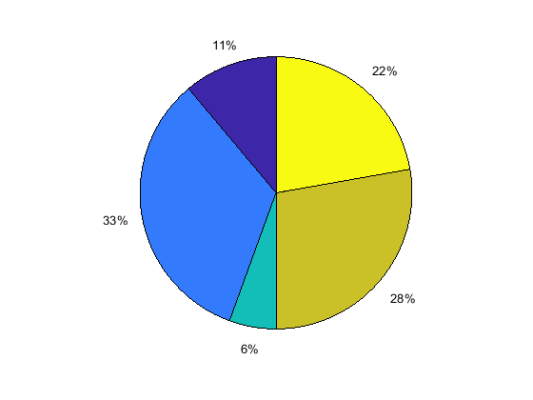

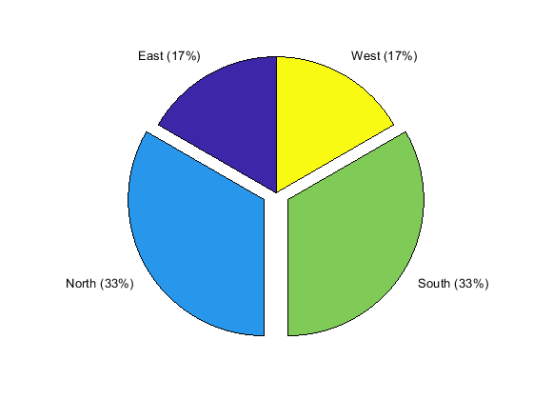
اگر بخواهیم قسمت‌های سوم و چهارم پای جدا باشند و هر قسمت برچسب خاص خودش را داشته باشد دستور را به صورت زیر تغییر می‌دهیم:

X = categorical({'North','South','North','East','South','West'});
explode = {'North','South'};
pie(X,explode)

در کد بالا قسمت‌های North و South از بقیه نواحی جدا می‌شود و نتیجه به صورت زیر خواهد بود:

دستور pie3

دستور pie3(X) با استفاده از داده های موجود در X یک نمودار پای سه بعدی ترسیم می‌کند. هر عنصر در X به عنوان یک برش در نمودار پای نمایش داده می شود.

• اگر $$sum(X)\leq 1$$ باشد مقادیر موجود در X مستقیماً ناحیه برش‌های پای را مشخص می‌کنند. در دستور pie3 در صورتی که جمع عناصر X کمتر از یک باشد قسمتی از یک دایره کامل را نشان می‌دهد.
• اگر مجموع عناصر در X بیشتر از یک باشد، دستور pie3 مقادیر را توسط $$\frac{X}{sum(X)}$$ نرمالایز می‌کند تا مساحت هر قطعه پای را تعیین کند.
• دستور pie3(X، explode) مشخص می‌کند که قطعاتی از مرکز نمودار پای جدا شوند. اگر دستور explode به عنصر (i، j) اضافه شود، عنصر X(i، j) از مرکز نمودار پای جدا می‌شوند.
• دستور pie3(... ، labels) برچسب‌های متن را برای برش‌ها مشخص می‌کند. تعداد برچسب‌ها باید با تعداد عناصر X برابر باشد.

مثال دستور pie3

یک نمودار دایره‌ای 3 بعدی از بردار x ایجاد کنید.

x = [1,3,0.5,2.5,2];
figure
pie3(x)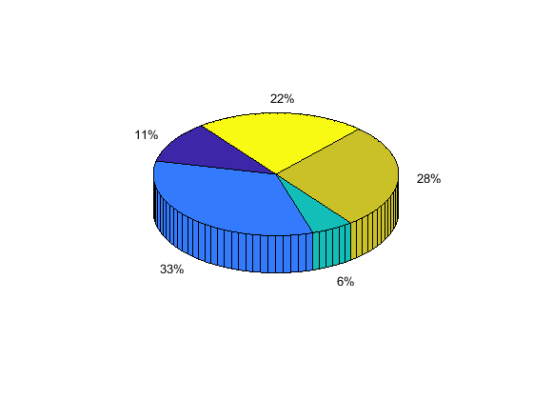

برای جدا کردن هر قطعه‌ای از نمودار pie3 از مرکز در بردار explode مقدار آن را به 1 تغییر دهید، یعنی داریم:

explode = [0,1,0,0,0];
figure
pie3(x,explode)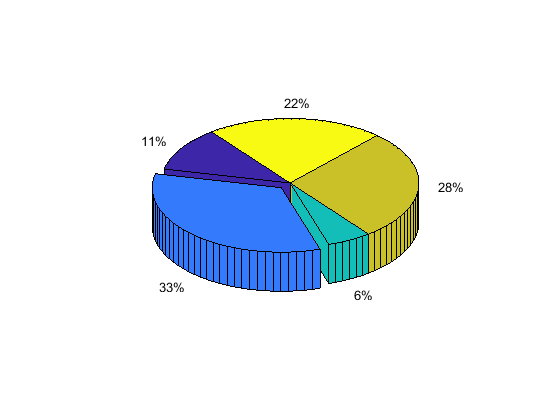

دستور scatter

دستور scatter(x، y) یک طرح پراکندگی با دایره در مکان‌های مشخص شده توسط بردارهای x و y ایجاد می‌کند. این نوع نمودار به عنوان طرح حبابدار نیز شناخته می‌شود.

مثال دستور scatter

x را به عنوان 200 مقدار با فاصله برابر بین 0 تا $$3\pi$$ ایجاد کنید و y را به عنوان مقادیر کسینوس X با نویز تصادفی معرفی کنید. با استفاده از دستور scatter مقادیر X و Y را رسم کنید.

x = linspace(0,3*pi,200);
y = cos(x) + rand(1,200);  
scatter(x,y)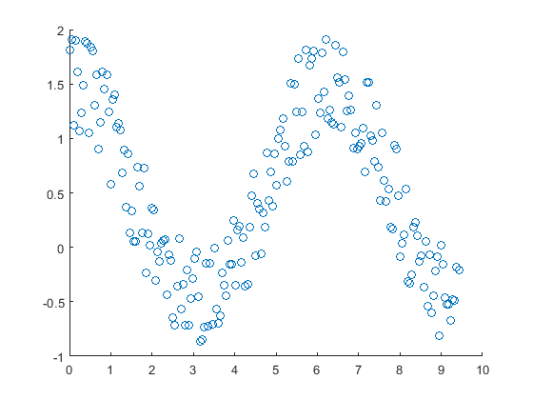

دستور scatter3

دستور scatter3(X ، Y ، Z) دایره‌هایی را در مکان‌های مشخص شده توسط بردارهای X ،Y و Z نمایش می‌دهد. همچنین دستور scatter3(X، Y، Z، S) هر دایره را با اندازه مشخص شده توسط S رسم می‌کند. برای رسم هر دایره با اندازه برابر، S را به عنوان یک اسکالر معرفی می‌کنیم. به علاوه برای رسم هر دایره با اندازه‌ای خاص S را به عنوان بردار مشخص خواهیم کرد.

دستور scatter3(X,Y,Z,S,C) هر دایره با رنگ مشخص شده در C رسم می‌کند.

• اگر C یک سه گانه RGB یا بردار کاراکتر یا رشته‌ای حاوی یک نام رنگ باشد تمام دایره‌ها با رنگ مشخص رسم می‌شوند.
• اگر C یک ماتریس سه ستونی با تعداد ردیفی برابر با طول X ،Y و Z باشد، در این حالت هر ردیف C کد رنگ RGB را برای هر دایره مربوطه مشخص می‌کند.
• اگر C یک بردار با طول برابر با طول X ،Y و Z باشد، آن گاه مقادیر C به صورت خطی با رنگ‌های موجود در نقشه رنگ فعلی ترسیم می‌شوند.

یک طرح پراکندگی سه بُعدی ایجاد کنید و برای تعریف بردارهای x ،y و z از کره استفاده کنید.

figure
[X,Y,Z] = sphere(16);
x = [0.5*X(:); 0.75*X(:); X(:)];
y = [0.5*Y(:); 0.75*Y(:); Y(:)];
z = [0.5*Z(:); 0.75*Z(:); Z(:)];
scatter3(x,y,z)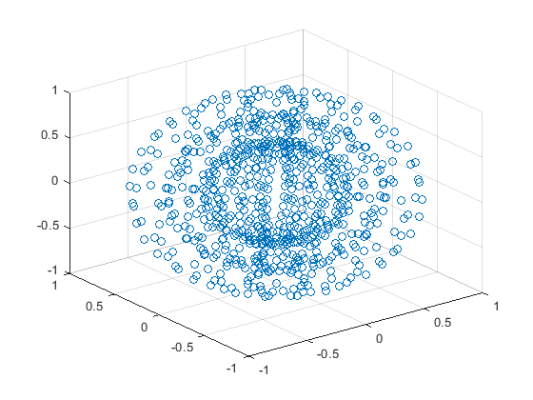

x ، y و z را که از دستور sphere ساخته شده‌اند را با اندازه و رنگ مشخص رسم کنید:

[X,Y,Z] = sphere(16);
x = [0.5*X(:); 0.75*X(:); X(:)];
y = [0.5*Y(:); 0.75*Y(:); Y(:)];
z = [0.5*Z(:); 0.75*Z(:); Z(:)];
S = repmat([50,25,10],numel(X),1);
C = repmat([1,2,3],numel(X),1);
s = S(:);
c = C(:);
figure
scatter3(x,y,z,s,c)
view(40,35)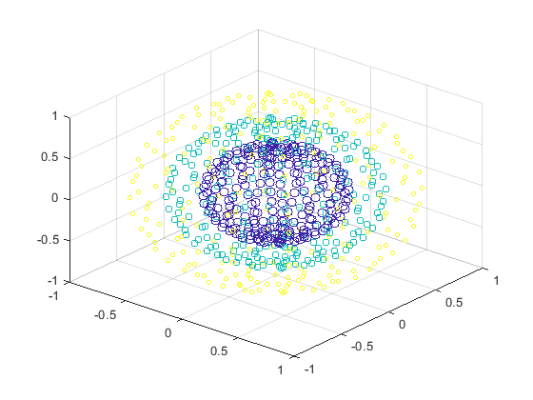

دستور scatterhistogram

دستور scatterhistogram(tbl ، xvar ، yvar) یک نمودار پراکنده با یک نمودار هیستوگرام‌های از جدول tbl ایجاد می‌کند. ورودی xvar متغیر جدول را برای نمایش در امتداد محور x نشان می‌دهد و ورودی yvar متغیر جدول را برای نمایش در امتداد محور y نمایش می‌دهد.

مثال دستور scatterhistogram

یک نمودار پراکنده با هیستوگرام‌ از جدول داده‌های مربوط به بیماران پزشکی ایجاد کنید. برای این کار مجموعه داده‌های بیماران را در متلب با دستور load بارگذاری کرده (داده‌های patients در فایل‌های متلب موجود است) و یک جدول از زیرمجموعه متغیرهای بارگیری شده در فضای کار ایجاد می‌کنیم. سپس یک نمودار هیستوگرام پراکنده ایجاد کنید که مقادیر Height را با مقادیر Weight مقایسه کند.

load patients
tbl = table(LastName,Age,Gender,Height,Weight);
s = scatterhistogram(tbl,'Height','Weight');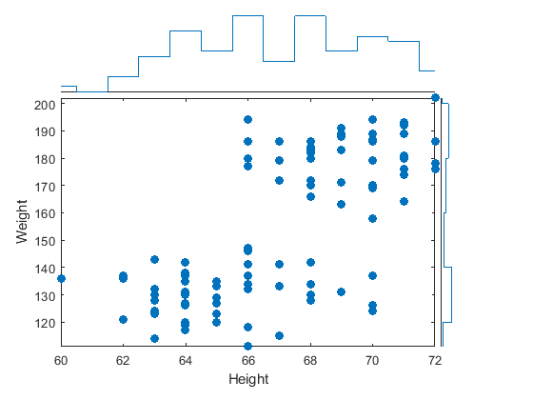

دستور spy

spy(S) الگوی پراکندگی ماتریس S را رسم می‌کند مقادیر غیر صفر رنگی هستند در حالی که مقادیر صفر سفید هستند. نمودار تعداد عناصر غیر صفر ماتریس S را نشان می‌دهد ;که با دستور nz = nnz (S) به دست می‌آید.

مثال دستور spy

نمودار ماتریس sparse پراکنده 60 در 60 متصل مربوط به ژئودزیک «باکمینستر فولر» (Buckminster Fuller) را ترسیم کنید. این ماتریس همچنین نشان دهنده مولکول کربن -60 و یک توپ فوتبال است.

B = bucky;
spy(B)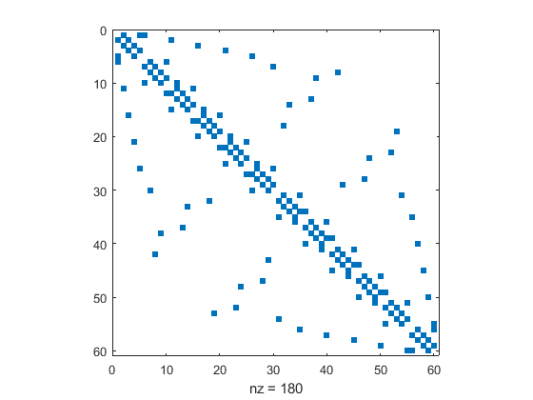

دستور plotmatrix

در مورد این دستور جزئیات و توضیحات آن مطلب رسم نمودار ماتریس در متلب | گام به گام و کاربردی را مطالعه کنید.

دستور wordcloud

دستور wordcloud(tbl، wordVar، sizeVar) یک نمودار ابر مانند از کلمات جدول tbl ایجاد می‌کند. متغیرهای wordVar و sizeVar در جدول به ترتیب کلمات و اندازه کلمات را مشخص می‌کنند.

مثال دستور wordcloud

مثال sonetetsTable را که در فایل‌های متلب موجود است را load کنید. جدول tbl شامل لیستی از کلمات در متغیر Word و تعداد تکرار مربوطه در متغیر Count است.

load sonnetsTable
head(tbl)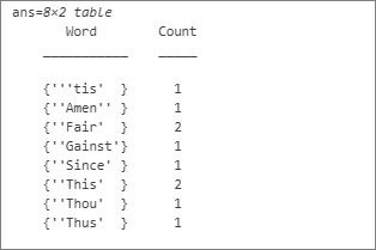

نمودار جدول را با استفاده از wordcloud رسم می‌کنیم. کلمات و اندازه کلمات مربوطه را به ترتیب با متغیرهای Word و Count مشخص کنید.

figure
wordcloud(tbl,'Word','Count');
title("Sonnets Word Cloud")

دستور parallelplot

parallelplot(tbl) یک نمودار مختصات موازی از جدول tbl ایجاد می‌کند. هر خط در نمودار یک ردیف در جدول را نشان می‌دهد و هر متغیر مختصات در نمودار مربوط به یک ستون در جدول است. این نرم افزار به طور پیش‌فرض تمام ستون‌های جدول را ترسیم می‌کند.

مثال دستور parallelplot

یک نمودار مختصات موازی از جدول داده‌های patients را که در فایل‌های متلب وجود دارد ایجاد کنید. برای این کار در ابتدا مجموعه داده‌های بیماران را توسط دستور load بارگذاری کنید و در فضای کار متلب از زیرمجموعه متغیرهای بارگیری شده یک جدول ایجاد کنید. در نهایت با استفاده از جدول نمودار مختصات موازی ایجاد کنید. خطوط موجود در نمودار مربوط به هر یک از بیماران است. برای مشاهده روند تغییر داده‌ها از نمودار استفاده کنید. به عنوان مثال نمودار نشان می‌دهد که میزان فشار خون در افراد سیگاری بیشتر است (هم دیاستولیک و هم سیستولیک).

load patients
tbl = table(Diastolic,Smoker,Systolic);
p = parallelplot(tbl)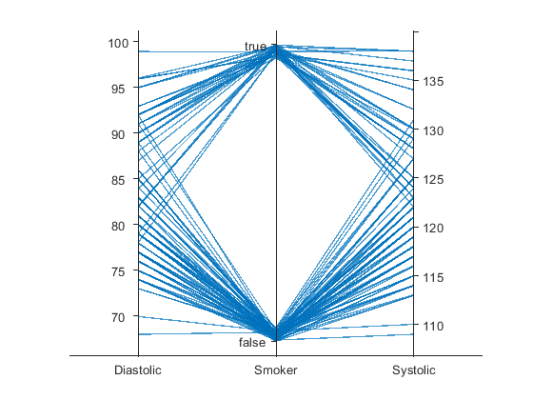

دستور bar

دستور bar(y) یک نمودار میله‌ای با یک نوار برای هر عنصر در y ایجاد می‌کند. اگر y یک ماتریس m در n باشد آن گاه میله‌ها m گروه n میله‌ای را ایجاد می‌کنند.

مثال دستور bar

y = [75 91 105 123.5 131 150 179 203 226 249 281.5];
bar(y)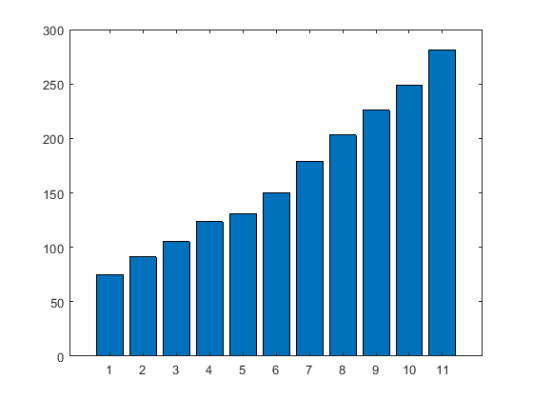

دستور barh

barh(y) یک نمودار میله‌ای افقی با یک نوار برای هر عنصر در y ایجاد می‌کند. اگر y یک ماتریس m در n باشد دستور barh تعداد m گروه n میله‌ای ایجاد می‌کند.

یک بردار از چهار مقدار ایجاد کنید. مقادیر را در یک نمودار میله‌ای با یک نوار افقی برای هر مقدار نمایش دهید.

y = [10 20 30 41];
barh(y)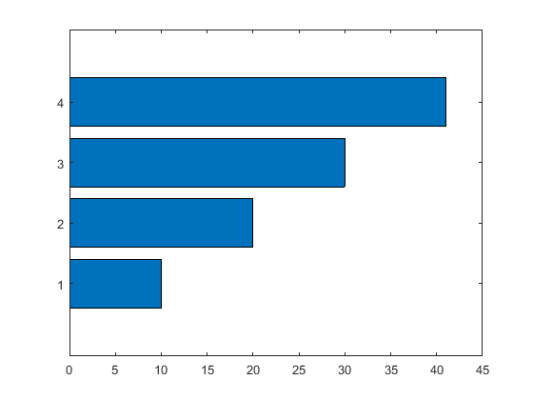

دستور bar3

دستور bar3 یک نمودار میله‌ای سه بعدی ترسیم می‌کند. دستور bar3(Z) یک نمودار میله‌ای سه بعدی ترسیم می‌کندکه هر عنصر در Z مربوط به یک نوار است. وقتی Z یک بردار باشد مقیاس محور y از 1 تا length(Z) متغیر است. وقتی Z ماتریس است مقیاس محور y از 1 تا تعداد ردیف‌های Z متغیر است. دستور bar3(Y، Z) یک نمودار میله‌ای از عناصر را در Z در مکان‌های مشخص شده در Y ترسیم می‌کند. زمانی که Y یک بردار است مقادیر y اندازه میله‌های عمودی را تعریف می‌کنند. مقادیر y می‌توانند غیرمونوتونیک باشد اما نمی‌تواند حاوی مقادیر تکراری باشد. اگر Z ماتریس باشد عناصر یک ردیف در Z در همان مکان در امتداد محور y ظاهر می‌شوند.

دستور bar3(...،width) عرض میله‌ها را تنظیم می‌کند و جداسازی میله‌ها را در یک گروه کنترل می‌کند. عرض پیش فرض $$0.8$$ است و میله‌ها با این فاصله از هم جدا می‌شوند. اگر عرض میله‌ها 1 باشد میله‌های داخل با یکدیگر در تماس خواهند بود.

دستور bar3(...،style) سبک میله‌ها را مشخص می‌کند. سبک میله‌ها شامل detached، grouped یا stacked است. حالت پیش فرض نمایش این دستور detached است.

• detached عناصر هر سطر را در Z به عنوان بلوک‌های جداگانه پشت سر هم در جهت x نمایش می‌دهد.
• grouped در حقیقت n گروه از میله‌های عمودی m را نمایش می‌دهد که n تعداد سطرها و m تعداد ستون‌های Z است. هر گروه شامل یک نوار در هر ستون در Z است.
• stacked یک نوار برای هر ردیف در Z نشان می‌دهد. ارتفاع میله مجموع عناصر موجود در ردیف است. هر میله چند رنگ است و رنگ‌ها مربوط به عناصر مشخص هستند و سهم نسبی هر عنصر ردیف را در مجموع عناصر نشان می‌دهند.
• bar3(... ،color) تمام میله‌ها را با استفاده از رنگ مشخص شده توسط color نمایش می‌دهد. به عنوان مثال از r برای نوارهای قرمز استفاده می‌شود. آیتم color با یکی از این حروف مشخص می‌شود: r، g، b، c، m، y، یا w.
• bar3(ax، ...) به جای محورهای فعلی ax را جایگزین جدید قرار می‌دهد.
• (...)h = bar3 برداری از اشیا را به سطح برمی‌گرداند. وقتی Z ماتریس است bar3 در هر ستون یک شی در سطح ایجاد می‌کند.

مثال دستور bar3

مجموعه داده‌های count.dat را از فایل‌های متلب با دستور load بارگذاری کنید که این داده‌ها یک ماتریس سه ستونی را برمی‌گردانند. Z را به عنوان 10 ردیف اول فایل count ذخیره کنید و سپس با استفاده از دستور bar3 این 10 ردیف را رسم کنید.

load count.dat
Z = count(1:10,:);
figure
bar3(Z)
title('Detached Style')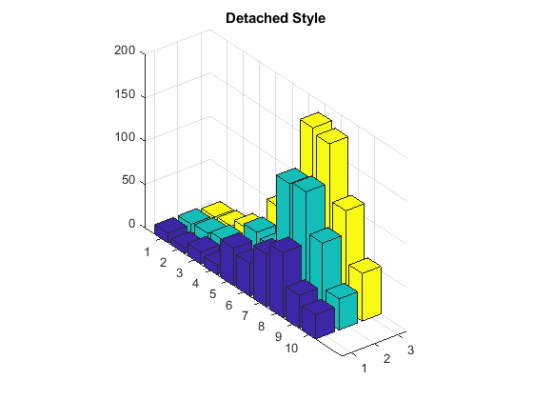

دستور bar3h

دستور bar3h نمودارهای میله‌ای افقی سه بعدی ترسیم می‌کند. تمام جزئیات این دستور مشابه دستور bar3 است.

مثال مربوط به دستور bar3h

دوباره فایل count.dat را با استفاده از دستور load در صفحه کار متلب بارگذاری می‌کنیم و 10 ستون ابتدایی آن را تحت عنوان Y ذخیره می‌کنیم. با استفاده از دستور bar3h آن را ترسیم می‌کنیم.

load count.dat
Y = count(1:10,:);
figure
bar3h(Y)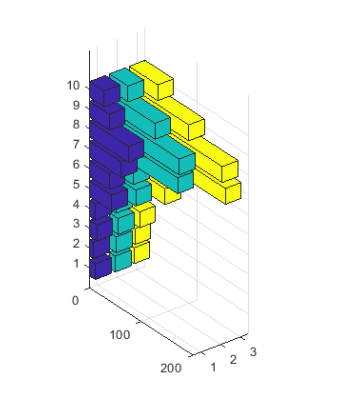

دستور pareto

نمودارهای پارتو مقادیر موجود در بردار Y را به صورت میله‌هایی که به ترتیب نزولی رسم شده‌اند نشان می‌دهند. مقادیر Y باید غیرمنفی باشد و شامل NaN نباشد. به طور پیش فرض بلندترین 10 میله ابتدایی یا 95٪ اول از توزیع تجمعی (هر یک که کوچکتر باشند) نمایش داده می‌شوند.

• pareto(Y) هر میله را با شاخص عنصر خود در Y نمایش می‌دهد و همچنین یک خط را رسم می‌کند که مجموع تجمعی Y را نشان می‌دهد.
• pareto (Y ، names) هر نوار را با متن مرتبط در نام آرایه ماتریس یا سلول نامگذاری می‌کند.
• pareto (Y، X) هر نوار را با مقدار مرتبط از X نامگذاری می‌کند.
• pareto (ax، ..) به جای محورهای فعلی ax، براساس ax جدید رسم می‌شود.
• pareto (... ،threshold) مقدار آستانه بین 0 تا 1 را مشخص می‌کند. آستانه کسری از هیستوگرام تجمعی است که در نمودار گنجانده شده است. نمودار بدون در نظر گرفتن مقدار آستانه حداکثر ده نوار را نشان می دهد.
• (...) H = pareto یک شی که شامل یک خط و یک نمودار bar مانند است را برمی‌گرداند.
• [H ، ax] = pareto (...) علاوه بر objectهای دستور بالا دو محور نیز به عنوان شی تولید می‌کند.

مثال دستور pareto

یک نمودار پرتو با استفاده از داده‌های ورودی رسم کنید.

y = [90,75,30,60,5,40,40,5];
figure
pareto(y)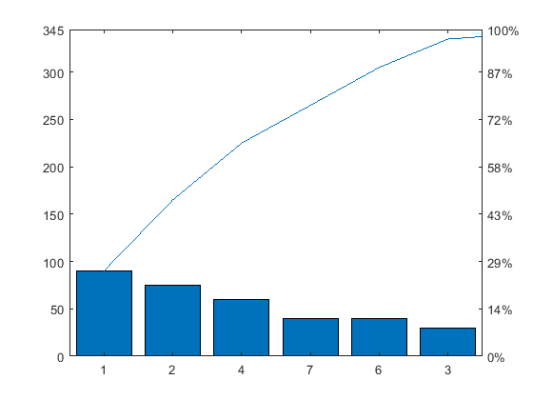

pareto عناصر موجود در y را به ترتیب در نوارهایی به صورت نزولی نمایش می‌دهد و هر نوار را با شاخص خود در y نامگذاری می‌کند. از آنجا که pareto تنها $$95\%$$ اول از توزیع تجمعی را نمایش می‌دهد برخی از عناصر y نمایش داده نمی‌شوند.

دستور stem

دستور stem(Y) توالی داده‌های Y را به عنوان ساقه‌هایی که از یک خط پایه در امتداد محور x امتداد می‌یابند را ترسیم می‌کند. مقادیر داده‌ها با حلقه‌هایی که هر پایه را خاتمه می‌دهند نشان داده می‌شوند.

• اگر Y یک بردار باشد مقیاس محور x از 1 تا length(Y) متغیر است.
• اگر Y یک ماتریس باشد stem همه عناصر را در یک ردیف در برابر مقدار x یکسان ترسیم می‌کند و مقیاس محور x از 1 تا تعداد ردیف‌های Y متغیر است.
• stem(X، Y) توالی داده‌های Y را در مقادیر مشخص شده توسط X رسم می‌کند. ورودی‌های X و Y باید بردار یا ماتریس یک اندازه باشند. علاوه بر این X می‌تواند یک بردار ردیف یا ستون باشد و Y باید یک ماتریس با طول ردیف X باشد.
• اگر X و Y هر دو بردار هستند پس ورودی‌های Y را در برابر ورودی‌های مربوط به X ترسیم می‌كنیم.
• اگر X یک بردار و Y یک ماتریس است دستور stem ستون‌های Y را در برابر مجموعه مقادیر مشخص شده توسط X رسم می‌کند، بدین ترتیب تمام عناصر در یک ردیف Y به ازای یک مقدار یکسان رسم می‌شوند.
• اگر X و Y هر دو ماتریس باشند، ستون‌های Y را در ستون‌های مربوط به X رسم می‌کنیم.

مثال مربوط به دستور stem

یک نمودار stem از 50 داده بین $$-2\pi$$ و $$2\pi$$ را رسم کنید.

figure
Y = linspace(-2*pi,2*pi,50);
stem(Y)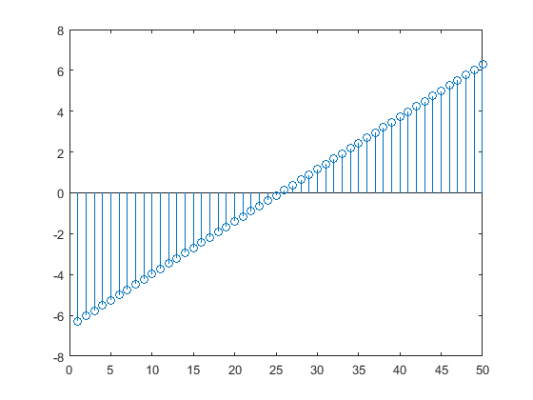

دستور stem3

دستور stem3(Z) ورودی‌های Z را به صورت ساقه‌هایی که از صفحه xy امتداد یافته اند و با دایره‌ها در آخرین مقادیر ورودی نمایش داده می‌شوند رسم می‌شود. مکان‌های ساقه در صفحه xy به طور خودکار تولید می‌شوند.

مثال دستور stem3

یک نمودار stem سه‌بعدی از مقادیر کسینوس بین $$-\frac{\pi}{2}$$ و $$\frac{\pi}{2}$$ را رسم کنید.

figure
X = linspace(-pi/2,pi/2,40);
Z = cos(X);
stem3(Z)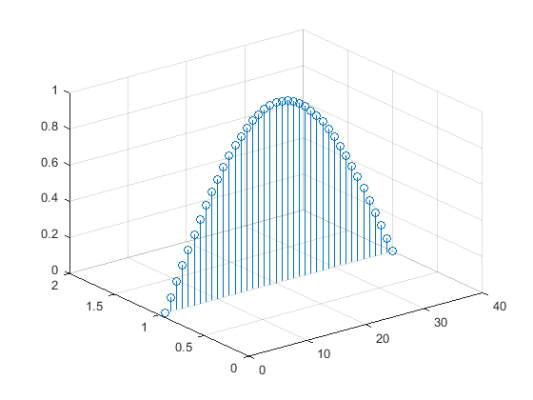

رسم تابع در متلب با دستور polarplot

دستور polarplot(theta، rho) یک خط را در مختصات قطبی رسم می‌کند. در این خط theta زاویه را برحسب رادیان بیان می‌کند و rho مقدار شعاع برای هر نقطه است. ورودی‌ها باید بردارهایی با طول برابر یا ماتریس‌هایی با اندازه برابر باشند. اگر ورودی‌ها ماتریس باشند دستور polarplot ستون‌های rho را در مقابل ستون‌های theta رسم می‌کند. همچنین یکی از ورودی‌ها می‌تواند بردار و دیگری می‌تواند ماتریس باشد به شرطی که بردار طول یک بعد ماتریس را داشته باشد.

• دستور polarplot (theta، rho ، LineSpec) نوع خط، نشانگر خط و رنگ را برای خط تعیین می‌کند.
• دستور polarplot(theta1 ، rho1 ، ... ، thetaN ، rhoN) چندین جفت rho و theta را ترسیم می‌کند.
• دستور polarplot (theta1 ، rho1 ، LineSpec1 ، ... ، thetaN ، rhoN ، LineSpecN) نوع خط، نشانگر خط و رنگ را برای هر خط مشخص می‌کند.
• دستور polarplot(rho) مقادیر شعاع در rho را در زاویه‌هایی با فاصله مساوی بین 0 و $$2\pi$$ ترسیم می‌کند.
• دستور polarplot(rho ، LineSpec) سبک خط، نشانگر خط و رنگ خط را تعیین می‌کند.
• دستور polarplot(Z) مقادیر مختلط در Z را ترسیم می‌کند.
• دستور polarplot(Z ، LineSpec) سبک خط، نشانگر و رنگ را برای خط تعیین می‌کند.
• دستور polarplot(___ ، Name ، Value) خصوصیات خط نمودار را با استفاده از یک یا چند آرگومان Name و Value مشخص می‌کند. تنظیمات این ویژگی‌ها برای همه خطوط اعمال می‌شود. دقت کنید که با استفاده از جفت‌های Name و Value نمی‌توانید مقادیر مختلف ویژگی را برای خطوط مختلف تعیین کنید.
• دستور polarplot(pax ، ___) به جای محورهای فعلی از شی PolarAxes مشخص شده توسط pax استفاده می‌کند.
• دستور (___)p = polarplot یک یا چند شی نمودار را برمی‌گرداند. می‌توانید از p برای تعیین خصوصیات یک شی نمودار خاص استفاده کنید.

مثال دستور polarplot

یک خط را در مختصات قطبی رسم کنید.

theta = 0:0.01:2*pi;
rho = sin(2*theta).*cos(2*theta);
polarplot(theta,rho)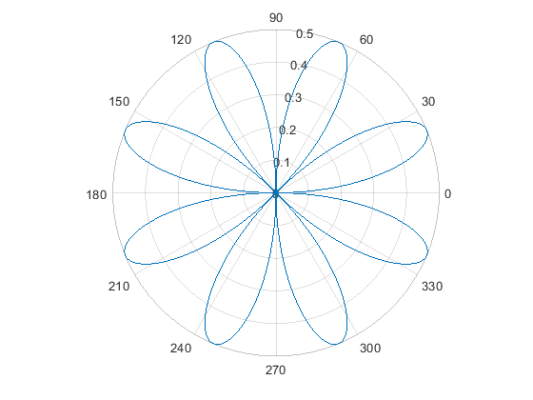

دو خط را در مختصات قطبی رسم کنید و برای خط دوم از خطوط خط‌چین استفاده کنید.

theta = linspace(0,6*pi);
rho1 = theta/10;
polarplot(theta,rho1)

rho2 = theta/12;
hold on
polarplot(theta,rho2,'--')
hold off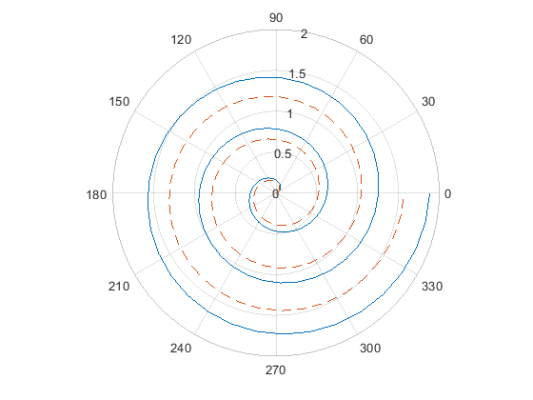

دستور polarhistogram

دستور polarhistogram (theta) با مرتب سازی مقادیر موجود در تتا به گرو‌ه‌های یکسان از لحاظ فاصله یک نمودار هیستوگرام را در مختصات قطبی ایجاد می‌کند. مقادیر در theta به رادیان مشخص می‌شوند.

مثال دستور polarhistogram

یک بردار از مقادیر بین 0 تا $$2\pi$$ ایجاد کرده و داده‌ها را در 6 گروه دسته‌بندی کنید.

theta = [0.1 1.1 5.4 3.4 2.3 4.5 3.2 3.4 5.6 2.3 2.1 3.5 0.6 6.1];
polarhistogram(theta,6)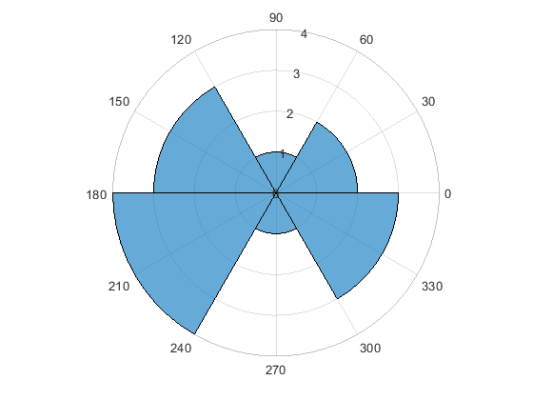

دستور polarscatter

دستور polarscatter(th، r) نمودار th در مقابل r را نمایش می‌دهد و در هر نقطه یک دایره را رسم می‌کند. th و r باید بردارهایی با طول یکسان باشند و th بر حسب رادیان مشخص می‌شود.

مثال دستور polarscatter

یک نمودار پراکنده را در مختصات قطبی رسم کنید.

th = pi/4:pi/4:2*pi;
r = [19 6 12 18 16 11 15 15];
polarscatter(th,r)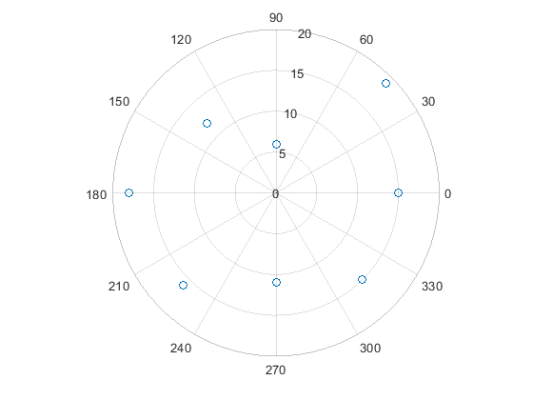

دستور compass

دستور compass(U ، V) پیکان‌هایی را نشان می‌دهد که مبداء آن‌ها مرکز مختصات یا نقطه (0,0) است. جهت فلش‌ها با استفاده از مختصات دکارتی U و V مشخص می‌شود، U مختصات x و V مختصات y را نمایش می‌دهد. تعداد پیکان‌ها با تعداد عناصر موجود در U مطابقت دارد.

دستور قطب نما یا compass فلش‌ها را بر روی یک شبکه دایره‌ای شکل با محور theta و r ترسیم می‌کند. بنابراین مختصاتی که به عنوان ورودی مشخص می‌کنید با نامگذاری‌های نمایش داده شده در نمودار مطابقت ندارند.

مثال دستور compass

با استفاده از مختصات قطبی یک قطب نما ایجاد کنید. در ابتدا با استفاده از دستور pl2cart مختصات قطبی را به کارتزین تبدیل کنید و سپس نمودار را رسم کنید.

th = linspace(pi/4,2*pi,10);
r = linspace(5,20,10);
[u,v] = pol2cart(th,r);
compass(u,v)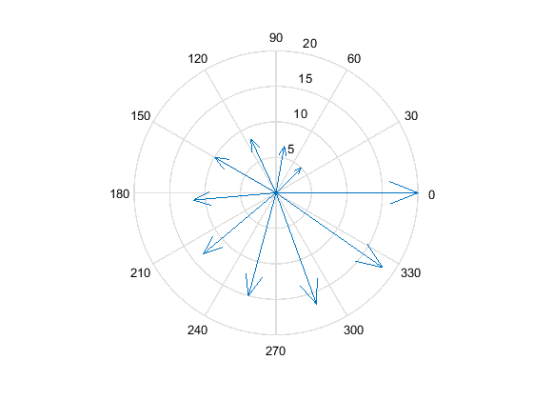

رسم تابع در متلب با دستور ezpolar

دستور ezpolar(fun) منحنی قطبی rho = fun(theta) را روی دامنه پیش فرض $$0<theta<2\pi$$ رسم می‌کند. fun می‌تواند یک تابع، یک بردار یا یک رشته باشد. دستور ezpolar(fun ، [a ، b]) تابع را در بازه $$a<theta<b$$ رسم می‌کند. همچنین دستور ezpolar(axes_handle، ...) به جای محورهای فعلی بر روی محورهای axes_handle تغییرات اعمال می‌کند و در نهایت دستور (___)h = ezpolar یک شی به نام h ایجاد می‌کند.

مثال دستور ezpolar

تابع $$\cos(t)+1$$ را روی دامنه $$[0,2\pi]$$ رسم کنید.

figure
ezpolar('1+cos(t)')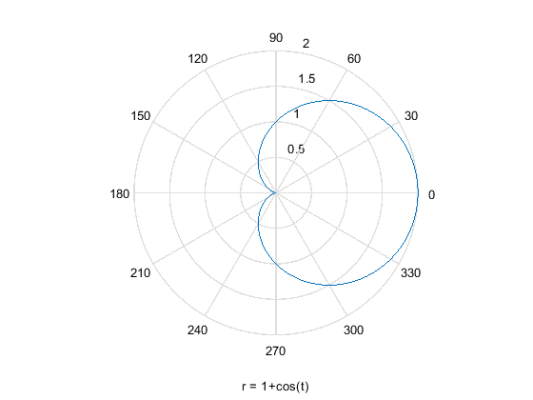

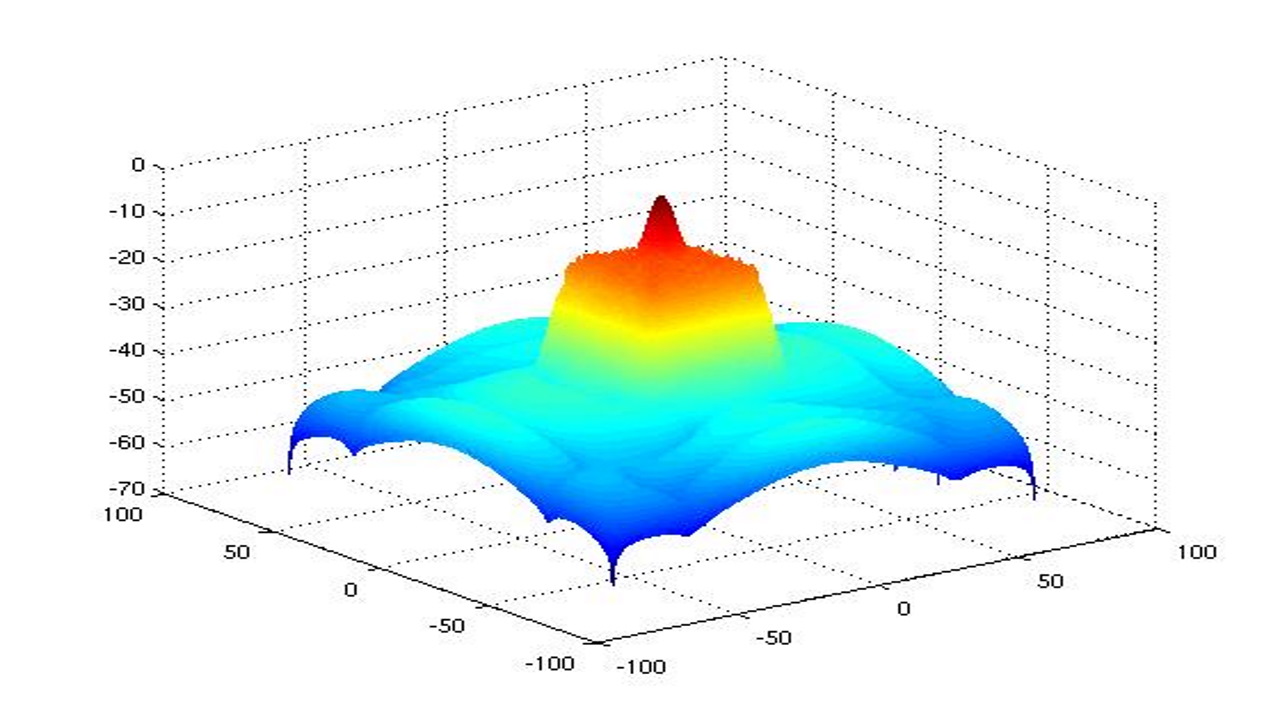
رسم تابع در متلب با دستور surf

دستور surf(X,Y,Z) یک نمودار سه بعدی رسم می‌کند. در این دستور ورودی z به عنوان تابعی از x و y تعریف می‌شود. رنگ در راستای z براساس ارتفاع در این راستا تغییر می‌کند.

مثال دستور surf

سه ماتریس هم اندازه تولید کرده و با استفاده از دستور surf آن را رسم کنید.

[X,Y] = meshgrid(1:0.5:10,1:20);
Z = sin(X) + cos(Y);
surf(X,Y,Z)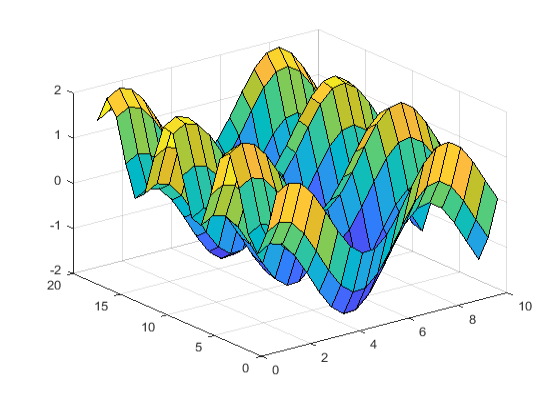

رنگ یک نمودار سه بُعدی که با دستور surf ساخته می‌شود را می‌توان با یک ماتریس چهارم در دستور به عنوان ورودی مشخص کرد. در مثال زیر ماتریس چهارمی را تعریف کرده و رنگ آن را توسط نقشه رنگی یا colormap مشخص کنید، در colormap از یک تک عدد به عنوان شماره رنگ در طیف رنگی استفاده می‌شود. دستور surf از z  به عنوان ارتفاع نمودار و از c به عنوان رنگ نمودار استفاده می‌کند و اندازه c و z یکسان است.

[X,Y] = meshgrid(1:0.5:10,1:20);
Z = sin(X) + cos(Y);
C = X.*Y;
surf(X,Y,Z,C)
colorbar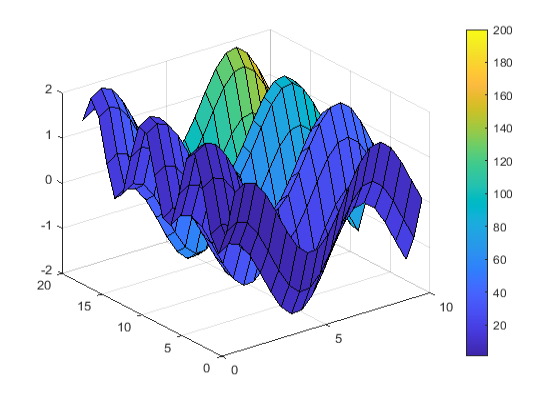

رسم تابع در متلب با دستور fimplicit3

دستور fimplicit3(f) یک تابع سه بعدی که با $$f(x,y,z)=0$$ مشخص می‌شود را رسم می‌کند. بازه رسم این نمودار به صورت پیش فرض بین $$-5$$ تا $$5$$ است.

مثال دستور fimplicit3

تابع هایپربولیک $$x^{2}+y^{2}+z^{2}=0$$ را در بازه پیش فرض $$[-5,5]$$ رسم کنید.

f = @(x,y,z) x.^2 + y.^2 - z.^2;
fimplicit3(f)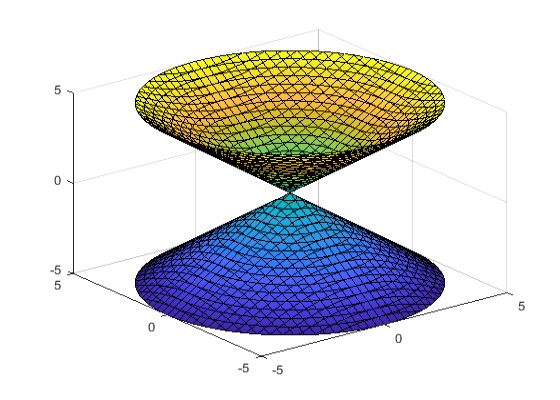

اگر بخواهیم بازه رسم نمودار چیزی غیر از بازه پیش فرض باشد کد را به صورت زیر تغییر می‌دهیم.

f = @(x,y,z) x.^2 + y.^2 - z.^2;
interval = [-5 5 -5 5 0 5];
fimplicit3(f,interval)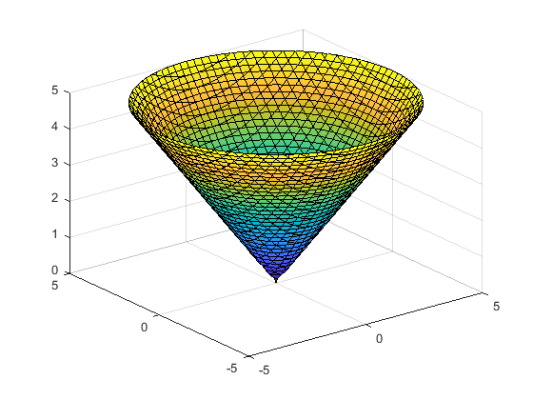

جمع‌بندی

در این مطلب رسم تابع در متلب را آموزش دادیم. به صورت کلی 11 دسته کلی دستور رسم در متلب وجود دارد که با توجه به کاربردهای آن ما در این مطلب دستورهای مربوط به رسم توابع خطی در متلب، دستورهای مربوط به ترسیم پراکندگی داده‌ها در متلب، دستورهای مربوط به نمودارهای داده‌های گسسته، رسم توابع به صورت قطبی و دستورهای مربوط به رسم توابع در سطح و مش‌بندی آن‌ها را بررسی و معرفی کردیم.