دمدولاتور DSBSC — راهنمای جامع

در مطالب قبلی مجله فرادرس به بررسی روش مدولاسیون دامنه و دمدولاسیون دامنه پرداختیم و بیان کردیم که ایراد اساسی روش مدولاسیون حامل کامل باند جانبی مضاعف یا DSBFC این است که حدود ۲/۳ از توان سیگنال در موج حامل قرار دارد و نیز پهنای باند زیادی را اشغال می‌کند. به همین دلیل از روش مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا DSBSC استفاده می‌شود. به مداری که عمل مدولاسیون DSBSC را انجام می‌دهد، مدولاتور DSBSC می‌گویند. فرایند استخراج یک سیگنال پیام اصلی از سیگنال DSBSC دریافت شده در گیرنده، تحت عنوان آشکارسازی DSBSC یا دمدولاسیون DSBSC شناخته می‌شود و به مداری که عمل دمدولاسیون را انجام دهد، دمدولاتور DSBSC می‌گویند. در این مطلب قصد داریم به بررسی انواع دمدولاتورهای DSBSC و نحوه کار آن‌ها بپردازیم.

در حالت کلی می‌توان گفت که دو روش اصلی به عنوان دمدولاتور DSBSC وجود دارند که برای دمدولاتور DSBSC یا آشکارسازی سیگنال DSBSC مورد استفاده قرار می‌گیرند. این دو دمدولاتور عبارتند از:

1. آشکارساز همدوس (Coherent Detector)
2. حلقه کاستاس (Costas Loop)

دمدولاتور DSBSC آشکارساز همدوس

در این نوع از دمدولاسیون DSBSC، برای آشکارسازی سیگنال پیام، از همان سیگنال حاملی استفاده می‌شود که موج DSBSC اصلی را تولید کرده است. به همین دلیل این نوع از آشکارسازی را همدوس (Coherent) یا سنکرون (Synchronous) می‌نامند.

فیلم آموزش مخابرات ۱ – مقدماتی

اینجا کلیک کنید

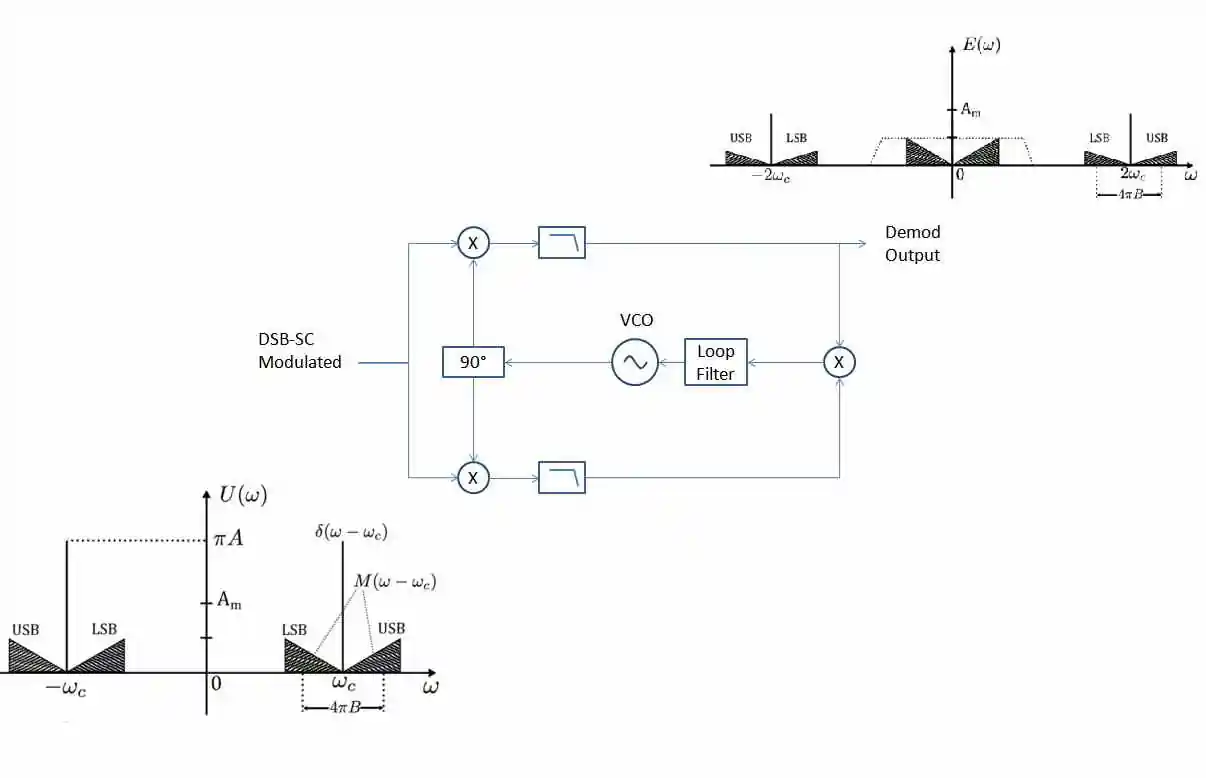
در تصویر زیر بلوک دیاگرام مربوط به روش آشکارساز همدوس نشان داده شده است.

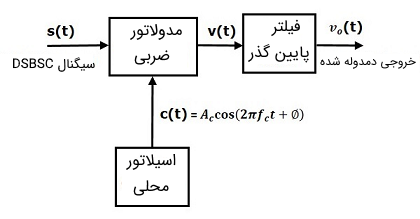
با دقت در تصویر بالا متوجه می‌شویم که برای استخراج سیگنال پیام از سیگنال مدولاسیون DSBSC، باید این سیگنال را در سیگنال حامل ضرب کنیم. البته نکته مهمی که در این مدار وجود دارد این است که سیگنال حامل در مدار دمدولاتور DSBSC، باید دقیقا دارای فرکانس و فاز برابر با فرکانس و فاز سیگنال حامل اصلی باشد که در مدار مدولاتور DSBSC مورد استفاده قرار گرفته است. در مرحله بعد، سیگنالی که از ضرب این دو موج به دست می‌آید را از یک فیلتر پایین گذر عبور می‌دهیم. حال خروجی مدار فیلتر پایین گذر، دقیقا همان سیگنال پیام اصلی است که به دنبال آشکارسازی آن بودیم.

بیان ریاضی دمدولاتور DSBSC آشکارساز همدوس

فرض کنید که سیگنال DSBSC با معادله زیر نشان داده شود:

$$ s \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) m \left ( t \right ) $$

خروجی مربوط به مدار اسیلاتور محلی را نیز می‌توان توسط معادله زیر توصیف کرد:

$$ c \left ( t \right ) = A _ c \cos\left ( 2 \pi f _ c t + \phi \right ) $$

در رابطه فوق، $$ \phi $$ برابر با اختلاف فاز بین سیگنال حاصل از اسیلاتور محلی و سیگنال حاملی در نظر گرفته می‌شود که جهت تولید سیگنال مدولاسیون DSBSC مورد استفاده قرار گرفته است. با توجه به شکل، می‌توان خروجی مدولاتور ضرب‌کننده (که دو سیگنال DSBSC و سیگنال حامل را در هم ضرب می‌کند.) را به صورت زیر نوشت:

$$ v \left ( t \right ) = s \left ( t \right ) c \left ( t \right ) $$

حال مقادیر $$ s \left ( t \right ) $$ و $$ c \left ( t \right ) $$ را در رابطه بالا جایگذاری می‌کنیم و نتیجه را به صورت زیر می‌نویسیم:

$$ \Rightarrow v \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) m \left ( t \right ) A _ c \cos \left ( 2 \pi f _ c t + \phi \right ) $$

$$ = { A _ { c } } ^ { 2 } \cos \left ( 2 \pi f _ c t \right ) \cos \left ( 2 \pi f _ c t + \phi \right ) m \left ( t \right ) $$

$$ = \frac { { A _ { c } } ^ { 2 } } { 2 } \left [ \cos \left ( 4 \pi f _ c t + \phi \right ) + \cos \phi \right ] m \left ( t \right ) $$

$$ v \left ( t \right ) = \frac { { A _ { c } } ^ { 2 } } { 2 } \cos \phi m \left ( t \right ) + \frac { { A _ { c } } ^ { 2 } } { 2 } \cos \left ( 4 \pi f _ c t + \phi \right ) m \left ( t \right ) $$

در معادله به دست آمده در بالا، اولین عبارت برابر با سیگنال پیام اصلی است که قصد آشکارسازی آن را داشتیم. این عبارت را می‌توان از طریق عبور دادن سیگنال فوق از یک فیلتر پایین گذر به دست آورد. بنابراین، خروجی فیلتر پایین گذر به صورت زیر به دست می‌آید:

$$ v _ 0 t = \frac { { A _ { c } } ^ { 2 } } { 2 } \cos \phi m \left ( t \right ) $$

دامنه سیگنال دمدوله شده (Demodulated Signal) زمانی بیشینه می‌شود که مقدار $$ \phi $$ برابر با صفر درجه باشد. دقیقا به همین دلیل است که در ابتدا ذکر کردیم که دو سیگنال اسیلاتور محلی و سیگنال حامل باید در یک فاز باشند. به عبارت دیگر، بین این دو سیگنال نباید هیچ اختلاف فازی وجود داشته باشد.

دامنه سیگنال آشکارسازی شده یا دمدوله شده زمانی برابر با صفر می‌شود که دو سیگنال اسیلاتور محلی و سیگنال حامل دارای ۹۰ درجه اختلاف فاز باشند، به عبارت دیگر، باید $$ \phi = \pm 90 ^ 0 $$ باشد. این پدیده را اثر خنثی تربیعی (Quadrature Null Effect) می‌گویند.

دمدولاتور DSBSC حلقه کاستاس

حلقه کاستاس را می‌توان یک مدار بر پایه حلقه قفل فاز یا PLL دانست که به منظور بازیابی فرکانس سیگنال حامل در سیگنال‌های مدولاسیون حامل سرکوب شده باند جانبی مضاعف یا DSBSC و نیز در سیگنال‌های مدولاسیون فاز (Phase Modulation) مانند BPSK و QPSK مورد استفاده قرار می‌گیرد. این مدار در سال ۱۹۵۰ توسط فردی به نام جان کاستاس (John Costas) در شرکت جنرال الکتریک اختراع گردید. اختراع مدار حلقه کاستاس یکی از عمیق‌ترین و تاثیرگذارترین اختراعات در مخابرات دیجیتال مدرن محسوب می‌شود.

فیلم آموزش مخابرات ۱ – مقدماتی

اینجا کلیک کنید

حلقه کاستاس به منظور هم فاز کردن سیگنال‌های حاصل از اسیلاتور محلی و نیز سیگنال حامل مورد استفاده در مدولاسیون DSBSC به کار گرفته می‌شود. در تصویر زیر یک نمایش بلوک دیاگرامی از مدار حلقه کاستاس نشان داده شده است.

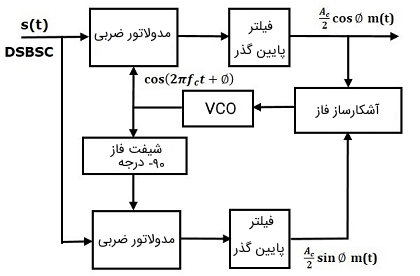
حلقه کاستاس که در شکل بالا نشان دیده می‌شود، از دو مدولاتور ضرب کننده تشکیل شده است. این دو مدولاتور ضرب کننده، یک ورودی مشترک $$ s \left ( t \right ) $$ دارند که همان موج DSBSC است. ورودی‌های دیگر مربوط به دو مدولاتور ضرب کننده، از یک اسیلاتور کنترل شده با ولتاژ (Voltage Controlled Oscillator) یا VCO گرفته می‌شوند. همان طور که در شکل بالا نیز دیده می‌شود، سیگنال حاصل از اسیلاتور کنترل شده با ولتاژ، دارای 90- درجه اختلاف فاز نسبت به سیگنال یکی از مدولاتورهای ضربی است.

بیان ریاضی دمدولاتور DSBSC حلقه کاستاس

از قبل می‌دانیم که معادله مربوط به یک موج مدولاسیون DSBSC را می‌توان به صورت زیر نوشت:

$$ s \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) m \left ( t \right ) $$

حال می‌توانیم معادله سیگنال خروجی از اسیلاتور کنترل شده با ولتاژ را به صورت زیر بیان کنیم:

$$ c _ 1 \left ( t \right ) = \cos \left ( 2 \pi f _ c t + \phi \right ) $$

این خروجی از اسیلاتور کنترل شده با ولتاژ را به عنوان ورودی حامل به مدولاتور ضرب کننده بالایی اعمال می‌کنیم. در نتیجه، سیگنال خروجی از مدار مدولاتور ضرب کننده بالایی به صورت زیر به دست می‌آید:

$$ v _ 1 \left ( t \right ) = s \left ( t \right ) c _ 1 \left ( t \right ) $$

حال با جایگذاری مقادیر $$ s \left ( t \right ) $$ و $$ c _ 1 \left ( t \right ) $$ در معادله بالا، به رابطه زیر دست می‌یابیم:

$$ \Rightarrow v _ 1 \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) m \left ( t \right ) \cos \left ( 2 \pi f _ c t + \phi \right ) $$

پس از ساده‌سازی عبارت بالا، مقدار $$ v _ 1 \left ( t \right ) $$ را به صورت زیر به دست می‌آوریم:

$$ v _ 1 \left ( t \right ) = \frac { A _ c } { 2 } \cos \phi m \left ( t \right ) + \frac { A _ c } { 2 } \cos \left ( 4 \pi f _ c t + \phi \right ) m \left ( t \right ) $$

این سیگنال به عنوان ورودی به فیلتر پایین گذر بالایی اعمال می‌شود. خروجی این فیلتر پایین گذر برابر است با:

$$ v _ { 0 1 } \left ( t \right ) = \frac { A _ c } { 2 } \cos \phi m\left ( t \right ) $$

بنابراین خروجی این فیلتر پایین گذر، نسخه مقیاس شده از سیگنال مدوله شده محسوب می‌شود. خروجی مدار شیفت فاز 90- درجه به صورت زیر محاسبه می‌شود:

$$ c _ 2 \left ( t \right ) = cos \left ( 2 \pi f _ c t + \phi - 9 0 ^ 0 \right ) = \sin \left ( 2 \pi f _ c t + \phi \right ) $$

این سیگنال به عنوان موج حامل به ورودی مدولاتور ضرب کننده پایینی اعمال می‌شود:

$$ v _ 2 \left ( t \right ) = s \left ( t \right ) c _ 2 \left ( t \right ) $$

حال با جایگذاری مقادیر $$ s \left ( t \right ) $$ و $$ c _ 2 \left ( t \right ) $$ در معادله بالا، به رابطه زیر برای $$ v _ 2 \left ( t \right ) $$ می‌رسیم:

$$ \Rightarrow v _ 2 \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) m \left ( t \right ) \sin \left ( 2 \pi f _ c t + \phi \right ) $$

حال بعد از ساده‌سازی معادله فوق، مقدار  $$ v _ 2 \left ( t \right ) $$ به صورت زیر به دست می آید:

$$ v _ 2 \left ( t \right ) = \frac { A _ c } { 2 } \sin \phi m \left ( t \right ) + \frac { A _ c } { 2 } \sin \left ( 4 \pi f _ c t + \phi \right ) m \left ( t \right ) $$

این سیگنال نیز به عنوان ورودی به فیلتر پایین گذر پایینی اعمال می‌شود. بنابراین خروجی فیلتر پایین گذر پایین به صورت زیر به دست می‌آید:

$$ v _ { 0 2 } \left ( t \right ) = \frac { A _ c } { 2 } \sin \phi m \left ( t \right ) $$

خروجی فیلتر پایین گذر پایینی با خروجی مدار فیلتر پایین گذر بالایی، به اندازه 90- درجه اختلاف فاز دارد. حال خروجی‌های این دو فیلتر پایین گذر به عنوان ورودی به مدار آشکارساز فاز (Phase Discriminator) اعمال می‌شوند. بر اساس اختلاف فاز بین این دو سیگنال، آشکارساز فاز یک سیگنال کنترل DC تولید می‌کند.

این سیگنال به عنوان ورودی به مدار اسیلاتور کنترل شده با ولتاژ یا VCO داده می‌شود تا مقدار خطای فاز (Phase Error) موجود در سیگنال خروجی VCO را تصحیح کند. بنابراین سیگنال حاملی که برای تولید سیگنال مدولاسیون DSBSC مورد استفاده قرار می‌گیرد و سیگنال حاصل از اسیلاتور کنترل شده با ولتاژ که به صورت محلی تولید می‌شود، با یکدیگر در یک فاز قرار دارند.

اگر این مطلب برای شما مفید بوده است، مطالب و آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌های مهندسی برق
• آموزش الکترونیک ۱
• اشمیت تریگر با اپ امپ — از صفر تا صد
• نسبت سیگنال به نویز چیست؟ — از صفر تا صد
• تبدیل موجک — از صفر تا صد

^^