دستگاه معادلات دیفرانسیل ناهمگن با ضرایب ثابت – از صفر تا صد

در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. همچنین، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. در این آموزش دستگاه معادلات ناهمگن خطی را معرفی و برخی از روش‌های حل آن را بیان می‌کنیم.

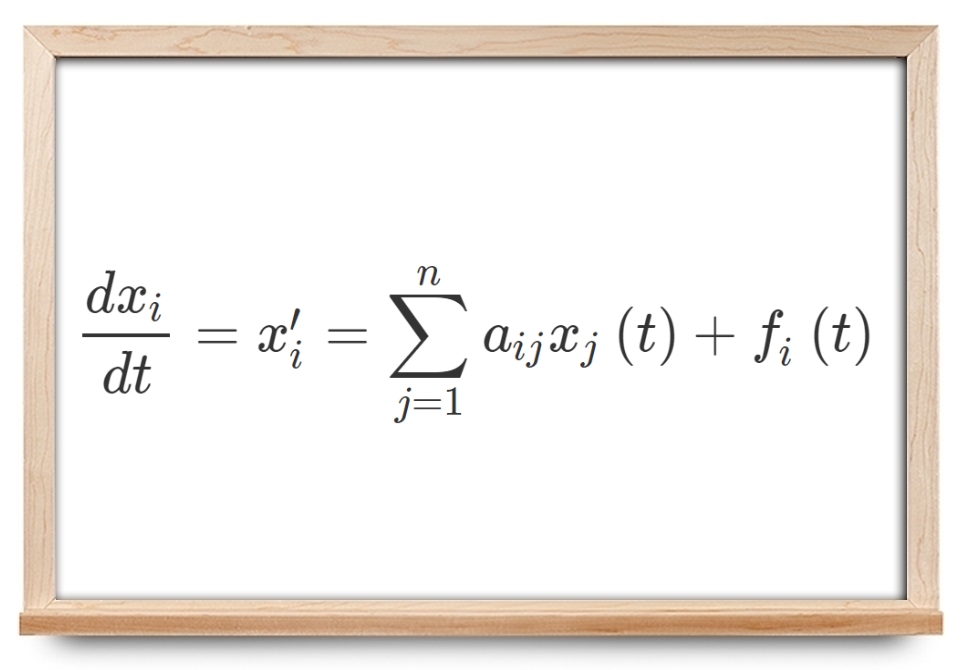
یک دستگاه ناهمگن خطی معمولی شامل $$n$$ معادله با ضرایب ثابت را می‌توان به صورت زیر نوشت:

$$\large { \frac { { d { x _ i } } } { { d t } } = { x ’ _ i } } = { \sum \limits _ { j = 1 } ^ n { { a _ { i j } } { x _ j } \left ( t \right ) } + { f _ i } \left ( t \right ) , \; \; } \kern-0.3pt { i = 1 , 2 , \ldots , n }$$

که در آن $$t$$ یک متغیر مستقل (اغلب زمان)، $$x_i(t)$$ توابع نامعلوم پیوسته و مشتق‌پذیر در بازه حقیقی $$\left[ {a,b} \right]$$ روی محور $$t$$، $${a_{ij}}\left( {i,j = 1, \ldots ,n} \right)$$ ضرایب ثابت و $$f_i(t)$$ توابعی از متغیر مستقل $$t$$ هستند. فرض می‌کنیم توابع $$x_i(t)$$ و $$f_i(t)$$ و ضرایب $$a_{ij}$$ می‌توانند مقادیر حقیقی و مختلط اختیار کنند.

بردارهای زیر را در نظر بگیرید:

$$ \large { \mathbf { X } \left ( t \right ) = \left[ { \begin {array} { * { 2 0 } { c } }<br /> { { x _ 1 } \left ( t \right ) } \\<br /> { { x _ 2 } \left ( t \right ) } \\<br /> \vdots \\<br /> { { x _ n } \left ( t \right ) }<br /> \end {array} } \right] , \; \; } \kern0pt<br /> { \mathbf { f } \left ( t \right ) = \left[ { \begin {array} {*{20}{c}}<br /> { { f _ 1 } \left ( t \right ) } \\<br /> { { f _ 2 }\left ( t \right ) } \\<br /> \vdots \\<br /> { { f _ n } \left ( t \right ) }<br /> \end {array}} \right] } $$

همچنین ماتریس زیر را تعریف می‌کنیم:

$$ \large A = \left[ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ { 1 1 } } } & {{ a _ { 1 2 } } } & \vdots & { { a _ { 1 n } } }\\<br /> { {a _ { 2 1 } } } & {{ a_ { 2 2 } } } & \vdots & { { a _ { 2 n} } } \\<br /> \cdots & \cdots & \cdots & \cdots \\<br /> { { a _ { n 1 } } }& { {a _ { n 2 } } } & \vdots & { { a _ { n n } }}<br /> \end{array}} \right]. $$

آن‌گاه دستگاه معادلات را می‌توان به فرم فشرده ماتریسی زیر نوشت:

$$\large \mathbf { X } ’ \left ( t \right ) = A \mathbf { X } \left ( t \right ) + \mathbf { f } \left ( t \right ) .$$

مشابه دستگاه معادلات دیفرانسیل خطی همگن، قضیه زیر برای دستگاه معادلات غیرهمگن برقرار است.

قضیه: جواب عمومی $$\mathbf{X}\left( t \right)$$ دستگاه ناهمگن، برابر با مجموع جواب عمومی $${\mathbf{X}_0}\left( t \right)$$ متناظر با دستگاه همگن و یک جواب خصوصی $${\mathbf{X}_1}\left( t \right)$$ دستگاه ناهمگن است:

$$\large \mathbf { X } \left ( t \right ) = { \mathbf { X } _ 0 } \left ( t \right ) + { \mathbf { X} _ 1 } \left ( t \right ) .$$

در آموزش‌های پیشین مجله فرادرس، روش‌های حل دستگاه همگن را بیان کردیم. بنابراین، در اینجا به روش یافتن جواب خصوصی می‌پردازیم.

یک ویژگی مهم دیگر از دستگاه ناهمگن خطی، اصل برهم‌نهی یا جمع آثار است که به صورت زیر بیان می‌شود:

اگر $${\mathbf{X}_1}\left( t \right)$$ یک جواب برای دستگاهی با بخش ناهمگن $${\mathbf{f}_1}\left( t \right)$$، و $${\mathbf{X}_2}\left( t \right)$$ جواب همان دستگاه با بخش ناهمگن $${\mathbf{f}_2}\left( t \right)$$ باشد، آن‌گاه تابع برداریِ

$$\large \mathbf { X } \left ( t \right ) = { \mathbf { X } _ 1 } \left ( t \right ) + { \mathbf { X } _ 2 } \left ( t \right )$$

یک جواب برای دستگاه با بخش ناهمگن زیر است:

$$\large \mathbf { f } \left ( t \right ) = { \mathbf { f } _ 1 } \left ( t \right ) + { \mathbf { f } _ 2 } \left ( t \right ) .$$

روش‌های حل دستگاه معادلات ناهمگن خطی  با ضرایب ثابت

متداول‌ترین روش‌های حل دستگاه‌های ناهمگن، روش حذفی، روش ضرایب نامعین (در حالتی که $$\mathbf{f}\left( t \right)$$ یک بردار شبه‌چندجمله‌ای است) و روش تغییر پارامتر هستند. در ادامه، این روش‌ها را بررسی می‌کنیم.

روش حذفی

با استفاده از این روش می‌توان یک دستگاه ناهمگن خطی معمولی شامل $$n$$ معادله با ضرایب ثابت را با یک معادله مرتبه $$n$$ کاهش داد. این روش برای حل دستگاه‌های مرتبه دوم مفید است.

روش ضرایب نامعین

روش ضرایب نامعین برای حل دستگاه‌ معادلاتی که بخش ناهمگن آن‌ها یک شبه‌چندجمله‌ای است، کاربرد دارد.

یک شبه‌چندجمله‌ای برداری حقیقی، تابعی برداری به فرم زیر است:

$$\large { \mathbf { f } \left ( t \right ) } = { { e ^ { \alpha t }} \left[ { \cos \left ( { \beta t } \right ) { \mathbf { P } _ m } \left ( t \right ) } \right . } + { \left . { \sin \left ( { \beta t } \right ){ \mathbf { Q } _ m } \left ( t \right ) } \right] }$$

که در آن $$\alpha$$ و $$\beta$$ اعدادی حقیقی و $${{\mathbf{P}_m}\left( t \right)}$$ و $${{\mathbf{Q}_m}\left( t \right)}$$ چندجمله‌ای‌های برداری درجه $$m$$ هستند. برای مثال، چندجمله‌ای برداری $${{\mathbf{P}_m}\left( t \right)}$$ به صورت زیر نوشته می‌شود:

$$\large { { \mathbf { P } _ m } \left ( t \right ) } = { { \mathbf { A } _ 0 } + { \mathbf { A } _ 1 } t + { \mathbf { A } _ 2 } { t ^ 2 } + \cdots } + { { \mathbf { A } _ m } { t ^ m } }$$

که در آن $${\mathbf{A}_0}$$، $${\mathbf{A}_2}$$، $$\ldots$$ و $${\mathbf{A}_m}$$ بردارهایی به طول $$n$$ هستند ($$n$$ تعداد معادلات دستگاه است).

در حالتی که بخش ناهمگن $$\mathbf{f}\left( t \right)$$، یک شبه‌چندجمله‌ای برداری باشد، جواب عمومی نیز یک شبه‌چندجمله‌ای برداری با ساختار مشابه $$\mathbf{f}\left( t \right)$$ خواهد بود.

برای مثال، اگر تابع ناهمگن به صورت زیر باشد:

$$\large \mathbf { f } \left ( t \right ) = { e ^ { \alpha t } }{ \mathbf { P } _ m } \left ( t \right )$$

جواب خصوصی به فرم زیر خواهد بود:

$$\large { \mathbf { X } _ 1 } \left ( t \right ) = { e ^ { \alpha t } } { \mathbf { P } _ { m + k } } \left ( t \right )$$

که در آن، در حالت غیر رزونانسی، $$k=0$$ است؛ یعنی وقتی اندیس $$\alpha$$ با یک مقدار ویژه $$\lambda _i$$ منطبق باشد، یعنی در حالت رزونانس باشیم، مقدار $$k$$ برابر با طول زنجیره جردن برای مقدار ویژه $$\lambda _i$$ قرار داده می‌شود. در عمل، می‌توان $$k$$ را به‌ عنوان کثرت جبری $$\lambda _i$$ در نظر گرفت.

برای تعیین درجه شبه‌چندجمله‌ای‌های زیر، از قاعده‌های مشابه مربوط به چندجمله‌ای‌ها استفاده می‌شود:

$$\large { { e ^ { \alpha t } } \cos \left ( { \beta t } \right ) , \; \; } \kern0pt { { e ^ { \alpha t } } \sin \left ( { \beta t } \right ) . }$$

در اینجا، حالت رزونانس زمانی رخ می‌دهد که $$\alpha + \beta i$$ با مقدار ویژه مختلط $$\lambda _i$$ ماتریس $$A$$ برابر باشد.

بعد از انتخاب ساختار جواب خصوصی $${\mathbf{X}_1}\left( t \right)$$، ضرایب برداری نامعلوم $${A_0},{A_1}, \ldots ,{A_m}, \ldots ,{A_{m + k}}$$ با جایگزینی عبارت $${\mathbf{X}_1}\left( t \right)$$ در دستگاه اصلی و برابر قرار دادن ضرایب جملات برای توان‌های یکسان $$t$$ به دست می‌آید.

روش تغییر ضرایب

روش تغییر ضرایب (روش لاگرانژ) یک روش رایج برای حل دستگاه با تابع دلخواه $$\mathbf{f}\left( t \right)$$ در سمت راست آن است.

فرض کنید جواب عمومی دستگاه همگن محاسبه شده و به صورت زیر است:

$$\large { \mathbf { X } _ 0 } \left ( t \right ) = \Phi \left ( t \right ) \mathbf { C }$$

که در آن $$\Phi \left( t \right)$$ یک دستگاه اساسی از جواب‌ها است؛ یعنی ماتریسی با اندازه $$n \times n$$ که ستون‌های آن، جواب‌های مستقل خطی دستگاه همگن  هستند و $${\left( {{C_1},{C_2}, \ldots ,{C_n}} \right)^T}$$ بردار اعداد ثابت دلخواه $${C_i}\left( {i = 1, \ldots ,n} \right)$$‌ است.

ثابت‌های $${C_i}$$ را با توابع نامعلوم $$C_i (t)$$ جایگزین کرده و تابع $$\mathbf{X}\left( t \right) = \Phi \left( t \right)\mathbf{C}\left( t \right)$$ را در دستگاه معادلات ناهمگن قرار می‌دهیم:

$$ \large \require {cancel}<br /> { \mathbf { X ’ } \left ( t \right ) = A \mathbf { X } \left ( t \right ) + \mathbf { f } \left ( t \right ) , \; \; } \Rightarrow<br /> { \cancel { \Phi ’ \left ( t \right ) \mathbf { C } \left ( t \right ) } + \Phi \left ( t \right ) \mathbf { C ’ } \left ( t \right )} $$

$$\large = { \cancel { A \Phi \left ( t \right ) \mathbf { C } \left ( t \right ) } + \mathbf { f } \left ( t \right ) , \; \; } \Rightarrow { \Phi \left ( t \right ) \mathbf { C ’ } \left ( t \right ) = \mathbf { f } \left ( t \right ) . }$$

از آن‌جایی که رونسکین دستگاه، صفر نیست، ماتریس معکوس $${\Phi ^{ – 1}}\left( t \right)$$ وجود دارد. با ضرب $${\Phi ^{ – 1}}\left( t \right)$$ در سمت چپ معادله آخر، داریم:

$$\large { { { \Phi ^ { – 1 } } \left ( t \right ) \Phi \left ( t \right ) \mathbf { C ’ } \left ( t \right ) } = { { \Phi ^ { – 1 } } \left ( t \right ) \mathbf { f } \left ( t \right ) , \; \; } }\\ \large \Rightarrow { \mathbf { C ’ } \left ( t \right ) = { \Phi ^ { – 1 } } \left ( t \right ) \mathbf { f } \left ( t \right ) , \; \; } \Rightarrow { { \mathbf { C } \left ( t \right ) = { \mathbf { C } _ 0 } } + { \int { { \Phi ^ { – 1 } } \left ( t \right ) \mathbf { f } \left ( t \right ) d t } } }$$

که در آن، $${\mathbf{C}_0}$$ یک بردار ثابت دلخواه است.

در نتیجه، جواب عمومی دستگاه ناهمگن را می‌توان به صورت زیر نوشت:

$$\large { \mathbf { X } \left ( t \right ) = \Phi \left ( t \right ) \mathbf { C } \left ( t \right ) } = { { \Phi \left ( t \right ) { \mathbf { C } _ 0 } } + { \Phi \left ( t \right ) \int { { \Phi ^ { – 1 } } \left ( t \right ) \mathbf { f } \left ( t \right ) d t } } } = { { \mathbf { X } _ 0 } \left ( t \right ) + { \mathbf { X } _ 1 } \left ( t \right ) . }$$

یک جواب خصوصی برای معادل ناهمگن، به صورت زیر است:

$$\large { { \mathbf { X } _ 1 } \left ( t \right ) } = { \Phi \left ( t \right ) \int { { \Phi ^ { – 1 } } \left ( t \right ) \mathbf { f } \left ( t \right ) d t } . }$$

بنابراین، جواب معادله همگن را می‌توان با محاسبه انتگرال برای هر جمله ناهمگن $$\mathbf{f}\left( t \right)$$ به دست آورد. در بسیاری از مسائل، انتگرال‌های متناظر را می‌توان به صورت تحلیلی محاسبه کرد. با این کار، بیان جواب دستگاه ناهمگن به صورت صریح ممکن است.

مثال‌ها

در ادامه، چند مثال را بررسی می‌کنیم.

مثال ۱

دستگاه معادلات زیر را با روش حذفی حل کنید:

$$\large { x ’ = x + 2 y + { e ^ { – 2 t } } , \; \; } \kern-0.3pt { y ’ = 4 x – y . }$$

حل: از معادله اول مشتق می‌گیریم و $$y’$$ معادله دوم را در آن قرار می‌دهیم:

$$\large { x ^ { \prime \prime } = x ’ + 2 y ’ + 2 { e ^ { – 2 t } } , \; \; } \Rightarrow { x ^ { \prime \prime } = x ’ + 2 \left ( { 4 x – y } \right ) – 2 { e ^ { – 2 t } } , \; \; } \\ \large \Rightarrow { x ^ { \prime \prime } = x ’ + 8 x – 2 y – 2 { e ^ { – 2 t } } . }$$

همچنین می‌توانیم معادله اول را برای $$2y$$ حل کرده و در معادله اخیر قرار دهیم:

$$\large { 2 y = x ’ – x – { e ^ { – 2 t } } , \; \; } \Rightarrow { { x ^ { \prime \prime } = x ’ + 8 x } - { \left ( { x ’ – x – { e ^ { – 2 t } } } \right ) } - { 2 { e ^ { – 2 t } } , \; \; } } \\ \large \Rightarrow { { x ^ { \prime \prime } = x ’ + 8 x } - { x ’ + x } + { { e ^ { – 2 t } } – 2 { e ^ { – 2 t } } , \; \; } } \Rightarrow { x ^ { \prime \prime } – 9 x = – { e ^ { – 2 t } } . }$$

همان‌طور که می‌بینیم، یک معادله همگن خطی مرتبه دوم برای تابع $$x(t)$$ داریم.

ابتدا معادله همگن را حل می‌کنیم:

$$\large x^{\prime\prime} – 9x = 0.$$

ریشه‌های معادله کمکی برابرند با:

$$\large {{\lambda ^2} – 9 = 0,\;\; }\Rightarrow {{\lambda _{1,2}} = \pm 3.}$$

جواب معادله همگن برای $$x(t)$$ به صورت زیر است:

$$\large { x _ 0 } \left ( t \right ) = { C _ 1 } { e ^ { 3 t } } + { C _ 2 } { e ^ { – 3 t } }$$

که در آن $$C_1$$ و $$C_2$$ اعداد دلخواهی هستند.

با توجه جمله ناهمگن در معادله $$x(t)$$، جواب خصوصی $$x_1(t)$$ به فرم زیر خواهد بود:

$$\large { x _ 1 } \left ( t \right ) = A { e ^ { – 2 t } } .$$

با جایگذاری این جواب در معادله ناهمگن، ضریب $$A$$ را تعیین می‌کنیم:

$$\large { { \left ( { – 2 } \right ) ^ 2 } A { e ^ { – 2 t } } – 9 A { e ^ { – 2 t } } = – { e ^ { – 2 t } } , \; \; }\\ \large \Rightarrow { 4 A – 9 A = – 1 , \; \; } \Rightarrow { 5 A = 1 , \; \; } \Rightarrow { A = \frac { 1 } { 5 } . }$$

بنابراین، جواب $$x_1(t)$$ برابر است با:

$$\large {x_1}\left( t \right) = \frac{1}{5}{e^{ – 2t}}.$$

در نتیجه، جواب معادله را می‌توان به صورت زیر نوشت:‌

$$\large { x \left ( t \right ) = { x _ 0 } \left ( t \right ) + { x _ 1 } \left ( t \right ) } = { { C _ 1 } { e ^ { 3 t } } + { C _ 2 } { e ^ { – 3 t } } + \frac { 1 } { 5 } { e ^ { – 2 t } } .}$$

اکنون باید تابع $$y(t)$$ را پیدا کنیم. برای این کار، $$x’\left( t \right)$$ را محاسبه و در معادله اول دستگاه اصلی قرار می‌دهیم:‌

$$\large { { x ’ \left ( t \right ) = 3 { C _ 1 } { e ^ {3 t } } } - { 3 { C _ 2 } { e ^ { – 3 t } } – \frac { 2 } { 5 } { e ^ { – 2 t} } , \; \; } } \\ \large \Rightarrow { { 3 { C _ 1 } { e ^ { 3 t } } – 3 { C _ 2 } { e ^ { – 3 t } } – \frac { 2 } { 5 } { e ^ { – 2 t } } } = { { C _ 1 } { e ^ { 3 t } } + { C _ 2 } { e ^ { – 3 t } } } + { \frac { 1 } { 5 } { e ^ { – 2 t } } + 2 y + { e ^ { – 2 t } } , \; \; } } \\ \large \Rightarrow { 2 y = 2 { C _ 1 } {e ^ { 3 t } } – 4 { C _ 2 } { e ^ { – 3 t } } – \frac { 7 } { 5 } { e ^ { – 2 t } } , \; \; } \\ \large \Rightarrow { { y \left ( t \right ) = { C _ 1 } { e ^ { 3 t } } – 2 { C _ 2 }{ e ^ { – 3 t } } } - { \frac { 7 } { { 1 0 } } { e ^ { – 2 t } } . } }$$

جواب نهایی به صورت زیر است:

$$\large \left\{ \begin {array} {l} { x \left ( t \right ) = { C _ 1 } { e ^ { 3 t } } } + { { C _ 2 }{ e ^ { – 3 t } } } + { \frac { 1 } { 5 } { e ^ { – 2 t } } } \\ { y \left ( t \right ) = { C _ 1 } { e ^ { 3 t } } } - { 2 { C _ 2 } { e ^ { – 3 t } } } - { \frac { 7 } { { 1 0 } } { e ^ { – 2 t } } } \end {array} \right . .$$

مثال ۲

جواب دستگاه معادلات زیر را با استفاده از روش ضرایب نامعین به دست آورید:

$$\large { \frac { { d x } } { { d t } } = 2 x + y , \; \; } \kern-0.3pt { \frac { { d y } } { { d t } } = 3 y + t { e ^ t } . }$$

حل:‌ دستگاه معادلات را به فرم ماتریسی زیر می‌نویسیم:

$$\large { \mathbf { X } ’ \left ( t \right ) = A \mathbf { X } \left ( t \right ) + \mathbf { f } \left ( t \right ) }$$

که در آن:

$$ \large { \mathbf { X } \left ( t \right ) = \left[ { \begin {array} { * { 2 0} { c } }<br /> { x \left ( t \right ) } \\<br /> { y \left ( t \right ) }<br /> \end {array}} \right] , \; \; } \kern-0.3pt<br /> { A = \left[ { \begin {array} { * { 2 0 } { c } }<br /> 2 & 1 \\<br /> 0 & 3<br /> \end {array} } \right] , \; \; } \kern-0.3pt<br /> { \mathbf { f } \left ( t \right ) = \left[ { \begin {array} { * { 2 0 } { c } }<br /> 0 \\<br /> { t { e ^ t } }<br /> \end {array}} \right] . } $$

ابتدا جواب همگن سیستم را تعیین می‌کنیم. مقادیر ویژه ماتریس $$A$$ برابرند با:

$$ \large { { \det \left ( {A – \lambda I } \right ) } = { \left | { \begin {array} { * { 2 0 } { c } }<br /> { 2 – \lambda } & 1 \\<br /> 0 & { 3 – \lambda }<br /> \end {array}} \right | = 0 , \; \; } } \\ \large \Rightarrow<br /> { \left ( { 2 – \lambda } \right ) \left ( { 3 – \lambda } \right ) = 0 , \; \; } \Rightarrow<br /> { { \lambda _ 1 } = 2 , \; { \lambda _ 2 } = 3 . } $$

اکنون بردار ویژه $${\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T}$$ مناظر با مقدار ویژه $${\lambda _1} = 2$$ را به دست می‌آوریم:

$$ \large { \left ( { A – { \lambda _ 1 } I } \right ){ \mathbf { V } _ 1 } = \mathbf { 0 } , \; \; } \Rightarrow<br /> { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { 2 – 2 } & 1 \\<br /> 0 & { 3 – 2 }<br /> \end {array} } \right ] \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 1 } } } \\<br /> { { V _ { 2 1 } } }<br /> \end {array} } \right ] = \mathbf { 0 } , \; \; } \\ \large \Rightarrow<br /> { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 0 & 1 \\<br /> 0 & 1<br /> \end {array} } \right ] \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 1 } } } \\<br /> { { V _ { 2 1 } } }<br /> \end {array} } \right ] = \mathbf { 0 } , \; \; } \Rightarrow<br /> { 0 \cdot { V _ { 1 1 } } + 1 \cdot { V _ { 2 1 } } = 0 . } $$

همان‌طور که می‌بینیم، $${V_{21}} = 0$$ و مقدار $$V_{11}$$ عددی دلخواه خواهد بود. برای سادگی، مقدار $${V_{11}} = 1$$ را انتخاب می‌کنیم. بنابراین، داریم: $${\mathbf{V}_1} = {\left( {1,0} \right)^T}$$.

به طور مشابه، بردار ویژه $${\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T}$$ متناظر با مقدار ویژه $${\lambda _2} = 3$$ را محاسبه می‌کنیم:

$$ \large { \left ( { A – { \lambda _ 2 } I } \right ){ \mathbf { V } _ 2 } = \mathbf { 0 } , \; \; } \Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> { 2 – 3 } & 1 \\<br /> 0 & { 3 – 3 }<br /> \end {array} } \right ] \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 2 } } } \\<br /> { { V _ { 2 2 } } }<br /> \end {array} } \right ] = \mathbf { 0 } , \; \; } \\ \large \Rightarrow<br /> { \left [ { \begin {array} { * { 2 0 } { r } }<br /> { - 1 } & 1 \\<br /> 0 & 0<br /> \end {array} } \right ] \left[ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 2 } } } \\<br /> { { V _ { 2 2 } } }<br /> \end {array} } \right ] = \mathbf { 0 } , \; \; } \Rightarrow<br /> { - { V _ { 1 2 } } + { V _ { 2 2 } } = 0 . } $$

با در نظر گرفتن $${V_{22}} = t$$، داریم: $${V_{12}} = {V_{22}} = t$$. در نتیجه:

$$ \large { { \mathbf { V } _ 2 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { V _ { 1 2 } } } \\<br /> { { V _ { 2 2 } } }<br /> \end {array} } \right ] = \left [ { \begin {array} { * { 2 0 } { c } }<br /> t \\<br /> t<br /> \end {array} } \right ] }<br /> = { t \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 \\<br /> 1<br /> \end {array} } \right ] }<br /> \sim { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 \\<br /> 1<br /> \end {array} } \right ] . } $$

در نتیجه، جواب عمومی دستگاه همگن برابر است با:

$$ \large { { \mathbf { X } _ 0 } \left ( t \right ) = \left [ { \begin {array} { * { 2 0 } {c } }<br /> x \\<br /> y<br /> \end {array} } \right ] }<br /> = { { C _ 1 } { e ^ { { \lambda _ 1 } t } } { \mathbf { V } _ 1 } + { C _ 2 } { e ^ { { \lambda _ 2 } t } } { \mathbf { V } _ 2 } }<br /> \\ \large = { { C _ 1 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 \\<br /> 0<br /> \end {array} } \right ] + { C _ 2 } { e ^ { 3 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 \\<br /> 1<br /> \end {array} } \right ] . } $$

اکنون جواب خصوصی $${\mathbf{X}_1}\left( t \right)$$ را محاسبه می‌کنیم. جمله ناهمگن به فرم شبه‌چندجمله‌ای $${\mathbf{P}_1}\left( t \right){e^t}$$ است. درجه تابع نمایی $$\alpha = 1$$ است. از آن‌جایی که این مقدار با هیچ‌ یک از مقادیر ویژه $${\lambda _1} = 2$$ و $${\lambda _2} = 3$$ منطبق نیست، یک جواب خصوصی با فرم مشابه $$\mathbf{f}\left( t \right)$$ محاسبه می‌کنیم؛ یعنی فرض می‌کنیم:

$$ \large { { \mathbf { X } _ 1 } \left ( t \right ) = \left ( { \begin {array} { * { 2 0 } { c } }<br /> { { x _ 1 } \left ( t \right ) } \\<br /> { { y _ 1 } \left ( t \right ) }<br /> \end {array} } \right ) } = { { \mathbf { P } _ 1 } \left ( t \right ) { e ^ t } \; \; } \kern-0.3pt<br /> { \text{,}\;\;}\kern-0.3pt { { \mathbf { P } _ 1 } \left ( t \right ) = { \mathbf { A } _ 0 } + { \mathbf { A } _ 1} t . } $$

اکنون بردارهای مجهول $${\mathbf{A}_0}$$ و $${\mathbf{A}_1}$$ را با استفاده از روش ضرایب نامعین پیدا می‌کنیم:

$$ \large { { \mathbf { A } _ 0 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 0 } } \\<br /> { { b _ 0 } }<br /> \end {array} } \right ] , \; \; } \kern-0.3pt { { \mathbf { A } _ 1 } = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } } \\<br /> { { b _ 1 } }<br /> \end {array} } \right ] . } $$

بنابراین، جواب خصوصی به صورت زیر نوشته می‌شود:

$$ \large { { \mathbf { X } _ 1} \left ( t \right ) = \left[ { \begin {array} { * { 2 0 }{ c }}<br /> { { x _ 1 } \left ( t \right ) } \\<br /> { { y _ 1 } \left( t \right ) }<br /> \end {array} } \right ] }= { \left [ { \begin {array} { * {2 0 } {c } }<br /> { \left ( { { a _ 0 } + { a _ 1} t } \right ) { e ^ t } } \\<br /> { \left ( { { b _ 0 } + { b _1 } t } \right) {e ^ t }}<br /> \end {array}} \right] . } $$

اکنون $${\mathbf{X}_1}\left( t \right)$$ را در معادله ناهمگن اصلی جایگذاری می‌کنیم:

$$ \large { { \mathbf { X ’ } _ 1 } \left ( t \right ) = A { \mathbf { X } _ 1 } \left ( t \right ) + \mathbf { f } \left ( t \right ) , \; \; } \\ \large \Rightarrow<br /> { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 1 } { e ^ t } + \left ( { { a _ 0 } + { a _ 1 } t } \right ) { e ^ t } } \\<br /> { { b _ 1 } { e ^ t } + \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ t } }<br /> \end {array} } \right] }<br /> = { \left [ { \begin {array} { * { 2 0 } { c } }<br /> 2 & 1 \\<br /> 0 & 3<br /> \end {array}} \right] \left [ { \begin {array} { * { 2 0 } { c } }<br /> { \left ( { { a _ 0 } + { a _ 1 } t } \right ) { e ^ t } } \\<br /> { \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ t } }<br /> \end {array} } \right ] + \left [ { \begin {array} { * { 2 0 }{ c } }<br /> 0 \\<br /> { t { e ^ t } }<br /> \end {array} } \right] ,} $$

$$ \large \Rightarrow \kern0pt<br /> { \left \{ { \begin {array} { * { 2 0 } { l } }<br /> { { \left ( { { a _ 1 } + { a _ 0 } + { a _ 1 } t } \right ) { e ^ t } } = { \left ( { 2 { a _ 0 } + 2 { a _ 1 } t } \right ) {e ^ t } } + { \left ( { { b _ 0 } + { b _ 1 } t } \right ) { e ^ t } } } \\<br /> { { \left ( { { b _ 1 } + { b _ 0 } + { b _ 1 } t } \right ) { e ^ t } } = { \left ( { 3 { b _ 0 } + 3 { b _ 1 } t } \right ) { e ^ t } } + { t { e ^ t } } }<br /> \end {array} } \right . } $$

با تقسیم هر دو سمت معادله بر $${{e^t}}$$، خواهیم داشت:‌

$$ \large \left\{ { \begin {array} { * { 2 0 } {l} }<br /> { { { a _ 1 } + { a _ 0 } + { a _ 1 } t } = { 2 { a _ 0 } + 2 { a _ 1 } t + { b _ 0 } + { b _ 1 } t } } \\<br /> { { { b _ 1 } + { b _ 0 } + { b _ 1 } t } = { 3 { b _ 0 } + 3 { b _ 1 } t + t } }<br /> \end {array} } \right . $$

با برابر قرار دادن ضرایب جملات مشابه، دستگاه معادلات زیر را به‌ دست می‌آوریم:

$$\large { \left\{ \begin {array} {l} { a _ 1 } + { a _ 0 } = 2 { a _ 0 } + { b _ 0 } \\ { a _ 1 } = 2 { a _ 1 } + { b _ 1 } \\ { b _ 1 } + { b _ 0 } = 3 { b _ 0 } \\ { b _ 1 } = 3 { b _ 1 } + 1 \end {array} \right.,\;\; }\Rightarrow { \left\{ \begin {array} { l } { a _ 1 } = { a _ 0 } + { b _ 0 } \\ { a _ 1 } + { b _ 1 } = 0 \\ { b _ 1 } = 2 { b _ 0 } \\ 2 { b _ 1 } + 1 = 0 \end {array} \right . . }$$

از دستگاه بالا، ضرایب مجهول محاسبه می‌شود:

$$\large { { b _ 1 } = – \frac { 1 } { 2 } , \; \; } \kern-0.3pt{{b_0} = \frac{{{b_1}}}{2} = – \frac{1}{4},\;\;}\kern-0.3pt { { a _ 1 } = – { b _ 1 } = \frac { 1 } { 2 } , \; \; } \kern-0.3pt \\ \large { { a _ 0 } = { a _ 1 } – { b _ 0 } } = { \frac { 1 } { 2 } – \left ( { – \frac { 1 } {4 } } \right ) } = { \frac { 3 } { 4 } . }$$

بنابراین، جواب خصوصی $${\mathbf{X}_1}\left( t \right)$$ برابر است با:

$$ \large { { \mathbf { X } _ 1 } \left ( t \right) = \left[ { \begin {array} { * { 2 0 } { c } }<br /> { { x _ 1 } \left ( t \right ) } \\<br /> { { y _ 1 } \left ( t \right ) }<br /> \end {array} } \right ] }<br /> = { { \mathbf { P } _ 1 } \left ( t \right) { e ^ t }<br /> = \left [ { \begin {array} { * { 2 0 } { c } }<br /> { { a _ 0 } + { a _ 1 } t } \\<br /> { { b _ 0 } + { b _ 1 } t }<br /> \end {array} } \right] { e ^ t } } \\ \large<br /> = { \left [ { \begin {array} { * { 2 0 } { c } }<br /> { \frac { 3 } { 4 } + \frac { 1 } { 2 } t } \\<br /> { – \frac { 1 } { 4 } – \frac { 1 } { 2 } t }<br /> \end {array} } \right ] { e ^ t } }<br /> = { \frac { 1 } { 4 } { e ^ t } \left [ { \begin {array} { * { 2 0 }{ c } }<br /> { 3 + 2 t } \\<br /> { – 1 – 2 t }<br /> \end {array} } \right ] . } $$

جواب نهایی دستگاه ناهمگن به صورت زیر است:‌

$$ \large { \mathbf { X } \left ( t \right ) = { \mathbf { X } _ 0 } \left ( t \right ) + { \mathbf { X } _ 1 } \left ( t \right ) }<br /> \\ \large = { { C _ 1 } { e ^ { 2 t } } \left [ { \begin {array} { * { 2 0 } { c } }<br /> 1 \\<br /> 0<br /> \end {array} } \right ] }<br /> + { { C _ 2 } { e ^ { 3 t } } \left [ { \begin {array} { * { 2 0 }{ c} }<br /> 1 \\<br /> 1<br /> \end {array} } \right ] }<br /> + { \frac { 1 } { 4 } { e ^ t } \left [ { \begin {array} { * { 2 0 } { c } }<br /> { 3 + 2 t } \\<br /> { – 1 – 2 t }<br /> \end {array} } \right] . } $$

مثال ۳

دستگاه معادلات زیر را با استفاده از روش تغییر پارامترها حل کنید:

$$\large {\frac{{dx}}{{dt}} = y + \frac{1}{{\cos t}},\;\;}\kern-0.3pt{\frac{{dy}}{{dt}} = – x.}$$

حل: ابتدا جواب عمومی دستگاه همگن را می‌نویسیم. مقادیر ویژه به صورت زیر محاسبه می‌شوند:

$$ \large {A = \left[ {\begin{array}{*{20}{r}}<br /> 0&1\\<br /> { – 1}&0<br /> \end{array}} \right],\;\;}\Rightarrow<br /> {{\det \left( {A – \lambda I} \right) }={ \left| {\begin{array}{*{20}{r}}<br /> {-\lambda} &1\\<br /> { – 1}&{ – \lambda }<br /> \end{array}} \right| = 0,\;\;}}\\ \large \Rightarrow<br /> {{\lambda ^2} + 1 = 0,\;\;}\Rightarrow<br /> {{\lambda ^2} = – 1,\;\;}\Rightarrow<br /> {{\lambda _{1,2}} = \pm i.} $$

بردار ویژه مختلط $${\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T}$$ را برای مقدار ویژه $${\lambda _1} = + i$$ به دست می‌آوریم:

$$ \large {\left( {A – {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{r}}<br /> { – i}&1\\<br /> { – 1}&{ – i}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;}\Rightarrow<br /> { – i{V_{11}} + {V_{21}} = 0.} $$

با قرار دادن $${V_{11}} = t$$، مقدار $${V_{21}} = i{V_{11}} = it$$ حاصل می‌شود. در نتیجه، داریم:

$$ \large {{\mathbf{V}_1} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \left[ {\begin{array}{*{20}{c}}<br /> t\\<br /> {it}<br /> \end{array}} \right] }<br /> = {t\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> i<br /> \end{array}} \right] }<br /> \sim {\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> i<br /> \end{array}} \right].} $$

مقدار ویژه $${\lambda _1}$$ و بردار ویژه $${\mathbf{V}_1}$$، متناظر با جوابی به فرم زیر هستند:

$$ \large {{\mathbf{Z}_1}\left( t \right) = {e^{{\lambda _1}t}}{\mathbf{V}_1} = {e^{it}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> i<br /> \end{array}} \right] }<br /> = {\left( {\cos t + i\sin t} \right)\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> i<br /> \end{array}} \right] }<br /> \\ \large = {\left[ {\begin{array}{*{20}{c}}<br /> {\cos t + i\sin t}\\<br /> {i\cos t – \sin t}<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> {\cos t}\\<br /> { – \sin t}<br /> \end{array}} \right] + i\left[ {\begin{array}{*{20}{c}}<br /> {\sin t}\\<br /> {\cos t}<br /> \end{array}} \right].} $$

بخش‌های حقیقی و موهومی عبارت اخیر، دستگاه اساسی جواب‌ها را تشکیل می‌دهند:

$$ \large {{\mathbf{X}_0}\left( t \right) }={ {C_1}\left[ {\begin{array}{*{20}{c}}<br /> {\cos t}\\<br /> { – \sin t}<br /> \end{array}} \right] }+{ {C_2}\left[ {\begin{array}{*{20}{c}}<br /> {\sin t}\\<br /> {\cos t}<br /> \end{array}} \right]} $$

که در آن، $$C_1$$ و $$C_2$$ توابعی از متغیر $$t$$ هستند:

$$\large \left\{ \begin{array}{l} {x\left( t \right) }={ {C_1}\left( t \right)\cos t + {C_2}\left( t \right)\sin t}\\ {y\left( t \right) }={ – {C_1}\left( t \right)\sin t + {C_2}\left( t \right)\cos t} \end{array} \right..$$

اکنون دستگاه ناهمگن را بررسی می‌کنیم. طبق روش تغییر ثوابت، فرض می‌کنیم $$C_1$$ و $$C_2$$ توابعی از متغیر $$t$$ باشند:‌

$$\large \left\{ \begin{array}{l} {x\left( t \right) }={ {C_1}\left( t \right)\cos t + {C_2}\left( t \right)\sin t}\\ {y\left( t \right) }={ – {C_1}\left( t \right)\sin t + {C_2}\left( t \right)\cos t} \end{array} \right..$$

با جایگذاری فرمول‌های اخیر در دستگاه ناهمگن اصلی، داریم:

$$\large {\left\{ \begin{array}{l} {{C’_1}\cos t – \cancel{{C_1}\sin t} }+{ {C’_2}\sin t + \cancel{{C_2}\cos t} }={ – \cancel{{C_1}\sin t} + \cancel{{C_2}\cos t} }+{ \frac{1}{{\cos t}} }\\ { – {C’_1}\sin t – \cancel{{C_1}\cos t} }+{ {C’_2}\cos t – \cancel{{C_2}\sin t} }={ – \cancel{{C_1}\cos t} – \cancel{{C_2}\sin t} } \end{array} \right.,\;\;} \\ \large \Rightarrow {\left\{ \begin{array}{l} {C’_1}\cos t + {C’_2}\sin t = \frac{1}{{\cos t}}\\ – {C’_1}\sin t + {C’_2}\cos t = 0 \end{array} \right.}$$

دستگاه معادلات اخیر را حل کرده و توابع $$C_1(t)$$ و $$C_2 (t)$$ را به دست می‌آوریم. این کار را می‌توان به سادگی با استفاده از قاعده کرامر انجام داد:

$$ \large {{\Delta = \left| {\begin{array}{*{20}{r}}<br /> {\cos t}&{\sin t}\\<br /> { – \sin t}&{\cos t}<br /> \end{array}} \right| }={ {\cos ^2}t + {\sin ^2}t = 1,\;\;}}\kern-0.3pt<br /> \\ \large {{{\Delta _1} = \left| {\begin{array}{*{20}{c}}<br /> {\frac{1}{{\cos t}}}&{\sin t}\\<br /> 0&{\cos t}<br /> \end{array}} \right| }={ \frac{1}{{\cos t}} \cdot \cos t – 0 = 1,\;\;}}\kern-0.3pt<br /> \\ \large {{{\Delta _2} = \left| {\begin{array}{*{20}{r}}<br /> {\cos t}&{\frac{1}{{\cos t}}}\\<br /> { – \sin t}&0<br /> \end{array}} \right| }={ 0 + \frac{1}{{\cos t}} \cdot \sin t }={ \tan t.}} $$

بنابراین، داریم:

$$\large {{C’_1} = \frac{{{\Delta _1}}}{\Delta } = \frac{1}{1} = 1,\;\;}\kern-0.3pt {{C’_2} = \frac{{{\Delta _2}}}{\Delta } = \frac{{\tan t}}{1} }={ \tan t.}$$

از معادله بالا انتگرال می‌گیریم:

$$\large { { C_1}\left( t \right) = \int {1dt} = t + {A_1},\;\;}\kern-0.3pt {{C_2}\left( t \right) = \int {\tan tdt} } \\ \large = {\int {\frac{{\sin t}}{{\cos t}}dt} } = { – \int {\frac{{d\left( {\cos t} \right)}}{{\cos t}}dt} } = { – \ln \left| {\cos t} \right| + {A_2}}$$

که در آن، $$A_1$$ و $$A_2$$ ثابت‌های انتگرال‌گیری هستند.

در نتیجه، عبارات زیر را برای $$x(t)$$ و $$y(t)$$ خواهیم داشت:

$$\large {{x\left( t \right) }={ {C_1}\left( t \right)\cos t }+{ {C_2}\left( t \right)\sin t }} \\ \large = {{\left( {t + {A_1}} \right)\cos t }}+{{ \left( { – \ln \left| {\cos t} \right| + {A_2}} \right)\sin t }} \\ \large = {{{A_1}\cos t + {A_2}\sin t }+{ t\cos t }-{ \sin t\ln \left| {\cos t} \right|,}}$$

و

$$\large {{y\left( t \right) }={ – {C_1}\left( t \right)\sin t }+{ {C_2}\left( t \right)\cos t }} \\ \large = {{ – \left( {t + {A_1}} \right)\sin t }+{ \left( { – \ln \left| {\cos t} \right| + {A_2}} \right)\cos t }} \\ \large = {{ – {A_1}\sin t + {A_2}\cos t }-{ t\sin t }-{ \cos t\ln \left| {\cos t} \right|.}}$$

دو جمله اول با ضرایب $$A_1$$ و $$A_2$$ در هر عبارت، جواب دستگاه همگن را توصیف می‌کنند. جملات باقیمانده به بخش ناهمگن مربوط هستند. جواب نهایی را می‌توان به صورت زیر نوشت:

$$ \large {\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> {x\left( t \right)}\\<br /> {y\left( t \right)}<br /> \end{array}} \right] }<br /> = {{A_1}\left[ {\begin{array}{*{20}{c}}<br /> {\cos t}\\<br /> { – \sin t}<br /> \end{array}} \right] }<br /> + {{A_2}\left[ {\begin{array}{*{20}{c}}<br /> {\sin t}\\<br /> {\cos t}<br /> \end{array}} \right] }<br /> + {\left[ {\begin{array}{*{20}{c}}<br /> {t\cos t – \sin t\ln \left| {\cos t} \right|}\\<br /> { – t\sin t – \cos t\ln \left| {\cos t} \right|}<br /> \end{array}} \right].} $$

مثال ۴

جواب دستگاه ناهمگن خطی زیر را با استفاده از روش تغییر ثوابت محاسبه کنید:

$$\large {\frac{{dx}}{{dt}} = 2x – y + {e^{2t}},\;\;}\kern-0.3pt {{\frac{{dy}}{{dt}} = 6x – 3y }+{ {e^t} + 1.}}$$

حل:‌ ابتدا جواب عمومی دستگاه همگن را محاسبه می‌کنیم. مقادیر ویژه ماتریس $$A$$ به صورت زیر به دست می‌آیند:

$$ \large {\det \left( {A – \lambda I} \right) = \left| {\begin{array}{*{20}{c}}<br /> 2&{ – 1}\\<br /> 6&{ – 3}<br /> \end{array}} \right| = 0,\;\;}\Rightarrow<br /> {\left( {2 – \lambda } \right)\left( { – 3 – \lambda } \right) + 6 = 0,\;\;} \\ \large \Rightarrow<br /> {\left( {\lambda – 2} \right)\left( {\lambda + 3} \right) + 6 = 0,\;\;}\Rightarrow<br /> {{\lambda ^2} – 2\lambda + 3\lambda – \cancel{6} + \cancel{6} = 0,\;\;} \\ \large \Rightarrow<br /> {{\lambda ^2} + \lambda = 0,\;\;} \Rightarrow<br /> {\lambda \left( {\lambda + 1} \right) = 0,\;\;}\Rightarrow<br /> {{\lambda _1} = 0,\;{\lambda _2} = – 1.} $$

بردار ویژه $${\mathbf{V}_1} = {\left( {{V_{11}},{V_{21}}} \right)^T}$$ متناظر با مقدار ویژه $${\lambda _1} = 0$$ برابر است با:

$$ \large {\left( {A – {\lambda _1}I} \right){\mathbf{V}_1} = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> 2&{ – 1}\\<br /> 6&{ – 3}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] = \mathbf{0},\;\;} \\ \large \Rightarrow<br /> {2{V_{11}} – {V_{21}} = 0,\;\;}\Rightarrow<br /> {{V_{11}} = t,}\;\;<br /> {{V_{21}} = 2{V_{11}} = 2t,\;\;} \\ \large \Rightarrow<br /> {{\mathbf{V}_1} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{11}}}\\<br /> {{V_{21}}}<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> t\\<br /> {2t}<br /> \end{array}} \right] }<br /> = {t\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 2<br /> \end{array}} \right] }<br /> \sim {\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 2<br /> \end{array}} \right].} $$

به طور مشابه، بردار ویژه $${\mathbf{V}_2} = {\left( {{V_{12}},{V_{22}}} \right)^T}$$ متناظر با مقدار ویژه $${\lambda _2} = -1$$ را محاسبه می‌کنیم:

$$ \large {\left( {A – {\lambda _2}I} \right){\mathbf{V}_2} = \mathbf{0},\;\;}\Rightarrow<br /> {\left[ {\begin{array}{*{20}{c}}<br /> 3&{ – 1}\\<br /> 6&{ – 2}<br /> \end{array}} \right]\left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] = \mathbf{0},\;\;} \\ \large \Rightarrow<br /> {3{V_{12}} – {V_{22}} = 0,\;\;}\Rightarrow<br /> {{V_{12}} = t,}\;\;<br /> {{V_{22}} = 3{V_{12}} = 3t,\;\;} \\ \large \Rightarrow<br /> {{\mathbf{V}_2} = \left[ {\begin{array}{*{20}{c}}<br /> {{V_{12}}}\\<br /> {{V_{22}}}<br /> \end{array}} \right] }<br /> = {\left[ {\begin{array}{*{20}{c}}<br /> t\\<br /> {3t}<br /> \end{array}} \right] }<br /> = {t\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 3<br /> \end{array}} \right] }<br /> \sim {\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 3<br /> \end{array}} \right].} $$

بنابراین، جواب عمومی دستگاه معادلات همگن برابر است با:

$$ \large {{\mathbf{X}_0}\left( t \right) }={ \left[ {\begin{array}{*{20}{c}}<br /> {{x_0}\left( t \right)}\\<br /> {{y_0}\left( t \right)}<br /> \end{array}} \right] }<br /> = {{C_1}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 2<br /> \end{array}} \right] + {C_2}{e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 3<br /> \end{array}} \right]} $$

که در آن، $$C_1$$ و $$C_2$$ اعداد ثابتی هستند.

اکنون دستگاه ناهمگن اصلی را در نظر گرفته و جواب آن را با استفاده از تغییر پارامترها به دست می‌آوریم. بدین منظور $$C_1$$ و $$C_2$$ را به ترتیب، با $$C_1(t)$$ و $$C_2(t)$$ جایگزین می‌کنیم؛ یعنی جواب را به فرم زیر می‌نویسیم:

$$ \large {\mathbf{X}\left( t \right) }={ {C_1}\left( t \right)\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 2<br /> \end{array}} \right] }+{ {C_2}\left( t \right){e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 3<br /> \end{array}} \right]} $$

یا

$$\large \left\{ \begin{array}{l} x\left( t \right) = {C_1}\left( t \right) + {C_2}\left( t \right){e^{ – t}}\\ y\left( t \right) = 2{C_1}\left( t \right) + 3{C_2}\left( t \right){e^{ – t}} \end{array} \right..$$

مشتق این توابع برابر است با:

$$\large \left\{ \begin{array}{l} {x’\left( t \right) }={ {C’_1} + {C’_2}{e^{ – t}} – {C_2}{e^{ – t}} }\\ {y’\left( t \right) }={ 2{C’_1} + 3{C’_2}{e^{ – t}} – 3{C_2}{e^{ – t}} } \end{array} \right..$$

در ادامه، عبارات بالا را در دستگاه ناهمگن قرار می‌دهیم:

$$ \large {\left\{ \begin{array}{l}<br /> {{C’_1} + {C’_2}{e^{ – t}} – \cancel{{C_2}{e^{ – t}}} }={ \cancel{2{C_1}} + \cancel{2{C_2}{e^{ – t}}} }-{ \cancel{2{C_1}} – \cancel{3{C_2}{e^{ – t}}} }+{ {e^{2t}} }\\<br /> {2{C’_1} + 3{C’_2}{e^{ – t}} – \cancel{3{C_2}{e^{ – t}}} }={ \cancel{6{C_1}} + \cancel{6{C_2}{e^{ – t}}} }-{ \cancel{6{C_1}} – \cancel{9{C_2}{e^{ – t}}} }+{ {e^t} + 1}<br /> \end{array} \right.,\;\;} \\ \large \Rightarrow<br /> {\left\{ {\begin{array}{*{20}{l}}<br /> {{C’_1} + {C’_2}{e^{ – t}} = {e^{2t}}}\\<br /> {2{C’_1} + 3{C’_2}{e^{ – t}} = {e^t} + 1}<br /> \end{array}} \right.} $$

اکنون دو معادله جبری برای $${C’_1}$$ و $${C’_2}$$ داریم. با حل این دستگاه معادلات، می‌توان توابع $$C_1(t)$$ و $$C_2(t)$$ را نیز به دست آورد.

$$ \large {\Delta = \left| {\begin{array}{*{20}{c}}<br /> 1&{{e^{ – t}}}\\<br /> 2&{3{e^{ – 2t}}}<br /> \end{array}} \right| }<br /> = {3{e^{ – t}} – 2{e^{ – t}} = {e^{ – t}},} $$

$$ \large {{\Delta _1} = \left| {\begin{array}{*{20}{c}}<br /> {{e^{2t}}}&{{e^{ – t}}}\\<br /> {{e^t} + 1}&{3{e^{ – 2t}}}<br /> \end{array}} \right| }<br /> = {3{e^{2t}}{e^{ – t}} – {e^{ – t}}\left( {{e^t} + 1} \right) }<br /> = {3{e^t} – {e^{ – t}} – 1,} $$

$$ \large {{\Delta _2} = \left| {\begin{array}{*{20}{c}}<br /> 1&{{e^{2t}}}\\<br /> 2&{{e^t} + 1}<br /> \end{array}} \right| }<br /> = {{e^t} – 2{e^{2t}} + 1,} $$

$$\large \Rightarrow{ {C’_1} = \frac{{{\Delta _1}}}{\Delta } }={ \frac{{3{e^t} – {e^{ – t}} – 1}}{{{e^{ – t}}}} } = {3{e^{2t}} + {e^t} – 1,}$$

$$\large \Rightarrow{ {C’_2} = \frac{{{\Delta _2}}}{\Delta } }={ \frac{{{e^t} – 2{e^{2t}} + 1}}{{{e^{ – t}}}} } = {{e^{2t}} – 2{e^{3t}} + {e^t}.}$$

با انتگرال‌گیری، عبارات مورد نظر محاسبه می‌شود:‌

$$\large {{C_1}\left( t \right) }={ \int {\left( {3{e^{2t}} + {e^t} – 1} \right)dt} } = {\frac{3}{2}{e^{2t}} + {e^t} – t + {A_1},}$$

$$\large {{C_2}\left( t \right) }={ \int {\left( {{e^{2t}} – 2{e^{3t}} + {e^t}} \right)dt} } = {\frac{1}{2}{e^{2t}} – \frac{2}{3}{e^{3t}} + {e^t} + {A_2}.}$$

در نتیجه، توابع $$x(t)$$ و $$y(t)$$ به فرم زیر خواهند بود:‌

$$\large {x\left( t \right) = {C_1}\left( t \right) + {C_2}\left( t \right){e^{ – t}} } \\ \large = {{\left( {\frac{3}{2}{e^{2t}} + {e^t} – t + {A_1}} \right) } + {\left( {\frac{1}{2}{e^{2t}} – \frac{2}{3}{e^{3t}} }\right.}+{\left.{ {e^t} + {A_2}} \right){e^{ – t}} }} \\ \large = {{A_1} + {A_2}{e^{ – t}} + \frac{5}{9}{e^{2t}} } + {\frac{3}{2}{e^t} – t + 1}$$

و

$$\large {y\left( t \right) = 2{C_1}\left( t \right) + 3{C_2}\left( t \right){e^{ – t}} } \\ \large = {{2\left( {\frac{3}{2}{e^{2t}} + {e^t} – t + {A_1}} \right) } + {3\left( {\frac{1}{2}{e^{2t}} – \frac{2}{3}{e^{3t}} }\right.}+{\left.{ {e^t} + {A_2}} \right){e^{ – t}} }} \\ \large = {2{A_1} + 3{A_2}{e^{ – t}} + {e^{2t}} } + {\frac{7}{2}{e^t} – 2t + 3.}$$

جواب نهایی را می‌توان به صورت زیر نوشت:‌

$$ \large {\mathbf{X}\left( t \right) = \left[ {\begin{array}{*{20}{c}}<br /> {x\left( t \right)}\\<br /> {y\left( t \right)}<br /> \end{array}} \right] }<br /> = {{A_1}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 2<br /> \end{array}} \right] }+{ {A_2}{e^{ – t}}\left[ {\begin{array}{*{20}{c}}<br /> 1\\<br /> 3<br /> \end{array}} \right] }<br /> + {\left[ {\begin{array}{*{20}{c}}<br /> {\frac{5}{9}{e^{2t}} + \frac{3}{2}{e^t} – t + 1}\\<br /> {{e^{2t}} + \frac{7}{2}{e^t} – 2t + 3}<br /> \end{array}} \right].} $$

توجه کنید که بخش ناهمگن این مسئله، از شبه‌چندجمله‌ای تشکیل شده است. بنابراین، جواب دستگاه معادلات را می‌توان با استفاده از روش ضرایب نامعین و اصل جمع آثار نیز به دست آورد.