توابع اکسل در حسابداری — آموزش توابع پرکاربرد به زبان ساده

در سالهای ۱۹۷۰ تا ۱۹۸۰، پدیدهای نو ظهور به نام کامپیوتر شخصی (PC) پردهبرداری شد. شاید بتوان علت اصلی فروش بیسابقه کامپیوترهای شخصی و همچنین تولد شرکتهای نرمافزاری جدید را بهرهبرداری از نرمافزارهای صفحه گسترده (Spreadsheet) دانست. شرکت Lotus، نرمافزار ۳-۲-۱ را معرفی کرد. همچنین نرمافزار VisiCalc یکی از نرمافزارها صفحه گسترده پیشرو بود. شرکت مایکروسافت، Multiplan و شرکت بُرلند، نرمافزار صفحه گسترده QuatroPro را به صورتی تجاری عرضه کردند. البته امروزه با تغییر صاحبان این محصولات، تقریبا به جز اکسل، کسی از صفحه گستردههای قدیمی خبری ندارد. اکسل نیز در سال ۱۹۸۵ همگام با معرفی گروه نرمافزارهای آفیس ظاهر گشت. در ابتدا بیشترین کاربرد چنین صفحه گستردههایی در امور حسابداری بود. به تدریج فرمولهای حسابداری نیز در قالب توابع ارائه شدند. توابع اکسل در حسابداری یکی از رازهای موفقیت این صفحه گسترده نسبت به رقیبها محسوب میشود. به همین جهت در این متن به معرفی توابع اکسل در حسابداری میپردازیم و با ذکر بعضی از مثالها، زاویای آنها را روشنتر میکنیم.
در مطلب «آموزش اکسل در حسابداری و مهارت هایی که باید یاد بگیرید»، بسیاری از نکات مرتبط با لزوم یادگیری اکسل برای انجام فعالیتهای مرتبط با رشته حسابداری را توضیح دادیم. در این مطلب از مجله فرادرس، به آموزش توابع تخصصی حسابداری در اکسل میپردازیم.
توابع اکسل در حسابداری
نرم افزار اکسل، مهمترین ابزار بانکداران سرمایهگذاری و تحلیل گران مالی است. آنها بیش از 70٪ از وقت خود را صرف تهیه مدلهای مالی، فرمول بندی فرضیات، ارزیابیها، محاسبات، نمودارها و غیره توسط به کارگیری توابع اکسل در حسابداری میکنند. میتوان فرض کرد که بانکداران و سرمایهگذاران استادان فرمول نویسی و به کارگیری ابزارهای اکسل هستند. توجه داشت باشید که بیش از 55 تابع مالی در اکسل وجود دارد ولی در اینجا لیستی از توابع اکسل در حسابداری مورد توجه قرار گرفته و به چهارده تابع مهم مالی اشاره خواهیم کرد.
برای دسترسی به توابع مالی در اکسل، کافی است از برگه Formula گزینه Financial را انتخاب کنید. لیست طولانی از توابع مالی در اکسل ظاهر خواهد شد. در ادامه به لیستی که در مورد توابع بازگشت سرمایه و وام کاربرد دارند، اشاره خواهیم کرد.
- تابع ارزش آتی (FV)
- تابع FVSCHEDULE
- تابع ارزش فعلی (PV)
- تابع ارزش خالص فعلی (NPV)
- تابع XNPV
- تابع PMT
- تابع PPMT
- تابع نرخ بازگشت داخلی (IRR)
- تابع نرخ بازگشت داخلی تغییر یافته (MIRR)
- تابع XIRR
- تابع NPER
- تابع RATE
- تابع EFFECT
- تابع NOMINAL
این توابع اکسل در حسابداری که به توابع مالی در اکسل نیز شهرت دارند را به کمک مثالهایی مورد بررسی قرار داده و پارامترهای آنها را مشخص و ویژگیهایشان را معرفی خواهیم کرد.
تابع FV یا ارزش آتی
یکی از پرکاربردترین توابع اکسل در حسابداری تابع FV یا ارزش آتی است. به کمک آن ارزش آینده یک سرمایه گذاری خاص را محاسبه میکنیم. البته باید توجه داشت که شرط استفاده از این تابع آن است که این سرمایهگذاری دارای نرخ بهره ثابت و پرداخت دورهای یکسان باشد. پارامترها و شکل نوشتاری این تابع به صورت زیر است.
= FV (Rate, Nper, [Pmt], PV, [Type])
که در آن پارامترها به صورت زیر هستند.
- ًRate (نرخ بهره): این پارامتر میزان بهره یا درصد سود در سرمایهگذاری را مشخص میکند. باید توجه داشت که زمان یا واحد زمانی برای نرخ بهره و بازده سرمایهگذاری یکسان باشد. برای مثال اگر نرخ بهره ماهانه است، نتیجه تابع FV، ارزش آتی را به تعداد واحدهای ماه سپری شده براساس Nper محاسبه میکند.
- Nper (دوره سرمایهگذاری): این پارامتر نیز تعداد دورههای سرمایهگذاری را مشخص میکند. باید واحد اندازهگیری دورهها (ماهانه یا سالانه) با واحد Rate یکسان باشد.
- [Pmt] (پرداخت): این پارامتر اختیاری است به همین جهت داخل علامت [ ] آن را نشان دادهایم. پرداختهای مربوط به هر دوره در این پارامتر مشخص میشود. باز هم یکسان بودن واحد زمان برای این پارامتر و پارامترهای دیگر از ضروریات محسوب میشود. در صورتی که مقداری برای این پارامتر در نظر گرفته نشود، اکسل آن را ۰ در نظر میگیرد.
- PV (ارزش فعالی): این پارامتر ارزش فعلی سرمایهگذاری است. مبلغی که در این پارامتر وارد میکنید، سرمایهگذاری اولیه را مشخص میکند.
- [Type] (نوع): این پارامتر نیز اختیاری است. اگر زمان پرداخت در ابتدای دوره تعیین شده باشد، مقدار ۱ و در غیر اینصورت، مقدار ۰ برای این پارامتر در نظر گرفته میشود. پیشفرض برای این پارامتر، مقدار صفر است.
به منظور بهرهگیری از توابع اکسل در حسابداری بخصوص تابع FV به ذکر یک مثال میپردازیم.
مثال: فردی در سال ۱۳۹۶ مبلغ یکصد میلیون تومان در یک صندوق سرمایهگذاری، مشارکت کرده است. پرداخت سالانه و با نرخ سود ۱۰٪ صورت میگیرد. ارزش آتی این سرمایهگذاری در سال 1399 چقدر است؟
راه حل: در اکسل، فرمول زیر را به کمک تابع FV مینویسیم.
= FV (10%, 3, 1, – 100)
توجه دارید که به علت فاصله سه سال بین سالهای ۱۳۹۶ تا ۱۳۹۹، پارامتر دوم را برابر با ۳ در نظر گرفتهایم تا نشانگر محاسبه در پایان سه دوره (سه سال) باشد. نتیجه یا حاصل این تابع، مقدار ۱۲۹٫۷۹ بوده که نشانگر یکصدوبیست و نه میلیون تومان است. به تصویر زیر نیز توجه کنید که در آن همین مسئله به قالب پارامتری دیده میشود.
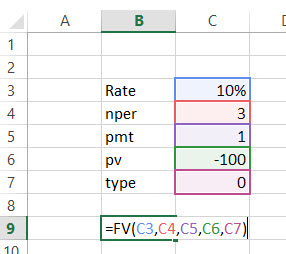
تابع FVSCHEDULE
این تابع مالی زمانی به کار میرود که ارزش آتی با نرخ سود متغیر محاسبه میشود ولی دورههای بازپرداخت یکسان است. شکل نوشتاری این تابع به صورت زیر است. در ادامه پارامترهای این تابع را هم معرفی خواهیم کرد.
= FVSCHEDULE (Principal, Schedule)
- Principal (اصل سرمایه): اصل ارزش فعلی یک سرمایه گذاری خاص را مشخص میکند.
- Schedule (زمانبندی): مجموعهای از نرخهای بهره که در هر دوره بازپرداخت مورد استفاده قرار میگیرد.
مثال: فردی در پایان سال ۱۳۹۶ به مبلغ یکصد میلیون تومان سرمایه گذاری کرده است. انتظار میرود که نرخ بهره هر ساله تغییر کند. در سالهای 1397 ، 1398 و 1399، نرخ بهره به ترتیب 4، 6 و 5 درصد است. FVSCHEDULE یا ارزش آتی سرماهیگذاری برنامهریزی شده در سال 1399 چگونه خواهد بود؟
راه حل: در یک کاربرگ اکسل، موارد زیر را انجام خواهیم داد. ابتدا مبلغ سرمایهگذاری را در سلولی وارد کرده و دورههای بازپرداخت را در یک ستون ثبت میکنیم. واضح است که این دورهها ثابت بوده ولی مبلغ یا نرخ سود متغیر است. به تصویر زیر توجه کنید.
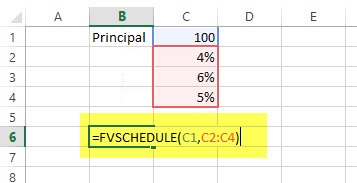
تابع را به صورت زیر در سلولی ثبت میکنیم. سلول C1 مقدار اصل سرمایه و C2 تا C4، ناحیه مربوط به درصدها یا نرخهای سود هستند.
= FVSCHEDULE (C1, C2: C4)
نتیجه این محاسبه مقداری برابر با ۱۱۵٫۷۵۲ است که نشانگر یکصد و پانزده میلیون تومان است. یعنی بعد از گذشت سه سال، مبلغ سرمایهگذاری شده مورد انتظار تقریبا ۱۵٪ افزایش داشته است.
تابع PV
همانطور که تابع FV ارزش آتی یک سرمایهگذاری را نشان میدهد، تابع PV نیز ارزش فعلی (Present Value) یک سرمایهگذاری را مشخص میکند. پارامترهای این تابع نیز درست به مانند تابع FV است. شکل دستوری این تابع به صورت زیر است. مشخص است که جای FV با PV در این تابع تغییر یافته ولی بقیه پارامترها مشابه هستند.
= PV (Rate, Nper, [Pmt], FV, [Type])
پارامترهای این تابع را در ادامه بازگو میکنیم.
- ًRate (نرخ بهره): این پارامتر میزان بهره یا درصد سود در سرمایهگذاری را مشخص میکند.
- Nper (دوره سرمایهگذاری): این پارامتر نیز تعداد دورههای سرمایهگذاری را مشخص میکند.
- [Pmt] (پرداخت): میزان نرخ پرداخت در هر دوره در این پارامتر مشخص میشود. مقدار پیشفرض برای این پارامتر، صفر است.
- FV (ارزش آتی): این پارامتر ارزش آتی یا آینده سرمایهگذاری را در پایان دوره سرمایهگذاری نشان میدهد.
- [Type] (نوع): این پارامتر اختیاری بوده و مقدار ۱ نشانگر پرداخت در ابتدای هر دوره و ۰ نیز بازپرداخت در پایان هر دوره را نشان میدهد.
نکته: وضعیتی که برای هماهنگی واحد زمانی برای پارامترها برای تابع FV بیان شد نیز برای تابع PV صادق است.
مثال: ارزش فعلی یک سرمایه گذاری در سال ۱۳۹۶ با پرداخت سالانه و نرخ بهره ۱۰٪ در هر سال چقدر است اگر در سال ۱۳۹۹، یکصد میلیون حاصل شده باشد.
راه حل: در اکسل، تابع FV را از گروه توابع مالی اکسل به صورت زیر به کار میبریم.
= PV (10%, 3, 1, – 100)
نتیجه برابر با 72٫64 خواهد بود که معادل ۷۲ میلیون تومان است ولی در پایان ۳ سال، ارزش آتی این سرمایهگذاری ۱۰۰ میلیون تومان است.
در تصویر زیر، همین مسئله را به صورت پارامتری و براساس مقادیر سلولهای مختلف حل کردهایم. ارتباطی ریاضیاتی بین این توابع اکسل در حسابداری یعنی PV ،FV و PMT به همراه RATE و NPER برقرار است.
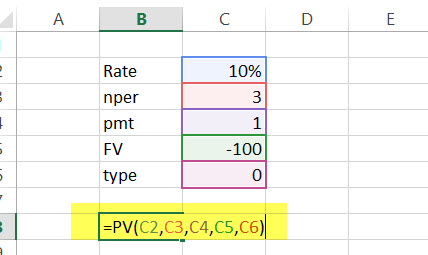
نکته: البته توابع اکسل در حسابداری بسیار شبیه هستند و گاهی پارامترهای یکسانی دارند. ولی نحوه محاسبه و فرمولبندی آنها برای رسیدن به هدف محاسباتی تفاوت دارد.
تابع NPV یا ارزش خالص فعلی
ارزش خالص فعلی، مجموع جریانهای نقدی مثبت و منفی در طول سالهای مختلف را مبنا در نظر گرفته و محاسبات را انجام میدهد. شکل دستوری این تابع به صورت زیر است.
= NPV (Rate, Value 1, [Value 2], [Value 3]…)
- Rate: نرخ بهره را مشخص میکند.
- Value1: مقدار جریان نقدی اول
- Value2, Value3: این پارامترها، اختیاری هستند ولی در صورتی که جریان نقدی بیش از یک بار صورت میگیرد باید مقدارهای آن را در هر دوره توسط این پارامترها مشخص کنید.
نکته: در اینجا، مقادیر منفی به عنوان پرداخت و مثبت به صورت دریافت در نظر گرفته میشوند.
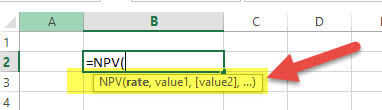
مثال: جدول زیر را در نظر بگیرید. میزان بازپرداخت در هر سال نوشته شده است. همچنین نرخ بهره و مبلغ سرمایهگذاری نیز در این جدول دیده میشود. ارزش خالص فعلی (NPV) را به کمک توابع اکسل در حسابداری محاسبه کنید.
جدول ۱: مقادیر پارامترهای مثال تابع NPV
| پارامتر | مشخصه | مقدار |
| نرخ بهره | Rate of Discount | |
| مبلغ اولیه سرمایهگذاری | Initial Investment | |
| مبلغ بازگشت در سال اول | Return from first year | |
| مبلغ بازگشت در سال دوم | Return from second year | |
| مبلغ بازگشت در سال سوم | Return from third year | |
| مبلغ بازگشت در سال چهارم | Return from 4th year |
راه حل: کاربرگ نمایش داده شده در تصویر زیر مقادیر بالا را در سلولهای اکسل نشان میدهد.
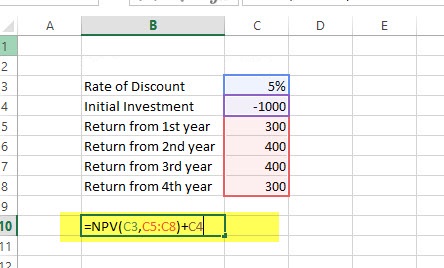
حاصل محاسبات صورت گرفته در این تابع مقدار ۲۴۰٫۸۷ است. بنابراین ارزش خالص فعلی این سرمایهگذاری در طی این چهار سال مشخص میشود. البته توجه دارید که مقدار اولیه که در سلول C4 قرار دارد نیز به ارزش خالص فعلی اضافه شده تا کل سرمایه را در پایان دورهها نشان دهد.
تابع XNPV
تابع XNPV به عنوان یکی از توابع اکسل در حسابداری برای محاسبه ارزش خالص فعلی به کار گرفته شده و البته مشابه تابع NPV است. باید توجه داشته باشید که در اینجا پرداخت و دریافتها دورهای نیستند. بلکه برای هر پرداخت و دریافت تاریخ مشخصی ذکر شده است که طول یا فاصله تاریخها در همهجا یکسان نیست. شکل دستوری این تابع به صورت زیر است.
= XNPV (Rate, Values, Dates)
همانطور که مشخص است، پارامترها «نرخ بهره» (Rate)، «مقدارهای دریافت وپرداخت» (Values) و همچنین «تاریخهای تراکنشهای مالی» (Dates) است. به مثالی که در ادامه برای شفاف کردن بیشتر این تابع ذکر شده، توجه کنید. به یاد داشته باشید که Values و Dates بردارهایی هستند که شامل مقادیر تراکنشها و تاریخهای مربوط به هر تراکنش هستند. در بعضی از توابع اکسل در حسابداری نیاز به برداری از مقادیر داریم که در اینجا به نمونهای از آن اشاره خواهیم کرد.
مثال: این بار هم جدولی به صورت زیر را در نظر بگیرید که شامل دریافت یا پرداختهای مستمر به همراه تاریخهای این تراکنشها است. برای راحتی کار، مقادیر را به تاریخ میلادی نوشته و واحد پول را هم هزار ریال در نظر گرفتهایم. یعنی مقدار ۱۰۰۰ نشانگر یک میلیون ریال است.
جدول ۲: مقادیر پارامترهای مثال تابع XNPV
| پارامتر | مشخصه | مقدار |
| نرخ بهره | Rate of Discount | |
| مقدار اولیه اول دسامبر ۲۰۱۱ | Initial Investment | |
| اولین تراکنش در تاریخ اول ژانویه ۲۰۱۲ | Return from first year | |
| دومین تراکنش در تاریخ اول فوریه ۲۰۱۳ | Return from second year | |
| سومین تراکنش در تاریخ اول مارچ ۲۰۱۴ | Return from third year | |
| چهارمین تراکنش در تاریخ اول آوریل ۲۰۱۵ | Return from 4th year |
راه حل: کاربرگ زیر به منظور نمایش این اطلاعات و محاسبه XPNV به کار رفته است.
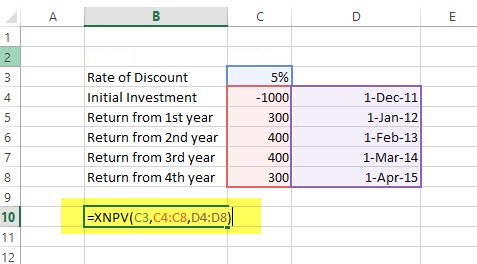
همانطور که در تصویر بالا مشاهده میکنید، ناحیه مربوط به تراکنشها وتاریخها باید یک اندازه باشند. در غیراینصورت با پیغام خطا مواجه خواهید شد. نتیجه اجرای تابع یا فرمول زیر برابر با 289٫9 خواهد بود.
=XNPV (5%, B2:B6, C2:C6)
تابع PMT
تابع PMT یکی از محبوبترین توابع اکسل در حسابداری است که به منظور تعیین اقساط یک وام با پرداخت دورهای ثابت با نرخ مشخص به کار میرود. شکل دستوری این تابع به صورت زیر است.
= PMT (Rate, Nper, PV, [FV], [Type])
واضح است که پارامترهای این تابع نیز کاملاً با تابع PV یا FV مشابه است. در حقیقت هر یک از این پارامترها میتواند برای تعیین پارامترهای دیگر به کار رود. واضح است که FV و Type دو پارامتر اختیاری محسوب میشوند. هنگام استفاده از این تابع باید واحد زمانی یکسان برای پارامترها را هم در نظر داشته باشید. در ادامه به یک مثال برای آشنایی بیشتر با این تابع میپردازیم.
مثال: یک وام به ارزش یک هزار میلیون ریال با نرخ بهره ۱۰٪ و تعداد اقساط ۳ ساله مورد نظر است. مبلغ اقساط برای هر سال چقدر خواهد بود. برای سادگی یک هزار میلیون ریال را به صورت ۱۰۰۰ درج میکنیم.
راه حل: طبق تصویر زیر، پارامترها را وارد کرده و تابع را براساس آنها مینویسیم.
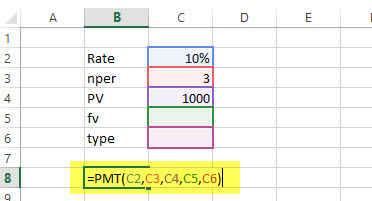
البته نتیجه فرمول زیر نیز به همین مثال ارتباط دارد. واضح است که باید در سال ۴۰۱ هزار میلیون ریال قسط پرداخت شود. البته این مقدار به صورت منفی ظاهر میشود زیرا به صورت پرداخت در نظر گرفته شده است.
= PMT (0.1 , 3 , 1000 )
نکته: توجه داشته باشید که اگر لازم بود اقساط ماهانه را در نظر بگیرید، باید Nper برابر با ۳۶ و نرخ بهره (Rate) نیز به صورت نوشته میشود.
نتیجه محاسبه PMT درون سلول با قالب Currency نمایش داده شده تا نشانگر عدد با واحد ارزی باشد.
تابع PPMT
این تابع نسخه دیگری از تابع PMT محسوب میشود. تنها تفاوت در این مورد است که تابع PPMT بخش اصل از بازپرداخت وام را مشخص میکند. حرف P اضافه شده در اسم تابع از عبارت Principle یا اصل گرفته شده است. بنابراین PPMT نشانگر Principal Payment یا اصل بازپرداخت است. تابع PPMT نیز یکی از کاربردیترین توابع اکسل در حسابداری است. شکل دستوری تابع به صورت زیر نوشته میشود.
= PPMT (Rate, Per, Nper, PV, [FV], [Type])
در اینجا هم پارامترها شبیه تابع PMT است با این تفاوت که پارامتر Per مربوط به دورهای است که باید اصل بازپرداخت در آن محاسبه شود. مثال زیر به بررسی این تابع برای یک وام و بازپرداخت اصل آن در سال اول پرداخته است.
مثال: فرض کنید وامی به مبلغ ۱۰۰۰ (میلیون ریال) با اقساط سه ساله و نرخ بهره سالانه ۱۰٪ دریافت شده است. مبلغ اصل پرداختی از وام در سال اول چقدر است؟ این مقدار را با اصل پرداختی از وام در سال دوم مقایسه کنید.
راه حل: توجه داریم که همه پارامترها بر حسب واحد زمان سال هستند. بنابراین نتیجه تابع PPMT نیز اصل وام در هر سال را مشخص میکند.
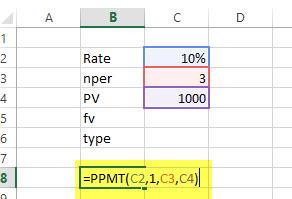
نتیجه در این حالت برابر است با ۳۰۲٫۱۱- است. توجه داشته باشید که وام دریافتی با مقدار مثبت و اقساط با مقدار منفی مشخص شده است.
فرمول زیر نیز به همین منظور قابل استفاده است.
=PPMT (10%, 1, 3, 1000)
برای سال دوم نیز همین محاسبات را به کار میبریم. به تصویر ۹ توجه کنید.
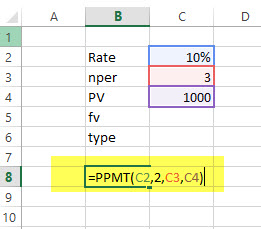
نتیجه محاسبه مربوط به تصویر 9 و فرمول زیر، مقدار ۳۳۲٫۳۳- است که از سال اول بیشتر است. این نشان میدهد که مبلغ پرداخت از قسط وام در سال اول بیشتر مربوط به سود وام و کمتر مربوط به اصل وام است. در سال دوم این حالت تغییر کرده و بیشتر مبلغ پرداخت قسط، مربوط به اصل و کمتر مربوط به سود وام است. از آنجایی مقدار تابع PPMT به صورت پولی است، اکسل به طور خودکار نتیجه را در سلولی با قالب Currency نشان میدهد.
نکته: توابع PMT، PPMT و IPMT به منظور محاسبه اقساط، اصل قسط و سود قسط به کار میروند.
تابع IRR
عبارت IRR مخفف Internal Rate of Return یا نرخ بازگشت داخلی است. این تابع در اکسل برای نشان دادن سوددهی یک پروژه در طرحهای توجیهی به کار میرود. اغلب شرکتها از این تابع برای جذب سرمایهگذار و تشویق آنها برای سرمایهگذاری نسبت به شرکتهای رقیب استفاده میکنند. شکل دستوری این تابع به صورت زیر است.
= IRR (Values, [Guess])
همانطور که واضح است، پارامتر Values برداری است که مبلغهای بازگشت سرمایه را نشان میدهد. این پارامتر یک بردار در اکسل را مشخص میکند. ممکن است مقادیر این بردار مثبت (دریافت) یا منفی (پرداخت) باشند. همچنین برای پیدا کردن سریعتر IRR میتوانید از یک مقدار حدسی به نام Guess استفاده کنید که البته اختیاری است. مثال زیر برای روشنتر شدن نحوه استفاده از این تابع معرفی شده است.
مثال: اطلاعات مربوط به جدول ۲ را در نظر بگیرید. نرخ بازگشت داخلی برای این دادهها چقدر است؟
راه حل: از تابع IRR به شکل زیر برای حل مسئله کمک میگیریم.
= IRR (C3:C7, 0.1)
همانطور که در تصویر ۱۱ مشاهده میکنید، سلولهای C3 تا C7 مربوط به مقادیر دریافتی به همراه مبلغ اولیه پرداختی است که کل جریان نقدی را شامل میشود. واضح است که ۰٫۱ نیز حدس اولیه برای مقدار IRR در نظر گرفته شده. نتیجه این محاسبه برابر با ۱۵٪ است.
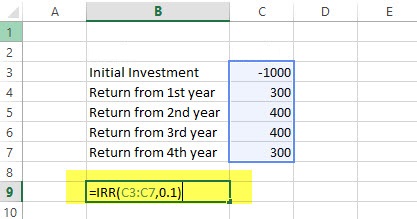
نکته: توجه داشته باشید که در ناحیه مربوط به پارامتر اول، مقدار پرداختی (Initial Investment) با علامت منفی و مقادیر دریافتی با علامت مثبت وارد شدهاند. به این ترتیب تمامی تراکنشهای مالی (دریافت و پرداخت) باید در این ناحیه مشخص شده باشند.
تابع MIRR
«نرخ بازده داخلی اصلاح شده» (Modified Internal Rate of Return) یک قدم جلوتر از نرخ بازده داخلی است. MIRR به معنای سودآوری سرمایهگذاری است و در تجارت استفاده میشود. تابع MIRR با فرض صفر بودن NPV محاسبه میشود. در اینجا پارامترهای مربوط به محاسبه تابع MIRR را معرفی میکنیم.
= MIRR (Values, Finance rate, Reinvestment rate)
- Values: جریانهای نقدی مثبت یا منفی (مجموعهای از مقادیر)
- Finance rate: نرخ بهره پرداخت شده برای پول مورد استفاده در جریانهای نقدی
- Reinvestment rate: نرخ بهره پرداخت شده برای سرمایهگذاری مجدد جریانهای نقدی
با ذکر یک مثال به بررسی این تابع و نحوه استفاده از پارامترها اشاره خواهیم کرد.
مثال: در اینجا یک سری داده مطابق با جدول ۲ را در نظر بگیرید و مقدار MIRR را پیدا کنید. توجه داشته باشید که نرخ بهره پرداخت (Finance rate) برابر با ۱۲٪ و نرخ بهره پرداخت شده برای سرمایهگذاری مجدد جریان نقدی نیز ۱۰٪ است.
راه حل: از تابع زیر کمک گرفته و محاسبات مربوط به MIRR را انجام میدهیم.
= MIRR (C2:C6, 12%, 10%)
کاربرگ اطلاعاتی برای حل این مثال نیز در تصویر ۱۲ دیده میشود. توجه دارید که در کاربرگ، نرخهای بهره در سلولهای C9 و C10 قرار گرفتهاند. نتیجه حاصل از محاسبه این تابع ۱۳٪ خواهد بود. همانطور که میبینید، MIRR نرخ بازگشت داخلی را یک درصد بیشتر از IRR محاسبه کرده است. زیرا نرخ بازسرمایهگذاری نیز در آن لحاظ شده است.

نکته: همانطور که در تصویر ۱۱ مشاهده میکنید، مقادیر پرداختی با علامت منفی مبالغ دریافتی با علامت مثبت دیده میشوند. همچنین توجه داشته باشید که فاصله بین تاریخهای پرداخت یا دریافت در هر دو تابع IRR و MIRR ثابت و برابر با یک سال است.
تابع XIRR
اگر تراکنشهای مالی برای محاسبه نرخ بازگشت داخلی، در تاریخها یا بازههای متفاوتی صورت گیرد، باید از تابع XIRR استفاده کنیم. مبنای محاسبات شبیه تابع IRR یا MIRR است ولی یک بردار برای مشخص کردن زمان یا تاریخ پرداختها نیز به عنوان پارامتر در تابع XIRR وجود دارد. شکل دستوری این تابع به صورت زیر است.
= XIRR (Values, Dates, [Guess])
واضح است که پارامتر Values جریان نقدی (مثبت یا منفی را مشخص کرده و Dates نیز تاریخ مربوط به هر یک از این تراکنشهای مالی را تعیین میکند. پارامتر Guess نیز اختیاری بوده و نرخ حدسی برای بازگشت سرمایه را برای سرعت بخشیدن به محاسبات نمایش میدهد. البته اگر این مقدار را وارد نکنید، اکسل طبق روشهای عددی، برای شروع الگوریتم محاسباتی، مقداری تصادفی برای آن در نظر خواهد گرفت.
باز هم در اینجا از جدولی برای نمایش جریانهای نقدی استفاده کرده و به ذکر مثالی به منظور روشنتر شدن نحوه به کار بردن پارامترها خواهیم پرداخت.
مثال: جدول زیر را در نظر بگیرید. جریان نقدی و تاریخ هر یک از آنها را در این جدول مشاهده میکنید. باز هم برای راحتی کار از تاریخهای میلادی کمک گرفتهایم. هر چند در نسخههای جدید اکسل ۲۰۱۹ امکان استفاده از تاریخهای شمسی نیز وجود دارد. واضح است که در ستون تاریخ، بازهها همگی یکساله و برابر نیستند. گاهی این فاصله ۱ ماه و گاهی ۱۳ ماه و گاهی ۳۹۷ روز است.
جدول ۳: مقادیر پارامترهای مثال تابع XNPV
| تاریخ | مشخصه | مقدار |
| اول دسامبر ۲۰۱۱ | سرمایهگذاری اولیه - Initial Investment | |
| اول ژانویه ۲۰۱۲ | Return from first year | |
| اول فوریه ۲۰۱۳ | Return from second year | |
| اول مارچ ۲۰۱۴ | Return from third year | |
| اول آپریل ۲۰۱۵ | Return from 4th year |
راه حل: به کاربرگی که در تصویر ۱۳ قابل مشاهده است، توجه کنید. اطلاعات مربوط به جدول ۳ در آن قرار گرفته است.
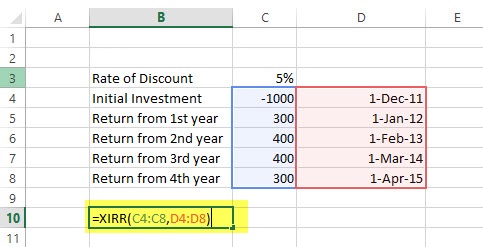
همانطور که میبینید در ستون C مقادیر جریان مالی و در ستون D نیز تاریخها مشخص شدهاند. توجه داشته باشید که تعداد سطرهای اطلاعاتی برای هر دو ستون باید یکسان باشند. پاسخ برای این مثال در نرخ بازگشت داخلی برابر با ۲۴٪ خواهد بود. همین محاسبات را به کمک فرمول زیر نیز میتوان انجام داد.
= XIRR (C4:C8, D4:D8, 0.1)
نکته: از آنجایی که معمولا مقدار تابع XIRR به صورت اعشاری و یا کسر کوچکتر از یک ظاهر میشود، اکسل به طور خودکار قالب سلول را به شکل Percentage درآورده و نتیجه را به صورت درصدی نمایش میدهد.
تابع NPER
یکی از توابع اکسل در حسابداری تابع NPER است که از محاسبات مربوط به PMT بهره میبرد. به این معنی که به کمک تابع NPER میتوان تعداد اقساط یک وام را با توجه به پارامترهای دیگر تابع PMT محاسبه کرد. شکل دستوری این تابع به صورت زیر است.
= NPER (Rate, PMT, PV, [FV], [Type])
مشخص است که پارامترهای این تابع درست به مانند پارامترهای تابع PMT است در نتیجه از تکرار آنها صرف نظر میکنیم. ولی باز هم تاکید میکنیم که نتیجه تابع NPER متناسب با واحد زمانی برای پارامترهای Rate و PMT است. یعنی اگر بازپرداخت وام ماهانه است، باید نرخ بهره را ماهانه وارد کرده تا نتیجه NPER تعداد اقساط را برحسب ماه محاسبه کند.
مثال: سالانه 200 هزارتومان برای یک وام یک میلیونی پرداخت میشود. نرخ بهره 10 درصد است و پرداخت باید سالانه انجام شود. NPER یا تعداد اقساط را پیدا کنید.
راه حل: در کاربرگی که در تصویر ۱۳ مشاهده میکنید، مقادیر مربوط به پارامترهای تابع NPER برای این مثال نوشته شده است. هر سلول نشانگر یکی از پارامترهای اصلی این تابع است.
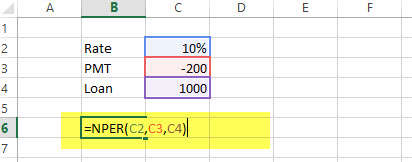
نتیجه اجرای این فرمول برابر با ۷٫۲۷ است. از آنجایی که همه مقادیر برحسب سال منظور شدهاند، این نتیجه هم براساس سال بدست میآید. پس ۷ سال و ۰٫۲۷ سال (۳ ماه و یک هفته) تعداد اقساط خواهد بود. باز هم توجه داشته باشید که مبلغ وام مثبت و مبلغ اقساط منفی وارد شدهاند تا نشانگر دریافت و پرداخت باشند.
میتوانستیم این محاسبات را به کمک فرمول زیر نیز انجام دهیم.
= NPER (10%, -200, 1000)
تابع RATE
از طریق تابع RATE در اکسل، میتوانیم نرخ بهره مورد نیاز برای پرداخت کامل وام را برای مدت زمان مشخص محاسبه کنیم. شکل دستوری این تابع و پارامترهای آن بسیار به تابع PMT یا NPER شبیه است. بنابراین از ذکر پارامترهای آنها پرهیز کرده و فقط به یک مثال در زمینه کاربرد تابع RATE به عنوان یکی از توابع اکسل در حسابداری خواهیم پرداخت.
= RATE (NPER, PMT, PV, [FV], [Type], [Guess])
مثال: 200 هزار تومان سال برای وام یک وام یک میلیون تومانی به مدت ۶ سال پیشنهاد شده است. نرخ سود سالانه این وام را مشخص کنید.
راه حل: کاربرگ زیر را برای نمایش پارامترهای تابع RATE در نظر میگیریم. واضح است که باید پارامتر NPER و PMT دارای واحد زمانی یکسانی باشند. نتیجه محاسبه تابع RATE در این حالت برابر است با ۵٪ است. بنابراین نرخ سود سالانه برای این وام ۵٪ خواهد بود.

البته فرمول زیر نیز برای حل این مسئله به کار میآید.
= RATE (6, -200, 1000, 0.1)
نکته: از آنجایی که مقدار تابع RATE باید به صورت درصدی نمایش داده شود، اکسل به طور خودکار، قالب سلول مربوط به تابع را به شکل درصدی در میآورد.
تابع EFFECT
از طریق تابع EFFECT میتوان «نرخ بهره سالانه موثر» (effective annual interest rate) را بدست آورد. وقتی «نرخ سود اسمی» (Nominal Interest Rate) و «تعداد ترکیب در سال» (Number of Compounding per Year) داشته باشیم، محاسبه نرخ موثر امکانپذیر میشود. شکل دستوری این تابع به صورت زیر است. پارامترهای این تابع در ادامه معرفی میشوند.
= EFFECT (Nominal_Rate, NPERY)
- Nominal_Rate: نرخ سود اسمی
- NPERY: تعداد ترکیب در سال
به منظور شناسایی نحوه کار با تابع EFFECT به عنوان یکی از توابع اکسل در حسابداری به مثال زیر توجه کنید.
مثال: پرداختهایی با نرخ سود اسمی ۱۲٪ صورت گرفته است. از طرفی تعداد ترکیب در سال نیز برابر با ۱۲ است. مقدار بهره سالانه موثر برای این پرداختها چقدر است؟
راه حل: کافی است فرمولی به صورت زیر در یک سلول کاربرگ اکسل وارد کنیم. نتیجه برابر با ۱۲٫۶۸٪ خواهد بود.
= EFFECT (12%, 12)
البته نحوه محاسبات به صورت پارامتری در تصویر 15 نیز دیده میشود.

نکته: هر چند این نرخ به صورت درصدی است ولی اکسل نمایش آن را به طور خودکار تعیین نمیکند. ولی بهتر است در ارائه گزارشات، قالب سلول محاسباتی را به شکل درصدی درآورید. این کار را در بیشتر توابع اکسل در حسابداری نیز باید به کار برد.
تابع NOMINAL
همانطور که در تابع EFFECT گفته شد، نرخ سود اسمی یکی از پارامترهای این تابع بود. اگر لازم است براساس سود موثر، نرخ سود اسمی را پیدا کنیم، از تابع NOMINAL که یکی دیگر از توابع اکسل در حسابداری است، کمک خواهیم گرفت. شکل دستوری این تابع به صورت زیر است.
= NOMINAL (Effect_Rate, NPERY)
مشخص است که پارامترهای این تابع با پارامترهای تابع EFFECT شبیه هستند. پس فقط به ذکر یک مثال اکتفا میکنیم.
مثال: طبق مثال قبل اگر تعداد ترکیب در سال 12 و نرخ سود موثر سالانه ۱۲٪ باشد، نرخ سود اسمی چقدر است؟
راه حل: با استفاده از تابع زیر مقدار مورد نظر را محاسبه میکنیم.
= NOMINAL (12%, 12)
نتیجه محاسبه برابر است با 11٫۳۹٪ که همان نرخ بهره یا سود اسمی است. در کاربرگی که در تصویر ۱۶ دیده میشود، همین محاسبه را به شکل یک فرمول وابسته نوشتهایم.

البته توابع اکسل در حسابداری متنوع هستند و حتی برای محاسبه استهلاک داراییها با شیوههای مختلف نیز توابعی میتوان پیدا کرد. به منظور آشنایی بیشتر با این توابع و نحوه کار با آنها به مطلب محاسبه استهلاک در اکسل — به زبان ساده مراجعه نمایید. در این مطلب تابع SLN برای محاسبه استهلاک خطی، تابع DB و DDB همینطور تابع VDB محاسبه استهلاک به روش نزولی (مضاعف) معرفی شدهاند. همچنین تابع SYD که براساس مجموع سنوات، استهلاک را محاسبه میکند، مورد توجه قرار گرفته است.
خلاصه و جمعبندی
توابع و محاسبات صفحه گستردهها بخصوص اکسل برای امور مالی ایجاد شدهاند. شاید توابع اکسل در حسابداری وجود داشته باشد که برای همه حسابدارها مورد نیاز نباشد. ولی تقریبا تمامی نیازهای افرادی که به نحوی در فعالیتهای تهیه گزارشهای مالی دخالت دارند در اکسل برآورده شده. توابع مربوط به وام، استهلاک و محاسبه سود یا نرخ رشد ایجاد شده و با تعیین چند پارامتر، توابع اکسل در حسابداری میتوانند پاسخها مناسب و البته دقیق به شما بدهند. در این نوشتار با دسته توابع مالی برای سرمایهگذاری و محاسبه سود، آشنا شدیم.












با درود و احترام
لطفا در صورت امکان فرمول ایجاد یک سطر بصورت اتوماتیک در یک جدول اکسلی به شرط تکمیل اطلاعات سطر قبلی را توضیح دهید .
با تشکر فراوان سروش همایون
سلام و درود بر شما همراه مجله فرادرس،
همانطور که اشاره کردید، سطرهای اکسل برای ورود داده ها محدودیتی ندارند بنابراین اگر پس از پر کردن یک سطر، سطر بعدی از کاربرگ را فعال کنید میتوانید مقادیر جدید را وارد کنید. ولی یک راه ساده برای حفظ ساختار و ایجاد یک جدول اطلاعاتی در کاربرگ اکسل، به کارگیری جدول (Table) است. در نوشتاری از مجله فرادرس به ساختار جدول و نحوه ایجاد و خصوصیات آن اشاره شده است. بهتر است با مطالعه مطلب ایجاد و رسم جدول در اکسل — به زبان ساده با این ابزار مفید اکسل بیشتر آشنا شوید. در این متن به نحوه ثبت سطر جدید در ساختار جدول نیز اشاره شده است.
موفق و تندرست باشید.