تحقیق در عملیات ۱ — آموزش رایگان و به زبان ساده + معرفی منابع

تحقیق در عملیات 1 یکی از دروس اصلی رشتههای مهندسی صنایع و مدیریت است. این درس، معمولا مباحث مرتبط با روشهای حل مسائل برنامهریزی خطی را پوشش میدهد. یادگیری مباحث ارائه شده در درس تحقیق در عملیات 1 و دیگر درسهای مرتبط با آن، زمینه کسب مهارتهای مدیریتی و تحلیل مسائل مختلف برای تصمیمگیری مناسب را فراهم میکنند. این مباحث، ارتباط نزدیکی با مبحث بهینهسازی (پیدا کردن بهترین جواب در هر مسئله) دارند. در این مقاله، مهمترین مباحث تحقیق در عملیات 1 را به همراه حل چندین مثال متنوع و کاربردی آموزش میدهیم. در انتها، به معرفی نرمافزارهای کاربردی و بهترین منابع موجود برای یادگیری این درس میپردازیم.
تحقیق در عملیات چیست ؟
پژوهش عملیاتی، «تحقیق در عملیات» (Operation Research) یا به اختصار «OR»، یکی از شاخههای ریاضیات کاربردی و از مهمترین ابزارهای مورد استفاده در مهندسی صنایع است که به مطالعه روشهای تحلیل و حل مسئله میپردازد.
تحقیق در عملیات، اهمیت و کاربرد زیادی در مدیریت سازمانها و تسهیل فرآیندهای تصمیمگیری دارد. در این حوزه، مسائل به بخشهای کوچکتر تقسیم شده و طی چندین مرحله از پیش تعریف شده حل میشوند.

مراحل تحقیق در عملیات چه هستند ؟
فرآیند تحقیق در عملیات را میتوان به پنج مرحله کلی زیر تقسیمبندی کرد:
- تعریف مسئله
- مدلسازی ریاضی (نوشتن متغیرهای معرف مسئله واقعی به زبان ریاضی)
- به کارگیری مدل
- آزمایش راهحلها و بررسی موفقیت یا عدم موفقیت آنها
- حل مسئله در دنیای واقعی با توجه به خروجی مدل معتبر
تحقیق در عملیات، شباهت یا همپوشانی زیادی با دیگر روشهای تصمیمگیری نظیر تحلیل آماری، علم مدیریت، نظریه بازی، تئوری بهینهسازی، هوش مصنوعی و تحلیل شبکهای دارد.
فعالیت های تحقیق در عملیات چه هستند ؟
تمام پژوهشهای عملیاتی از سه ویژگی مشترک برخوردارند:
- بهینه سازی: هدف تحقیق در عملیات، دستیابی به بهترین عملکرد ممکن در شرایط موجود است. مقایسه و محدود کردن تعداد راه حلهای ممکن نیز از فرآیندهای بهینه سازی به شمار میرود.
- شبیه سازی: به منظور بررسی راه حلهای احتمالی، پیش از اجرای آنها بر روی مسئله واقعی، مدل معرف مسئله ساخته میشود.
- آمار و احتمالات: دادهها و الگوریتمهای ریاضی، به منظور فراهم آوردن دید بهتر نسبت مسئله و ریسکهای احتمالی آن مورد بررسی قرار میگیرند. فرآیندهای آماری و احتمالاتی، اعتبار پیشبینیها و راهحلهای احتمالی را بهبود میبخشند.
اهمیت تحقیق در عملیات چیست ؟
اهمیت تحقیق در عملیات، قدرت بالای آن در حل مسائل پیچیده حوزههای مختلف است. تحقیق در عملیات، چندین ابزار تصمیمگیری قدرتمند را در اختیار مدیران و دیگر افراد تصمیمگیرنده سازمانها قرار میدهد. کارشناسان این حوزه میتوانند به شرکتهای مختلف برای دستیابی به دادههای کاملتر برای رفع یک مشکل، در نظر گرفتن تمام گزینههای در دسترس، بررسی تمام خروجیهای احتمالی و تخمین ریسک کمک کنند.

قابلیتهای تحقیق در عملیات، بسیار بهتر از نرم افزارها و ابزارهای تحلیل داده معمولی هستند. این قابلیتها، از انعطافپذیری بالا برای سازگاری با فرآیندهای حوزههای مختلف بهره میبرند. به همین دلیل، کاربردهای تحقیق در عملیات به یک حوزه خاص محدود نمیشوند و گسترش بسیار زیادی دارند.
کاربرد تحقیق در عملیات چیست ؟
برخی از کاربردهای تحقیق در عملیات عبارت هستند از:
- مدیریت زمان و تهیه برنامه زمانبندی
- برنامهریزی شهری و کشاورزی
- برنامهریزی منابع سازمانی و مدیریت زنجیره تامین
- مدیریت انبار
- بهینهسازی شبکه و مهندسی
- بهینهسازی مسیر
- مدیریت ریسک
کاربردهای تحقیق در عملیات به موارد بالا محدود نمیشوند. حسابداری، ساخت و ساز، تاسیسات، اقتصاد، تولید، بازاریابی، منابع انسانی، تحقیق، توسعه و در هر حوزه دیگری که با تصمیمگیری همراه باشد، میتوان اثری از کاربردهای تحقیق در عملیات را مشاهده کرد.
روش های تحقیق در عملیات چه هستند ؟
روش های متعددی برای حل یک مسئله تصمیم گیری توسط اصول تحقیق در عملیات وجود دارند. از پرکاربردترین و متداولترین این روشها میتوان به موارد زیر اشاره کرد:
- برنامهریزی خطی
- سمپلکس
- حمل و نقل
- روش پله سنگ
- روش کمترین هزینه
- روش گوشه شمال غربی
- روش تقریبی وگل
- تخصیص
- عدد صحیح
- برنامهریزی غیر خطی
- برنامهریزی پویا
- نظریه صف
- نظریه بازی
- نظریه مارکوف
- شبیه سازی و تکنیک مونت کارلو
درس تحقیق در عملیات 1 معمولا مباحث مرتبط با حل مسائل برنامهریزی خطی به روشهای مختلف (مخصوصا روش ترسیمی، سیمپلکس، دوال سیمپلکس و حمل و نقل) میپردازد.
مراحل تحقیق در عملیات
در بخشهای قبلی، کلیات تحقیق در عملیات و مراحل موجود در آن آشنا شدید. در این بخش، هر یک از این مراحل را مورد بررسی قرار میدهیم.
مرحله اول: تعریف مسئله
مرحله اول تحقیق در عملیات، به تعریف اهداف و محدوده مسئله مورد نظر اختصاص دارد. این مرحله توسط تمام افراد حاضر در تیم تحقیق در عملیات صورت میگیرد. هدف اصلی، شناسایی سه المان مهم در مسئله تصمیمگیری است:
- توصیف روشهای تصمیمگیری و گزینههای جایگزین
- تعیین تابع هدف
- مشخص کردن محدودیتها
مرحله دوم: مدلسازی
هدف مرحله مدلسازی، تبدیل مسئله واقعی به روابط ریاضی است. اگر مدل به دست آمده با یکی از مدلهای استاندارد نظیر برنامهریزی خطی مطابقت داشته باشد، مسئله با الگوریتمهای موجود حل میشود. در صورت پیچیدگی روابط ریاضی، روشهای سادهسازی یا شبیهسازی به منظور حل مسئله مورد استفاده قرار میگیرند. در برخی از موارد، ترکیبی از مدلهای ریاضی، ابتکاری (تجربی) و شبیهسازی برای رسیدن به جواب استفاده میشود.

مرحله سوم: حل مدل
سادهترین مرحله تحقیق در عملیات، حل مدل با استفاده از الگوریتمهای بهینهسازی است. از مهمترین جنبههای این مرحله میتوان تحلیل حساسیت اشاره کرد. تحلیل حساسیت، به منظور تعیین اطلاعات اضافی در مورد نحوه تغییر جواب بهینه با تغییر پارامترهای مختلف مورد استفاده قرار میگیرد. در صورت عدم امکان تخمین مناسب پارامترهای مدل، اجرای تحلیل حساسیت، ضروری خواهد بود. در این شرایط، مطالعه رفتار جواب بهینه در همسایگی پارامترهای تخمینی از اهمیت بالایی برخوردار است.
مرحله چهارم: اعتبارسنجی مدل
تیم تحقیق در عملیات باید از صحیح بودن خروجیهای مدل و عدم مواجهه با جوابهای پیش بینی نشده اطمینان حاصل کند. به همین دلیل، در مرحله چهارم، اعتبار مدل و دقت پیش بینی آن مورد ارزیابی قرار میگیرد. یکی از روشهای متداول اعتبارسنجی مدل، گرفتن خروجیهای مختلف از آن و مقایسه این خروجیها با دادههای قبلی است. اگر مدل در شرایط مشابه، عملکرد یکسانی نسبت به عملکرد قبلی خود داشته باشد، اعتبار آن تایید میشود.
به طور کلی، هیچ تضمینی برای تکرار رفتار مدل در آینده وجود ندارد. به علاوه، مدلها معمولا از روی دادههای قبلی ساخته میشوند. به همین دلیل، در اکثر موارد، دادههای جدید دادههای قدیمی مطابقت دارند. اگر مدل، بیانگر یک سیستم جدید (سیستمی با دادههای ناموجود) باشد، امکان مقایسه آن با سیستمهای قبلی وجود نخواهد داشت. در این حالت، میتوان از شبیهسازی برای اعتبارسنجی مدل ریاضی استفاده کرد.
مرحله پنجم: اجرا
در مرحله آخر تحقیق در عملیات، راه حل ارائه شده توسط مدل معتبر به مسئله واقعی اعمال میشود. این مرحله شامل تبدیل جوابهای بهینه به دستورالعملهای قابل درک برای مدیران و تصمیمگیرندگان است.
درس تحقیق در عملیات 1 چیست ؟
درس تحقیق در عملیات 1 یکی از دروس اصلی و تخصصی رشتههای مدیریت و مهندسی صنایع است. به دلیل اهمیت بالا و کاربردهای گسترده تحقیق در عملیات، مبحث مرتبط با آن معمولا در مقاطع کارشناسی و کارشناسی ارشد رشتههای مختلف، تحت عناوینی نظیر تحقیق در عملیات 1، تحقیق در عملیات 2، تحقیق در عملیات 3، تحقیق در عملیات پیشرفته و غیره تدریس میشوند.

از سرفصلهای درس تحقیق در عملیات 1 میتوان به موارد زیر اشاره کرد:
- معرفی تاریخچه، مبانی، تعاریف و اهداف تحقیق در عملیات
- مدلسازی ریاضی مسائل تحقیق در عملیات
- برنامهریزی خطی و روشهای آن (مخصوصا روش سیمپلکس و حمل و نقل)
- حالتهای خاص مسائل برنامهریزی خطی
- آنالیز حساسیت
برنامهریزی خطی در تحقیق در عملیات 1
تصویر زیر را در نظر بگیرید. این تصویر، محل قرارگیری یک شرکت پستی و شش خانه را نمایش میدهد. شرکت پست در نقطه A و خانهها در نقطههای U تا Z قرار دارند. فاصله بین هر دو نقطه بر روی خط اتصال آنها نوشته شده است. کارمند پست باید شش مرسوله پستی را در یک روز کاری به این شش خانه برساند.

کارمند پست قصد دارد برای به حداقل رساندن هزینه سوخت و زمان، کوتاهترین مسیر را انتخاب کند. او در نهایت، با محاسبه حالتهای مختلف، کوتاهترین مسیر را به دست میآورد. به روش مورد استفاده برای انتخاب کوتاهترین مسیر، برنامهریزی خطی میگویند. در ادامه، برنامهریزی خطی و اجزای آن را به کمک این مثال مورد بررسی قرار میدهیم.
تعریف برنامهریزی خطی چیست ؟
«برنامهریزی خطی» (Linear Programming) یا «بهینه سازی خطی» (Linear Optimization)، از روشهای متداول تحقیق در عملیات 1 است که به منظور بهینهسازی تابع هدف خطی با محدودیتهای خطی مورد استفاده قرار میگیرد. زمانی که در یک مسئله تصمیمگیری راجع به بهینه سازی صحبت میکنیم، منظور ما به حداکثر رساندن خروجی تابع هدف (مانند سود) یا به حداقل رساندن خروجی تابع هدف (مانند زیان) است. برنامهریزی خطی به ما کمک میکند تا رابطه پیچیده بین چند تابع خطی را به سادگی بیان کرده و نقاط بهینه آنها را پیدا کنیم.
در مثال شرکت پست، هدف پستچی، تحویل تمام شش مرسوله در زمان مشخص و با طی کردن کمترین مسیر ممکن بود. فرآیند انتخاب بهترین مسیر در این مثال، همان تحقیق در عملیات 1 است. مدل خطی مسیر تحویل مرسولههای پستی، سیستم مورد بررسی در مسئله تصمیمگیری را نشان میدهد. با وجود شباهتهای این مدل به واقعیت، سادهسازی قابل توجهی بر روی آن صورت گرفته است؛ چراکه در دنیای واقعی، تمام مسیرها کاملا مستقیم نیستند. البته توجه داشته باشید که اگر این سادهسازی انجام نمیگرفت، امکان حل مسئله تحقیق در عملیات 1 به روش برنامهریزی خطی فراهم نمیشد.
فرمول بندی مسئله برنامهریزی خطی
به منظور استفاده از روش برنامهریزی خطی برای دستیابی به جواب بهینه در مسائل تحقیق در عملیات، باید هدف مسئله و محدودیتهای موجود در آن را به زبان ریاضی نوشت. این کار با عنوان فرموله کردن مسئله شناخته میشود. فرموله کردن مسئله برنامهریزی، معمولا طی مراحل زیر انجام میشود:
- شناسایی متغیرهای مسئله
- نوشتن تابع هدف
- نوشتن محدودیتها
- بیان محدود غیر منفی بودن متغیرها
برای درک روند فرموله کردن مسئله، یک کارخانه شکلاتسازی را در نظر بگیرید. این کارخانه، تنها دو نوع شکلات (شکلات A و شکلات B) را تولید میکند. برای ساخت هر دو شکلات، فقط دو ماده اولیه (شیر و شکلات) مورد استفاده قرار میگیرند. مواد اولیه مورد نیاز برای ساخت هر نوع شکلات عبارت هستند از:
- شکلات A: یک واحد شیر و سه واحد شکلات
- شکلات B: یک شیر و دو واحد شکلات
آشپزخانه واحد تولید کارخانه، مجموعا پنج واحد شیر و 12 واحد شکلات دارد. سود کارخانه از فروش هر محصول برابر است با:
- سود شکلات A: شش واحد پول
- سود شکلات B: پنج واحد پول
هدف کارخانه، دستیابی به حداکثر سود ممکن با استفاده از منابع موجود و تولید شکلاتهای A و B است. کارخانه با تولید چه تعداد شکلات A و چه تعداد شکلات B به این هدف خواهد رسید؟
یکی از بهترین روشهای ممکن برای درک بهتر مسئله و فرموله کردن آن، ساخت جدول اطلاعات موجود است. جدول زیر، اطلاعات این مسئله را نمایش میدهد.
| شیر | شکلات | سود فروش | |
| شکلات A | 1 | 3 | 6 |
| شکلات B | 1 | 2 | 5 |
| جمع | 5 | 12 |
مرحله بعد، اختصاص متغیر به اطلاعات مسئله است. در اینجا، تعداد تولید شکلاتهای A را با X، تعداد تولید شکلاتهای B را با Y و سود حاصل از فروش مجموع شکلاتها را با Z مشخص میکنیم. بر این اساس، هدف کارخانه، به حداکثر رساندن مقدار متغیر Z است. سود هر X واحد شکلات A برابر 6 و سود هر Y واحد شکلات B برابر 5 است. اگر بخواهیم این جملات را به زبان ریاضی بنویسیم، به تابعی مشابه زیر میرسیم:
$$
Max Z = 6X + 5Y
$$
به تابع بالا، تابع هدف میگویند. مسئله مورد بررسی در اینجا، یک مسئله حداکثرسازی (ماکزیمم سازی) است. در صورتی که مقادیر عددی X و Y را به دست بیاوریم، میتوانیم بگوییم که حداکثر سود ممکن برای کارخانه چقدر خواهد بود.
نکته: برای نمایش تابع هدف در مسائل تحقیق در عملیات، معمولا از حرف Z استفاده میشود.
به نظر شما، نوشتن تابع هدف برای حل مسئله کفایت میکند. در دستگاه معادلات خطی، حل یک معادله با دو مجهول ممکن نیست. بنابراین، به معادلات بیشتری برای حل مسئله تصمیمگیری نیاز داریم. این معادلات با عنوان محدودیتهای مسئله شناخته میشوند. محدودیتهای کارخانه شکلاتسازی، مقدار مواد اولیه موجود در آشپزخانه آن است. به مواد اولیه در این مثال، منابع در دسترس میگویند. در حالت کلی، هر کارخانهای تمایل دارد بیشترین تعداد محصول ممکن را تولید کند و با فروش تمام آنها به سود بیشتری برسد. با این وجود، در واقعیت، منابع در دسترس محدود هستند.
برای نوشتن محدودیت منابع به زبان ریاضی، به جدول رجوع میکنیم. مجموع شیر در دسترس برابر 5 واحد، مقدار شیر مورد نیاز برای تولید شکلات A برابر 1 و مقدار شیر مورد نیاز برای تولید شکلات B برابر 1 است. از اینرو، میزان شیر مورد استفاده نباید از 5 واحد بیشتر شود. رابطه ریاضی این جمله عبارت است از:
$$
1X + 1Y \leq 5
$$
تعداد حداکثر شکلات موجود نیز برابر 12 واحد است. تولید هر واحد شکلات A نیازمند 3 واحد شکلات و تولید هر واحد شکلات B نیازمند 2 واحد شکلات است. در مجموع، میزان شکلات مصرفی در فرآیند تولید نباید از 12 عبور کند. به زبان ریاضی، میتوانیم بگوییم:
$$
3X + 2Y \leq 12
$$
تا به اینجا، دو محدودیت را نوشتیم. با داشتن این دو محدودیت، امکان به دست آوردن مقادیر X و Y فراهم میشود. اما محدودیتهای تعریف شده توسط ما کافی نیستند. به عنوان مثال، ممکن است جواب X و Y به صورت اعشاری یا منفی باشند (فقط اعداد صحیح در این مسئله قابل قبول هستند). مطمئنا هیچ کارخانهای نصف شکلات یا یک سوم شکلات را تولید نمیکند. به علاوه، منفی شدن تعداد شکلاتهای تولیدی نیز امکانپذیر نیست. منفی نبودن متغیرها را به صورت زیر مینویسیم:
$$
X \geq 0, \space Y\geq 0
$$
اکنون میتوانیم مسئله حداکثرسازی سود کارخانه از فروش شکلاتهای A و B را به روش برنامهریزی خطی حل کنیم. مراحلی که تا به اینجا انجام دادیم، فرموله سازی یک مسئله واقعی و تبدیل آن به مدل ریاضی بود.

شرطهای مسئله برنامهریزی خطی
از شرطهای یک مسئله برنامهریزی خطی میتوان به موارد زیر اشاره کرد:
- خطی بودن: رابطه بین یا چند متغیر در تابع هدف و محدودیتها باید به صورت خطی باشد.
- محدود یا نامحدود بودن: امکان اعمال ورودیهای محدود یا نامحدود و گرفتن خروجیهای محدود یا نامحدود وجود داشته باشد. در صورت نامحدود بودن ضرایب تابع هدف، رسیدن به جواب بهینه ممکن نیست.
- غیر منفی بودن: مقدار متغیرها باید مثبت یا صفر باشد.
پارامترهای مسئله برنامهریزی خطی
متغیرهای تصمیم، تابع هدف و محدودیتها مهمترین پارامترهای موجود در یک مسئله برنامهریزی خطی هستند:
- متغیرهای تصمیم: خروجی نهایی تابع، بر اساس متغیرهای تصمیم تعیین میشود. به منظور حل هر مسئله برنامهریزی خطی، ابتدا باید متغیرهای تصمیم آن را پیدا کرد. در مثال کارخانه شکلاتسازی، تعداد شکلات A و B، متغیرهای تصمیم بودند.
- تابع هدف: هدف مسئله تصمیمگیری در غالب تابع هدف بیان میشود. در مثال کارخانه شکلاتسازی، هدف، حداکثرسازی سود فروش بود.
- محدودیتها: عوامل تاثیرگذار بر روی تصمیم نهایی به صورت محدودیت وارد مسئله میشوند. این عوامل، معمولا بازه مقادیر متغیرهای تصمیم را محدود میکنند. در مثال کارخانه شکلاتسازی، میزان منابع در دسترس (شیر و شکلات)، محدودیتهای مسئله بودند.
روش ترسیمی حل مسئله برنامه ریزی خطی در تحقیق در عملیات 1
روشهای متعددی برای حل مسائل برنامهریزی خطی وجود دارند. از سادهترین و ابتداییترین روشهای حل مسائل تحقیق در عملیات، میتوان به روش ترسیمی اشاره کرد. این روش برای حل مسائل برنامهریزی خطی دو متغیره مورد استفاده قرار میگیرد.
در برنامهریزی خطی به روش ترسیمی، نامساویهای مربوط به محدودیتها در یک دستگاه مختصات دو بعدی رسم میشوند. با رسم تمام محدودیتها، یک ناحیه جواب موجه به وجود میآید. این ناحیه، جوابهای قابل قبول و احتمالی مدل را نمایش میدهد. طبیعتا جواب بهینه نیز در این ناحیه قرار دارد.
حل مثال تحقیق در عملیات 1 به روش ترسیمی
بهترین راه برای درک روش ترسیمی برنامهریزی خطی، حل مثال است. یک کشاورز با زمینی به وسعت 110 هکتار را در نظر بگیرید. این کشاورز میخواهد در زمین خود، گندم و جو کشت کند. جدول زیر اطلاعات مرتبط با هزینه، سود خالص و نیروی کار مورد برای کشت گندم و جو در هر یک هکتار را نمایش میدهد.
| نوع محصول | هزینه | سود خالص | نیروی کار روزانه |
| گندم | 100 | 50 | 10 |
| جو | 200 | 120 | 30 |
بودجه کشاورز برابر 10000 (10 هزار) واحد و نیروی کار در دسترس برای مجموع روزهای فصل کاشت برابر 1200 نفر است. کشاورز باید چه مقدار از زمین خود را گندم و چه مقدار را جو بکارد تا به حداکثر سود ممکن برسد؟
مرحله اول: تعیین متغیرهای تصمیم
مساحت کشت گندم و جو، پارامترهای تاثیرگذار بر روی سود نهایی هستند. به همین دلیل، متغیرهای تصمیم این مسئله به صورت زیر نوشته میشوند:
- X: مساحت کشت گندم به هکتار
- Y: مساحت کشت جو به هکتار
مرحله دوم: نوشتن تابع هدف
سود حاصل از کشت هر هکتار گندم (X) برابر 50 و سود حاصل از کشت هر هکتار جو (Y) برابر 120 است. هدف کشاورز این است که سود حاصل از مجموع فروش دو محصول به حداکثر برسد. بنابراین، برای تابع هدف خواهیم داشت:
$$
\begin{aligned}
&\text { Max } Z=50 X+120 Y \\
\end{aligned}
$$
مرحله سوم: نوشتن محدودیتها
سه محدودیت اختصاصی برای این مسئله داریم. محدودیت اول، به میزان بودجه کشاورز ارتباط دارد. مجموع هزینههای کشت دو محصول نباید از بودجه بیشتر باشد. فرم ریاضی این محدودیت عبارت است از:
$$
\begin{aligned}
100X+200Y \leq 10000\\
\end{aligned}
$$
محدودیت دوم، به تعداد نیروی کار در هر روز مربوط میشود. مجموع نیروی کار در دسترس نمیتواند بیشتر از 1200 نفر باشد. به زبان ریاضی:
$$
\begin{aligned}
10X+30Y \leq 1200\\
\end{aligned}
$$

محدودیت سوم به مسئله مجموع مساحت زمین قابل کشت باز میگردد. این مساحت نمیتواند بیشتر از 110 هکتار باشد:
$$
\begin{aligned}
X+Y \leq 110\\
\end{aligned}
$$
مرحله چهارم: محدودیت غیر منفی بودن متغیرها
در نهایت، محدودیت غیر منفی بودن متغیرهای تصمیم را مینویسیم:
$$
X \geq 0, \space Y\geq 0
$$
اگر همه این فرمولها را در کنار یکدیگر قرار دهیم، مدل ریاضی مسئله به دست میآید:
$$
\begin{aligned}
\text { Max } &Z=50 X+120 Y \\
s.t.\space & 100X+200Y \leq 10000\\
&10X+30Y \leq 1200\\
&X+Y \leq 110\\
&X \geq 0, \space Y\geq 0
\end{aligned}
$$
مرحله پنجم: رسم محدودیتها در دستگاه مختصات
پیش از رسم محدودیتها در دستگاه مختصات، توجه داشته باشید که به دلیل وجود محدود غیر منفی بودن متغیرها، محدوده موجه در ربع اول دستگاه مختصات قرار میگیرد. برای رسم آسان محدودیتها میتوانیم آنها را ساده کنیم. به این ترتیب، به سه نامساوی زیر میرسیم:
$$
\begin{aligned}
&X+2Y \leq 100\\
&X+3Y \leq 120\\
&X+Y \leq 110\\
\end{aligned}
$$
تصویر زیر، خطوط مربوط به معادلههای بالا در دستگاه مختصات را نمایش میدهد.
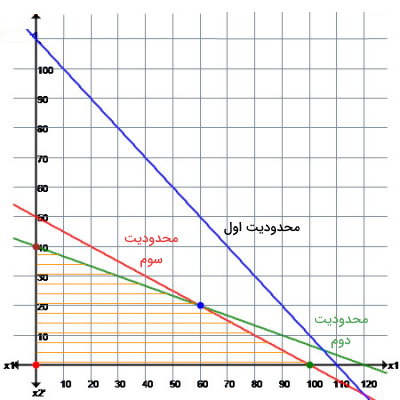
ناحیه مشترک بین هر محدودیت به صورت هاشور مشخص شده است. جواب بهینه، در یکی از گوشههای ناحیه بالا (محل تقاطع خطوط) قرار دارد. مختصات این گوشهها را پیدا میکنیم و درون تابع هدف قرار میدهیم. مختصات دارای بیشترین مقدار، جواب مسئله بیشینهسازی سود است. با بررسی نقاط گوشه و قرار دادن آنها در تابع هدف، متوجه خواهید شد که مختصات (60,20)، بیشترین خروجی را در تابع هدف دارد:
$$
Max \space Z =(50 \times 60) + (120\times20)
$$
$$
Max \space Z =5400
$$
همانطور که قبلا اشاره کردیم، روش ترسیمی برای مسائل ساده با دو متغیر کاربرد دارد. در صورت افزایش تعداد متغیرها، حل مسئله به روش ترسیمی پیچیده میشود.
روش سیمپلکس در تحقیق در عملیات 1
سیمپلکس، یکی از پرکاربردین و محبوبترین روشهای حل مسائل برنامهریزی خطی است. بسیاری از مباحث مرتبط با روش سیمپلکس به طور در درس تحقیق در عملیات 1 مورد بررسی قرار میگیرند. این روش، طی یک فرآیند تکراری، جوابهای گوشه ناحیه موجه را پیدا میکند و با هر تکرار، به جواب بهینه نزدیکتر میشود.
یکی از نکات مهم در حل مسائل برنامهریزی خطی به روش سیمپلکس، تبدیل تابع هدف و محدودیتها به فرم استاندارد است. در فرم استاندارد سیمپلکس، تابع هدف به صورت تابع بیشنهسازی و نامساویها به صورت معادله نوشته میشوند.
حل مثال تحقیق در عملیات 1 به روش سیمپلکس
در این بخش، مسئله زیر را توسط الگوریتم سیمپلکس حل میکنیم و مفاهیم مرتبط با این الگوریتم را توضیح میدهیم:
$$
\begin{aligned}
&\text { Maximize } z=f(x, y)=3 x+2 y \\
&\text { subject to: } 2 x+y \leq 18 \\
&2 x+3 y \leq 42 \\
&3 x+y \leq 24 \\
&x \geq 0, y \geq 0
\end{aligned}
$$
مرحله اول: نامگذاری متغیرها
برای شروع حل، عنوان متغیر x را به X1 و عنوان متغیر y را به X2 تغییر میدهیم. این دو متغیر، متغیرهای تصمیم هستند. برای متغیرهای کمکی (کمبود، مازاد و مصنوعی) از عنوانهای S2 ،S1 و غیره استفاده خواهیم کرد.
مرحله دوم: نرمالسازی محدودیتها و تابع هدف
طی نرمالسازی محدودیتها، نامساویها را با اضافه کردن متغیرهای کمبود، مازاد و مصنوعی به معادله تبدیل میکنیم. جدول زیر، نوع متغیر مورد استفاده را با توجه به نوع نامساوی نمایش میدهد.
| نوع نامساوی | نحوه وارد کردن متغیر برای تبدیل |
| بزرگتر مساوی ≤ | متغیر مصنوعی + متغیر مازاد - |
| مساوی = | متغیر مصنوعی + |
| کوچکتر مساوی ≥ | متغیر کمبود + |
در مثال مورد بررسی، تمام محدودیتها به صورت کوچکتر مساوی هستند. به همین دلیل، نامساویها به شکل زیر نوشته میشوند:
$$
\begin{gathered}
2 \cdot X_{1}+X_{2}+X_{3}=18 \\
2 \cdot X_{1}+3 \cdot X_{2}+X_{4}=42 \\
3 \cdot X_{1}+X_{2}+X_{5}=24
\end{gathered}
$$
در انتها، متغیرهای کمکی را به تابع هدف اضافه میکنیم و با بردن تمام متغیرها (تصمیم و کمکی) به سمت دیگر تابع، آن را برابر صفر قرار میدهیم:
$$
Z-3 \cdot X_{1}-2 \cdot X_{2}-0 \cdot X_{1}-0 \cdot X_{2}-0 \cdot X_{3}=0
$$
مرحله سوم: تشکیل جدول سیمپلکس
پس از نرماله کردن محدودیتها و تابع هدف، باید ضرایب آنها را وارد یک جدول کنیم. این جدول با عنوان جدول اولیه سیمپلکس شناخته میشود. پایینترین ردیف جدول، به ضرایب تابع هدف اختصاص دارد. به ازای هر محدودیت، یک ردیف به بالای ردیف ضرایب تابع هدف اضافه میکنیم. در بالاترین ردیف، عنوان متغیرهای تصمیم و متغیرهای کمکی را مینویسیم. بر این اساس، ساختار جدول اولیه سیمپلکس برای مثال مورد بررسی ما به شکل زیر در میآید.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 18 | 0 | 0 | 1 | 1 | 2 | S1 |
| 42 | 0 | 1 | 0 | 3 | 2 | S2 |
| 24 | 1 | 0 | 0 | 1 | 3 | S3 |
| 0 | 0 | 0 | 0 | 2- | 3- | Z |
به ستون R.H.S، اعداد سمت راست جدول سیمپلکس میگویند. متغیرهای S نیز معمولا با عنوان متغیرهای اساسی شناخته میشوند. هدف اول در روش سیمپلکس، پیدا کردن سطر و ستون کلیدی است.
مرحله چهارم: پیدا کردن ستون کلیدی
شناسایی ستون کلیدی، برای تعیین تاثیرگذارترین متغیر ضروری است. میزان تاثیرگذاری متغیر، به ضریب آن در تابع هدف بستگی دارد. از اینرو، در ردیف ضرایب تابع هدف، منفیترین عدد را انتخاب کرده و ستون دربرگیرنده آن را به عنوان ستون کلیدی در نظر میگیریم.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 18 | 0 | 0 | 1 | 1 | 2 | S1 |
| 42 | 0 | 1 | 0 | 3 | 2 | S2 |
| 24 | 1 | 0 | 0 | 1 | 3 | S3 |
| 0 | 0 | 0 | 0 | 2- | 3- | Z |
مرحله پنجم: پیدا کردن سطر و عدد کلیدی
برای پیدا کردن سطر و عدد کلیدی، اعداد ستون R.H.S را بر اعداد ستون کلیدی تقسیم میکنیم (به غیر از سطر ضرایب تابع هدف). حاصل تقسیم این اعداد از سطر S1 تا S3 پایین برابر است با:
9 = 2 ÷ 18
21 = 2 ÷ 42
8 = 3 ÷ 24
از بین تقسیمهای بالا، کوچکترین عدد مربوط به تقسیم اعداد سطر S3 است. این سطر را به عنوان سطر کلیدی در نظر گرفته میشود.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 18 | 0 | 0 | 1 | 1 | 2 | S1 |
| 42 | 0 | 1 | 0 | 3 | 2 | S2 |
| 24 | 1 | 0 | 0 | 1 | 3 | S3 |
| 0 | 0 | 0 | 0 | 2- | 3- | Z |
عدد محل تقاطع سطر و ستون کلیدی (3)، اولین عدد کلیدی در این جدول سیمپلکس است.
مرحله ششم: وارد کردن متغیر تصمیم و یکه کردن ستون کلیدی
در مرحله بعد، ابتدا متغیر ستون کلیدی (X1) را به جای متغیر سطر کلیدی (S3) قرار میدهیم. سپس، تمام اعداد سطر کلیدی را به عدد کلیدی تقسیم میکنیم.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 18 | 0 | 0 | 1 | 1 | 2 | S1 |
| 42 | 0 | 1 | 0 | 3 | 2 | S2 |
| 24/3 | 1/3 | 0/3 | 0/3 | 1/3 | 3/3 | X1 |
| 0 | 0 | 0 | 0 | 2- | 3- | Z |
با این کار، عدد کلیدی به یک تبدیل میشود.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 18 | 0 | 0 | 1 | 1 | 2 | S1 |
| 42 | 0 | 1 | 0 | 3 | 2 | S2 |
| 8 | 1/3 | 0 | 0 | 1/3 | 1 | X1 |
| 0 | 0 | 0 | 0 | 2- | 3- | Z |
مهمترین مرحله در اجرای الگوریتم سیمپلکس، بهروزرسانی و یکه کردن دادههای جدول است. به این منظور باید تمام اعداد ستون کلیدی (به غیر از عدد کلیدی) صفر شوند. برای این کار، عدد ستون کلیدی در سطر S1 را انتخاب کرده (عدد 2) و آن را در 1- ضرب میکنیم. حاصلضرب این دو عدد، 2- است. اعداد سطر کلیدی را در 2- ضرب میکنیم.
| 8×(2-) | 1/3×(2-) | 0×(2-) | 0×(2-) | 1/3×(2-) | 1×(2-) |
نتیجه این ضرب برابر است با:
| 16- | 2/3- | 0 | 0 | 2/3- | 2- |
حاصلضرب را با سطر انتخابی (S1) جمع میکنیم:
| 16- | 2/3- | 0 | 0 | 2/3- | 2- |
+
| 18 | 0 | 0 | 1 | 1 | 2 |
=
| 2 | 2/3- | 0 | 1 | 1/3 | 0 |
حاصل جمع بالا را در جدول سیمپلکس قرار میدهیم.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 2 | 2/3- | 0 | 1 | 1/3 | 0 | S1 |
| 42 | 0 | 1 | 0 | 3 | 2 | S2 |
| 8 | 1/3 | 0 | 0 | 1/3 | 1 | X1 |
| 0 | 0 | 0 | 0 | 2- | 3- | Z |
این کار مرحله را برای سطر S2 و Z تکرار میکنیم. در انتهای این مرحله، جدول سیمپلکس به شکل زیر در میآید.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 2 | 2/3- | 0 | 1 | 1/3 | 0 | S1 |
| 26 | 2/3- | 1 | 0 | 7/3 | 0 | S2 |
| 8 | 1/3 | 0 | 0 | 1/3 | 1 | X1 |
| 24 | 1 | 0 | 0 | 1- | 0 | Z |
همانطور که مشاهده میکنید، ستون کلیدی یکه شد. شرط بهینگی در روش سیمپلکس، منفی نبودن اعداد سطر ضرایب تابع هدف است. در جدول بالا، هنوز یک ضریب منفی (1-) در سطر ضرایب تابع هدف وجود دارد. به همین دلیل، این جدول به عنوان جدول دوم سیمپلکس در نظر گرفته میشود.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 2 | 2/3- | 0 | 1 | 1/3 | 0 | S1 |
| 26 | 2/3- | 1 | 0 | 7/3 | 0 | S2 |
| 8 | 1/3 | 0 | 0 | 1/3 | 1 | X1 |
| 24 | 1 | 0 | 0 | 1- | 0 | Z |
باید ستون مربوط به آن عدد منفی را به عنوان ستون کلیدی انتخاب کرده و مراحل قبلی را برای تعیین سطر کلیدی، نرماله کردن سطر کلیدی و یکه کردن ستون کلیدی تکرار کنیم. با تکرار این مراحل، به جدول زیر میرسیم:
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 6 | 2- | 0 | 3 | 1 | 0 | X2 |
| 12 | 4 | 1 | 7- | 0 | 0 | S2 |
| 6 | 1 | 0 | 1- | 0 | 1 | X1 |
| 30 | 1- | 0 | 3 | 0 | 0 | Z |
در سطر ضرایب تابع هدف، هنوز یک عدد منفی باقیمانده است. در نتیجه، جدول بالا را به عنوان جدول سوم سیمپلکس در نظر میگیریم و مراحل قبلی را تکرار میکنیم.
| R.H.S | S3 | S2 | S1 | X2 | X1 | |
| 12 | 0 | 1/2 | 1/2- | 1 | 0 | X2 |
| 3 | 1 | 1/4 | 7/4- | 0 | 0 | S3 |
| 3 | 0 | 1/4- | 3/4 | 0 | 1 | X1 |
| 33 | 0 | 1/4 | 5/4 | 0 | 0 | Z |
در سطر ضرایب تابع هدف جدول بالا، هیچ عدد منفی وجود ندارد. به این ترتیب، شرط بهینگی ارضا شده است. عدد سمت راست در سطر تابع هدف (عدد 33)، مقدار بهینه (بیشینه) تابع را نمایش میدهد. اعداد سمت راست سطرهای X1 و X2 (اعداد 3 و 12)، مقدار بهینه متغیرهای تصمیم هستند. اگر به خروجی تابه هدف در مرحله دقت کنید، متوجه خواهید شد که این خروجی با هر تکرار افزایش مییابد. در واقع، در هر مرحله، یک نقطه گوشه پیدا میشود و بهینگی آن مورد بررسی قرار میگیرد.

مراحل اجرای الگوریتم سیمپلکس
مراحل کلی اجرای الگوریتم سیمپلکس عبارت هستند از:
- نوشتن تابع هدف و محدودیتهای مسئله
- نوشتن فرم استاندارد مسئله (بخش بعدی مقاله)
- اضافه کردن متغیرهای مصنوعی (در صورت وجود محدودیتهای مساوی یا بزرگتر مساوی در فرم اولیه مسئله)
- ایجاد جدول سیمپلکس اولیه (نوشتن ضرایب تابع هدف و محدودیتها)
- شناسایی منفیترین مقدار در ردیف ضرایب تابع هدف برای پیدا کردن ستون کلیدی (تعیین متغیر ورودی)
- تقسیم ضرایب ستون سمت راست جدول بر اعداد ستون کلیدی و انتخاب ردیف دارای کوچکترین کسر مثبت به عنوان سطر کلیدی (تعیین متغیر خروجی)
- شناسایی عدد کلیدی در محل تقاطع ستون و ردیف کلیدی
- تقسیم تمام اعداد سطر کلیدی بر عدد کلیدی و اجرای محورگیری برای صفر کردن دیگر اعداد ستون کلیدی
- بررسی شرط بهینگی
- تکرار مراحل 4 تا 9 در صورت عدم برقرار بودن شرط بهینگی یا توقف حل مسئله در صورت برقرار بودن شرط بهینگی
- تعیین جواب بهینه از روی عدد سمت راست در ردیف ضرایب تابع هدف
فرم استاندارد مسئله برنامه ریزی خطی
اولین مرحله در حل مسائل برنامه ریزی خطی که معمولا در درس تحقیق در عملیات 1 و مبحث الگوریتم سیمپلکس آموزش داده میشود، نوشتن مسائل به صورت استاندارد است. به طور کلی، برای استاندارد کردن یک مسئله برنامهریزی خطی، باید به نکات زیر توجه کرد:
- بیشینه بودن تابع هدف
- مثبت بودن مقادیر سمت راست نامساویها
- تبدیل نامساویها به معادله
- غیر منفی بودن تمام متغیرها
در بسیاری از مسائل، شرایط بالا یا برخی از آنها برقرار نیستند. در این شرایط، باید با استفاده از روشهای مخصوص، فرم مسئله را تغییر داد:
- تبدیل کمینه سازی به بیشینه سازی
- به منظور تبدیل مسئله از کمینهسازی (Min) به بیشینهسازی (Max) و بالعکس، باید تابع هدف را در عدد (1-) ضرب کرد.
- تبدیل نامساوی به معادله
- تبدیل نامساوی به معادله با اضافه کردن یا کم کردن متغیرهای کمکی انجام میگیرد. برای تبدیل کوچکتر مساوی (≥) به معادله (=)، سمت چپ نامساوی با یک متغیر کمبود جمع میشود. راهحل تبدیل بزرگتر مساوی (≤) به معادله نیز، کم کردن یک متغیر مازاد از سمت چپ نامساوی است.
مثال نوشتن مسئله برنامه ریزی خطی به فرم استاندارد
در این بخش، نحوه نوشتن مسائل برنامهریزی خطی به فرم استاندارد را با انجام دو مثال آموزش میدهیم.
مثال 1: نوشتن فرم استاندارد مسئله بیشینهسازی
برای مثال اول، مسئله زیر را در نظر بگیرید:
$$
\begin{array}{ll}
\operatorname{Max} & Z=4 x_{1}+3 x_{2} \\
\text { s.t. } & x_{1}+x_{2} \leq 3 \\
& 2 x_{1}-x_{2} \leq 3 \\
& x_{1} \leq 4 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
مسئله بالا از نوع بیشینهسازی است. در نتیجه، نیازی به تبدیل نوع بهینهسازی تابع هدف وجود ندارد. تنها تغییر مورد نیاز برای تابع هدف، انتقال تمام متغیرها از سمت چپ به سمت راست آن است:
$$
\begin{array}{ll}
\operatorname{Max} & Z - 4 x_{1} - 3 x_{2} = 0
\end{array}
$$
در این مسئله، سه محدودیت وجود دارد که تمامی آنها، از نوع کوچکتر مساوی هستند. بنابراین، برای این سه محدودیت، سه متغیر کمبود s2 ،s1 و s3 تعریف کرده و هر یک را به سمت چپ یک محدودیت اضافه میکنیم:
$$
\begin{array}{ll}
\text { s.t. } & x_{1}+x_{2} + s _ {1} = 3 \\
& 2 x_{1}-x_{2} + s _ {1} = 3 \\
& x_{1} + s _ {1} = 4 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
اکنون، پنج متغیر (متغیرهای تصمیم x1 و x2 و متغیرهای کمکی s2 ،s1 و s3) در مسئله وجود دارند که همگی باید غیر منفی باشند. در نتیجه، محدودیت زیر را نیز به فرم استاندارد اضافه میکنیم:
$$
x_{1}, x_{2},s_{1}, s_{2},s_{3} \geq 0
$$
در نهایت، فرم استاندارد مسئله به شکل زیر در میآید:
$$
\begin{array}{ll}
\operatorname{Max} & Z-4 x_{1}-3 x_{2}=0 \\
\text { s.t. } & x_{1}+x_{2}+s_{1}=3 \\
& 2 x_{1}-x_{2}+s_{2}=3 \\
& x_{1}+s_{3}=4 \\
& x_{1}, x_{2}, s_{1}, s_{2}, s_{3} \geq 0
\end{array}
$$
مثال 2: نوشتن فرم استاندارد مسئله کمینهسازی
مسئله زیر در نظر بگیرید:
$$
\begin{array}{ll}
\operatorname{Min} Z= & 2 x_{1}+x_{2} \\
\text { st. } \quad & 3 x_{1}+x_{2} \geq 3 \\
& 4 x_{1}+3 x_{2} \geq 6 \\
& x_{1}+2 x_{2} \leq 3 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
مسئله بالا، یک مسئله کمینهسازی با سه محدودیت است. از اینرو، برای نوشتن فرم استاندارد، ابتدا باید تابع هدف را در عدد (1-) ضرب کنیم تا مسئله به یک مسئله بیشینهسازی تبدیل شود:
$$
\begin{array}{ll}
\operatorname{Max} -Z= & -2 x_{1}-x_{2} \\
\end{array}
$$
در قدم بعدی، عبارتهای سمت راست را به سمت چپ میبریم:
$$
\begin{array}{ll}
\operatorname{Max} -Z + 2 x_{1} + x_{2} = 0 \\
\end{array}
$$
محدودیتهای اول و دوم از نوع بزرگتر مساوی هستند. برای تبدیل این نامساویها به معادله، دو متغیر مازاد (s1 و s2) تعریف کرده و آنها را از عبارتهای سمت چپ کم میکنیم:
$$
\begin{aligned}
\quad 3 x_{1}+x_{2}-s_{1}=3 \\
4 x_{1}+3 x_{2}-s_{2}=6 \\
\end{aligned}
$$
محدودیت سوم، یک نامساوی از نوع کوچکتر مساوی است. متغیر کمبود (s3) را برای این محدودیت تعریف کرده و آن را به عبارتهای سمت چپ اضافه میکنیم:
$$
\begin{aligned}
x_{1}+2 x_{2}+s_{3}=3 \\
\end{aligned}
$$
سپس، باید محدودیت غیر منفی بودن تمام متغیرهای تصمیم و متغیرهای کمکی را بنویسیم:
$$
\begin{aligned}
x_{1}, x_{2}, s_{1}, s_{2}, s_{3} \geq 0
\end{aligned}
$$
در انتها، فرم استاندارد مسئله به شکل زیر در میآید:
$$
\begin{aligned}
{Max}& -Z+2 x_{1}+x_{2}=0 \\
\text { s.t. } & 3 x_{1}+x_{2}-s_{1}=3 \\
&4 x_{1}+3 x_{2}-s_{2}=6 \\
&x_{1}+2 x_{2}+s_{3}=3 \\
&x_{1}, x_{2}, s_{1}, s_{2}, s_{3} \geq 0
\end{aligned}
$$

حالات خاص مسئله برنامه ریزی خطی در تحقیق در عملیات 1
حالات خاص مسائل برنامه ریزی خطی عبارت هستند از:
- جواب بهینه چندگانه
- جواب تبهگن یا تباهیده
- منطقه موجه نامحدود
- جواب بهینه نامحدود
- جواب بهینه محدود
- عدم وجود جواب بهینه یا عدم وجود منطقه موجه
جواب بهینه چندگانه
«جواب بهینه چندگانه» (Multiple Optimal Solution)، حالت خاصی است که در آن، جواب بهینه بر روی بیش از یک نقطه منطبق میشود. به عبارت دیگر، در این حالت، برخلاف حالت کلی مسائل برنامه ریزی خطی، بیش از یک جواب بهینه وجود دارد. معمولا در صورت موازی بودن تابع هدف با یکی از محدودیتهای مسئله، احتمال رخ دادن جواب بهینه چندگانه افزایش مییابد.
در جدول سیمپلکس، اگر ضریب حداقل یکی از متغیرهای غیر اساسی در سطر ضرایب تابع هدف برابر صفر باشد، حالت جواب بهینه چندگانه در مسئله برنامه ریزی خطی به وجود میآید. به عنوان مثال، مسئله زیر را در نظر بگیرید:
$$
\begin{aligned}
\text { Max } &z=3 x_ { 1 } + 3 x_ { 2 }\\
\text { s.t. } &x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
مسئله بالا، در دو مختصات (2,1) و (0,3)، دارای جواب بهینه به مقدار 9 است. با حل مسئله بالا به روش سیمپلکس، جدول نهایی به شکل زیر خواهد بود.
| RHS | S3 | S2 | S1 | X2 | X1 | Z | |
| 3 | 0 | 0 | 1 | 1 | 1 | 0 | X2 |
| 6 | 0 | 1 | 1 | 0 | 3 | 0 | S2 |
| 4 | 1 | 0 | 0 | 0 | 1 | 0 | S3 |
| 9 | 0 | 0 | 3 | 0 | 0 | 1 | Z |
همانطور که مشاهده میکنید، ضریب یکی از متغیرهای غیر اساسی در جدول نهایی سیمپلکس برابر صفر است. این موضوع، وجود جواب بهینه چندگانه را نشان میدهد. به علاوه، اگر تابع هدف و محدودیت اول موازی هستند. با شناسایی این مسئله میتوانستیم احتمال رخ دادن جواب بهینه چندگانه را پیشبینی کنیم.
جواب تبهگن یا تباهیده
در حل مسائل برنامه ریزی خطی به روش ترسیمی، مشاهده کردیم که هر نقطه گوشه در منطقه موجه، از تقاطع معادله خط دو محدودیت تشکیل میشود. در صورت تشکیل یک نقطه گوشه از تقاطع بیش از دو معادله، «جواب تبهگن» (Degenerate Solution) رخ میدهد.
در روش ترسیمی میتوان این حالت خاص را به خوبی مشاهده کرد و تشخیص داد. وجود جواب تبهگن در یک مسئله، احتمال رخ دادن حلقه در روند حل را افزایش داده و سرعت حل به روش سیمپلکس را کاهش میدهد. البته این معنی نرسیدن به جواب بهسیه نیست.
صفر شدن مقدار یکی از متغیرهای اساسی در جدول سیمپلکس، نشاندهنده تبهگن بودن مسئله است. مسئله زیر را در نظر بگیرید:
$$
\begin{aligned}
\text { Max } &z=4 x_ { 1 } + 3 x_ { 2 }\\
\text { s.t. } &x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 2 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
در صورت حل مسئله بالا به روش سمپلکس، جدول سوم به شکل زیر در میآید.
| RHS | S3 | S2 | S1 | X2 | X1 | Z | |
| 1 | 0 | 1/3- | 2/3 | 1 | 0 | 0 | X2 |
| 2 | 0 | 1/3 | 1/3 | 0 | 1 | 0 | X1 |
| 0 | 1 | 1/3- | 1/3- | 0 | 0 | 0 | S3 |
| 11 | 0 | 1/3 | 10/3 | 0 | 0 | 1 | Z |
در این حالت، باید از بین دو متغیر S1 و S2، یکی را به عنوان متغیر ورودی انتخاب کرد. در صورت انتخاب متغیر S1، دوباره باید از بین متغیرهای X1 و X2، یکی را به عنوان متغیر خروجی انتخاب کرد.
در اغلب مسائل تبهگن، به جای وجود یک گزینه برای ورود و خروج در هر مرحله، مانند این مثال، چندین گزینه وجود خواهد داشت. به علاوه، همانطور که مشاهده میکنید، مقدار متغیر اساسی S3 برابر با صفر شده است. همین موضوع، تبهگن بودن مسئله را نمایش میدهد.
منطقه موجه نامحدود
در مسائل بیشینهسازی، اگر منطقه موجه توسط محدودهای مسئله بسته نشوند، حالت «منطقه موجه نامحدود» (unbounded Solution) رخ میدهد. در این حالت، جواب بهینه میتواند محدود یا نامحدود باشد.
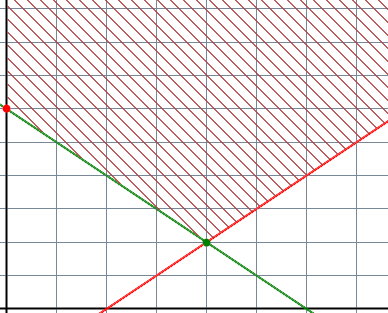
غیر مثبت بودن تمام ضرایب یک متغیر غیر اساسی، نشان دهنده نامحدود بودن منطقه موجه است. در صورت وجود ضریب منفی در سطر تابع هدف و عدم وجود عدد مثبت در ستون آن ضریب (عدم امکان انتخاب متغیر خروجی)، علاوه بر منطقه موجه، جواب بهینه نیز نامحدود میشود. مسئله زیر را در نظر بگیرید:
$$
\begin{aligned}
\text { Max } &z=4 x_ { 1 } + 3 x_ { 2 }\\
\text { s.t. } &x_ { 1 }+x_ { 2 } \geq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
با حل مسئله بالا به روش سیمپلکس، به جدول نهایی زیر میرسیم.
| RHS | M | S3 | S2 | S1 | X2 | X1 | Z | |
| 5 | 0 | 2 | 1- | 0 | 1 | 0 | 0 | X2 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | X1 |
| 6 | 1- | 3 | 1- | 1 | 0 | 0 | 0 | S1 |
| 31 | M | 10 | 3- | 0 | 0 | 0 | 1 | Z |
در جدول بالا، تمام ضرایب متغیر غیر اساسی S2، منفی یا صفر هستند. این موضوع، نشان دهنده وجود منطقه موجه نامحدود است. علاوه بر این، در سطر ضرایب تابع هدف، یک عدد منفی وجود دارد. به عبارت دیگر، مسئله هنوز به جواب بهینه نرسیده اما امکان ادامه دادن آن هم وجود ندارد.
عدم وجود منطقه موجه یا عدم وجود جواب بهینه موجه
«عدم وجود منطقه موجه» (Infeasible Solution)، زمانی رخ میدهد که هیچ راهحلی برای پاسخ به مسئله برنامهریزی وجود نداشته باشد. به عبارت دیگر، در این حالت نمیتوان منطقه مشترکی بین تمام محدودیتهای مسئله پیدا کرد. تصویر زیر، حالت عدم وجود جواب بهینه را نمایش میدهد. همان طور که مشاهده میکنید، هیچ منطقهای برای پیدا کردن جواب وجود ندارد.
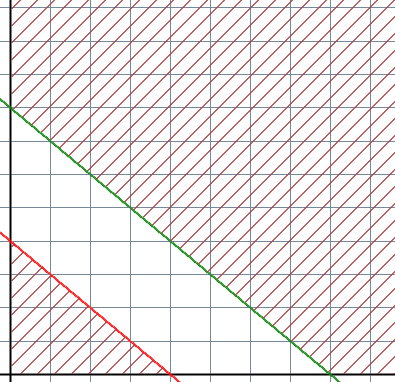
به طور کلی، خطا در فرموله کردن مسئله، تعریف نادرست مسئله یا خطا در وارد کردن اطلاعات میتواند منجر به عدم وجود جواب بهینه موجه شود. در حل مسئله برنامه ریزی خطی به روش سیمپلکس، اگر در جدول نهایی، یک یا چند متغیر مصنوعی با مقدار غیر صفر وجود داشته باشد، حالت عدم وجود منطقه موجه رخ میدهد. به عنوان مثال، مسئله زیر را در نظر بگیرید:
$$
\begin{aligned}
\text { Max } &z=4 x_ { 1 } + 3 x_ { 2 }\\
\text { s.t. } &x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \geq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
پس از حل مسئله بالا به روش سیمپلکس، به جدول نهایی زیر میرسیم.
| RHS | R1 | S3 | S2 | S1 | X2 | X1 | Z | |
| 1 | 0 | 0 | 1/3- | 2/3 | 1 | 0 | 0 | X2 |
| 2 | 0 | 0 | 1/3 | 1/3 | 0 | 1 | 0 | X1 |
| 2 | 1 | 1- | 1/3- | 1/3- | 0 | 0 | 0 | R1 |
| 2M+11- | 0 | M | M/3+1/3 | M/3+10/3 | 0 | 0 | 1 | Z |
در جدول بالا، متغیر مصنوعی دارای مقدار غیر صفر است. این موضوع، عدم وجود منطقه موجه و جواب بهینه را نمایش میدهد.
مسئله ثانویه در تحقیق در عملیات 1
هر مسئله برنامه ریزی خطی را میتوان به دو صورت (مسئله اولیه و مسئله ثانویه) نوشت. از نظر تعداد متغیرهای تصمیم و محدودیتها، مسئله ثانویه، عکس مسئله اولیه است. تعداد متغیرهای هر یک، برابر تعداد متغیرهای تصمیم دیگری بوده و اعداد سمت راست هر یک، برابر ضریب متغیرهای تصمیم در تابع هدف دیگری است. به عنوان مثال، مسئله زیر را در نظر بگیرید:
$$
\begin{aligned}
\text { Max } &z=4 x_ { 1 } + 3 x_ { 2 }\\
\text { s.t. } &x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
اگر مسئله بالا را به سیمپلکس ثانویه تبدیل کنیم، فرم آن به شکل زیر در میآید:
$$
\begin{aligned}
\text { Min } &Y= 3 y_ { 1 } + 3 y_ { 2 } + 4 y_ { 3 }\\
\text { s.t. } & y_ { 1 } + 2 y_ { 2 } + y_ { 3 } \geq 4 \\
& y_ { 1 } - y_ { 2 } \geq 3 \\
&y_ { 1 } \geq 0, \space y_ { 2 } \geq 0,\space y_ { 3 } \geq 0
\end{aligned}
$$
اکنون میتوانیم مسئله بالا را به روش سیمپلکس حل کنیم. جواب بهینه در این مسئله با مسئله اولیه هیچ تفاوتی نخواهد داشت. البته تعداد مراحل و میزان محاسبات در اغلب موارد متفاوت هستند. سیمپلکس ، برای حل مسائل برنامه ریزی خطی با تعداد محدودیتهای زیاد (بیشتر از متغیرهای تصمیم)، کاربرد بسیار خوبی دارد.
مراحل تبدیل کردن مسئله اولیه به ثانویه
در بخش قبلی، یک مثال از مسئله اولیه و ثانویه را نمایش دادیم. در این بخش، مراحل تبدیل مسئله اولیه به ثانویه بر اساس همان مثال توضیح میدهیم.
مطابقت دادن نامساویها با نوع تابع هدف
در مسائل بیشینهسازی، تمام نامساویها باید به صورت کوچکتر مساوی (≥) بوده و در مسائل کمینهسازی، تمام نامساویها باید به صورت بزرگتر مساوی (≤) باشند. در مسئله زیر، تمام نامساویها با تابع هدف مطابقت دارند.
$$
\begin{aligned}
\text { Max } &z=4 x_ { 1 } + 3 x_ { 2 }\\
\text { s.t. } &x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
تبدیل نوع بهینهسازی
مسائل بیشینهسازی (Max) باید به کمینهسازی (Min) و مسائل کمینهسازی باید به بیشینهسازی تبدیل شوند. به این ترتیب، نوشتن مسئله ثانویه را از تعیین نوع بهینهسازی آن شروع میکنیم:
$$
\begin{aligned}
\text { Min } &Y
\end{aligned}
$$
در مسئله ثانویه، برای نمایش تابع هدف، به جای حرف Z از حرف Y استفاده میشود.
تعریف متغیرهای تصمیم
به ازای هر محدودیت در مسئله اولیه، باید یک متغیر تصمیم در مسئله ثانویه در نظر گرفته شود. مسئله مورد بررسی ما، سه محدودیت دارد.
$$
\begin{aligned}
&x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
بنابراین، سه متغیر را با عنوانهای y2 ،y1 و y3 به عنوان متغیرهای تصمیم مسئله دوگان تعریف میکنیم.

تعیین ضرایب متغیرهای تصمیم در تابع هدف
در مرحله بعدی، عدد سمت راست نامساویها به عنوان ضریب متغیرهای تصمیم در نظر گرفته میشوند. به این ترتیب، میتوان تابع هدف مسئله ثانویه را نوشت.
$$
\begin{aligned}
&x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
&x_ { 1 } \geq 0, x_ { 2 } \geq 0
\end{aligned}
$$
اعداد سمت راست نامساویهای بالا برابر 3، 3 و 4 هستند. این اعداد را به ترتیب به متغیرهای y2 ،y1 و y3 اختصاص مییابند. بنابراین، تابع هدف مسئله ثانویه به شکل زیر در میآید:
$$
\begin{aligned}
\text { Min } &Y= 3 y_ { 1 } + 3 y_ { 2 } + 4 y_ { 3 }\\
\end{aligned}
$$
تعیین اعداد سمت راست نامساویها
ضرایب تابع هدف مسئله اولیه، اعداد سمت راست نامساویها در مسئله ثانویه خواهند بود.
$$
\begin{aligned}
\text { Max } &z=4 x_ { 1 } + 3 x_ { 2 }\\
\end{aligned}
$$
در مثال مورد بررسی، این اعداد برابر 4 و 3 هستند. به این ترتیب، در مسئله ثانویه، این اعداد به صورت زیر نوشته میشوند:
$$
\begin{aligned}
\text { Min } &Y= 3 y_ { 1 } + 3 y_ { 2 } + 4 y_ { 3 }\\
\\ s.t. & & \geq 4
\\ & & \geq 3
\end{aligned}
$$
تعیین ضرایب محدودیتهای جدید
به منظور تعیین ضرایب متغیرها در هر محدودیت مسئله ثانویه، از ضرایب متغیرهای تصمیم در محدودیتهای مسئله اولیه استفاده میشود. به عنوان مثال، ضرایب متغیر تصمیم x1 در مسئله اولیه، به ترتیب برابر 1، 2 و 1 هستند:
$$
\begin{aligned}
\text { s.t. } &x_ { 1 }+x_ { 2 } \leq 3 \\
& 2 x_ { 1 } - x_ { 2 } \leq 3 \\
& x_ { 1 } \leq 4 \\
\end{aligned}
$$
ضرایب متغیر تصمیم x1، به عنوان ضرایب y2 ،y1 و y3 در محدودیت اول مسئله ثانویه در نظر گرفته میشوند:
$$
\begin{aligned}
\text { Min } &Y= 3 y_ { 1 } + 3 y_ { 2 } + 4 y_ { 3 }\
\\ s.t. \space & y_ { 1 } + 2 y_ { 2 } + y_ { 3 } \geq 4
\end{aligned}
$$
دقت کنید که به دلیل کمینهسازی بودن مسئله ثانویه، نامساوی محدودیت آن، به صورت بزرگتر مساوی است. به همین شکل، ضرایب متغیر تصمیم x1 در محدودیتهای مسئله اولیه (اعداد 1، 1- . 0) را به عنوان ضرایب محدودیت دوم مسئله ثانویه در نظر میگیریم.
$$
\begin{aligned}
\text { Min } &Y= 3 y_ { 1 } + 3 y_ { 2 } + 4 y_ { 3 }\
\\ s.t. \space & y_ { 1 } + 2 y_ { 2 } + y_ { 3 } \geq 4
\\& y_ { 1 } - y_ { 2 } \geq 3
\end{aligned}
$$
نوشتن محدودیت غیر منفی بودن متغیرها
در انتها، محدودیت غیر منفی بودن متغیرهای تصمیم را به تابع هدف و دیگر نامساویها اضافه میکنیم. فرم نهایی مسئله ثانویه به شکل زیر در میآید:
$$
\begin{aligned}
\text { Min } &Y= 3 y_ { 1 } + 3 y_ { 2 } + 4 y_ { 3 }\\
\text { s.t. } & y_ { 1 } + 2 y_ { 2 } + y_ { 3 } \geq 4 \\
& y_ { 1 } - y_ { 2 } \geq 3 \\
&y_ { 1 } \geq 0, \space y_ { 2 } \geq 0,\space y_ { 3 } \geq 0
\end{aligned}
$$
همانٰطور که اشاره کردیم، اصول حل مسئله اولیه و ثانویه تفاوتی با هم ندارند.
حالت های خاص مسئله ثانویه
در نوشتن مسئله ثانویه، امکان رخ دادن دو حالت خاص وجود دارد. در ادامه به توضیح این دو حالت و نحوه تبدیل آنها میپردازیم.
وجود محدودیت مساوی در مسئله اولیه
در صورت وجود محدودیتهای مساوی در مسئله اولیه، متغیر تصمیم مربوط به آن، به عنوان یک متغیر آزاد در علامت در نظر گرفته میشود. به عنوان مثال، اگر محدودیت اول یک مسئله اولیه با سه محدودیت، از نوع مساوی بود، باید محدودیتهای نهایی مسئله ثانویه را به صورت زیر نوشت:
y1 آزاد در علامت
0 ≤ y2 و y3
وجود متغیر آزاد در علامت در مسئله اولیه
در صورت وجود متغیر آزاد در مسئله اولیه، محدودیت مربوط به آن، به صورت مساوی نوشته میشود. به عنوان مثال، اگر متغیر x2 در مسئله اولیه، آزاد در علامت باشد، محدودیت دوم در مسئله ثانویه یک معادله خواهد بود.

حالت های حل مسئله برنامه ریزی خطی به روش سیمپلکس
تفاوت اصلی در روش مورد استفاده برای حل مسائل مختلف برنامهریزی خطی، نوع نامساویهای آنها است. در بخشهای قبلی، یک مسئله برنامهریزی خطی با محدودیتهای کوچکتر مساوی را حل کردیم. برای مسائل دارای محدودیتهای مساوی یا بزرگتر مساوی، شرایط متفاوت است.در هر حالت، حل مسئله با نوشتن فرم استاندارد شروع میشود.
هنگام نوشتن فرم استاندارد یک مسئله با محدودیتهای بزرگتر مساوی یا مساوی، به دلیل کم کردن متغیر مازاد از محدودیتها، مبدا مختصات به خارج منطقه موجه انتقال مییابد. از اینرو، به یک متغیر دیگر برای بازگرداندن مبدا مختصات به منطقه موجه نیاز داریم. به این متغیر، متغیر مصنوعی میگویند. در درس تحقیق در عملیات 1 معمولا دو با عنوانهای روش M بزرگ و روش دو مرحلهای، برای حل مسائل با محدودیتهای بزرگتر مساوی یا مساوی آموزش داده میشوند.
حل مسئله برنامه ریزی خطی به روش M بزرگ
در روش M بزرگ، عددی بسیار بزرگ (M) در قالب ضریب متغیرهای مصنوعی به سمت راست تابع هدف اضافه (مسائل کمینهسازی) یا کم (مسائل بیشینهسازی) میشود. این کار، امکان بازگشت منطقه موجه به حالت اصلی و شروع حل مسئله به روش سیمپلکس را فراهم میکند. برای آشنایی بهتر با روش M بزرگ، مسئله زیر را در نظر بگیرید:
$$
\begin{array}{ll}
\operatorname{Min} Z= & 2 x_{1}+x_{2} \\
\text { st. } \quad & 3 x_{1}+x_{2} \geq 3 \\
& 4 x_{1}+3 x_{2} \geq 6 \\
& x_{1}+2 x_{2} \leq 3 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
فرم استاندارد مسئله بالا به شکل زیر نوشته میشود:
$$
\begin{aligned}
{Max}& -Z+2 x_{1}+x_{2}=0 \\
\text { s.t. } & 3 x_{1}+x_{2}-s_{1}=3 \\
&4 x_{1}+3 x_{2}-s_{2}=6 \\
&x_{1}+2 x_{2}+s_{3}=3 \\
&x_{1}, x_{2}, s_{1}, s_{2}, s_{3} \geq 0
\end{aligned}
$$
در این مسئله، دو محدودیت بزرگتر یا مساوی وجود دارد. برای حل مسئله، باید دو متغیر مصنوعی به سمت چپ این محدودیتها اضافه کنیم. این متغیرها را با R1 و R2 نمایش میدهیم:
$$
\begin{array}{ll}
\operatorname{Max}- & Z+2 x_{1}+x_{2}=0 \\
& 3 x_{1}+x_{2}-s_{1}+R_{1}=3 \\
& 4 x_{1}+3 x_{2}-s_{2}+R_{2}=6 \\
& x_{1}+2 x_{2}+s_{3}=3 \\
& x_{1}, x_{2}, s_{1}, s_{2}, s_{3}, R_{1}, R_{2} \geq 0
\end{array}
$$
در روش M بزرگ، هر یک از متغیرهای مصنوعی را در عدد M ضرب کرده به به سمت چپ تابع هدف اضافه میکنیم. به این ترتیب، مسئله برای حل به روش M بزرگ آماده میشود:
$$
\begin{array}{ll}
\operatorname{Max}- & Z+2 x_{1}+x_{2}+M \cdot R_{1}+M \cdot R_{2}=0 \\
& 3 x_{1}+x_{2}-s_{1}+R_{1}=3 \\
& 4 x_{1}+3 x_{2}-s_{2}+R_{2}=6 \\
& x_{1}+2 x_{2}+s_{3}=3 \\
& x_{1}, x_{2}, s_{1}, s_{2}, s_{3}, R_{1}, R_{2} \geq 0
\end{array}
$$
جدول اولیه سیمپلکس برای مسئله بالا، به شکل زیر است.
| RHS | R2 | R1 | s3 | s2 | s1 | x2 | x1 | Z | |
| 3 | 0 | 1 | 0 | 0 | 1- | 1 | 3 | 0 | R1 |
| 6 | 1 | 0 | 0 | 1- | 0 | 3 | 4 | 0 | R2 |
| 3 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | s3 |
| 0 | M | M | 0 | 0 | 0 | 1 | 2 | 1- | Z |
جدول بالا، علاوه بر وجود متغیرهای مصنوعی، یک تفاوت بزرگ با مسائل دارای محدودیتهای کوچکتر مساوی دارد. برای شروع حل جدول سیمپلکس، بردار ستونی متغیرهای اساسی (متغیرهای ستون سمت چپ جدول) باید یکه باشد. در جدول زیر، ستونهای مربوط به متغیرهای اساسی را از جدول بالا جدا کردهایم.
| R2 | R1 | s3 | |
| 0 | 1 | 0 | R1 |
| 1 | 0 | 0 | R2 |
| 0 | 0 | 1 | s3 |
| M | M | 0 | Z |
همانطور که مشاهده میکنید، بردارهای ستونی یکه R1 و R2 نیستند. بنابراین، باید این ستونها را یکه کنیم. مراحل یکه کردن این ستونها مشابه مراحل توضیح داده شده در مثال سیمپلکس معمولی است. با انجام این مراحل، جدول زیر تشکیل میشود.
| RHS | R2 | R1 | s3 | s2 | s1 | x2 | x1 | Z | |
| 3 | 0 | 1 | 0 | 0 | 1- | 1 | 3 | 0 | R1 |
| 6 | 1 | 0 | 0 | 1- | 0 | 3 | 4 | 0 | R2 |
| 3 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | s3 |
| 9M- | 0 | 0 | 0 | M | M | 4M+1- | 7M+2- | 1- | Z |
با یکه شدن بردارهای ستونی متغیرهای اساسی، میتوانیم جدول سیمپلکس را مانند حالت معمولی حل کنیم. به عنوان مثال، در مرحله اول، باید متغیر x1 را به عنوان متغیر ورودی در نظر گرفت؛ چراکه ضریب آن در تابع هدف، منفیترین مقدار را دارد (7M+2-). با حل جدول بالا و به روزرسانی آن طی چند مرحله، به جدول نهایی زیر میرسیم.
| RHS | R2 | R1 | s3 | s2 | s1 | x2 | x1 | Z | |
| 3/5 | 1/5- | 3/5 | 0 | 1/5 | 3/5- | 0 | 1 | 0 | x1 |
| 6/5 | 3/5 | 4/5- | 0 | 3/5- | 4/5 | 1 | 0 | 0 | x2 |
| 0 | 1- | 1 | 1 | 1 | 1- | 0 | 0 | 0 | s3 |
| 12/5- | M-1/5 | M-2/5 | 0 | 1/5 | 2/5 | 0 | 0 | 1- | Z |
مطابق با جدول نهایی سیمپلکس، مقدار متغیرهای تصمیم و جواب بهینه به دست میآید.
حل مسئله برنامه ریزی خطی به روش دو مرحله ای
دو مرحله حل مسئله برنامهریزی خطی به روش دو مرحلهای عبارت هستند از:
- نوشتن تابع هدف مصنوعی و تعیین جواب موجه اولیه
- پیدا کردن جواب بهینه از روی تابع اصلی
مدل ریاضی نوشته در بخش قبلی را در نظر بگیرید:
$$
\begin{array}{ll}
\operatorname{Max}- & Z+2 x_{1}+x_{2}=0 \\
& 3 x_{1}+x_{2}-s_{1}+R_{1}=3 \\
& 4 x_{1}+3 x_{2}-s_{2}+R_{2}=6 \\
& x_{1}+2 x_{2}+s_{3}=3 \\
& x_{1}, x_{2}, s_{1}, s_{2}, s_{3}, R_{1}, R_{2} \geq 0
\end{array}
$$
در این مدل، به جای تابع هدف اصلی، یک تابع هدف مصنوعی مینویسیم:
$$
\begin{array}{ll}
\operatorname{Min} & W=R_{1} + R_{2} \\
& 3 x_{1}+x_{2}-s_{1}+R_{1}=3 \\
& 4 x_{1}+3 x_{2}-s_{2}+R_{2}=6 \\
& x_{1}+2 x_{2}+s_{3}=3 \\
& x_{1}, x_{2}, s_{1}, s_{2}, s_{3}, R_{1}, R_{2} \geq 0
\end{array}
$$
جدول اولیه سیمپلکس برای مدل بالا به صورت زیر خواهد بود.
| RHS | R2 | R1 | s3 | s2 | s1 | x2 | x1 | W | |
| 3 | 0 | 1 | 0 | 0 | 1- | 1 | 3 | 0 | R1 |
| 6 | 1 | 0 | 0 | 1- | 0 | 3 | 4 | 0 | R2 |
| 3 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | s3 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1- | W |
در این روش نیز مانند روش M بزرگ، ابتدا باید بردارهای ستونی متغیرهای اساسی را یکه کرد. پس از این کار، جدول زیر ایجاد میشود.
| RHS | R2 | R1 | s3 | s2 | s1 | x2 | x1 | W | |
| 3 | 0 | 1 | 0 | 0 | 1- | 1 | 3 | 0 | R1 |
| 6 | 1 | 0 | 0 | 1- | 0 | 3 | 4 | 0 | R2 |
| 3 | 0 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | s3 |
| 9- | 0 | 0 | 0 | 1 | 1 | 4- | 7- | 1- | W |
اکنون جدول سیمپلکس آماده مرحله اول محاسبات است. پس از انجام محاسبات مانند مثالهای قبلی، جدول نهایی مرحله اول به شکل زیر در میآید.
| RHS | R2 | R1 | s3 | s2 | s1 | x2 | x1 | W | |
| 3/5 | 1/5- | 3/5 | 0 | 1/5 | 3/5- | 0 | 1 | 0 | x1 |
| 6/5 | 3/5 | 4/5- | 0 | 3/5- | 4/5 | 1 | 0 | 0 | x2 |
| 0 | 1- | 1 | 1 | 1 | 1- | 0 | 0 | 0 | s3 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1- | W |
در مرحله دو از حل مسئله، تمام سطرهای جدول بالا را دوباره مینویسیم اما ستونهای متغیرهای مصنوعی را حذف کرده و به جای سطر مربوط به تابع هدف مصنوعی، اطلاعات تابع هدف اصلی را وارد میکنیم.
| RHS | s3 | s2 | s1 | x2 | x1 | Z | |
| 3/5 | 0 | 1/5 | 3/5- | 0 | 1 | 0 | x1 |
| 6/5 | 0 | 3/5- | 4/5 | 1 | 0 | 0 | x2 |
| 0 | 1 | 1 | 1- | 0 | 0 | 0 | s3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1- | Z |
بردارهای ستونی جدول سیمپلکس بالا، یکه نیستند. با یکه کردن این ستونها، به جواب بهینه میرسیم.
| RHS | s3 | s2 | s1 | x2 | x1 | Z | |
| 3/5 | 0 | 1/5 | 3/5- | 0 | 1 | 0 | x1 |
| 6/5 | 0 | 3/5- | 4/5 | 1 | 0 | 0 | x2 |
| 0 | 1 | 1 | 1- | 0 | 0 | 0 | s3 |
| 12/5- | 0 | 1/5 | 2/5 | 0 | 0 | 1- | Z |

روش دوال سیمپلکس در تحقیق در عملیات 1
در بخش قبلی مشاهده کردیم که در صورت وجود محدودیتهای مساوی یا بزرگتر مساوی در مسئله برنامه ریزی خطی، حل آن به روش سیمپلکس نیازمند تعریف متغیرهای مصنوعی خواهد بود. «سیمپلکس دوگان» (Dual Simplex)، روشی مشابه روش سیمپلکس است که به منظور حل مسائل برنامهریزی خطی، بدون نیاز به متغیرهای مصنوعی، مورد استفاده قرار میگیرد. مراحل اجرای این روش عبارت هستند از:
- نوشتن فرم استاندارد مسئله
- تشکیل جدول سیمپلکس
- انتخاب متغیر خروجی با شناسایی منفیترین عدد سمت راست
- انتخاب متغیر ورودی با تقسیم اعداد سطر تابع هدف بر اعداد سطر کلیدی
- یکه کردن بردار ستونی متغیر اساسی ورودی
- بررسی شرط بهینگی
در روش دوال سیمپلکس، نحوه نوشتن فرم استاندارد، انتخاب متغیر خروجی، انتخاب متغیر ورودی و بررسی شرط بهینگی با روش سیمپلکس معمولی تفاوت دارد. این تفاوتها را با یک مثال مورد بررسی قرار میدهیم.
حل مسئله دوال سیمپلکس
مسئله زیر را در نظر بگیرید:
$$
\begin{array}{ll}
\operatorname{Min} Z= & 2 x_{1}+x_{2} \\
\text { st. } \quad & 3 x_{1}+x_{2} \geq 3 \\
& 4 x_{1}+3 x_{2} \geq 6 \\
& x_{1}+2 x_{2} \leq 3 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
این مسئله را در بخشهای قبلی به فرم استاندارد سیمپلکس اولیه تبدیل کردیم. برای تبدیل مسئله بالا به فرم استاندارد سیمپلکس ثانویه، ابتدا باید مسئله را به صورت بیشینهسازی بنویسیم و تمام نامساویها را به کوچکتر مساوی تغییر دهیم:
$$
\begin{array}{ll}
\operatorname{Max} -Z = &-2 x_{1}-x_{2} \\
\text { st. } \quad & -3 x_{1}-x_{2} \leq -3 \\
& -4 x_{1}-3 x_{2} \leq -6 \\
& x_{1}+2 x_{2} \leq 3 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
با ضریب تابع هدف در عدد (1-)، مسئله از کمینهسازی (Min) به بیشینهسازی (Max) تبدیل میشود. ضرب محدودیتهای اول و دوم در عدد (1-) نیز، علامت نامساوی آنها را از بزرگتر مساوی به کوچکتر مساوی تبدیل میکند. اکنون باید با بردن عبارتهای سمت راست تابع هدف به سمت چپ تابع و اضافه کردن متغیرهای کمکی به نامساویها، فرم استاندارد مسئله برای حل به روش سیمپلکس ثانویه را بنویسیم:
$$
\begin{array}{ll}
\operatorname{Max} &-Z + 2 x_{1} +x_{2} \\
\text { st. } \quad & -3 x_{1}-x_{2} + s_1 = -3 \\
& -4 x_{1}-3 x_{2} + s_2 = -6 \\
& x_{1}+2 x_{2} + s_3 =3 \\
& x_{1}, x_{2} \geq 0
\end{array}
$$
برای شروع حل مسئله بالا، جدول اولیه سیمپلکس آن را ایجاد میکنیم.
| RHS | s3 | s2 | s1 | x2 | x1 | Z | |
| 3- | 0 | 0 | 1 | 1- | 3- | 0 | s1 |
| 6- | 0 | 1 | 0 | 3- | 4- | 0 | s2 |
| 3 | 1 | 0 | 0 | 2 | 1 | 0 | s3 |
| 0 | 0 | 0 | 0 | 1 | 2 | 1- | Z |
در روش دوال سیمپلکس، به منظور تعیین متغیر خروجی، ابتدا اعداد سمت راست (RHS) را مورد بررسی قرار میدهیم. هر عددی که منفیتر بود، متغیر سطر مربوط به آن، گزینه اصلی برای خروج از ستون متغیرهای اساسی (ستون سمت چپ) است. در جدول بالا، عدد (6-)، کوچکترین عدد سمت راست است. بنابراین، سطر مربوط به آن، سطر کلیدی و متغیر s2، متغیر خروجی از متغیرهای اساسی خواهد بود.
در قدم بعدی باید متغیر ورودی انتخاب شود. این کار، با تقسیم اعداد سطر تابع هدف (Z) بر اعداد منفی سطر کلیدی انجام میگیرد. ستون مربوط به هر تقسیمی که نتیجه آن از نظر قدر مطلق کوچکترین بود، ستون کلیدی است. در جدول بالا، حاصل تقسیم عدد 1 بر (3-) نسبت به حاصل تقسیم عدد 2 بر (4-) از نظر قدر مطلق کوچکتر است. در نتیجه، x2 به عنوان متغیر ورودی و ستون مربوط به آن به عنوان ستون کلیدی در نظر گرفته میشود. یکه کردن ستون کلیدی با روش سیمپلکس معمولی تفاوتی ندارد. پس از انجام این فرآیند، جدول زیر به وجود میآید.
| RHS | s3 | s2 | s1 | x2 | x1 | Z | |
| 1- | 0 | 1/3- | 1 | 0 | 5/3- | 0 | s1 |
| 2 | 0 | 1/3- | 0 | 1 | 4/3 | 0 | x2 |
| 1- | 1 | 2/3 | 0 | 0 | 5/3- | 0 | s3 |
| 2- | 0 | 1/3 | 0 | 0 | 2/3 | 1- | Z |
شرط بهینگی در حل مسئله برنامهریزی خطی به روش دوال سیمپلکس، منفی نبودن اعداد سمت راست (به غیر سطر تابع هدف) است. بر اساس این شرط، جدول بالا، جواب بهینه را نمایش نمیدهد. به همین دلیل، باید مراحل قبلی را ارضا شدن ضرط بهینگی ادامه دهیم. جدول نهایی سیمپلکس برای این مسئله به صورت زیر خواهد بود.
| RHS | s3 | s2 | s1 | x2 | x1 | Z | |
| 3/5 | 0 | 1/5 | 3/5- | 0 | 1 | 0 | x1 |
| 6/5 | 0 | 3/5- | 4/5 | 1 | 0 | 0 | x2 |
| 0 | 1 | 1 | 1- | 0 | 0 | 0 | s3 |
| 12/5- | 0 | 1/5 | 2/5 | 0 | 0 | 1- | Z |
در جدول نهایی، مقادیر متغیرهای تصمیم برای رسیدن به جواب بهینه، قابل مشاهده هستند. به طور کلی، اگر تعداد محدودیتها نسبت به تعداد متغیرهای تصمیم مسئله بیشتر باشد، سرعت حل روش دوال سیمپلکس نسبت به روش سیمپلکس معمولی بالاتر خواهد بود.
مسئله حمل و نقل در تحقیق در عملیات 1
مسئله حمل و نقل، یکی از حالتهای خاص مسائل برنامه ریزی خطی در نظر گرفته میشود. هدف اصلی این مسئله، به حداقل رساندن (کمینهسازی) هزینه جابجایی از یک یا چند مبدا (محل عرضه) به یک یا چند مقصد (محل تقاضا) است.
مسائل حمل و نقل به دو نوع متوازن و نامتوازن تقسیم میشود:
- مسئله حمل و نقل متوازن: عرضه و تقاضا با هم برابر هستند.
- مسئله حمل و نقل نامتوازن: عرضه و تقاضا با هم برابر نیستند.
جدول زیر، نمونهای از یک مسئله حمل و نقل از مبداهای II ،I و III به مقصدهای B ،A و C را به همراه هزینه هر مسیر، عرضه مبدا و تقاضای مقصد نمایش میدهد.
| A | B | C | عرضه | |
| I | 2 | 7 | 5 | 200 |
| II | 3 | 4 | 2 | 300 |
| III | 5 | 4 | 7 | 500 |
| تقاضا | 200 | 400 | 400 | 1000 |
اگر اعداد مقابل ردیف تقاضا را با هم و اعداد مقابل ستون عرضه را با هم جمع کنیم، به عدد 1000 میرسیم. به دلیل برابر بودن این مقدار برای عرضه و تقاضا، مسئله حمل و نقل از نوع متوازن است. توجه داشته باشید که برای حل تمام مسائل حمل و نقل، عرضه و تقاضا باید برابر باشند. در صورت عدم برابری عرضه و تقاضا (نامتوازن بودن)، حل مسئله با اضافه کردن یک سطر یا ستون مجازی و اضافه کردن اختلاف بین عرضه و تقاضا صورت میگیرد.
همیشه حل مسائل حمل و نقل را با بررسی متوازن یا نامتوازن بودن عرضه و تقاضا شروع کنید. مسائل حمل و نقل نیز مانند دیگر مسائل برنامه ریزی خطی، با پیدا کردن جوابهای موجه اولیه و بررسی شرط بهینگی حل میشوند. روشهای مختلفی برای پیدا کردن جواب موجه اولیه وجود دارد. از متداولترین این روشها میتوان به موارد زیر اشاره کرد:
- روش گوشه شمال غربی
- روش کمترین هزینه
- روش تقریبی وگل
مراحل روش گوشه شمال غربی
روش گوشه شمال غربی، یکی از سادهترین روشها برای پیدا کردن جواب موجه اولیه در مسائل حمل نقل است. این روش طی مراحل زیر انجام میشود:
- بررسی متوازن بودن عرضه و تقاضا (متوازن کردن در صورت برابر نبودن عرضه و تقاضا)
- انتخاب گوشه شمال غربی مسئله (خانه بالا-چپ)
- بررسی عرضه و تقاضای مقابل خانه انتخابی و اختصاص کمترین عدد به آن (نوشتن عدد عرضه یا تقاضا درون خانه)
- کم کردن عدد اختصاص یافته از عرضه و تقاضای مقابل خانه انتخابی (یکی از اعداد عرضه یا تقاضا صفر خواهد شد.)
- حذف خانههای مقابل عرضه یا تقاضای صفر شده
- انتخاب گوشه شمال غربی از بین خانههای باقی مانده
- تکرار مراحل بالا تا اختصاص تمام مقادیر عرضه و تقاضا (صفر شدن تمام مقادیر)
- ضرب اعداد اختصاص یافته به خانهها در هزینه آنها و جمع حاصلضربها
حل مثال حمل و نقل به روش گوشه شمال غربی
در این بخش، به منظور درک بهتر مراحل پیدا کردن جواب موجه اولیه، به حل یک مثال میپردازیم. ماتریس زیر را در نظر بگیرید.
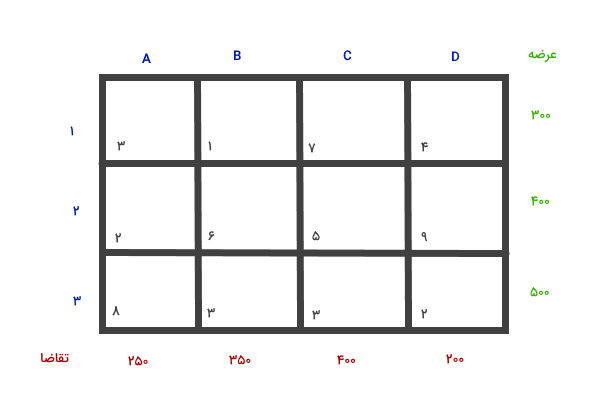
برای شروع، ابتدا متوازن بودن عرضه و تقاضا را بررسی میکنیم. به این منظور، مقادیر ستون عرضه را باهم و مقادیر سطر تقاضا را با هم جمع میبندیم و انتهای آنها مینویسیم.
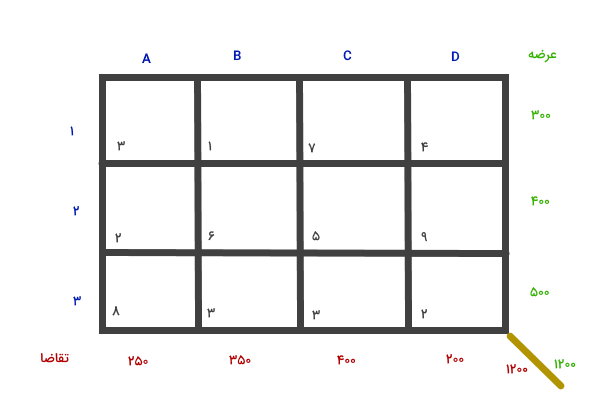
جمع عرضه و جمع تقاضا برابر 1200 است. بنابراین، این مسئله به عنوان یک مسئله متوازن در نظر گرفته میشود. در مرحله بعدی گوشه شمال غربی (خانه A1) را انتخاب میکنیم. مقدار تقاضای انتهای ستون این خانه برابر 250 و مقدار عرضه انتهای سطر این خانه برابر 300 است. از اینرو، عدد 250 را به خانه A1 اختصاص میدهیم و این عدد را از عرضه و تقاضا کم میکنیم.
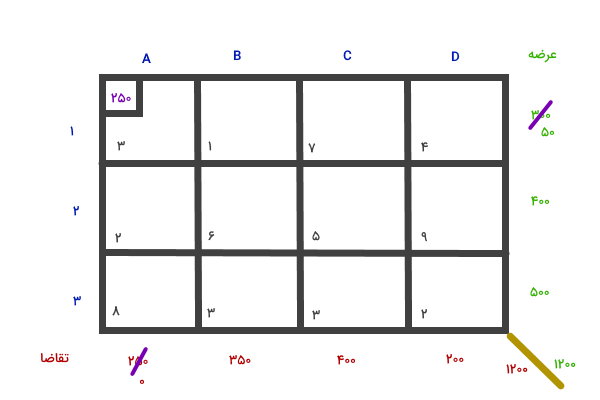
با انجام مراحل بالا، مقدار تقاضای ستون A برابر 0 میشود. به عبارت دیگر، هیچ تقاضایی برای اختصاص به خانههای دیگر این ستون باقی نمیماند. از اینرو، خانههای دیگر را خط میزنیم (حذف میکنیم) و به سراغ گوشه شمال غربی بعدی، یعنی خانه B1 میرویم.
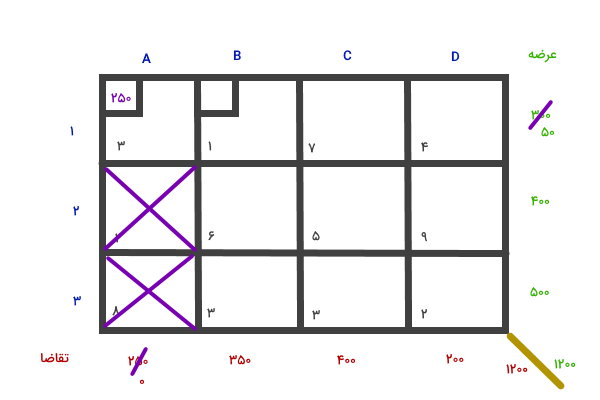
در سطر خانه B1، به اندازه 50 واحد عرضه و در ستون آن، به اندازه 350 واحد تقاضا وجود دارد. مقدار کمتر (50) را به این خانه اختصاص میدهیم. سپس، عدد اختصاص یافته را از سطر و ستون کم میکنیم.
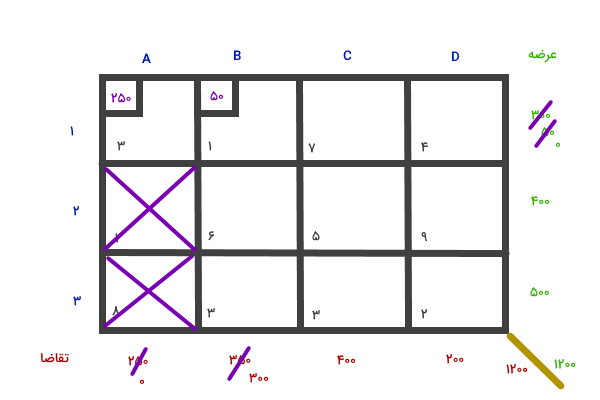
با این کار، عرضه سطر 1 به صفر میرسد. بنابراین باید خانههای باقیمانده در این سطر را حذف کنیم و به سراغ گوشه شمال غربی بعدی (خانه B2) برویم. از بین عرضه و تقاضای قابل تخصیص به این گوشه، تقاضا (عدد 300)، مقدار کمتری دارد. این عدد را به خانه B2 اختصاص میدهیم.
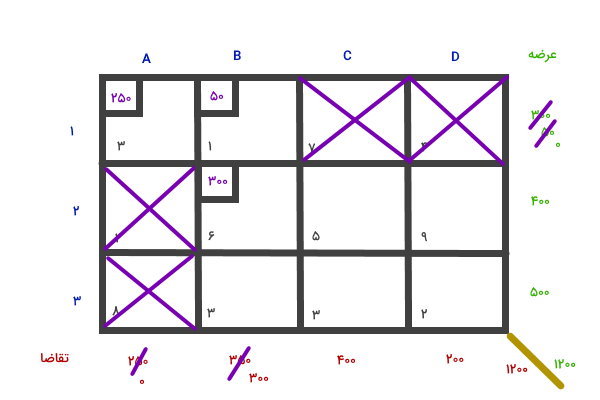
مقدار تخصیص یافته را از عرضه و تقاضا کم کرده و خانههای اضافی را حذف میکنیم. سپس، به سراغ گوشه شمال غربی بعدی (خانه C2) میرویم.
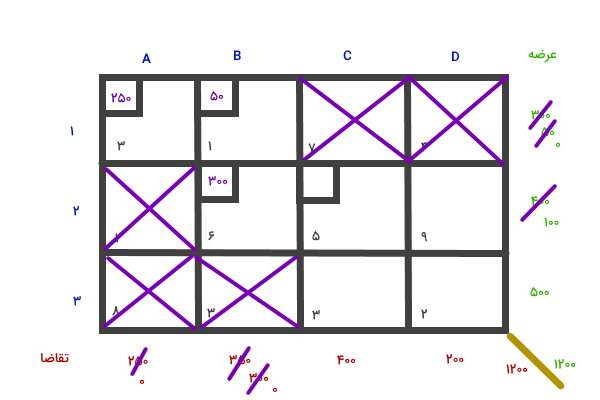
مراحل قبلی را برای خانه C2 تکرار میکنیم.
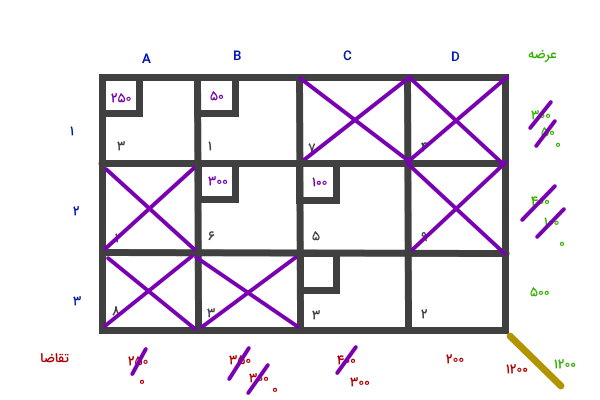
سپس، به سراغ خانه C3 میرویم.
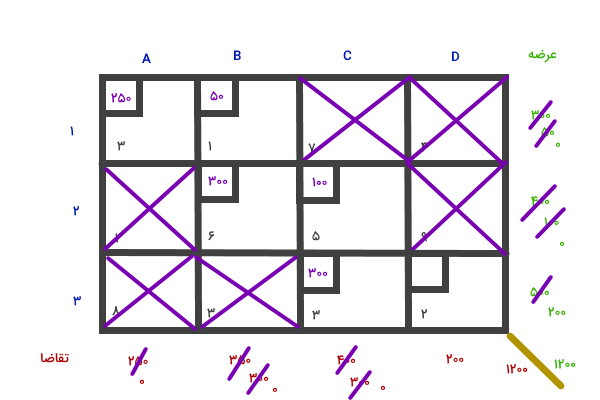
با تخصیص مقادیر باقیمانده به خانه D3، فرآیند تخصیص عرضه و تقاضا اتمام مییابد.
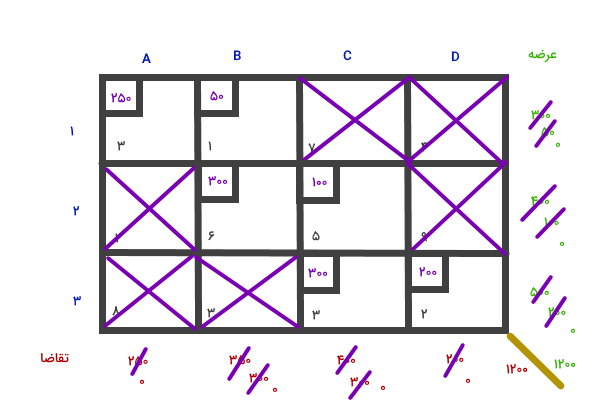
در انتهای مراحل بالا، مسیر حمل و نقل ابتدایی و خانههای دارای تخصیص مشخص میشوند. هزینه این خانهها را در مقدار تخصیص یافته به آنها ضرب کرده و حاصلضربها را جمع میکنیم:
$$
(250 \times 3) + (50 \times 1) + (300 \times 6) + (100 \times 5) + (300 \times 3) + (200 \times 2) = 4400
$$
جواب موجه اولیه بر اساس روش گوشه شمال غربی، برابر 4400 است.
مراحل روش کمترین هزینه
مراحل اجرای روش کمترین هزینه برای به دست آوردن جواب موجه اولیه عبارت هستند از:
- متوازن کردن عرضه و تقاضا
- انتخاب خانه دارای کمترین هزینه (انتخاب دلخواه در صورت وجود چند خانه با کمترین هزینه)
- اختصاص کمترین عرضه یا تقاضا به خانه انتخابی
- کم کردن مقدار اختصاص یافته از عرضه و تقاضا
- حذف سطر یا ستون مقابل عرضه یا تقاضای صفر
- تکرار مراحل بالا برای خانههای باقیمانده تا تمام شدن عرضه و تقاضا
- ضرب هزینه خانههای دارای تخصیص در مقدار تخصیص یافته به آنها و جمع حاصلضربها
مراحل روش تقریبی وگل
جواب موجه اولیه توسط روش تقریبی وگل، طی مراحل زیر به دست میآید:
- متوازن کردن عرضه و تقاضا
- انتخاب دو خانه با کمترین مقدار در هر سطر و ستون و نوشتن اختلاف بین آنها در انتهای سطر یا ستون مرتبط
- انتخاب سطر یا ستون مقابل بزرگترین عدد (از میان اختلافهای محاسبه شده در مرحله قبل)
- انتخاب خانه دارای کمترین هزینه در سطر یا ستون
- اختصاص کمترین مقدار عرضه یا تقاضا به خانه انتخابی
- کم کردن مقدار اختصاص یافته از عرضه و تقاضا
- حذف سطر یا ستون مقابل عرضه یا تقاضای صفر
- تکرار مراحل 2 تا 6 برای خانههای باقیمانده تا تمام شدن اختصاص عرضه و تقاضا
- ضرب هزینه خانههای دارای تخصیص در مقدار تخصیص یافته به آنها و جمع حاصلضربها
روشهای معرفی شده تا به اینجا، فقط جواب موجه اولیه را تعیین میکنند. در صورتی که هدف از حل مسئله حمل و نقل، دستیابی به جواب بهینه (کمترین هزینه ممکن) است.
بررسی بهینگی جواب در مسئله حمل و نقل
در بخش قبلی، روشهای مورد استفاده برای رسیدن به یک جواب موجه اولیه در مسئله حمل و نقل را توضیح دادیم. نتایج به دست آمده از این روشها، الزاما بهینه نیستند. از اینرو، باید بهینگی آنها بر اساس شرط بهینگی مورد بررسی قرار گیرد. یکی از روشهای متداول برای بررسی بهینگی جواب اولیه مسئله حمل و نقل، استفاده از توزیع تعدیل شده دانتزیک یا MODI است.
در روش MODI، ابتدا به هر یک از سطرها و ستونها، یک متغیر اختصاص داده میشود (ui برای سطرها و vj برای ستونها). مجموع اعداد اختصاص یافته به این متغیرها، هزینه مربوط به خانه متناظر با سطر i و ستون j است:
$$
c_{ij} = u_i + v_j
$$
شروع اختصاص عدد به متغیرهای ui و vj برای سطر و ستون به صورت دلخواه صورت میگیرد. در ادامه، با رعایت رابطه بالا و بر اساس هزینه خانههای اساسی (موجود در جواب اولیه)، اختصاص عدد متغیرهای ui و vj برای سطرها و ستونهای ادامه مییابد. پس از تکمیل اختصاص ui و vj، برای خانههای غیر اساسی (خارج از جواب اولیه)، یک متغیر مخصوص به صورت زیر تعریف میشود:
$$
t_{ij} = c_{ij} - ( u_i + v_j)
$$
- cij: هزینه خانه غیر اساسی (با شرط مرحله قبل اشتباه گرفته نشود.)
- ui: عدد اختصاص یافته به متغیر u در سطر i ام
- vj: عدد اختصاص یافته به متغیر v در سطر j ام
پس محاسبه متغیر tij برای تمام خانههای غیر اساسی، شرط بهینگی مورد بررسی قرار میگیرد. اگر حتی یک عدد منفی بین اعداد محاسبه شده وجود داشته باشد، جواب اولیه بهینه نیست. متغیر خروجی در این حالت از میان خانههای دارای tij منفی و متغیر ورودی با توجه به خانههای همسایه انتخاب میشود.

آنالیز حساسیت در تحقیق در عملیات 1
توصیف مسائل واقعی به زبان ریاضی، نیازمند تقریب و سادهسازی مسئله است. هیچ کسی نمیتواند ادعا کند که مدلهایش، به طور صد در صد با پدیدههای واقعی مطابقت دارد و قادر پیشبینی رفتار این پدیدهها با خطای صفر است. در واقعیت، اغلب سیستمها به صورت غیر خطی رفتار میکنند. از اینرو، تعریف مسائل مرتبط با این سیستمها به صورت یک مسئله برنامهریزی خطی، خطای راه حل مسئله را افزایش میدهد. البته این معنای عدم کاربرد یا دقت پایین روشهای خطی تحقیق در عملیات 1 نبوده و فقط نیاز به مطالعه بیشتر بر روی حساسیت این روشها در شرایط مختلف را نشان میدهد.
«تحلیل حساسیت» (Sensitivity Analysis)، ابزاری است که به منظور تاثیر تغییر متغیرهای مستقل بر روی رفتار متغیرهای وابسته مورد استفاده قرار میگیرد. تحلیل حساسیت، کاربرد و اهمیت زیادی در مسائل تصمیمگیری و تحقیق در عملیات 1 دارد. در این مسائل، پس از رسیدن به جواب نهایی (جواب بهینه)، حساسیت راهحل به تغییر دادهها مورد بررسی قرار میگیرد. به طور کلی، دو نوع تحلیل حساسیت در مسائل برنامه ریزی خطی وجود دارد:
- آنالیز حساسیت جواب بهینه نسبت به تغییر منابع
- در مسائل برنامه ریزی خطی، اعداد سمت راست محدودیتهای مسئله با عنوان منابع در دسترس شناخته میشوند.
- آنالیز حساسیت جواب بهینه نسبت به تغییر سود یا هزینه
- در مسائل برنامهریزی خطی، ضرایب متغیرهای تصمیم در تابع هدف، ضریب سود یا زیان را نمایش میدهند.
آنالیز حساسیت معمولا در مباحث انتهایی درس تحقیق در عملیات 1 آموزش داده میشود.
مثال کاربرد آنالیز حساسیت برای تحقیق در عملیات 1
در یک کارخانه، دو ماشین، با صرف زمان مشخص، دو محصول را تولید میکنند. هدف کارخانه، دستیابی به حداکثر سود روزانه است. جدول زیر، اطلاعات مربوط به منابع و سود این مسئله را نمایش میدهد.
| محصول یک | محصول دو | دسترسی روزانه | |
| ماشین یک | 2 ساعت | 1 ساعت | 8 ساعت |
| ماشین دو | 1 ساعت | 2 ساعت | 8 ساعت |
| سود | 300 واحد | 200 واحد |
اگر تعداد تولید روزانه محصول یک را با x1 و تعداد تولید روزانه محصول دو را با x2 مشخص کنیم، مدل برنامه ریزی خطی برای مسئله به شکل زیر نوشته میشود:
$$
\begin{array}{rr}
\\Max & z=300 x_{1}+200 x_{2} \\
\text { s.t. } & 2 x_{1}+ x_{2} \leq 8 \\
& x_{1}+2 x_{2} \leq 8 \\
& x_{i} \geq 0 \space(i=1,2)
\end{array}
$$
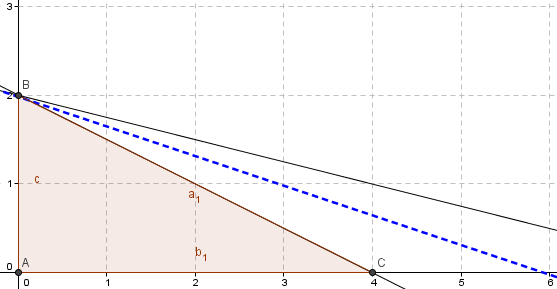
معادله بالا را به روش ترسیمی حل میکنیم. در تصویر زیر، خروجی روش ترسیمی و جواب بهینه در این تصویر مشخص شده است.
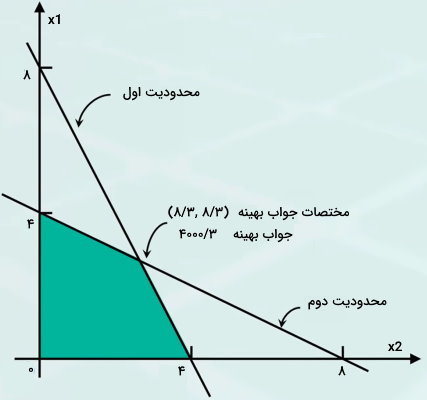
اکنون میخواهیم تحلیل حساسیت جواب بهینه بالا را نسبت به منابع (ساعت در دسترس بودن ماشینها) بررسی کنیم. در مدل ریاضی مسئله، ساعت در دسترس بودن ماشین یک را به 9 افزایش میدهیم. به این ترتیب، داریم:
$$
\begin{array}{rr}
\\Max & z=300 x_{1}+200 x_{2} \\
\text { s.t. } & 2 x_{1}+ x_{2} \leq 9 \\
& x_{1}+2 x_{2} \leq 8 \\
& x_{i} \geq 0 \space(i=1,2)
\end{array}
$$
تصویر زیر، جواب بهینه مسئله بالا را نمایش میدهد.
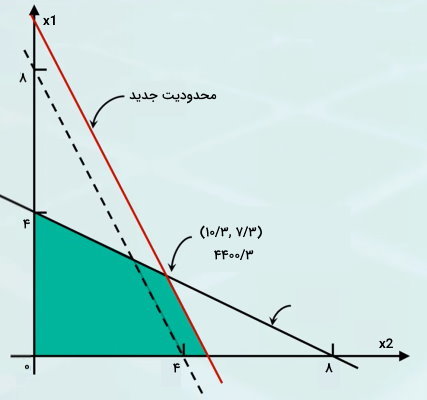
همانطور که مشاهده میکنید، با افزایش ساعت در دسترس بودن ماشین یک، منطقه موجه جواب و جواب بهینه افزایش مییابد. تاثیر تغییر ساعت دسترسی به ماشین یک به جواب بهینه برابر است با:
$$
\frac {4000/3 - 4400/3} {9-8} = 133
$$
رابطه بالا، قیمت سایه را نشان میدهد. بر اساس عدد به دست آمده، افزایش یک ساعته ظرفیت ماشین یک، به میزان 133 واحد در ساعت سودآوری بیشتر دارد. اگر دسترسی به ماشین یک را در مدل ریاضی به مقدار قبلی (8) باز گردانیم و این بار، دسترسی به ماشین دو را به 9 تغییر دهیم، قیمت سایه برابر با 33 واحد در ساعت خواهد بود. همانطور که مشاهده میکنید، با افزایش یک واحدی زمان دسترسی هر ماشین، میزان افزایش سودآوری متفاوت است.
بر اساس این نتایج، اگر قرار به افزایش ظرفیت و دسترسی به یک ماشین باشد، به احتمال زیاد (بسته به هزینههای سرمایهگذاری و نگهداری)، ماشین یک در اولویت قرار میگیرد. این مثال، فقط بخش کوچکی از کاربردها و اهمیت آنالیز حساسیت در مسائل تحقیق در عملیات را نمایش میدهد.
بهترین کتاب ها و منابع آموزشی تحقیق در عملیات 1
اهمیت بالا و کاربرد گسترده، موجب تالیف آثار متعددی در زمینه روشهای اجرای تحقیق در عملیات شده است. برخی از کتابها، مبانی تحقیق در عملیات 1 را به طور کلی و فارغ از حوزه به کارگیری مورد بررسی قرار میدهند.
برخی دیگر، بر روی کاربردهای تحقیق در عملیات بر روی یک حوزه، رشته یا گرایش خاص تمرکز میکنند. از شناخته شدهترین و بهترین کتابهای بینالمللی تحقیق در عملیات 1 میتوان به موارد زیر اشاره کرد:
- «Operations Research: An Introduction» نوشته «Hamdy A. Taha»
- «Operations Research: Applications and Algorithms» نوشته «Wayne L. Winston»
- «Introduction to Operations Research» نوشته «Frederick S Hillier و Gerald J. Lieberman»
- «Linear Programming: Foundations and Extensions» نوشته «Robert J. Vanderbei»
- «Schaum's Outline of Operations Research» نوشته «Richard Bronson»
برخی از کتابهای معروف تحقیق در عملیات 1 به زبان فارسی نیز عبارت هستند از:
- تحقیق در عملیات 1 نوشته زاهدی سرشت
- تحقیق در عملیات 1 نوشته عادل آذر (انتشارات پیام نور)
- تحقیق در عملیات 1 نوشته امیر ایمن پور
- تحقیق در عملیات 1 نوشته احسان خاکبازان
ابزارها و نرم افزارهای تحقیق در عملیات 1
امروزه، با گسترش ابزارهای کامپیوتری و بهبود توان پردازشی کامپیوترها، حل مسائل پیچیده ریاضی ساده شدهاند. نرم افزارهای کامیپوتری، ابزارهای بسیار مناسب و دقیقی هستند که کارشناسان تحقیق در عملیات را از انجام محاسبات دستی بینیاز میکنند. از پرکاربردترین و بهترین گزینههای موجود برای حل مسائل تحقیق در عملیات 1 میتوان به موارد زیر اشاره کرد:
- MATLAB
- Lingo
- Gurobi
- CPLEX
- GAMS
- Visum
- R Project
- GLPK
- OpenSolver
فرادرس، چندین آموزش جامع و کاربردی را در رابطه با یادگیری ابزارهای تحقیق در عملیات تهیه کرده است. در فهرست زیر، عناوین برخی از این آموزشها را آوردهایم:
- فیلم آموزش برنامهریزی خطی Simplex در متلب و حل مسئله حمل و نقل
- فیلم آموزش پیاده سازی نظریه بازی یا گیم تئوری Game Theory در متلب MATLAB
- فیلم موزش رتبه بندی Rating با روش تخصیص خطی Linear Assignment در متلب
- فیلم آموزش نرم افزار بهینه سازی لینگو LINGO
- فیلم آموزش حل مسائل برنامهریزی خطی با نرم افزار Lindo Lingo
- فیلم آموزش تحلیل و طراحی شبکه های حمل و نقل با Visum
- فیلم آموزش نرم افزار گمز GAMS
سخن پایانی: تحقیق در عملیات 2 و 3
در این مقاله، اصول ابتدایی و برخی از روشهای مهم برای حل مسائل تحقیق در عملیات را مرور کردیم. مباحث ارائه شده در این مطلب، فقط بخشی از مباحث گسترده تحقیق در عملیات 1 بودند که بر روی برنامه ریزی خطی تمرکز داشتند. در درسهای تحقیق در عملیات 2 و تحقیق در عملیات 3، روشهای دیگری نظیر برنامه ریزی عدد صحیح، برنامه ریزی صفر و یک (تخصیص)، برنامه ریزی پویا، برنامه ریزی غیر خطی و تحلیل شبکهها مورد بررسی قرار میگیرند. فرادرس، در رابطه با این دروس نیز چند فیلم آموزشی تهیه کرده است که میتوانند در یادگیری کامل دروس تحقیق در عملیات و آمادگی برای آزمونهای مختلف به شما کمک کنند. عناوین این آموزشها عبارت هستند از:











جناب آقای حسین زبرجدی دانا از توضیحات کامل شما سپاسگزارم. خیر ببینی. دستهات پر از طلا