تابع جریان در سیالات — به زبان ساده

در این مطلب قصد داریم تا نحوه بدست آوردن و تحلیل شکل یک جریان را توضیح دهیم. البته پیش‌تر در وبلاگ فرادرس عنوان شد که معادله ناویر-استوکس ابزاری است که می‌توان با استفاده از آن کمیت‌های مختلف هر جریانی را تحلیل کرد. با این حال،‌ در این مطلب با معرفی مفهوم تابع جریان روشی هموارتر را بیان خواهیم کرد. لازم به ذکر است که قبل از مطالعه این مطلب پیشنهاد می‌شود مطالب پیوستگی و بقای جرم در سیالات، معادلات ناویر استوکس و سینماتیک سیالات مطالعه شوند.

تابع جریان

همان‌طور که در مطلب معادله ناویر-استوکس نیز بیان شد، همواره به منظور بدست آوردن شکل یک جریان، بایستی معادله مذکور حل شود. همان‌طور که می‌دانید معادله ناویر-استوکس، نتیجه‌ای از معادلات بقا و مومنتوم در سیالات محسوب می‌شود. از این رو تابعی تحت عنوان «تابع جریان» (Stream Function) یا  $$\psi$$ به نحوی تعریف می‌شود تا معادله بقا جرم را ارضا کند.

فیلم آموزش مکانیک سیالات – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

در ابتدا لازم است یادآوری کنیم که معادله پیوستگی یا بقا جرم به صورت زیر است.

$$\large { \frac { \partial u } { \partial x } } + { \frac { \partial v } { \partial y } } = 0$$

در معادله بالا u، سرعت در راستای x و v سرعت در راستای y هستند. حال اگر تابع $$\psi$$ به صورت زیر تعریف شود، می‌تواند معادله فوق را ارضا کند.

$$\large {\displaystyle u = { \frac { \partial \psi } { \partial y } } }$$

$$\large {\displaystyle v = - { \frac { \partial \psi } { \partial x } } }$$

به منظور بررسی می‌توان سرعت‌های تعریف شده در بالا را در معادله پیوستگی قرار داد. با انجام این کار، معادله پیوستگی به صورت زیر برقرار می‌شود.

$$ \large { \frac { \partial } { \partial x } } ( \frac { \partial \psi } { \partial y } ) + { \frac { \partial } { \partial y } } ( - \frac { \partial \psi } { \partial x } ) \  = 0 $$

بنابراین روابط در نظر گرفته شده برای u و v معادله پیوستگی را ارضا می‌کند. با این تعریف میدان برداری سرعت را نیز می‌توان به صورت زیر در نظر گرفت.

$$\large {\displaystyle V = i { \frac { \partial \psi } { \partial y } } } - j { \frac { \partial \psi } { \partial x } }$$

از طرفی رابطه مربوط به کرل میدان سرعت بر حسب تابع جریان را می‌توان به صورت زیر بیان کرد:

$$\large \nabla × V = -k \nabla ^ 2 \psi \ \ \ , \ \ \nabla ^ 2 \psi = \frac { \partial ^ 2 \psi } { \partial x ^ 2 } + \frac { \partial ^ 2 \psi } { \partial y ^ 2 }$$

هم‌چنین می‌دانید که شکل معادله ناویر-استوکس به صورت زیر است.

$$\large \rho \frac { d V } { d t } = \rho g - \nabla p + \mu \nabla ^ 2 V$$

اگر از تابع فوق کرل بگیریم،‌ می‌توانیم آن را بر حسب $$\psi$$، به شکل زیر بازنویسی کنیم.

$$\large { \frac { \partial \psi } { \partial y } } { \frac { \partial } { \partial x } } ( \nabla ^ 2 \psi ) - { \frac { \partial \psi } { \partial x } } { \frac { \partial } { \partial y } } ( \nabla ^ 2 \psi ) = \nu \nabla ^ 2 (\nabla ^ 2 \psi )$$
معادله ۱

در رابطه فوق، $$\nu = \mu / \rho$$، ویسکوزیته سینماتیکی نامیده می‌شود. رابطه فوق از یک جهت مفید و از جهتی دیگر معادله‌ای مشکل است. مزیت این معادله، اسکالر بودن آن و البته تک تابعی بودنش است. این در حالی است که معادله از مرتبه ۴ بوده، در نتیجه حل آن به نسبت مشکل خواهد بود.

با حل کردن رابطه فوق برای یک جریان، تابع $$\psi$$ بدست آمده و نهایتا می‌توان سرعت‌های u و v را نیز بدست آورد. بدیهی است که برای معادله دیفرانسیل فوق، به ۴ شرط مرزی نیاز داریم. برای نمونه برای جریان یکنواختی که روی یک جسم جامد عبور می‌کند، این چهار شرط مرزی به صورت زیر هستند.

در دور دست، تنها سرعت در راستای افقی وجود داشته بنابراین در بینهایت شرط مرزی به شکل زیر است. توجه داشته باشید که فرض بر این است، جریان به صورت افقی روی یک جسم عبور می‌کند.

$$\large { \displaystyle U _ \infty = { \frac { \partial \psi } { \partial y } } } \ \ , \ \ { \displaystyle 0 = { \frac { \partial \psi } { \partial x } } }$$

با توجه به صفر بودن سرعت روی جسم، شرط مرزی در آن برابر است با:

$$\large { \displaystyle { \frac { \partial \psi } { \partial x } } = { \frac { \partial \psi } { \partial y } } } = 0$$

با استفاده از روش‌های CFD معادله ۱ را در بسیاری از موارد حل می‌کنند. در موارد خاصی که جریان غیرقابل تراکم و غیرلزج باشد، کرل میدان سرعت برابر با صفر بوده و رابطه ۱ ساده‌تر می‌شود. در چنین مواردی معادله ۱ به صورت زیر در می‌آید.

$$\large \nabla ^ { 2 } \psi =0 \Rightarrow \frac { \partial ^ 2 \psi } { \partial x ^ 2 } + \frac { \partial ^ 2 \psi } { \partial y ^ 2 }$$

رابطه فوق، معادله لاپلاس بوده که حل‌های تحلیلی زیادی برای آن ارائه شده است.

مفهوم هندسی تابع جریان

تعریف ریاضیاتیِ تابع جریان $$\psi$$ می‌تواند ما را به یک مفهوم هندسی برساند. خطوط $$\psi$$ ثابت، در حقیقت نشان دهنده خطوط جریان هستند. بنابراین این خطوط همچون مرز جامد عمل کرده و هیچ شار جرمی از آن‌ها عبور نمی‌کند. از مفاهیم پایه‌ای سیالات می‌دانید که در طول یک خط جریان، رابطه زیر برقرار است.

$$\large \frac {d x } { u } = \frac {d y } { v }$$

فیلم آموزش مکانیک سیالات ۱ – مرور و حل تمرین – بخش اول در فرادرس

کلیک کنید

رابطه فوق را می‌توان به صورت زیر نیز بیان کرد:

$$\large u d y - v d x = 0$$

با جایگذاری $$\psi$$ در رابطه فوق، داریم:

$$\large \frac { \partial \psi } { \partial x } d x + \frac { \partial \psi } { \partial y } d y = 0 = d \psi$$

بنابراین با بدست آوردن تابع $$\psi ( x , y )$$ می‌توان شکل خطوط جریان را حدس زد. در شکل زیر نمونه‌ای از یک خط جریان نشان داده شده است.

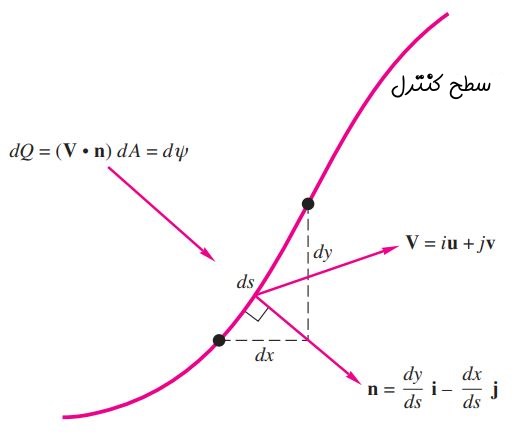
توجه داشته باشید که $$\psi$$ را می‌توان متناسب با اندازه دبی جریان در نظر گرفت. در حقیقت برای سطح کنترل A، رابطه زیر را می‌توان بین دیفرانسیل dQ و $$\psi$$ بیان کرد:

$$\large \begin{align*} d Q = (V.n) d A = ( i \frac {\partial \psi} { \partial y } - j \frac { \partial \psi} { \partial x } ) ( i \frac { dy } { ds } - j \frac { dx } { ds } ) d s \large = \frac { \partial \psi } { \partial x } d x + \frac { \partial \psi } { \partial y } d y = d \psi \end{align*}$$

بنابراین تغییرات $$\psi$$ نشان دهنده تغییر دبی جریان است. برای نمونه اشکال زیر، دو حالت مختلف را برای جریان عبوری نشان می‌دهد.

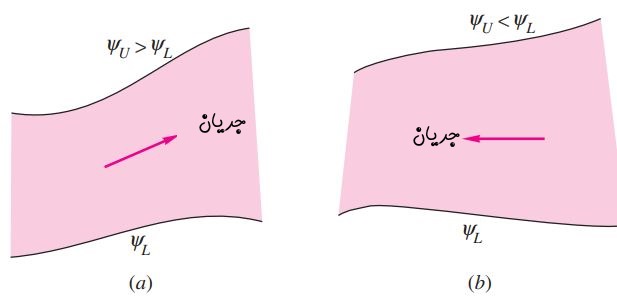
فرض کنید در شکل فوق، سطح پایین با ۱ و سطح بالا با ۲ نامیده شده باشد. در این صورت دبی جریان عبوری از سطح را می‌توان به صورت زیر محاسبه کرد.

$$\large Q _ { 1 \rightarrow 2 } = \int _ 1 ^ 2 ( V . n ) d A = \int _ 1 ^ 2 d \psi = \psi _ 2 - \psi _ 1$$

هم‌چنین همان‌طور که در شکل ۱ نیز نشان داده شده، جهت جریان را می‌توان با توجه به افزایشی یا کاهشی بودن تابع جریان، تعیین کرد.

مثال ۱

فرض کنید رابطه مربوط به میدان سرعت برای یک جریان به صورت زیر باشد. با این فرض، شکل خطوط جریان را برای میدان مربوطه ترسیم کنید.

$$\large u = a ( x ^ 2 - y ^ 2 ) \ \ \ , \ \ \ v=-2axy \ \ \ , \ \ \ w = 0$$

در قدم اول بایستی صادق بودن میدان فوق در معادله پیوستگی را بررسی کرد. با قرار دادن میدان فوق در معادله پیوستگی داریم:

$$\large \frac { \partial u } { \partial x } + \frac { \partial v } { \partial y } =\frac { \partial u } { \partial x } [a ( x ^ 2 - y ^ 2 ) ] + \frac { \partial } { \partial y } ( - 2 a x y ) = 2 a x + ( - 2 a x ) = 0$$

بنابراین ما نشان دادیم که می‌توان برای این جریان یک تابع جریان نوشت. برای بدست آوردن تابع جریان، مطابق با رابطه زیر از تعریف استفاده می‌کنیم.

$$\large u = \frac { \partial \psi } { \partial y } = a x ^ 2 - a y ^ 2$$
معادله ۲

$$\large v = -\frac { \partial \psi } { \partial x } = - 2 a x y$$
معادله ۳

با انتگرال‌گیری از معادله 2 داریم:

$$\large \psi = a x ^ 2 y - \frac { a y ^ 3 } { 3 } + f ( x )$$

با مشتق‌گیری از رابطه فوق و قرار دادن آن در معادله ۳، داریم:

$$\large \frac { \partial \psi } { \partial x } = 2 a x y + f ^ { \prime } ( x ) = 2 a x y$$

حال از رابطه فوق نسبت به x مشتق گرفته و آن را برابر با معادله ۲ قرار می‌دهیم. در این صورت $$\psi$$ به صورت زیر بدست خواهد آمد.

$$\large \psi = a ( x ^ 2 y - \frac { y ^ 3 } { 3 } ) + C$$

به منظور رسم تابع جریان بدست آمده C=0 در نظر می‌گیریم (C عددی انتخابی است که می‌تواند هر عددی در نظر گرفته شود). در این صورت با انتخاب $$\psi$$های مختلف، شکل‌های متفاوتی از خطوط جریان بدست می‌آید. در شکل زیر خطوط جریان متناسب با تابع جریان بدست آمده، نشان داده شده.

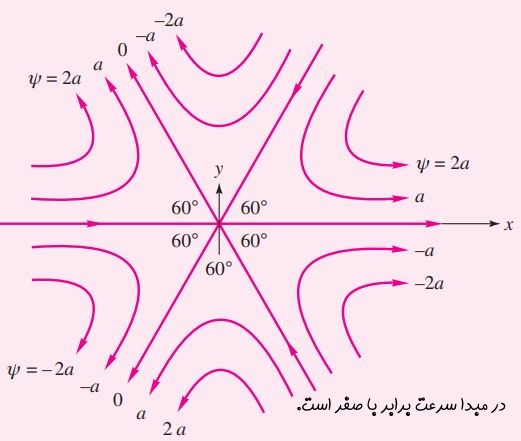
احتمالا حدس زده‌اید که معادله بدست آمده، خطوط جریان برخوردی به یک زاویه ۶۰ درجه را نشان می‌دهد. بنابراین هریک از حالات زیر می‌تواند در نتیجه تابع جریان بدست آمده باشد.

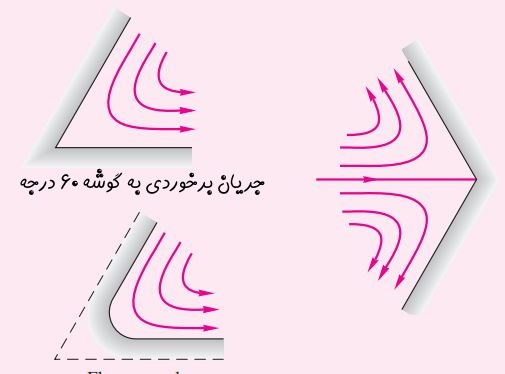
در این مطلب تنها مفهوم خط جریان و یک مثال از تابع جریان ارائه شد. در آینده و در مطلب تابع پتانسیل انواع مختلف خطوط جریان از جمله «منبع» (Source)، «چاه» (Sink)، «دوقطبی» (Doplet) را مورد بررسی قرار خواهیم داد.

^^