هنگامی که افراد می‌خواهند کارهای علمی را در زبان برنامه‌نویسی پایتون (Python Programming Language) انجام دهند، اولین کتابخانه‌ای که می‌توان از آن استفاده کرد «سای‌پای» (SciPy) است. همان‌طور که در مطلب بهینه سازی در پایتون بیان شده است، سای‌پای فقط یک کتابخانه نیست، بلکه اکوسیستم کاملی از کتابخانه‌ها است که با یکدیگر کار می‌کنند تا به افراد در انجام وظایف علمی پیچیده به صورت سریع و قابل اعتماد کمک کنند.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

متمایز کردن اکوسیستم SciPy و کتابخانه SciPy

هنگامی که کاربر قصد دارد از پایتون برای وظایف محاسبات کامپیوتری استفاده کند،‌ چندین کتابخانه وجود دارد که استفاده از آن‌ها به او توصیه می‌شود.

فیلم آموزش کتابخانه های NumPy و Matplotlib در پایتون در فرادرس

کلیک کنید

این کتابخانه‌های پایتون عبارتند از:

نام‌پای (NumPy)
سای‌پای (SciPy)
مت‌پلات‌لیب (Matplotlib)
آی‌پایتون (IPython)
سیم‌پای (SymPy)
پانداس (Pandas)

این کتابخانه‌ها در کنار هم، اکوسیستم سای‌پای را می‌سازند و برای آن طراحی شده‌اند که در کنار یکدیگر کار کنند. بسیاری از این موارد به طور مستقیم برای انجام محاسبات بر آرایه‌های نام‌پای تکیه دارند.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

در این راهنما، فرض شده است که کاربر با ساخت آرایه‌های نام‌پای و انجام پردازش‌هایی روی آن‌ها آشنایی دارد. به کاربرانی که با کتابخانه نام‌پای به خوبی آشنایی ندارند‌، مطالعه مطالب زیر توصیه می‌شود.

فیلم آموزش هوش مصنوعی – مقدماتی در فرادرس

کلیک کنید

همچنین، برای مطالعه بیشتر پیرامون کتابخانه‌های هوش مصنوعی و علم داده پایتون، مطالعه مطالب زیر پیشنهاد می‌شود.

در مطلب بهینه سازی در پایتون کتابخانه سا‌ی‌پای که یکی از مولفه‌های اساسی اکوسیستم سای‌پای محسوب می‌شود مورد بررسی قرار گرفته است. کتابخانه سای‌پای یک کتابخانه بنیادی برای محاسبات علمی در پایتون است. این کتابخانه، رابط‌های بسیار موثر و کاربرپسندی برای وظایفی مانند «انتگرال عددی» (Numerical Integration)، «بهینه‌سازی ریاضیاتی» (Optimization)، «پردازش سیگنال» (Signal Processing)،‌ جبر خطی (Linear Algebra) و دیگر موارد دارد.

بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

آشنایی با ماژول‌های SciPy

در این بخش از مطلب بهینه سازی با پایتون ماژول‌های SciPy به طور کلی بررسی می‌شوند. کتابخانه سای‌پای ترکیبی از تعدادی از ماژول‌ها است که کتابخانه‌ها را به واحدهای کارکردی متفاوتی تقسیم می‌کنند.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

به افرادی که تمایل دارند پیرامون ماژول‌های گوناگون سای‌پای اطلاعات کسب کنند، استفاده از دستور help() ‎ در سای‌پای توصیه می‌شود. در ادامه، چگونگی اجرای این دستور نمایش داده شده است.

1>>> import scipy
2>>> help(scipy)

استفاده از دستور بالا موجب تولید خروجی‌هایی پیرامون کل کتابخانه سای‌پای می‌شود. بخشی از این خروجی، در ادامه نمایش داده شده است.

-----------

Using any of these subpackages requires an explicit import.  For example,
``import scipy.cluster``.

::

 cluster                      --- Vector Quantization / Kmeans
 fft                          --- Discrete Fourier transforms
 fftpack                      --- Legacy discrete Fourier transforms
 integrate                    --- Integration routines
...

این بلوک کد، بخش Subpackages از خروجی دستور help را نمایش می‌دهد که در واقع، لیستی از همه ماژول‌های موجود در سای‌پای (SciPy) است که برای انجام محاسبات قابل استفاده هستند. متنی که در بالای خروجی نمایش داده شده، شایان توجه است. منظور،‌ این بخش است: «.Using any of these subpackages requires an explicit import». هنگامی که کاربران می‌خواهند از کارکردهای یک ماژول در سای‌پای استفاده کنند، نیاز به وارد کردن (ایمپورت | Import) ماژولی دارد که می‌خواهد از آن استفاده کنند. مثال‌هایی در این رابطه در ادامه مطلب بهینه سازی در پایتون ارائه شده است که به درک بهتر این موضوع کمک می‌کند.

فیلم آموزش بهینه سازی با پایتون – بررسی و حل مسائل تحقیق در عملیات در فرادرس

کلیک کنید

هنگامی که کاربر تصمیم گرفت که از کدام ماژول باید استفاده کند، می‌تواند مرجع رابط‌برنامه‌نویسی کاربردی سای‌پای (SciPy API Reference) را بررسی کند که حاوی همه جزئیات پیرامون هر ماژول در سای‌پای است. همچنین، شایان توجه است که اگر کاربر به دنبال راهنماهایی با توضیحات بیشتر است، استفاده از رونویس سخنرانی‌های انجام شده پیرامون سای‌پای پیشنهاد می‌شود که در وب‌سایت این کتابخانه موجود است. این رونویس‌های سخنرانی‌ها، منابع خوبی برای بررسی عمیق‌تر ماژول‌های پایتون محسوب می‌شوند. در ادامه این راهنما، دو تا از ماژول‌های مهم و کاربردی سای‌پای، یعنی cluster و optimize مورد بررسی قرار خواهند گرفت. اما در ابتدا، کاربر نیاز به نصب کتابخانه سای‌پای روی کامپیوتر خودش دارد.

روش نصب SciPy روی کامپیوتر

در این بخش از مطلب بهینه سازی با پایتون روش نصب SciPy روی کامپیوتر مورد بررسی قرار می‌گیرد.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

درست مانند دیگر بسته‌های پایتون، برای نصب SciPy روی کامپیوتر نیز دو راه اساسی وجود دارد که عبارتند از:

آناکوندا (Anaconda)
PyPI و pip

در ادامه مطلب بهینه سازی در پایتون، روش نصب SciPy با استفاده از هر دو رویکرد بیان شده در بالا، تشریح شده است. تنها پیش‌نیاز و در واقع، وابستگی نرم‌افزاری سای‌پای، کتابخانه نام‌پای است. هر دو روش نصبی که در ادامه مطلب بهینه سازی در پایتون توضیح داده شده‌اند، به طور خودکار علاوه بر کتابخانه سای‌پای، کتابخانه نام‌پای را نیز در صورت نیاز نصب می‌کنند. منظور از عبارت «در صورت نیاز» آن است که اگر نسخه مناسبی از کتابخانه نام‌پای پیش از نصب سای‌پای روی سیستم نصب نشده باشد، طی فرایند نصب و به طور خودکار نصب این کتابخانه نیز انجام می‌شود.

آناکوندا

«توزیع پایتون آناکوندا» (Anaconda Python Distribution) یک توزیع پایتون محبوب است که محبوبیت و معروفیت خود را بیشتر وام‌دار کتابخانه‌های علمی توکار خود برای سیستم‌عامل‌های «ویندوز» (Windows)، «مک‌اواس» (macOS) و «لینوکس» (Linux) است.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در فرادرس

کلیک کنید

آناکوندا برای کاربرانی که پایتون را از پیش روی سیستم خود نصب ندارند، گزینه بسیار مناسبی برای شروع به کار محسوب می‌شود. با نصب کردن آناکوندا، سای‌پای به همراه کلیه کتابخانه‌های مورد نیاز و در واقع وابستگی‌های آن و به صورت پیش‌فرض، روی سیستم کاربر نصب می‌شود.

بنابراین، کاربرانی که آناکوندا را روی سیستم خود نصب دارند، نیازی به نصب کردن چیزی نخواهند داشت و سای‌پای به صورت پیش‌فرض روی سیستم آن‌ها نصب شده است. برای مطالعه بیشتر و تکمیلی پیرامون توزیع پایتون آناکوندا، مطالعه مطالب زیر توصیه می‌شود.

بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

به کاربرانی که در هنگام مطالعه یا پس از مطالعه مطلب بهینه سازی در پایتون قصد نصب آناکوندا را دارند اکیدا توصیه می‌شود که آخرین نسخه از پایتون را نصب کنند. در هنگام اجرای نصاب آناکوندا روی سیستم کاربر، می‌توان روال پیش‌فرض نصب برای برنامه کاربردی آناکوندا را روی سیستم انجام داد.

نکته: کاربران حتما باید به این موضوع توجه داشته باشند که آناکوندا در پوشه‌ای نصب شود که نیازی به دسترس مدیر سیستم (Administrator Permissions) ندارد. این تنظیمات به صورت پیش‌فرض در نصاب وجود دارد.

فیلم آموزش مقدماتی پردازش سیگنال با پایتون Python در فرادرس

کلیک کنید

کاربرانی که آناکوندا را روی سیستم خود نصب دارند، اما قصد دارند سای‌پای را نصب و یا به روز رسانی کنند، می‌توانند این کار را به سادگی و با استفاده از دستوراتی که در ادامه این بخش از مطلب بهینه سازی در پایتون بیان شده است، انجام دهند. کاربر ابتدا باید «ترمینال» (Terminal) را در «مک‌او‌اس» (macOS) یا «لینوکس» (Linux) و یا «آناکوندا پرومت» (Anaconda Prompt) را در ویندوز وارد کند و یکی از خط کدهای زیر را (متناسب با اینکه قصد نصب دارد یا هدف آن به روز رسانی است) وارد و اجرا کند.

1$ conda install scipy
2$ conda update scipy

کاربر باید در صورتی که نیاز به نصب سای‌پای (SciPy) دارد از اولین خط و در صورتی که قصد به روز رسانی سای‌پای نصب شده روی سیستم خود را دارد، از دستور دومی استفاده کند که در بالا ارائه شده است.

1>>> import scipy
2>>> print(scipy.__file__)
3/.../lib/python3.7/site-packages/scipy/__init__.py

در قطعه کدی که در جعبه کد بالا مشاهده می‌شود، کتابخانه سای‌پای (SciPy) وارد (Import | ایمپورت) و محلی که فایل سای‌پای از آن بارگذاری شده نیز چاپ شده است. مثال بالا برای سیستم‌عامل مک‌او‌اس (macOS) است. احتمالا،‌ کامپیوتر کاربر موقعیت متفاوتی را نشان می‌دهد. اکنون، کاربر سای‌پای را روی سیستم خود نصب کرده و این کتابخانه، آماده استفاده است.

فیلم آموزش یادگیری عمیق با پایتون – تنسورفلو و کراس TensorFlow و Keras در فرادرس

کلیک کنید

مخاطبان این مطلب می‌توانند در صورت آشنایی کامل با pip بخش بعدی مطلب بهینه سازی در پایتون یعنی بخش مربوط به Pip را بدون مطالعه رد کنند و مستقیما به مطالعه ادامه مطلب بهینه سازی در پایتون و در واقع بخش‌های مربوط به کتابخانه سای‌پای (SciPy) بپردازند. هر چند به طور کلی، توصیه می‌شه که کل این مطلب به طور کامل توسط مخاطب خوانده شود.

نصب SciPy با استفاده از pip

کاربرانی که در حال حاضر یک نسخه از پایتون را روی سیستم خود نصب دارند ولی نسخه نصب شده توزیع پایتون آناکوندا نیست و یا به طور کلی قصد ندارند که از آناکوندا استفاده کنند، می‌توانند از pip برای نصب سای‌پای استفاده کنند.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

نکته: pip بسته‌ها را با استفاده از فرمتی نصب می‌کند که wheels‌ نامیده می‌شود. در فرمت wheel، کد پیش از ارسال به کامپیوتر کاربر کامپایل می‌شود. این مورد، رویکردی تقریبا مشابه آنچه است که توسط آناکوندا اتخاذ شده است. اگرچه، فرمت فایل‌های wheel اندکی از فرمت فایل‌های آناکوندا متفاوت است و این دو قابل تعویض با یکدیگر نیستند.

برای نصب SciPy‌ با استفاده از pip، ابتدا باید ترمینال را باز و دستور زیر را تایپ کرد.

1$ python -m pip install -U scipy

کدی که در جعبه کد بالا ارائه شده است، در صورتی که کتابخانه سای‌پای روی سیستم کاربر نصب نشده باشد، این کتابخانه را نصب می‌کند. همچنین، در صورتی که سای‌پای از پیش روی سیستم کاربر نصب شده باشد، آن را ارتقا (آپگرید | Upgrade) می‌دهد. برای حصول اطمینان از اینکه کتابخانه پایتون پس از اجرای دستور بالا به درستی نصب شده است، باید پایتون (Python) را در ترمینال اجرا و تلاش کرد تا کتابخانه سای‌پای (SciPy) را وارد (ایمپورت | Import) کرد.

1>>> import scipy
2>>> print(scipy.__file__)
3/.../lib/python3.7/site-packages/scipy/__init__.py

در قطعه کد ارائه شده در بالا، کتابخانه سای‌پای (SciPy) ایمپورت و محل فایلی که از آنجا بارگذاری می‌شود نیز چاپ شده است. مثال بالا برای سیستم‌عامل مک‌اواس و با استفاده از pyenv انجام شده است. کامپیوتر هر کاربری ممکن است آدرس متفاوتی را نشان دهد. اکنون که کتابخانه پایتون سای‌پای با موفقیت روی سیستم کاربر نصب شده است، در ادامه مطلب بهینه سازی در پایتون به این موضوع پرداخته می‌شود که کاربر چگونه می‌تواند با چالش‌هایی مواجه شود که ضمن کار با SciPy با آن‌ها مواجه خواهد شد.

استفاده از ماژول Cluster در کتابخانه SciPy

در این بخش از مطلب بهینه سازی با پایتون روش استفاده از ماژول Cluster در کتابخانه SciPy مورد بررسی قرار گرفته است. «خوشه‌بندی» (Clustering) یکی از روش‌های محبوب موجود برای دسته‌بندی داده‌ها است (استفاده از کلمه دسته‌بندی در اینجا به معنی Classification که از روش‌های یادگیری نظارت شده محسوب می‌شود نیست و صرفا به کار بخش‌بندی داده‌ها اشاره دارد). در خوشه‌بندی، دسته‌بندی داده‌ها با تخصیص آن‌ها به گروه‌های مختلف داده‌ای انجام می‌شود. کتابخانه سای‌پای دارای پیاده‌سازی پیش‌فرضی از الگوریتم‌های خوشه‌بندی گوناگون است.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

از جمله الگوریتم‌های خوشه‌بندی که به طور پیش‌فرض در کتابخانه سای‌پای موجود هستند می‌توان به الگوریتم «K-میانگین» (K-Means) و «الگوریتم‌های خوشه‌بندی سلسله مراتبی» (Hierarchical Clustering Algorithms) اشاره کرد. در مثالی که در این بخش از مطلب بهینه سازی در پایتون ارائه شده است، از الگوریتم K-Means که به طور پیش‌فرض در کتابخانه پایتون SciPy و در scipy.cluster.vq وجود دارد، برای خوشه‌بندی داده‌ها استفاده می‌شود. vq در واقع مخفف «کمی‌سازی برداری» (Vector Quantization | VQ) است.

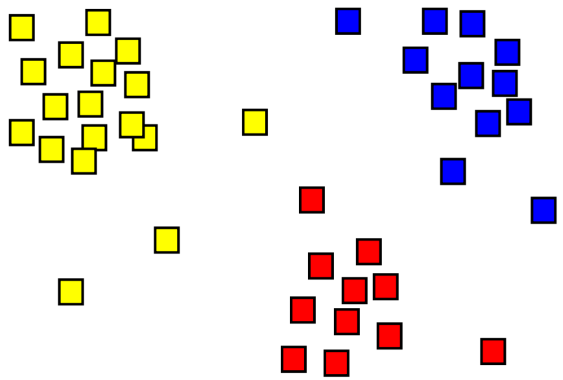
بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

در ادامه این بخش از مطلب بهینه سازی در پایتون ابتدا «مجموعه داده‌ای» (Data Set) که برای مثال بیان شده در این بخش از مطلب بهینه سازی در پایتون مورد استفاده قرار گرفته است به طور اجمالی بررسی می‌شود. این مجموعه داده که با عنوان «SMS Spam Collection Data Set» منتشر شده ، حاوی ۴۸۲۷ پیام کوتاه (Short Message | SMS) واقعی و ۷۴۷ مورد «هرزنامه» (Spam) است. مجموعه داده خام مورد استفاده در اینجا را می‌توان از مخزن یادگیری ماشین دانشگاه کالیفرنیا، ارواین (UCI Machine Learning Repository) دانلود کرد [+].

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

نکته: داده‌های این مجموعه داده توسط «تیاگو اِی آلمیدا» (Tiago A Almeida) و «خوزه ماریه گومز هیدالگو» (José María Gómez Hidalgo) گردآوری شده‌اند. این داده‌ها، در مقاله‌ای با عنوان «مشارکتی در مطالعه فیلترینگ هرزنامه‌ها: مجموعه‌ای جدید و نتایج حاصل شده» (Contributions to the Study of SMS Spam Filtering: New Collection and Results) منتشر شده‌اند. این مقاله در سمپوزیوم مهندسی اسناد ACM سال ۲۰۱۱ (Proceedings of the 2011 ACM Symposium on Document Engineering | DOCENG‘11) منتشر شد که در شهر «مانتین ویو» (Mountain View) واقع در شهرستان «سانتا کلارا» (Santa Clara County) در ایالات متحده آمریکا (USA) برگزار شده بود. برای مطالعه بیشتر پیرامون انواع مجموعه داده‌های رایگان و عمومی قابل دانلود، مطالعه مطالب زیر پیشنهاد می‌شود.

در مجموعه داده SMS Spam Collection Data Set، هر پیام دارای یکی از دو برچسب زیر است:

برچسب «ham» برای پیام‌های «واقعی» و در واقع «درست»
برچسب «spam» برای پیام‌های «هرزنامه» یا «اسپم»

پیام کامل متنی مرتبط با هر چسب نیز در مجموعه داده موجود است. هنگامی که داده‌ها توسط کاربر به طور اجمالی بررسی (Scan)‌ می‌شوند، ممکن است برخی کاربران به این موضوع توجه کنند که پیام‌های هرزنامه حاوی ارقام نوشته شده با عدد زیادی هستند. این پیام‌های هرزنامه معمولا حاوی یک شماره تلفن یا پیام بردن یک جایزه هستند.

فیلم آموزش خوشه بندی با الگوریتم های تکاملی و فراابتکاری در فرادرس

کلیک کنید

در ادامه مطلب بهینه سازی در پایتون با استفاده از کتابخانه SciPy و الگوریتم خوشه‌بندی K-Means که به صورت پیش‌فرض در کتابخانه سای‌پای (SciPy) موجود است، پیش‌بینی خواهد شد که آیا یک پیام هرزنامه است یا خیر و در واقع، پیش‌بینی می‌شود که یک پیام واقعی است یا هرزنامه. این کار، بر اساس تعداد ارقام موجود در پیام متنی کوتاه (SMS) انجام خواهد شد. برای این کار، کاربر باید داده‌ها را بر اساس تعداد ارقام نوشته شده به صورتی عددی در آن‌ها، به سه گروه تقسیم کند. این گروه‌ها در ادامه مورد بررسی قرار گرفته‌اند.

غیر هرزنامه (غیر اسپم): پیام‌هایی با کم‌ترین تعداد ارقام نوشته شده به صورت عدد، به عنوان غیر هرزنامه (واقعی) دسته‌بندی می‌شوند.
ناشناخته: پیام‌هایی با تعداد متوسطی از تعداد ارقام نوشته شده به صورت عدد، در خوشه ناشناخته قرار می‌گیرند و نیاز به آن دارند که توسط الگوریتم‌های پیشرفته‌تری بررسی شوند.
هرزنامه (اسپم): پیام‌هایی با بالاترین تعداد ارقام نوشته شده به صورت عدد، به عنوان هرزنامه (اسپم | Spam) در نظر گرفته می‌شوند.

فیلم آموزش بهینه سازی با پایتون – بررسی و حل مسائل تحقیق در عملیات در فرادرس

کلیک کنید

در ادامه این بخش از مطلب بهینه سازی در پایتون کار دسته‌بندی پیام‌های کوتاه متنی به یکی از سه دسته هرزنامه، غیر هرزنامه و ناشناخته، با خوشه‌بندی پیام‌های متنی انجام می‌شوند. در این راستا، ابتدا باید کتابخانه‌های مورد نیاز برای کار خوشه بندی را وارد (Import) کرد. این کتابخانه‌ها عبارتند از: «پث‌لیب» (Pathlib)، «نام‌پای» (NumPy) و البته، «سای‌پای» (SciPy). در قطعه کد زیر، کار وارد (ایمپورت | Import) کردن کتابخانه‌های مذکور انجام شده است.

from pathlib import Path
import numpy as np
from scipy.cluster.vq import whiten, kmeans, vq

می‌توان مشاهده کرد که در قطع کد بالا، سه تابع (یعنی whiten ، K-Means و vq) از scipy.cluster.vq.‎ وارد شده‌اند. هر یک از این سه تابع، یک آرایه نام‌پای را به عنوان ورودی دریافت می‌کنند. این آرایه‌ها باید حاوی «ویژگی‌های» (Features) مجموعه داده در ستون‌ها و «مشاهدات» (Observations | نمونه‌ها) در سطرهای مجموعه داده باشند.

یک «ویژگی» (Feature) در واقع متغیر جالب توجهی است که توضیحاتی پیرامون داده‌ها (خصوصیت یا ویژگی از داده‌ها) را بیان می‌کند. این در حالی است که یک مشاهده، در واقع یک نمونه است که با ثبت ویژگی‌های آن، ثبت شده است. در این مثال، ۵۵۷۴ مشاهده یا در واقع، پیام کوتاه مستقل از هم وجود دارد. در این مجموعه داده، برای هر نمونه داده (یا در واقع، هر مشاهده) دو ویژگی وجود دارد:

تعداد ارقامی که در پیام متنی موجود هستند
تعداد دفعاتی که تعداد ارقام ثبت شده در کل مجموعه داده تکرار می‌شوند.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

در این مرحله، باید داده‌ها را از پایگاه داده UCI بارگذاری کرد. باید داده‌ها داده‌ها را به عنوان یک فایل متنی بارگذاری کرد. داده‌ها به صورت یک فایل متنی وارد می‌شوند، در حالی که دسته (خوشه) پیام از خود پیام با استفاده از یک کاراکتر tab جدا شده است. در واقع، با نگاه کردن به محتوای فایل متنی مجموعه داده‌ای که بارگذاری می‌شود، می‌توان تعداد ارقام نوشته شده به صورت عددی در هر پیام را همراه با برچسب دسته آن پیام (هرزنامه یا غیر هرزنامه) مشاهده کرد که با ۸ کاراکتر فضای خالی (تب | Tab) از یکدیگر جدا شده‌اند. اکنون باید داده‌ها را با استفاده از pathlib.Path در یک لیست (List) خواند. قطعه کد لازم برای انجام این کار، در ادامه آمده است.

1data = Path("SMSSpamCollection").read_text()
2data = data.strip()
3data = data.split("\n")

در این کد، از pathlib.Path.read_text()‎ برای خواندن فایل به صورت یک رشته (String)، استفاده می‌شود. سپس، از strip()‎. برای حذف هرگونه فضای خالی در امتداد رشته استفاده شده است. همچنین، رشته با استفاده از دستور strip()‎. به یک لیست شکسته می‌شود.

اکنون، می‌توان شروع به تحلیل کردن داده‌ها کرد. در این راستا، باید تعداد ارقام ظاهر شده در هر پیام متنی را شمرد. پایتون در کتابخانه استاندارد خود دارای collections.Counter است که امکان گردآوری (محاسبه) تعداد اشیا در یک ساختار دیکشنری مانند ( Dictionary-Like) را فراهم می‌کند. اگرچه، با توجه به اینکه همه توابع موجود در scipy.cluster.vq آرایه‌های نام‌پای را به عنوان ورودی می‌پذیرند، کاربر نمی‌تواند از collections.Counter برای این مثال استفاده کند. در عوض، از آرایه نام‌پای استفاده و شمارنده به صورت دستی و در واقع از پایه‌، پیاده‌سازی می‌شود.

فیلم آموزش کتابخانه های NumPy و Matplotlib در پایتون در فرادرس

کلیک کنید

باز هم، مسئله‌ای که جالب توجه است تعداد ارقام در یک پیام متنی کوتاه (SMS) داده شده و این است که چه تعداد از پیام‌ها حاوی آن تعداد از ارقام هستند. ابتدا، کاربر باید یک آرایه نام‌پای (NumPy Array) بسازد که مرتبط با تعداد ارقام موجود در یک پیام داده شده و نتیجه وضعیت آن پیام (از جهت اسپم بودن یا نبودن) است.

digit_counts = np.empty((len(data), 2), dtype=int)

در این کد، یک آرایه خالی نام‌پای به نام digit_counts ساخته شده است که دارای دو ستون و ۵۵۷۴ سطر است. تعداد سطرها مساوی با تعداد پیام‌های موجود در مجموعه داده است. کاربر از آرایه digit_counts برای مرتبط کردن تعداد ارقام نوشته شده به صورت عددی در پیام با برچسب آن پیام (اسپم، غیر اسپم و ناشناس) استفاده می‌کند.

در ادامه این بخش از مطلب بهینه سازی در پایتون‌ باید یک آرایه را پیش از وارد کردن حلقه ساخت، بنابراین کاربر نیازی به آن ندارد که با گسترش یافتن آرایه خود، حافظه بیشتری به آن تخصیص دهند. این امر، کارایی کد را بهبود می‌بخشد. سپس، باید داده‌ها را برای ثبت تعداد ارقام و وضعیت پیام پردازش کرد. در این راستا، از قطعه کد زیر استفاده خواهد شد (خط اول کد زیر خط هشتم و خط آخر آن، خط کد شماره دوازده است).

1for i, line in enumerate(data):
2    case, message = line.split("\t")
3    num_digits = sum(c.isdigit() for c in message)
4    digit_counts[i, 0] = 0 if case == "ham" else 1
5    digit_counts[i, 1] = num_digits

در ادامه، روش کار این کد به صورت خط به خط توضیح داده شده است.

خط ۸ کد: حلقه زدن در داده‌ها (Data) انجام می‌شود. در اینجا از enumerate()‎ برا ارزش‌دهی از لیست در line و ساخت اندیس i برای این لیست استفاده شده است.
خط ۹ کد: خط را با استفاده از کاراکتر تب (فضای خالی) برای ساخت case و message می‌شکند. case رشته‌ای است که می‌گوید آیا پیام از نو ham یا spam است؛ در حالی که message رشته‌ای با متن پیام است.
خط ۱۰ کد: تعداد ارقام نوشته شده به صورت عددی در پیام را با استفاده از sum()‎ استفاده می‌کند. هر کاراکتر موجود در پیام با استفاده از isdigit()‎ بررسی می‌شود. سپس، در صورتی که عنصر عددی باشد مقدار True و در غیر این صورت، مقدار False را باز می‌گرداند. پس از آن، sum()‎ با هر مقدار صحیح به عنوان یک (۱) و هر مقدار غلط به عنوان صفر (۰) برخورد می‌کند. بنابراین، نتیجه sum()‎‎ در این ادراکات، تعداد کاراکترها برای موردی است که isdigit()‎ برای آن True بوده است.
خط ۱۱ کد: مقادیر به digit_counts تخصیص پیدا می‌کنند. اگر پیام قانونی (ham) یا مشروع باشد، اولین ستون از سطر i را به 0 متصل می‌کند و اگر پیام هرزنامه یا اسپم بود (Spam) ستون اول از سطر i به ۱ تخصیص داده خواهد شد.
خط ۱۲ کد: مقدار را به digit_counts تخصیص می‌دهد. دومین ستون از سطر i به تعداد ارقام موجود در پیام تخصیص پیدا می‌کند.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

اکنون، آرایه نام‌پای حاوی تعداد ارقام موجود در هر پیام ساخته شده است. در این وهله، کاربر باید الگوریتم خوشه‌بندی را روی یک آرایه اعمال کند که حاوی تعداد پیام‌ها با تعداد دقیق ارقام نوشته شده به صورت عددی در آن‌ها است. به بیان دیگر، کاربر نیاز به ساخت یک آرایه دارد که در آن، اولین ستون دارای تعداد ارقام نوشته شده به صورت عدد در پیام است و دومین ستون، تعداد پیام‌هایی است که حاوی تعداد ارقام نوشته شده به صورت عدد هستند. در این راستا، می‌توان از کد زیر استفاده کرد.

1unique_counts = np.unique(digit_counts[:, 1], return_counts=True)

np.unique()‎ یک آرایه را به عنوان اولین آرگومان دریافت می‌کند و یک آرایه دیگر را با عناصر یکتا از آرگومان باز می‌گرداند. همچنین، چندین آرگومان اختیاری را دریافت می‌کند. در اینجا، از return_counts=True برای یاد دادن این موضوع به np.unique()‎ استفاده می‌شود تا یک آرایه را با تعداد دفعاتی که یک عنصر یکتا در آرایه ورودی ظاهر می‌شود بازگرداند. این دو خروجی، به عنوان یک تاپل (Tuple) بازگردانده می‌شوند که در unique_counts ذخیره شده است. سپس، نیاز به تبدیل unique_counts به شکلی است که برای خوشه‌بندی مناسب محسوب می‌شود.

1unique_counts = np.transpose(np.vstack(unique_counts))

باید با استفاده از np.vstack()‎، دو خروجی 1xN از np.unique()‎ را به یک آرایه 2xN تبدیل کرد و سپس، آن‌ها را به یک آرایه Nx2 انتقال داد. این قالب چیزی است که کاربر در تابع خوشه‌بندی مورد استفاده قرار می‌دهد. پس از انجام این کار، هر سطر در unique_counts حاوی دو عنصر است که در ادامه بیان شده‌اند.

تعداد ارقام نوشته شده به صورت عددی در پیام
تعداد پیام‌هایی که دارای تعداد ارقام نوشته شده به صورتی عددی هستند.

یک زیرمجموعه از خروجی از این دو عملیات، در ادامه نمایش داده شده است.

1[[   0 4110]
2 [   1  486]
3 [   2  160]
4 ...
5 [  40    4]
6 [  41    2]
7 [  47    1]]

در مجموعه داده، ۴۱۱۰ پیام وجود دارد که هیچ تعدادی رقم ندارند؛ ۴۸۶ مورد تنها یک رقم دارند و به همین صورت. اکنون، کاربر باید الگوریتم خوشه‌بندی K-Means را روی این آرایه اعمال کند.

1whitened_counts = whiten(unique_counts)
2codebook, _ = kmeans(whitened_counts, 3)

در اینجا ازwhiten() ‎ برای نرمال کردن هر ویژگی برای داشتن واریانس واحد استفاده شده است. این کار، نتایج حاصل از تابع خوشه‌بندی kmeans()‎ را بهبود می‌بخشد. پس از نرمال‌سازی ویژگی‌ها با تابعwhiten() ‎ به منظور داشتن واریانس واحد، kmeans()‎ داده‌های پاک‌سازی شده و تعداد خوشه‌ها را به منظور ساخت خوشه‌ها و به عنوان آرگومان ورودی، دریافت می‌کند. در این مثال، نیاز به ساخت سه خوشه است. دلیل ساخت سه خوشه همانطور که پیش از این نیز گفته شد، داشتن سه پوشه هرزنامه (اسپم)، غیر هرزنامه و ناشناخته است. kmeans()‎ دو مقدار را باز می‌گرداند. این دو مقدار، در ادامه به طور کامل تشریح شده‌اند.

یکی از مقادیری که kmeans()‎ بازمی‌گردارند، یک آرایه با سه سطر و دو ستون است که «مرکزوار» (Centroids) هر گروه را نشان می‌دهد. الگوریتم kmeans()‎ موقعیت بهینه برای مرکزوار هر خوشه را با کمینه کردن فاصله از مشاهدات به هر مرکزوار، محاسبه می‌کند. این آرایه به codebook تخصیص پیدا می‌کند.
میانه فاصله اقلیدسی از مشاهدات به مرکزوار دیگر چیزی است که توسط تابع kmeans()‎ بازگردانده می‌شود. کاربر نیازی به این مقدار برای کل این مثال ندارد، بنابراین می‌تواند آن را به _ تخصیص دهد.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

در ادامه مثال مطلب بهینه سازی در پایتون کاربر باید با استفاده از ()vq مشخص کند که هر مشاهده به کدام خوشه تعلق دارد.

1codes, _ = vq(whitened_counts, codebook)

()vq کدها را از codebook به هر مشاهده تخصیص می‌دهد. این تابع نیز دو مقدار را در خروجی باز می‌گرداند.

اولین مقدار، آرایه‌ای با طول مشابه با unique_counts است که در آن، مقدار هر عنصر یک عدد صحیح است که نشان می‌دهد هر مشاهده به کدام خوشه تخصیص پیدا کرده است. با توجه به اینکه از سه خوشه در این مثال استفاده شده است، هر مشاهده به خوشه ۰،‌ ۱ یا ۲ تخصیص پیدا می‌کند.
دومین مقدار، آرایه‌ای از فاصله اقلیدسی بین هر مشاهده و مرکزوار آن است.

اکنون که داده‌ها خوشه‌بندی شدند، باید از این داده‌ها برای انجام پیش‌بینی پیرامون پیام‌های کوتاه (SMS) استفاده شود. می‌توان شمارش‌ها را برای تعیین این بررسی کرد که الگوریتم خوشه‌بندی از چه عددی به بعد برای جدا کردن خوشه پیام‌های هرزنامه، غیر هرزنامه و ناشناس استفاده می‌کند. الگوریتم خوشه‌بندی به طور تصادفی کدهای ۰، ۱ و ۲ را تخصیص می‌دهد. بنابراین کاربر می‌تواند تشخیص دهد که کدام به کدام است. می‌توان از این کد برای پیدا کردن کد اختصاص یافته به هر خوشه استفاده کرد:

1ham_code = codes[0]
2spam_code = codes[-1]
3unknown_code = list(set(range(3)) ^ set((ham_code, spam_code)))[0]

در این کد، اولین خط، کدهای تخصیص یافته به پیام‌های سالم را پیدا می‌کند. مطابق با نظریه ارائه شده در بالا، پیام‌های سالم دارای کمترین تعداد ارقام هستند و آرایه ارقام از کمترین تا بیشترین ارقام ذخیره شده است. بنابراین، خوشه پیام‌های سالم از آغاز کد شروع می‌شود.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

به طور مشابه، پیام‌های هرزنامه دارای بیشترین تعداد ارقام هستند و بنابراین، آخرین خوشه در codes را شکل می‌دهند. بنابراین، کد برای پیام‌های هرزنامه با آخرین عنصر از codes برابر خواهد بود. در نهایت، کاربر نیاز به آن دارد که کد مربوط به پیام‌های ناشناخته یا همان Unknown Messages را پیدا کند. با توجه به آنکه تنها سه گزینه برای کد وجود دارد و در حال حاضر دو مورد از آن‌ها شناسایی شده است، می‌توان از عملگر symmetric_difference در پایتون set برای تعیین آخرین مقدار کد استفاده کرد. سپس، کاربر می‌تواند خوشه مربوط به هر نوع پیام را چاپ کند.

1print("definitely ham:", unique_counts[codes == ham_code][-1])
2print("definitely spam:", unique_counts[codes == spam_code][-1])
3print("unknown:", unique_counts[codes == unknown_code][-1])

در قطعه کد بالا، هر خط سطری را در unique_counts پیدا می‌کند که در آن، vq()‎ مقادیر متفاوتی از کد را تخصیص داده است. با توجه به آنکه این عملگر یک آرایه را در خروجی باز می‌گرداند، باید آخرین سطر از آرایه را برای تعیین بالاترین عدد از ارقام تخصیص پیدا کرده به هر خوشه دریافت کرد. خروجی در زیر نمایش داده شده است.

definitely ham: [0  4110]
definitely spam: [47  1]
unknown: [20 18]

در این خروجی، می‌توان مشاهده کرد که پیام‌های قطعا سالم (Definitely Ham) پیام‌هایی با صفر رقم در پیام هستند؛ پیام‌های ناشناخته (Unknown) دارای ارقامی بین ۱ تا ۲۰ در متن خود هستند و پیام‌های قطعا هرزنامه (Definitely Spam) دارای متن پیام‌هایی با ۲۱ تا ۴۷ رقم هستند که این تعداد، بیشترین تعداد ارقام در مجموعه داده محسوب می‌شود. اکنون، باید بررسی کرد که پیش‌بینی‌های انجام شده روی مجموعه داده، چقدر صحیح هستند. ابتدا باید ماسک‌هایی برای digit_counts ساخته شود تا به سادگی بتوان وضعیت ham یا spam پیام‌ها را دریافت کرد.

1digits = digit_counts[:, 1]
2predicted_hams = digits == 0
3predicted_spams = digits > 20
4predicted_unknowns = np.logical_and(digits > 0, digits <= 20)

در این کد، ماسک predicted_hams ساخته می‌شود که در آن، هیچ رقمی داخل پیام وجود ندارد. سپس، ماسک predicted_spams برای همه پیام‌های دارای بیش از ۲۰ رقم ساخته می‌شود. در نهایت، پیام‌های موجود در میانه، predicted_unknowns هستند. سپس، این ماسک‌ها به شمارش ارقام کنونی اعمال می‌شوند تا پیش‌بینی‌ها بازیابی شوند.

1spam_cluster = digit_counts[predicted_spams]
2ham_cluster = digit_counts[predicted_hams]
3unk_cluster = digit_counts[predicted_unknowns]

در اینجا، ماسک‌هایی که کاربر در آخرین بلوک کد ساخته است را روی آرایه digit_counts اعمال می‌کنند. این کار موجب ساختن سه آرایه جدید، تنها با پیام‌هایی می‌شود که در هر سه گروه خوشه‌بندی شده‌اند. در نهایت، می‌توان مشاهده کرد که چه تعداد از هر نوع پیام در هر خوشه افتاده‌اند.

1print("hams:", np.unique(ham_cluster[:, 0], return_counts=True))
2print("spams:", np.unique(spam_cluster[:, 0], return_counts=True))
3print("unknowns:", np.unique(unk_cluster[:, 0], return_counts=True))

این کد، شمارش هر مقدار یکتا از خوشه‌ها را چاپ می‌کند. باید به خاطر داشت که ۰ در اینجا به معنای پیام سالم (ham) و ۱ به معنای پیام هرزنامه (spam) است. نتایج در ادامه نمایش داده شده‌اند.

1hams: (array([0, 1]), array([4071,   39]))
2spams: (array([0, 1]), array([  1, 232]))
3unknowns: (array([0, 1]), array([755, 476]))

در این خروجی، می‌توان مشاهده کرد که ۴۱۱۰ پیام در گروه «قطعا سالم» (Definitely ham) قرار می‌گیرند که از این میان، ۴۰۷۱ واقعا سالم هستند و تنها ۳۹ مورد اسپم بوده‌اند و به اشتباه دسته‌بندی شده‌اند. متقابلا، از میان ۲۳۳ پیامی که در گروه «قطعا هرزنامه» (definitely spam) قرار گرفته‌اند، تنها یک مورد واقعا سالم است و سایر آن‌ها هرزنامه هستند که این یعنی خوشه‌بندی به خوبی انجام شده است.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

البته، بیش از ۱۲۰۰ پیام در دسته ناشناخته (unknown) قرار گرفتند که این به نوبه خود رقم بالایی است. بنابراین، نیاز به انجام تحلیل‌های پیشرفته‌تری برای دسته‌بندی این پیام‌ها است. کاربر ممکن است از مواردی مانند «پردازش زبان طبیعی» (Natural Language Processing | NLP) برای کمک به بهبود صحت پیش‌بینی‌ها استفاده کند و در این راستا، می‌تواند از کتابخانه پایتون «کرس» (Keras) استفاده کند. در ادامه مطلب بهینه سازی در پایتون به روش استفاده از ماژول بهینه‌سازی در SciPy پرداخته شده است.

استفاده از ماژول بهینه‌سازی در SciPy

در این بخش از مطلب بهینه سازی با پایتون روش استفاده از ماژول بهینه‌سازی در SciPy مورد بررسی قرار گفته است. هنگامی که نیاز به بهینه‌سازی پارامترهای ورودی برای تابع است، scipy.optimize حاوی تعدادی متد کاربردی برای بهینه‌سازی انواع مختلفی از توابع است که در ادامه این بخش از مطلب بهینه سازی در پایتون به آن‌ها اشاره شده است.

فیلم آموزش بهینه سازی با کتابخانه SciPy در پایتون (رایگان) در فرادرس

کلیک کنید

متدهای minimize_scalar()‎ و minimize()‎ به ترتیب برای کمینه کردن توابع دارای یک یا تعداد زیادی متغیر مورد استفاده قرار می‌گیرند.
متد curve_fit()‎ برای برازش تابع روی یک مجموعه داده به کار می‌رود.
متدهای curve_fit()‎ و root()‎ به ترتیب برای پیدا کردن صفرهای توابع دارای یک و تعداد زیادی متغیر مورد استفاده قرار می‌گیرند.
linprog()‎ برای کمینه کردن یک تابع هدف خطی با محدودیت‌های نابرابری و برابری مورد استفاده قرار می‌گیرد.

بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

در عمل، همه این توابع کار بهینه‌سازی را انجام می‌دهند. در بخش بعدی از مطلب بهینه سازی در پایتون به دو تابع minimize_scalar()‎ و minimize()‎ پرداخته شده است. کد یکپارچه پروژه‌ای که در این بخش از مطلب بهینه سازی در پایتون بررسی شذ، در ادامه به طور کامل آمده است.

1"""
2Clustering example using an SMS spam dataset with SciPy.
3Associated with the Real Python article
4Scientific Python: Using SciPy for Optimization
5Available at: https://realpython.com/python-scipy-cluster-optimize/
6"""
7from pathlib import Path
8import numpy as np
9from scipy.cluster.vq import whiten, kmeans, vq
10
11HERE = Path(__file__).parent
12
13data = HERE.joinpath("SMSSpamCollection").read_text().strip().split("\n")
14
15digit_counts = np.empty((len(data), 2), dtype=int)
16for i, line in enumerate(data):
17    case, message = line.split("\t")
18    num_digits = sum(c.isdigit() for c in message)
19    digit_counts[i, 0] = 0 if case == "ham" else 1
20    digit_counts[i, 1] = num_digits
21
22unique_counts = np.unique(digit_counts[:, 1], return_counts=True)
23unique_counts = np.transpose(np.vstack(unique_counts))
24
25whitened_counts = whiten(unique_counts)
26codebook, _ = kmeans(whitened_counts, 3)
27codes, _ = vq(whitened_counts, codebook)
28
29ham_code = codes[0]
30spam_code = codes[-1]
31unknown_code = list(set(range(3)) ^ set((ham_code, spam_code)))[0]
32
33print("definitely ham:", unique_counts[codes == ham_code][-1])
34print("definitely spam:", unique_counts[codes == spam_code][-1])
35print("unknown:", unique_counts[codes == unknown_code][-1])
36
37digits = digit_counts[:, 1]
38predicted_hams = digits == 0
39predicted_spams = digits > 20
40predicted_unknowns = np.logical_and(digits > 0, digits <= 20)
41
42ham_cluster = digit_counts[predicted_hams]
43spam_cluster = digit_counts[predicted_spams]
44unknown_cluster = digit_counts[predicted_unknowns]
45
46print("hams:", np.unique(ham_cluster[:, 0], return_counts=True))
47print("spams:", np.unique(spam_cluster[:, 0], return_counts=True))
48print("unknowns:", np.unique(unknown_cluster[:, 0], return_counts=True))

چنانکه پیش‌تر نیز بیان شد، مجموعه داده مورد استفاده در مطلب بهینه سازی ریاضی در پایتون را می‌توان از این لینک [+] دانلود کرد. در بخش بعدی از مطلب بهینه سازی در پایتون به روش کمینه کردن یک تابع تک متغیره در SciPy پرداخته شده است.

کمینه کردن یک تابع تک متغیره در SciPy

در این بخش از مطلب بهینه سازی در پایتون روش کمینه کردن یک تابع تک متغیره در SciPy مورد بررسی قرار گرفته است. یک تابع ریاضیاتی که یک عدد را در ورودی می‌پذیرد و یک خروجی را ارائه می‌کند «تابع اسکالر» (Scalar Function) می‌گویند. این تابع، معمولا در تضاد با «توابع چند متغیره» (Multivariate Functions) است که چندین عدد را دریافت و نتیجه را نیز در چندین عدد خروجی باز می‌گرداند.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

مثالی از بهینه‌سازی توابع چند متغیره در بخش بعدی از مطلب بهینه سازی در پایتون ارائه شده است. در این بخش از مطلب بهینه سازی در پایتون به روش کمینه کردن یک تابع با یک متغیر در SciPy پرداخته شده است. در این بخش از مطلب بهینه سازی در پایتون تابع اسکالر یک تابع چند جمله‌ای درجه چهار و هدف، پیدا کردن مقدار کمینه تابع است. تابع، y = 3x⁴ - 2x + 1 است. تابع مذکور در تصویر زیر برای یک طیف از x از ۰ تا ۱ ترسیم شده است.

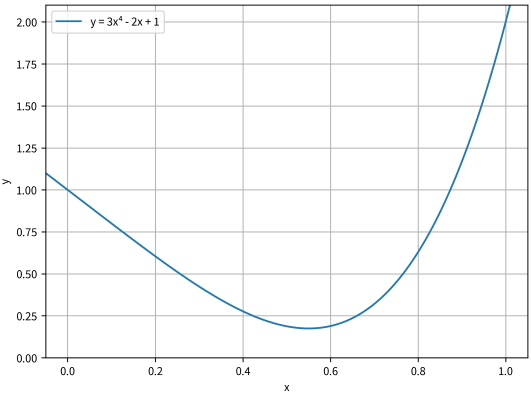
بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

در تصویر بالا، می‌توان مقدار کمینه این تابع را تقریبا در x = 0.55 مشاهده کرد. می‌توان از minimize_scalar()‎ برای تعیین مختصات x و y نقطه کمینه استفاده کرد. ابتدا، باید تابع minimize_scalar()‎ را از scipy.optimize وارد (ایمپورت | Import) کرد. سپس، نیاز به تعریف تابع هدف برای کمینه شدن است.

1from scipy.optimize import minimize_scalar
2
3def objective_function(x):
4    return 3 * x ** 4 - 2 * x + 1

تابع objective_function()‎ ورودی x را دریافت و عملیات ریاضی لازم را روی آن اعمال می‌کند؛ سپس، نتیجه را باز می‌گرداند. کاربر می‌تواند در تعریف تابع، از هر تابع ریاضیاتی که تمایل دارد استفاده کند. تنها محدودیتی که در این راستا وجود دارد، آن است که تابع باید یک عدد تنها را در پایان بازگرداند. سپس، از minimize_scalar()‎ برای پیدا کردن مقدار کمینه این تابع استفاده می‌شود. minimize_scalar()‎ تنها دارای یک ورودی لازم است که تعریف نام تابع هدف است.

1res = minimize_scalar(objective_function)

خروجی minimize_scalar()‎ یک نمونه از OptimizeResult است. این کلاس، بسیاری از جزئیات مرتبط را از اجرای بهینه‌ساز گردهم می‌آورد. این جزئیات، شامل موفق بودن یا نبودن بهینه‌ساز می‌شود. همچنین، در صورتی که بهینه‌ساز با موفقیت عمل کرده باشد، اینکه نتایج نهایی چه بوده‌اند را نیز گردآوری می‌کند. خروجی minimize_scalar()‎ برای این تابع، در زیر نمایش داده شده است.

     fun: 0.17451818777634331
    nfev: 16
     nit: 12
 success: True
       x: 0.5503212087491959

این نتایج، همه خصیصه‌های OptimizeResult هستند. success یک مقدار بولین است که نشان می‌دهد بهینه‌سازی با موفقیت کامل شده است یا خیر. اگر بهینه سازی با موفقیت کامل شده باشد، fun مقدار تابع هدف در نقطه بهینه x است. می‌توان از خروجی مشاهده کرد که بنابر آنچه انتظار می‌رفت، مقدار بهینه برای این تابع نزدیک به x = 0.55 است.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

نکته: همه توابع دارای کمینه نیستند. برای مثال، علاقه‌مندان می‌توانند تابع y = x³ را در این راستا بررسی کنند. برای minimize_scalar()‎، تابع هدف با هیچ مقدار کمینه‌ای معمولا منجر به یک خطای سرریز یعنی OverflowError می‌شود، زیرا بهینه‌ساز در نهایت عددی را امتحان می‌کند که برای انجام محاسبات توسط کامپیوتر، بسیار بزرگ است. برخلاف توابعی که هیچ مقدار کمینه‌ای ندارند، توابعی نیز وجود دارند که دارای چندین کمینه هستند. در این شرایط، minimize_scalar()‎ تضمین نمی‌کند که همه کمینه‌های سراسری تابع را پیدا کند. اگرچه، minimize_scalar()‎ دارای یک آرگومان کلیدواژه method است که می‌توان آن را برای کنترل حل کننده مسئله مورد استفاده برای بهینه‌سازی، تعیین کرد. کتابخانه پایتون سای‌پای (SciPy) دارای سه متد توکار برای کمینه‌سازی اسکالر است.

brent یک پیاده‌سازی از «الگوریتم برنت» (Brent’s Algorithm) است. این متد، پیش‌فرض است.
golden یک پیاده‌سازی از «جستجوی بخش طلایی» (Golden-Section Search) است. مستندات اشاره به این موضوع دارند که متد برنت معمولا بهتر است.
bounded پیاده‌سازی محدود از الگوریتم برنت است. این متد معمولا برای محدود کردن منطقه جستجو در هنگامی مفید است که کمینه در یک طیف مشخص قرار دارد.

هنگامی که method به صورت brent یا golden باشد، minimize_scalar()‎ آرگومان دیگری را می‌گیرد که به آن bracket گفته می‌شود. این، یک توالی از دو یا سه عنصر است که یک حدس اولیه را برای محدودیت‌های منطقه دارای مقدار کمینه فراهم می‌کند. اگرچه، این حلال‌ها تضمین نمی‌کنند که مقدار کمینه یافت شده در این طیف باشد.

از سوی دیگر، هنگامی که method به صورت bounded شد، minimize_scalar()‎ آرگومان دیگری را دریافت می‌کند که bounds نامیده می‌شود. این، یک توالی از دو عنصر است که منطقه جستجو برای کمینه را کاملا محدود می‌کنند. برای درک بهتر این مطلب، می‌توان متد bounded را همراه با تابع y = x⁴ - x² آزمود. این تابع، در تصویر زیر ترسیم شده است.

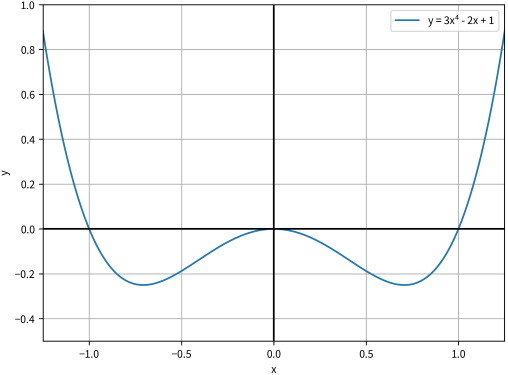
بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

با استفاده از کد نمونه پیشین، می‌توان objective_function()‎ را به صورت زیر بازتعریف کرد.

1def objective_function(x):
2    return x ** 4 - x ** 2

ابتدا، باید متد پیش‌فرض brent را آزمود.

1res = minimize_scalar(objective_function)

در این کد، مقداری برای method پاس داده نشده است؛ بنابراین، minimize_scalar()‎ از متد brent به صورت پیش‌فرض استفاده کرده است. خروجی این قطعه کد، به صورت زیر است.

     fun: -0.24999999999999994
    nfev: 15
     nit: 11
 success: True
       x: 0.7071067853059209

می‌توان مشاهده کرد که بهینه‌سازی موفقیت‌آمیز بوده است. کد بالا، مقدار بهینه را در نزدیکی x = 0.707 و y = -1/4 پیدا کرده است. اگر کاربر کمینه معادله را به طور تحلیلی به دست آورد، این مقدار را در x = 1/√2 پیدا می‌کند که بسیار نزدیک به پاسخ یافته شده توسط تابع پایتون است. اما اگر کاربر بخواهد که «کمینه متقارن» (Symmetric Minimum) را در x = -1/√2 پیدا کند، چه اقدامی باید انجام دهد؟ کاربر می‌تواند نتایج مشابهی را با فراهم کردن آرگومان براکت برای متد brent، بازگرداند.

1res = minimize_scalar(objective_function, bracket=(-1, 0))

در این کد، توالی (-1, 0)‎ برای bracket فراهم شد تا شروع به جستجو در منطقه بین ۱- و ۰ کند. کاربر انتظار دارد که کمینه در این منطقه قرار داشته باشد، زیرا تابع هدف حول محور y، متقارن است. اگرچه، حتی با bracket، متد brent همچنان کمینه را در x = +1/√2 باز می‌گرداند. برای پیدا کردن مقدار x = -1/√2، کاربر می‌تواند از متد bounded با bounds استفاده کند.

1res = minimize_scalar(objective_function, method='bounded', bounds=(-1, 0))

در این کد، method و bounds به عنوان آرگومان به minimize_scalar()‎ استفاده می‌شوند و bounds به گونه‌ای تنظیم می‌شود که از ۱- تا ۰ باشد. خروجی این متد به صورت زیر است.

   fun: -0.24999999999998732
 message: 'Solution found.'
    nfev: 10
  status: 0
 success: True
       x: -0.707106701474177

همانطور که انتظار می‌رفت، کمینه در x = -1/√2 یافت شد. خروجی افزوده از این متد شایان توجه است. این خروجی، حاوی خصیصه message در res است. این زمینه معمولا برای خروجی حاوی جزئیات بیشتر از برخی از حل کننده‌های مسائل کمینه‌سازی مورد استفاده قرار می‌گیرد.

فیلم آموزش بهینه سازی با پایتون – بررسی و حل مسائل تحقیق در عملیات در فرادرس

کلیک کنید

کد کامل پروژه کمینه کردن تابع اسکالر که در این بخش از مطلب بهینه سازی در پایتون مورد بررسی قرار گرفته در ادامه به صورت کامل آمده است. در بخش بعدی از مطلب بهینه سازی در پایتون به کمینه سازی تابع چندمتغیره در SciPy پرداخته شده است.

1"""
2Scalar function minimization example using SciPy.
3Associated with the Real Python article
4Scientific Python: Using SciPy for Optimization
5Available at: https://realpython.com/python-scipy-cluster-optimize/
6"""
7from scipy.optimize import minimize_scalar
8
9
10def objective_function(x):
11    return 3 * x ** 4 - 2 * x + 1
12
13
14res = minimize_scalar(objective_function)
15print(res)
16
17
18def objective_function(x):
19    return x ** 4 - x ** 2
20
21
22res = minimize_scalar(objective_function, method="brent")
23print(res)
24
25res = minimize_scalar(objective_function, method="bounded", bounds=[-1, 0])
26print(res)

کمینه‌سازی تابع چندمتغیره در SciPy

در این بخش از مطلب بهینه سازی در پایتون روش کمینه‌سازی تابع چندمتغیره در SciPy مورد بررسی قرار گرفته است. scipy.optimize شامل minimize()‎ عمومی‌تری نیز می‌شود. این تابع می‌تواند ورودی‌ها و خروجی‌های چند متغیره را مدیریت کند و دارای الگوریتم‌های بهینه‌سازی پیچیده‌تری است که قادر به مدیریت این موارد هستند. علاوه بر آن، minimize()‎ می‌تواند محدودیت‌های موجود روی راهکارهای مسأله را مدیریت کند.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

کاربر می‌تواند سه نوع قید محدودیت تعیین کند:

LinearConstraint: راه حل به وسیله گرفتن ضرب داخلی مقادیر X راه حل با آرایه ورودی کاربر و مقایسه نتایج با boundهای پایین‌تر و بالاتر، محدود شده است.
NonlinearConstraint: راه حل به وسیله اعمال یک تابع ارائه شده توسط کاربر برای مقادیر x تابع مخحدود می‌شود و مقدار بازگشت را با bound بالا و پایین مقایسه می‌کند.
Bounds: مقادیر راه حل x به قرار گرفتن بین کران بالا و پایین محدود شده است.

هنگامی که کاربر از این محدودیت‌ها استفاده می‌کند، می‌تواند انتخاب خاصی از متد بهینه‌سازی را که قادر به استفاده از آن است محدود کند، زیرا همه متدهای موجود از محدودیت‌ها بدین شکل پشتیبانی نمی‌کنند. اکنون، چگونگی استفاده از minimize()‎ در مثالی ارائه می‌شود. فرض می‌شود که کاربر یک کارگزار بورس است که علاقه‌مند به بیشینه کردن کل درآمد ناشی از فروش تعداد ثابتی از سهام‌های خود است. کاربر یک مجموعه مشخص از خریداران را تعیین می‌کند و برای هر خریدار، قیمتی که خریدار برای هر سهم می‌پردازد و اینکه چقدر پول نقد در دست دارد را می‌داند.

می‌توان این مسئله را به عنوان یک مسئله بهینه‌سازی محدود (Constrained Optimization Problem) تعبیر کرد. تابع هدف آن است که کاربر می‌خواهد درآمد خود را بیشینه کند. این در حالی است که minimize()‎ مقدار کمینه تابع را پیدا می‌کند؛ بنابراین، باید تابع هدف را در ۱- ضرب کرد تا مقادیر x که بزرگ‌ترین عدد منفی را تولید می‌کنند، پیدا شوند.

بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع

یک محدودیت روی مسئله وجود دارد. این محدودیت آن است که مجموع کل سهام‌های خریداری شده توسط خریداران از تعداد سهام‌هایی که کارگزار بورس در دسترس دارد نباید بیشتر باشد. همچنین، bound‌هایی روی هر یک از متغیرهای راهکار وجود دارد، زیرا هر خریدار دارای یک کران بالا از پول در دسترس و یک کران پایین صفر است. راهکار منفی x-values به معنای آن است که کارگزاری به خریداران پول می‌دهد.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

برای حل این مسئله که در این بخش از مطلب بهینه سازی در پایتون ارائه شده است، می‌توان از کد زیر استفاده کرد. ابتدا، ماژول‌هایی که کاربر نیاز دارد را باید وارد (ایمپورت) کند و سپس، یک مجموعه از متغیرها برای تعیین تعداد خریداران موجود در بازار و تعداد سهام‌هایی که کارگزار قصد فروش آن‌ها را دارد باید وارد شوند.

1import numpy as np
2from scipy.optimize import minimize, LinearConstraint
3
4n_buyers = 10
5n_shares = 15

در این کد، کاربر باید کتابخانه numpy و همچنین، توابع minimize()‎ و LinearConstraint را از scipy.optimize وارد کند. سپس، بازار ۱۰ خریدار که ۱۵ سهم را به طور کل از کاربر می‌خرند، تعیین می‌شود. سپس، باید آرایه‌هایی برای ذخیره‌سازی قیمت‌هایی که هر خریدار می‌پردازد، مقدار بیشینه‌ای که می‌توانند برای خرج کردن ارائه کنند و مقدار بیشینه سهم‌هایی که هر خریدار می‌توان ارائه کند ساخته شوند. در این مثال، می‌توان از تابع تولید عدد تصادفی در np.random برای تولید این آرایه‌ها استفاده کرد.

1np.random.seed(10)
2prices = np.random.random(n_buyers)
3money_available = np.random.randint(1, 4, n_buyers)

در قطعه کد بالا، دانه (Seed) برای مولد عدد تصادفی، توسط کاربر ارائه می‌شود. این تابع اطمینان حاصل می‌کند که کاربر با هر بار اجرای قطعه کد، مجموعه مشابهی از اعداد تصادفی را دریافت کند. در اینجا می‌توان اطمینان حاصل کرد که خروجی کاربر مشابه این مطلب راهنما است. هدف از این کار، فراهم کردن امکان مقایسه خروجی مخاطبان گرامی مطلب بهینه سازی در پایتون مجله فرادرس با آنچه محسوب می‌شود که در مطلب ارائه شده است.

در خط ۷، آرایه قیمت‌هایی که خریداران پرداخت می‌کنند به صورت pay. np.random.random()‎ می‌شود که یک آرایه از اعداد تصادفی روی بازه [0, 1)‏‎‎ است. تعداد عناصر موجود در آرایه به وسیله مقدار آرگومان تعیین می‌شود که در این موارد، تعداد خریداران است.
در خط ۸، آرایه‌ای از اعداد صحیح روی بازه ٰ[1, 4)‎ ساخته می‌شود؛ دوباره با تعداد خریداران. این آرایه، مقدار کل پول نقدی که هر خریدار در دسترس دارد را نشان می‌دهد. اکنون، کاربر نیاز به محاسبه بیشینه مقدار سهامی دارد که هر خریدار توانایی خرید آن را دارد.

1n_shares_per_buyer = money_available / prices
2print(prices, money_available, n_shares_per_buyer, sep="\n")

در خط ۹، کاربر نسبت money_available با prices را برای تعیین بیشینه تعداد سهامی که هر خریدار می‌تواند خریداری کند، محاسبه می‌کند. در نهایت، هر یک از این آرایه‌ها که با یک خط جدید از هم جدا شده‌اند، چاپ می‌شود. خروجی در زیر نمایش داده شده است.

[0.77132064 0.02075195 0.63364823 0.74880388 0.49850701 0.22479665
 0.19806286 0.76053071 0.16911084 0.08833981]
[1 1 1 3 1 3 3 2 1 1]
[ 1.29647768 48.18824404  1.57816269  4.00638948  2.00598984 13.34539487
 15.14670609  2.62974258  5.91328161 11.3199242 ]

سطر اول، آرایه قیمت‌ها است که اعداد اعشاری بین ۰ و ۱ هستند. این سطر، با بیشینه مقدار نقدی که در اعداد صحیح از ۱ تا ۴ موجود است، دنبال می‌شوند. در نهایت، تعداد سهم‌هایی که هر خریدار توانایی خرید آن را دارد، مشاهده می‌شوند.

فیلم آموزش کتابخانه SciPy برای محاسبات علمی در پایتون – بخش یکم در فرادرس

کلیک کنید

اکنون، کاربر نیاز به ساخت constraints و bounds برای حلال دارد. این محدودیت، مجموع سهام‌های خریداری شده است که نمی‌تواند از تعداد کل سهام‌های در دسترس (که کارگزار بورس می‌فروشد) بیشتر باشد. این بیشتر یک محدودیت است تا یک قید؛ زیرا شامل بیش از یک راهکار موجود می‌شود.

برای ارائه آنچه بیان شد به صورت ریاضیاتی، می‌توان گفت که x[0] + x[1] + ... + x[n] = n_shares‎، که در آن، n تعداد کل خریداران است. به طور خلاصه، کاربر می‌توان ضرب داخلی برداری با مقادیر راه حل را دریافت کند و آن را محدود به مساوی بودن با n_shares کند. باید به خاطر داشت که LinearConstraint ضرب داخلی آرایه ورودی با مقادیر راه حل را دریافت و آن‌ها را با کران بالا و پایین مقایسه می‌کند. می‌توان از قطعه کد زیر برای تنظیم محدودیت روی n_shares استفاده کرد.

1constraint = LinearConstraint(np.ones(n_buyers), lb=n_shares, ub=n_shares)

در قطعه کد بالا، یک آرایه با طول n_buyers ساخته می‌شود و سپس، این آرایه به عنوان اولین آرگومان به LinearConstraint پاس داده می‌شود. با توجه به اینکه LinearConstraint ضرب داخلی بردار راه حل با این آرگومان بیان شده را دریافت می‌کند، در نتیجه مجموع سهام‌های خریداری شده را ارائه می‌کند. این نتیجه، به گونه‌ای محدود شده است که بین دو آرگومان دیگر قرار بگیرد. این آرگومان‌ها، در ادامه بیان شده‌اند.

کران پایین lb
کران بالای ub

از آنجا که lb = ub = n_shares، این یک محدودیت برابر است، زیرا مجموع مقادیر باید مساوی با هر دو lb و ub باشد. اگر lb از ub متفاوت باشد، یک محدودیت نابرابری خواهد بود. سپس، قیود برای متغیر راهکار ساخته می‌شوند. قیود، تعداد سهام‌های خریداری شده را محدود به ۰ در سمت پایین‌تر و n_shares_per_buyer در سمت بالاتر می‌کنند. قالبی که minimize()‎ برای قیود انتظار دارد، یک توالی از تاپل‌ها از قیود پایین‌تر و بالاتر است.

1bounds = [(0, n) for n in n_shares_per_buyer]

در این کد، از comprehension برای تولید یک لیست از تاپل‌ها برای هر خریدار استفاده شده است. آخرین گام پیش از آنکه بهینه‌سازی اجرا شود، تعریف تابع هدف است. باید به خاطر داشت که کارگزاری تلاش می‌کند تا درآمد خود را بیشینه کند. به طور هم‌ارز، کارگزار می‌خواهد که منفی درآمد خود را تا حد ممکن، بزرگ کند.

فیلم آموزش بهینه سازی با پایتون – بررسی و حل مسائل تحقیق در عملیات در فرادرس

کلیک کنید

درآمدی که از هر فروش تولید می‌شود، قیمتی است که خریدار می‌پردازد و با عدد سهام‌هایی که خریداری شده است ضرب می‌شود. به بیان ریاضی، می‌توان این مورد را به صورت prices[0]*x[0] + prices[1]*x[1] + ... + prices[n]*x[n]‎ نوشت که در آن، N تعداد کل خریداران است. یک بار دیگر، این مورد را به طور خلاصه‌تر می‌توان با ضرب داخلی یا x.dot(prices)‎ نمایش داد. این یعنی تابع هدف باید x مقادیر راه حل کنونی و آرایه قیمت‌ها به عنوان آرگومان را دریافت کند.

1def objective_function(x, prices):
2    return -x.dot(prices)

در این کد، کاربر تابع objective_function()‎ را برای گرفتن دو آرگومان تعریف می‌کند. سپس، ضرب داخلی x با قیمت‌ها را دریافت و مقدار منفی آن مقدار را باز می‌گرداند. باید به خاطر داشت که باید مقدار منفی بازگردانده شود. زیرا هدف آن است که مقدار را تا حد ممکن کوچک و یا به منفی بی‌نهایت نزدیک کرد. در نهایت، می‌توان تابع minimize()‎ را فراخوانی کرد.

1res = minimize(
2    objective_function,
3    x0=10 * np.random.random(n_buyers),
4    args=(prices,),
5    constraints=constraint,
6    bounds=bounds,
7)

در این قطعه کد، res نمونه‌ای از OptimizeResult است؛ درست مانند minimize_scalar()‎. همانطور که می‌تواند مشاهده کرد، تعداد زیادی از فیلدهای مشابه وجود دارند، حتی با وجود آنکه مسئله کاملا متفاوت است. در فراخوانی برای minimize()‎، پنج آرگومان پاس داده می‌شوند.

objective_function: اولین آرگومان موقعیتی، باید تابعی باشد که کاربر بهینه می‌کند.
x0: دومین آرگومان، حدس اولیه برای مقادیر راه حل است. در این مثال، یک آرایه تصادفی از مقادیر بین ۰ و ۱۰ فراهم می‌شود که طول آن n_buyer است. برای برخی از الگوریتم‌ها یا مسائل، انتخاب یک حدس اولیه مناسب کار بسیار مهمی است. اگرچه، در این مثال، این حدس اولیه به نظر خیلی مهم نمی‌رسد.
args: آرگومان بعدی، یک تاپل از دیگر آرگومان‌ها است که برای پاس داده شدن به تابع هدف، حیاتی محسوب می‌شود. minimize()‎ همیشه مقدار کنونی راه حل x را به تابع هدف پاس می‌دهد؛ بنابراین این آرگومان مانند موقعیتی برای نگهداری هر ورودی لازم عمل می‌کند. در این مثال، کاربر نیاز دارد که prices را به objective_function()‎ پاس دهد تا به آنجا برود.
constraints: آرگومان بعدی یک توالی از محدودیت‌ها روی مسئله است. کاربر محدودیت‌هایی که پیش‌تر تولید شده است را روی تعدادی از سهام‌های موجود، پاس می‌دهد.
bounds: آخرین آرگومان، توالی قیود روی متغیرهای راه حلی محسوب می‌شود که کاربر پیش‌تر تولید کرده است.

هنگامی که حل کننده مسئله اجرا می‌شود، باید آن را با استفاده از res وارسی کرد.

     fun: -8.783020157087478
     jac: array([-0.7713207 , -0.02075195, -0.63364828, -0.74880385, 
       -0.49850702, -0.22479665, -0.1980629 , -0.76053071, -0.16911089,
       -0.08833981])
 message: 'Optimization terminated successfully.'
    nfev: 204
     nit: 17
    njev: 17
  status: 0
 success: True
       x: array([1.29647768e+00, 2.78286565e-13, 1.57816269e+00,
       4.00638948e+00, 2.00598984e+00, 3.48323773e+00, 3.19744231e-14,
       2.62974258e+00, 2.38121197e-14, 8.84962214e-14])

در این خروجی، می‌توان message و status را مشاهده کرد که حالت نهایی بهینه‌سازی را نمایش می‌دهند. برای این بهینه‌ساز، وضعیت صفر (۰) به معنی آن است که بهینه‌سازی با موفقیت به پایان رسیده است، که می‌توان آن را در message مشاهده کرد. با توجه به آنکه بهینه‌سازی موفقیت‌آمیز بوده است، fun مقدار تابع هدف در مقادیر راه حل بهینه را نشان می‌دهد. در واقع، کارگزار $8.78‎ درآمد از این فروش دارد.

فیلم آموزش مقدماتی پیاده سازی مسائل بهینه سازی در پایتون Python در فرادرس

کلیک کنید

می‌توان مقادیر x که تابع را بهینه می‌کنند در res مشاهده کرد. در این مورد، نتیجه آن است که کارگزاری باید در حدود ۱٫۳ سهام خود را به اولین خریدار، هیچ مقدار به دومین خریدار، ۱٫۶ را به سومین خریدار، ۴٫۰ را به چهارمین خریدار و به همین ترتیب، بدهد. کاربر باید بررسی و اطمینان حاصل کند که محدودیت‌ها و قیودی که تعیین کرده، ارضا شده‌اند. می‌توان این کار را با استفاده از کد زیر انجام داد.

1print("The total number of shares is:", sum(res.x))
2print("Leftover money for each buyer:" money_available - res.x * prices)

در این کد، کاربر مجموع سهم‌های خریداری شده توسط هر خریدار را چاپ می‌کند که مساوی با n_shares است. سپس، کاربر تفاوت بین پول نقد در دسترس هر خریدار و میزانی که هزینه می‌کند را چاپ می‌کند. هر یک از این مقادیر باید مثبت باشند. خروجی این موارد در ادامه نمایش داده شده‌اند.

The total number of shares is: 15.000000000000002
Leftover money for each buyer: [3.08642001e-14 1.00000000e+00 
 3.09752224e-14 6.48370246e-14 3.28626015e-14 2.21697984e+00
 3.00000000e+00 6.46149800e-14 1.00000000e+00 1.00000000e+00]

همانطور که مشهود است، همه محدودیت‌ها و قیود روی مسئله ارضا شده‌اند. اکنون، باید تلاش شود تا مسئله تغییر کند، در غین این صورت حل کننده مسئله (Solver) نمی‌تواند راهکار را پیدا کند. باید n_shares را به مقدار 1000 تغییر داد تا بتوان ۱۰۰۰ سهم را به خریداران مشابهی اراسه کرد. هنگامی که فرد تابع minimize()‎ را اجرا کند، می‌تواند نتایج را به صورت زیر مشاهده کرد.

     fun: nan
     jac: array([nan, nan, nan, nan, nan, nan, nan, nan, nan, nan])
 message: 'Iteration limit exceeded'
    nfev: 2182
     nit: 101
    njev: 100
  status: 9
 success: False
       x: array([nan, nan, nan, nan, nan, nan, nan, nan, nan, nan])

شایان توجه است که خصیصه status اکنون دارای مقدار ۹ است و message حاکی از آن است که محدودیت تکرار سرریز کرده است. هیچ راهی برای فروش ۱۰۰۰ سهم با مقدار پول داده شده توسط هر خریدار و تعداد خریداران حاضر در بازار وجود ندارد. اگرچه، به جای ایجاد خطا، minimize()‎ همچنان یک نمونه OptimizeResult را باز می‌گرداند. کاربر نیاز به حصول اطمینان از آن دارد که وضعیت کد را پیش از اقدام با محاسبات بعدی، بررسی کند. کد یکپارچه پروژه مثال ارائه شده در این بخش از مطلب بهینه سازی در پایتون در ادامه به طور کامل آمده است.

1"""
2Constrained minimization example code using SciPy.
3Associated with the Real Python article
4Scientific Python: Using SciPy for Optimization
5Available at: https://realpython.com/python-scipy-cluster-optimize/
6"""
7import numpy as np
8from scipy.optimize import minimize, LinearConstraint
9
10n_buyers = 10
11n_shares = 15
12np.random.seed(10)
13prices = np.random.random(n_buyers)
14money_available = np.random.randint(1, 4, n_buyers)
15n_shares_per_buyer = money_available / prices
16print(prices, money_available, n_shares_per_buyer, sep="\n")
17constraint = LinearConstraint(np.ones(n_buyers), lb=n_shares, ub=n_shares)
18bounds = [(0, n) for n in n_shares_per_buyer]
19
20
21def objective_function(x, prices):
22    return -x.dot(prices)
23
24
25res = minimize(
26    objective_function,
27    10 * np.random.random(n_buyers),
28    args=(prices,),
29    constraints=constraint,
30    bounds=bounds,
31)
32print(res)
33
34print("The total number of shares is:", sum(res.x))
35print("Leftover money for each buyer:", money_available - res.x * prices)

جمع‌بندی

در مطلب بهینه سازی در پایتون اکوسیستم «سای‌پای» (SciPy) و تفاوت آن با کتابخانه پایتون سای‌پای مورد بررسی قرار گرفت. همچنین، برخی از ماژول‌های موجود در سای‌پای بیان و روش نصب SciPy با استفاده از توزیع پایتون آناکوندا (مدیر بسته کوندا) و همچنین pip، در ادامه مطلب بهینه سازی در پایتون آموزش داده شد. سپس، مثال‌هایی تشریح شدند که در آن‌ها از عملکردهای خوشه‌بندی و بهینه‌سازی در سای‌پای استفاده شده بود.

فیلم مجموعه آموزش الگوریتم های بهینه سازی هوشمند – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

در مثال مربوط به خوشه‌بندی که در مطلب بهینه سازی با پایتون ارائه شد، الگوریتمی برای مرتب‌سازی پیام‌های اسپم از پیام‌های سالم، توسعه داده شد. با استفاده از kmeans()‎، کشف شد که احتمال اسپم بودن پیام‌هایی با بیش از ۲۰ رقم نوشته شده در آن‌ها، فوق‌العاده زیاد است. در مثال بهینه‌سازی، ابتدا مقدار کمینه در یک تابع ریاضیاتی شفاف با تنها یک متغیر بررسی شد.

سپس، مثال پیچیده‌تری پیرامون بیشینه‌سازی سود سبد سهام در ادامه مطلب بهینه سازی با پایتون مورد بررسی قرار گرفت. با استفاده از minimize()‎، تعداد بهینه سهام‌هایی که باید به گروهی از خریداران فروخته شود تشریح شد. سای‌پای یک کتابخانه بسیار بزرگ با ماژول‌ها بسیار زیاد است. با دانش کسب شده از مطلب بهینه سازی در پایتون کاربران می‌توانند شروع به اکتشاف در حوزه بهینه‌سازی با پایتون کنند. برای مطالعه بیشتر پیرامون بهینه‌سازی ریاضیاتی و الگورتیم‌های گوناگون موجود برای آن مطالعه مطلب «روش های بهینه سازی در یادگیری ماشین — راهنمای کاربردی» اکیدا توصیه می‌شود.

بر اساس رای ۳ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

Real Python

الهام حصارکی (+)

«الهام حصارکی»، فارغ‌التحصیل مقطع کارشناسی ارشد مهندسی فناوری اطلاعات، گرایش سیستم‌های اطلاعات مدیریت است. او در زمینه هوش مصنوعی و داده‌کاوی، به ویژه تحلیل شبکه‌های اجتماعی، فعالیت می‌کند.

۲ دیدگاه برای «بهینه سازی در پایتون | Optimization در پایتون با SciPy | راهنمای جامع»

سیدمصطفی

۱۴ خرداد، در ۱۴۰۲ ۱:۵۸ ب.ظ

با سلام و تشکر بابت آموزش جامع ارائه شده، در قسمت محاسبه codes کد احتمالا بصورت اشتباه تایپ شده است و کد صحیح به صورت زیر می باشد:
codes, _ = vq(whitened_counts, codebook)

پاسخ