برنامه محاسبه e به توان عدد x – راهنمای کاربردی
در این مطلب، برنامه محاسبه e به توان عدد x ارائه شده است. محاسبه مقدار تابع نمایی ex با استفاده از «سری تیلور» (Taylor Series)، به صورت زیر، امکانپذیر است.
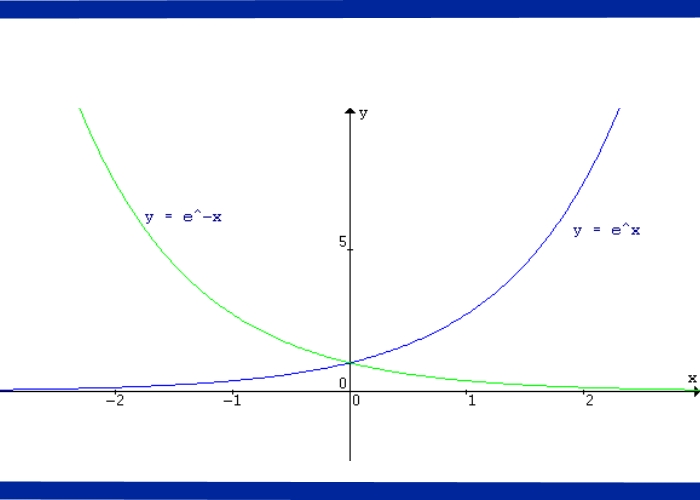
e^x = 1 + x/1! + x^2/2! + x^3/3! + ......
پرسشی که اکنون مطرح میشود این است که چگونه میتوان به صورت کارا، مجموع سری بالا را محاسبه کرد. سری را میتوان به صورت زیر نوشت:
e^x = 1 + (x/1) (1 + (x/2) (1 + (x/3) (........) ) )
مجموعی که نیاز به محاسبه آن برای n عبارت وجود دارد را میتوان با استفاده از حلقهای که در زیر آمده، محاسبه کرد.
for (i = n - 1, sum = 1; i > 0; --i ) sum = 1 + x * sum / i;
در ادامه، پیادهسازی راهکار بالا در زبانهای برنامهنویسی ++C/C، «جاوا» (Java)، «پایتون ۳» (Python 3)، «سیشارپ» (#C) و «پیاچپی» (PHP) انجام شده است. برای آشنایی بیشتر با عدد e، مطالعه مطلب «توابع نمایی و عدد e — به زبان ساده» و همچنین، برای آشنایی بیشتر با سری تیلور، مطالعه مطلب «سری تیلور — از صفر تا صد» توصیه میشود.
برنامه محاسبه e به توان عدد x در ++C/C
برنامه محاسبه e به توان عدد x در جاوا
برنامه محاسبه e به توان عدد x در پایتون ۳
برنامه محاسبه e به توان عدد x در سی شارپ
برنامه محاسبه e به توان عدد x در PHP
خروجی
همانطور که مشهود است، در قطعه کدهای بالا (همه کدهای ارائه شده برای زبانهای گوناگون شامل پایتون، جاوا، ++C و سیشارپ)، مقدار x برابر با ۱ وارد شده است.
در نتیجه، خروجی قطعه کدهای بالا به ازای x=1، برابر با مقدار ارائه شده در زیر است.
e^x = 2.718282
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش برنامهنویسی C++
- مجموعه آموزشهای ریاضیات
- یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
- الگوریتم بازی مار و پله همراه با کد — به زبان ساده
- حل مساله n وزیر با الگوریتم پسگرد (Backtracking) — به زبان ساده
^^













سلام
eبه توان( ۱-)چن میشه؟