مشتق گیری عددی — به زبان ساده

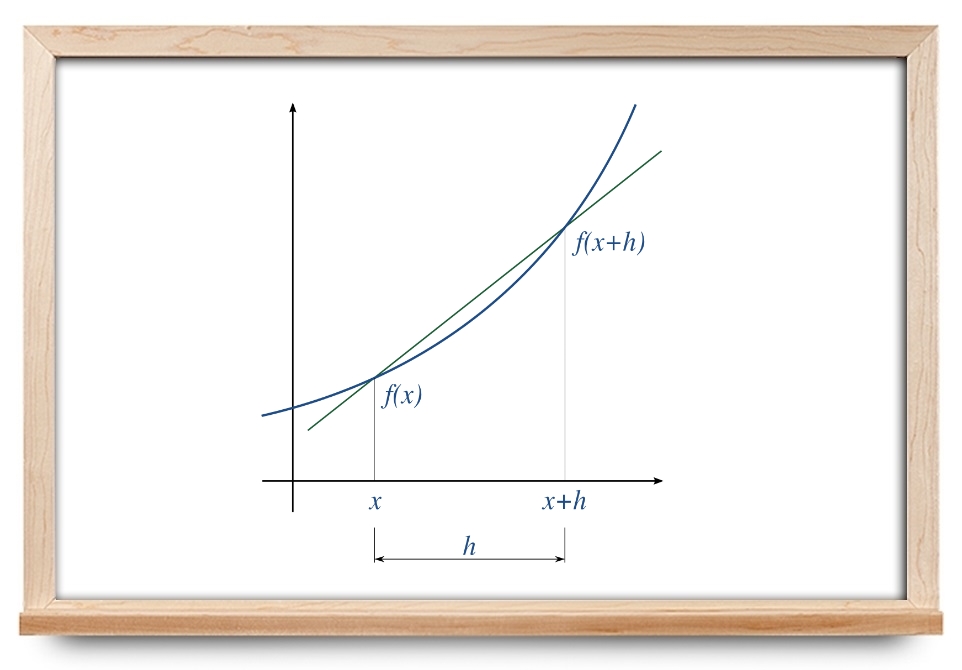
در آموزش‌های قبلی مجله فرادرس، درباره مشتق و روش‌های مشتق‌گیری بحث کردیم. در این آموزش، فرمول‌های مشتق گیری عددی را معرفی می‌کنیم. این فرمول‌ها، تفاضل رو به جلو، تفاضل رو به عقب و تفاضل مرکزی هستند. پیاده‌سازی این فرمول‌ها در پایتون نیز ارائه شده است.

تعریف مشتق

مشتق تابع $$f (x )$$ در نقطه $$x = a$$ با حد زیر محاسبه می‌شود:

$$\large f ^ \prime ( a ) = \lim _ { h \to 0 } \frac { f ( a + h ) - f ( a ) } { h }$$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

فرمول‌های تفاضل

سه فرمول اصلی برای مشتق‌گیری تقریبی عددی وجود دارد:

۱) فرمول تفاضل رو به جلو (Forward Difference Formula) با اندازه گام $$h$$:

$$\large f ^ \prime ( a ) \approx \frac { f ( a + h ) - f ( a ) } { h }$$

۲) فرمول تفاضل رو به عقب (Backward Difference Formula) با اندازه گام $$h$$:

$$\large f ^ \prime ( a ) \approx \frac { f ( a ) - f ( a - h ) } { h }$$

۳) فرمول تفاضل مرکزی (Central Difference Formula) با اندازه گام $$h$$، میانگین فرمول‌های تفاضل رو به جلو و تفاضل رو به عقب است:

$$\large \begin {align*} f ^ \prime ( a ) & \approx \frac { 1 } { 2 } \left ( \frac { f ( a + h ) - f ( a ) } { h } + \frac { f ( a ) - f ( a - h ) } { h } \right ) \\ & = \frac { f ( a + h ) - f ( a - h ) } { 2 h } \end {align*}$$

پیاده‌سازی مشتق گیری عددی در پایتون

ابتدا کتابخانه‌های لازم را فراخوانی می‌کنیم:

1import numpy as np
2import matplotlib.pyplot as plt
3%matplotlib inline
4            <div class="faradars-courses faradars-courses-single">
5                <a href="https://faradars.org/courses/fvpht99021-supplementary-of-python-first-part?utm_source=blog.faradars&utm_medium=referral-post&utm_campaign=related-courses-inline-5&utm_term=s.hamidi&utm_content=mathematics" target="_blank">
6                    <div class="card card-course">
7                        <div class="card-image">
8                            <img class="pop-img" src="https://faradars.org/wp-content/uploads/2020/05/fvpht99021-svg.svg" alt="آموزش برنامه نویسی پایتون Python – تکمیلی – بخش یکم">
9                        </div>
10                        <div class="card-body">
11                            <div class="card-title">
12                                فیلم آموزش برنامه نویسی پایتون Python – تکمیلی – بخش یکم در فرادرس
13                            </div>
14                        </div>
15                        <div class="card-action ml-3">
16                            <div class="fdb-btn">کلیک کنید</div>
17                        </div>
18                    </div>
19                </a>
20            </div>
21        

برای پیاده‌سازی فرمول‌های مشتق‌‌گیری عددی در پایتون، تابعی به نام derivative را می‌نویسیم که ورودی‌های آن method ،a ،f و h هستند (با مقادیر پیش‌فرض 'method='central و h=0.01). خروجی تابع مورد نظر، متناظر با خروجی فرمول تفاضل برای $$f'(a)$$ با اندازه گام $$h$$ است.

1def derivative(f,a,method='central',h=0.01):
2    '''Compute the difference formula for f'(a) with step size h.
3
4    Parameters
5    ----------
6    f : function
7        Vectorized function of one variable
8    a : number
9        Compute derivative at x = a
10    method : string
11        Difference formula: 'forward', 'backward' or 'central'
12    h : number
13        Step size in difference formula
14
15    Returns
16    -------
17    float
18        Difference formula:
19            central: f(a+h) - f(a-h))/2h
20            forward: f(a+h) - f(a))/h
21            backward: f(a) - f(a-h))/h            
22    '''
23    if method == 'central':
24        return (f(a + h) - f(a - h))/(2*h)
25    elif method == 'forward':
26        return (f(a + h) - f(a))/h
27    elif method == 'backward':
28        return (f(a) - f(a - h))/h
29    else:
30        raise ValueError("Method must be 'central', 'forward' or 'backward'.")

برنامه بالا را برای چند تابع ساده بررسی می‌کنیم. به عنوان مثال، برای تابع کسینوس، داریم:

$$\large \left . \frac { d } { d x } \left ( \cos x \right ) \, \right | _ { x = 0 } = - \sin ( 0 ) = 0$$

اگر از تابع پایتون زیر نیز استفاده کنیم، خروجی صفر را خواهد داد:

1derivative(np.cos,0)

خروجی:

10.0

برای روش رو به جلو نیز داریم:

1derivative(np.cos,0,method='forward',h=1e-8)

خروجی:

10.0

به عنوان مثالی دیگر، برای تابع نمایی نیز می‌دانیم:

$$\large \left . \frac { d } { d x } \left ( e ^ x \right) \, \right | _ { x = 0 } = e ^ 0 = 1$$

با استفاده از تابع پایتون نیز داریم:‌

1derivative(np.exp,0,h=0.0001)

خروجی:

11.0000000016668897

اگر بخواهیم از روش رو به عقب استفاده کنیم، دستور زیر را می‌نویسیم:

1derivative(np.exp,0,method='backward',h=0.0001)

خروجی:

10.9999500016666385

تابعی که نوشتیم، آرایه‌ای از ورودی‌ها را برای $$a$$ می‌گیرد و مقدار مشتق را برای آن مقدار $$a$$ محاسبه و به عنوان خروجی ارائه می‌کند. برای مثال، مشتق $$\sin (x)$$ را می‌توانیم به صورت زیر رسم کنیم:

1x = np.linspace(0,5*np.pi,100)
2dydx = derivative(np.sin,x)
3
4dYdx = np.cos(x)
5
6plt.figure(figsize=(12,5))
7plt.plot(x,dydx,'r.',label='Central Difference')
8plt.plot(x,dYdx,'b',label='True Value')
9
10plt.title('Central Difference Derivative of y = cos(x)')
11plt.legend(loc='best')
12plt.show()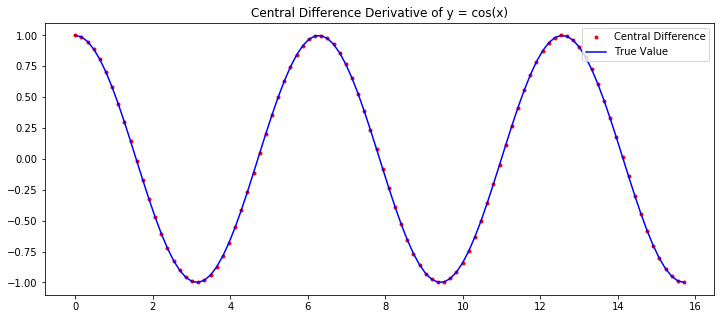

اکنون می‌خواهیم مشتق تابع نسبتاً پیچیده زیر را محاسبه و رسم کنیم:‌

$$\large y = \left ( \frac { 4 x ^ 2 + 2 x + 1 } { x + 2 e ^ x } \right ) ^ x$$

1x = np.linspace(0,6,100)
2f = lambda x: ((4*x**2 + 2*x + 1)/(x + 2*np.exp(x)))**x
3y = f(x)
4dydx = derivative(f,x)
5
6plt.figure(figsize=(12,5))
7plt.plot(x,y,label='y=f(x)')
8plt.plot(x,dydx,label="Central Difference y=f'(x)")
9plt.legend()
10plt.grid(True)
11
12plt.show()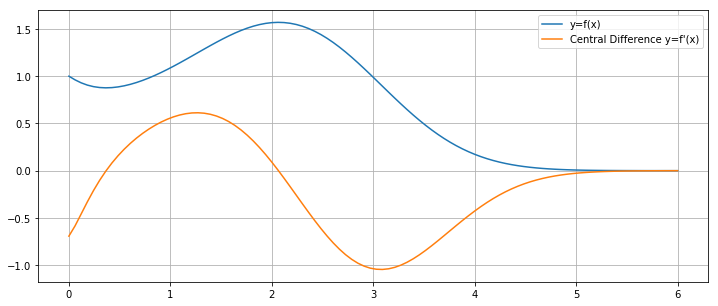

فرمول‌های خطا

پرسشی که هنگام تقریب زدن پیش می‌آید، این است که دقت مناسب فرمول‌های تفاضل رو به جلو، رو به عقب و مرکزی چقدر است؟ به همین دلیل، فرمول‌های خطا را با استفاده از سری تیلور پیدا می‌کنیم.

فیلم آموزش محاسبات عددی در پایتون Python در فرادرس

کلیک کنید

قضیه

چندجمله‌ای تیلور مرتبه $$n$$ تابع $$f (x )$$ در $$x = a$$ با جمله باقیمانده به صورت زیر است:

$$\large \begin {align*} f ( x ) & = f ( a ) + f ^ \prime ( a ) ( x - a ) + \frac { f ^ {\prime \prime } ( a ) } { 2 } ( x - a ) ^ 2 \\ & \, \, \, \, \, \, \, \, + \cdots + \frac { f ^ { ( n ) } ( a ) } { n ! } ( x - a ) ^ n + \frac { f ^ { ( n + 1 ) } ( c ) } { ( n + 1 ) ! } ( x - a ) ^ { n + 1 } \end {align*}$$

که در آن، $$c$$ مقداری بین $$x$$ و $$a$$ است.

قضیه

خطای فرمول تفاضل رو به جلو برابر است با:

$$\large \left | \, \frac { f ( a + h ) - f ( a ) } { h } - f ^ \prime ( a ) \, \right | \leq \frac { h K _ 2 } { 2 }$$

که در آن، برای همه $$x \in [a,a+h]$$ رابطه $$\left| \, f ^ {\prime \prime }(x) \, \right| \leq K_2$$ برقرار است. فرمول خطای مشابهی برای روش تفاضل رو به عقب برقرار است.

اثبات: فرمول تیلور مرتبه اول را در نظر بگیرید:

$$\large f ( x ) = f ( a ) + f ^ \prime ( a ) ( x - a ) + \frac { f ^ { \prime \prime } ( c ) } { 2 } ( x - a ) ^ { 2 }$$

با فرض $$x = a+h$$ و جایگذاری آن در فرمول بالا، داریم:

$$\large \begin {align} f ( a + h ) & = f ( a ) + f ^ \prime ( a ) h + \frac { f ^ { \prime \prime } ( c ) } { 2 } h ^ { 2 } \\ f ( a + h ) - f ( a ) & = f ^ \prime ( a ) h + \frac { f ^ {\prime \prime } ( c ) } { 2 } h ^ { 2 } \\ \frac { f ( a + h ) - f ( a ) } { h } & = f ^ \prime ( a ) + \frac { f ^ {\prime \prime } ( c ) } { 2 } h \\ \frac { f ( a + h ) - f ( a ) } { h } - f ^ \prime ( a ) & = \frac { f ^ { \prime \prime } ( c ) } { 2 } h \\ \end{align}$$

$$K_2$$ را به گونه‌ای در نظر بگیرید که برای همه $$x \in [a,a+h]$$، رابطه $$| f ^ { \prime \prime } ( x ) | \leq K _ 2$$ برقرار باشد.

قضیه

خطای فرمول تفاضل مرکزی، برابر است با:

$$\large \left | \frac { f ( a + h ) - f ( a - h ) } { 2 h } - f' ( a ) \right | \leq \frac { h ^ 2 K _ 3 } { 6 }$$

که در آن، برای همه $$x \in [a-h,a+h]$$، رابطه $$| f ^ { \prime \prime \prime } ( x ) | \leq K _ 3$$ برقرار است.

اثبات: چندجمله‌ای مرتبه دوم تیلور را در نظر بگیرید:

$$\large f ( x ) = f ( a ) + f' ( a ) ( x - a ) + \frac { f ^ { \prime \prime } ( a ) } { 2 } ( x - a ) ^ 2 + \frac { f ^ {\prime \prime \prime } ( c ) } { 6 } ( x - a ) ^ { 3 }$$

تساوی‌های $$x = a + h$$ و $$x = a - h$$ را در نظر بگیرید. روابط زیر را داریم:

$$\large \begin {align} f ( a + h ) & = f ( a ) + f ^ \prime ( a ) h + \frac { f ^ {\prime \prime } ( a ) } { 2 } h ^ 2 + \frac { f ^ { \prime \prime \prime } ( c _ 1 ) } { 6 } h ^ { 3 } \\ f ( a - h ) & = f ( a ) - f ^ \prime ( a ) h + \frac { f ^ {\prime \prime } ( a ) } { 2 } h ^ 2 - \frac { f ^ { \prime \prime \prime } ( c _ 2 ) } { 6 } h ^ { 3 } \\ f ( a + h ) - f ( a - h ) & = 2 f ^ \prime ( a ) h + \frac { f ^ { \prime \prime \prime } ( c _ 1 ) } { 6 } h ^ { 3 } + \frac { f ^ { \prime \prime \prime } ( c _ 2 ) } { 6 } h ^ { 3 } \\ \frac { f ( a + h ) - f ( a - h ) } { 2 h } - f ^ \prime ( a) & = \frac { f ^ {\prime \prime \prime } ( c _ 1 ) + f ^ {\prime \prime \prime } ( c _ 2 ) } { 1 2 } h ^ { 2 } \\ \end{align}$$

توجه کنید که $$f ^ { \prime \prime \prime } ( x )$$ پیوسته است (طبق فرض) و $$( f ^ { \prime \prime \prime } ( c _ 1 ) + f ^ { \prime \prime \prime } ( c _ 2 ) ) / 2$$ بین $$f ^ { \prime \prime \prime } ( c _ 1 )$$ و $$f ^ { \prime \prime \prime } ( c _ 2 )$$ قرار دارد. بنابراین، طبق قضیه مقدار میانی، یک $$c$$ بین $$c _ 1$$ و $$c _ 2$$ به گونه‌ای وجود دارد که رابطه زیر برقرار باشد:

$$\large f ^ { \prime \prime \prime } ( c ) = \frac { f ^ { \prime \prime \prime } ( c _ 1 ) + f ^ { \prime \prime \prime } ( c _ 2 ) } { 2 }$$

$$K_3$$ به گونه‌ای است که برای همه $$x \in [a-h,a+h]$$ رابطه $$\left | \, f ^ { \prime \prime \prime } ( x ) \, \right | \leq K _ 3$$ برقرار باشد.

مثال‌

در این مثال می‌خواهیم چندجمله‌ای تیلور مرتبه سوم $$T_3(x)$$ تابع $$f(x) = \frac{3e^x}{x^2 + x + 1}$$ را با مرکز $$x = 0$$ و در بازه $$x \in [-3,3]$$ رسم کنیم. ابتدا نمودار $$y = f (x )$$ را رسم می‌کنیم:

1x = np.linspace(-3,3,100)
2f = lambda x: 3*np.exp(x) / (x**2 + x + 1)
3y = f(x)
4plt.plot(x,y);
5plt.show()

اکنون ضرایب $$a_n = \frac{f^{(n)}(0)}{n!}$$ را برای $$n=0,1,2,3$$ محاسبه می‌کنیم:

1a0 = f(0)
2a1 = derivative(f,0,dx=0.001,n=1)
3a2 = derivative(f,0,dx=0.001,n=2) / 2
4a3 = derivative(f,0,dx=0.001,n=3,order=5) / 6
5# The parameter order specifies the number of points to use
6# The value order must be odd and at least n + 1
7
8print(a0,a1,a2,a3)

خروجی:

13.0 1.99999838912e-06 -1.50000037502 1.99999209786

در نهایت، $$f (x )$$ و $$T_3 (x )$$ را با هم در یک شکل رسم می‌کنیم:

1T3 = a0 + a1*x + a2*x**2 + a3*x**3
2plt.plot(x,y,x,T3), plt.xlim([-3,3]), plt.ylim([0,5]);
3plt.show()

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مشتق توابع هذلولوی و معکوس آن‌ها — از صفر تا صد
• مشتق زنجیره ای — به زبان ساده
• مشتق مراتب بالاتر — از صفر تا صد

^^