در آموزشهای پیشین از مجموعه مطالب ریاضی مجله فرادرس ، با انتگرال سطحی و کاربردهای آن آشنا شدیم. همچنین، مفهوم میدان برداری را بیان کردیم. در این آموزش، انتگرال سطحی میدان برداری را بررسی میکنیم. این نوع انتگرال در زمینههای مختلفی مانند الکترومغناطیس کاربرد دارد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
انتگرال سطحی میدان برداری
میدان برداری F ( x , y , z ) \mathbf { F } \left ( { x , y , z } \right ) F ( x , y , z ) S S S بردار موقعیت زیر تعریف شده است:
r ( u , v ) = x ( u , v ) ⋅ i + y ( u , v ) ⋅ j + z ( u , v ) ⋅ k . \large { \mathbf { r } \left ( { u , v } \right ) } = { x \left ( { u , v } \right ) \cdot \mathbf { i } } + { y \left ( { u , v } \right ) \cdot \mathbf { j } } + { z \left ( { u , v } \right ) \cdot \mathbf { k } . } r ( u , v ) = x ( u , v ) ⋅ i + y ( u , v ) ⋅ j + z ( u , v ) ⋅ k .
فرض کنید توابع x ( u , v ) x\left( {u,v} \right) x ( u , v ) y ( u , v ) y\left( {u,v} \right) y ( u , v ) z ( u , v ) z\left( {u,v} \right) z ( u , v ) D ( u , v ) D\left( {u,v} \right) D ( u , v ) پیوسته و مشتقپذیر بوده و رتبه ماتریس زیر، 2 2 2
$$ \large \left [ { \begin {array} { * { 2 0 } { c } }<br />
{ \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial y } } { { \partial u } } } & { \frac { { \partial z } } { { \partial u } } } \\<br />
{ \frac { { \partial x } } { { \partial v } } } & { \frac { { \partial y } } { { \partial v } } } & { \frac { { \partial z } } { { \partial v } } }<br />
\end {array} } \right ] $$
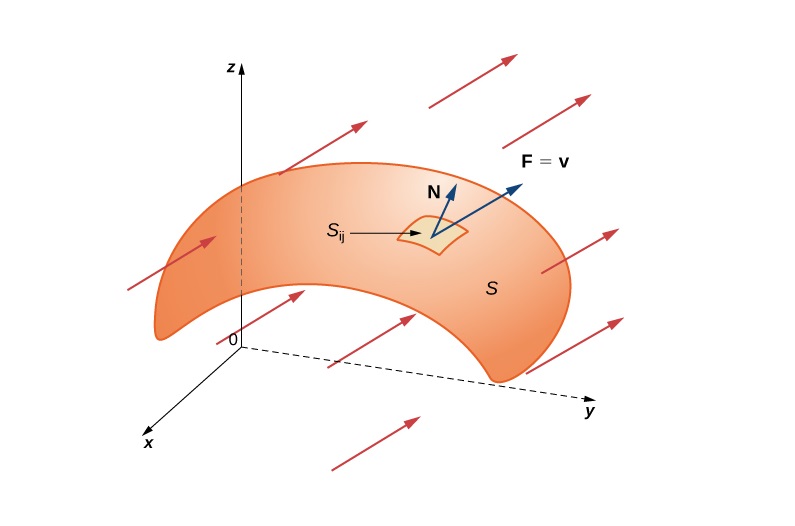
نماد n ( x , y , z ) \mathbf{n}\left( {x,y,z} \right) n ( x , y , z ) S S S ( x , y , z ) \left( {x,y,z} \right) ( x , y , z ) S S S n ( x , y , z ) \mathbf{n}\left( {x,y,z} \right) n ( x , y , z )
n ( x , y , z ) \large \mathbf { n } \left ( { x , y , z } \right ) n ( x , y , z ) − n ( x , y , z ) \large - \mathbf { n } \left ( { x , y , z } \right ) − n ( x , y , z )
اگر S S S
انتگرال سطحی میدان برداری F \mathbf{F} F S S S F \mathbf{F} F S S S
اگر سطح S S S
∬ S F ( x , y , z ) ⋅ d S = ∬ S F ( x , y , z ) ⋅ n d S = ∬ D ( u , v ) F ( x ( u , v ) , y ( u , v ) , z ( u , v ) ) ⋅ [ ∂ r ∂ u × ∂ r ∂ v ] d u d v ; \large \begin {align*} { \iint \limits _ S { \mathbf { F } \left ( { x , y , z } \right ) \cdot d \mathbf { S } } } & = { \iint \limits _ S \mathbf { F } \left ( { x , y , z } \right ) \cdot \mathbf { n } d S } \\ & = \kern0pt { \iint \limits _ { D \left ( { u , v } \right ) } { \mathbf { F } \left ( { x \left ( { u , v } \right ) , y \left ( { u , v } \right ) , z \left ( { u , v } \right ) } \right ) \cdot } \kern0pt { \left [ { \frac { { \partial \mathbf { r } } } { { \partial u } } \times \frac { { \partial \mathbf { r } } } { { \partial v } } } \right ] d u d v } ; } \end {align*} S ∬ F ( x , y , z ) ⋅ d S = S ∬ F ( x , y , z ) ⋅ n d S = D ( u , v ) ∬ F ( x ( u , v ) , y ( u , v ) , z ( u , v ) ) ⋅ [ ∂ u ∂ r × ∂ v ∂ r ] d u d v ;
اگر سطح S S S
∬ S F ( x , y , z ) ⋅ d S = ∬ S F ( x , y , z ) ⋅ n d S = ∬ D ( u , v ) F ( x ( u , v ) , y ( u , v ) , z ( u , v ) ) ⋅ [ ∂ r ∂ v × ∂ r ∂ u ] d u d v . \large \begin {align*} { \iint \limits _ S { \mathbf { F } \left ( { x , y , z } \right ) \cdot d \mathbf { S } } } & = { \iint \limits _ S \mathbf { F } \left ( { x , y , z } \right ) \cdot \mathbf { n } d S } \\ & = \kern0pt { \iint \limits _ { D \left ( { u , v } \right ) } { \mathbf { F } \left ( { x \left ( { u , v } \right ) , y \left ( { u , v } \right ) , z \left ( { u , v } \right ) } \right ) \cdot } \kern0pt { \left [ { \frac { { \partial \mathbf { r } } } { { \partial v } } \times \frac { { \partial \mathbf { r } } } { { \partial u } } } \right ] d u d v } . } \end {align*} S ∬ F ( x , y , z ) ⋅ d S = S ∬ F ( x , y , z ) ⋅ n d S = D ( u , v ) ∬ F ( x ( u , v ) , y ( u , v ) , z ( u , v ) ) ⋅ [ ∂ v ∂ r × ∂ u ∂ r ] d u d v .
در اینجا، d S = n d S d\mathbf{S} = \mathbf{n}dS d S = n d S ضرب داخلی بردارها را نشان میدهد. مشتقهای جزئی در فرمولها، به صورت زیر محاسبه میشوند:
∂ r ∂ u = ∂ x ∂ u ( u , v ) ⋅ i + ∂ y ∂ u ( u , v ) ⋅ j + ∂ z ∂ u ( u , v ) ⋅ k , ∂ r ∂ v = ∂ x ∂ v ( u , v ) ⋅ i + ∂ y ∂ v ( u , v ) ⋅ j + ∂ z ∂ v ( u , v ) ⋅ k . \large \begin {align*} { \frac { { \partial \mathbf { r } } } { { \partial u } } } & = { \frac { { \partial x } } { { \partial u } } \left ( { u , v } \right ) \cdot \mathbf { i } } + { \frac { { \partial y } } { { \partial u } } \left ( { u , v } \right ) \cdot \mathbf { j } } + { \frac { { \partial z } } { { \partial u } } \left ( { u , v } \right ) \cdot \mathbf { k } , } \\ { \frac { { \partial \mathbf { r } } } { { \partial v } } } & = { \frac { { \partial x } } { { \partial v } } \left ( { u , v } \right ) \cdot \mathbf { i } } + { \frac { { \partial y } } { { \partial v } } \left ( { u , v } \right ) \cdot \mathbf { j } } + { \frac { { \partial z } } { { \partial v } } \left ( { u , v } \right ) \cdot \mathbf { k } . } \end {align*} ∂ u ∂ r ∂ v ∂ r = ∂ u ∂ x ( u , v ) ⋅ i + ∂ u ∂ y ( u , v ) ⋅ j + ∂ u ∂ z ( u , v ) ⋅ k , = ∂ v ∂ x ( u , v ) ⋅ i + ∂ v ∂ y ( u , v ) ⋅ j + ∂ v ∂ z ( u , v ) ⋅ k .
اگر سطح S S S z = z ( x , y ) z = z\left( {x,y} \right) z = z ( x , y ) z ( x , y ) z (x, y ) z ( x , y ) D ( x , y ) D (x,y) D ( x , y ) F \mathbf{F} F S S S
اگر سطح S S S k k k
∬ S F ( x , y , z ) ⋅ d S = ∬ S F ( x , y , z ) ⋅ n d S = ∬ D ( x , y ) F ( x , y , z ) ⋅ ( – ∂ z ∂ x i – ∂ z ∂ y j + k ) d x d y ; \large \begin {align*} { \iint \limits _ S { \mathbf { F } \left ( { x , y , z } \right ) \cdot d \mathbf { S } } } & = { \iint \limits _ S { \mathbf { F } \left ( { x , y , z } \right ) \cdot \mathbf { n } d S } } \\ & = { \iint \limits _ { D \left ( { x , y } \right ) } { \mathbf { F } \left ( { x , y , z } \right ) \cdot } \kern0pt { \left ( { – \frac { { \partial z } } { { \partial x } } \mathbf { i } – \frac { { \partial z } } { { \partial y } } \mathbf { j } + \mathbf { k } } \right ) d x d y } ; } \end {align*} S ∬ F ( x , y , z ) ⋅ d S = S ∬ F ( x , y , z ) ⋅ n d S = D ( x , y ) ∬ F ( x , y , z ) ⋅ ( – ∂ x ∂ z i – ∂ y ∂ z j + k ) d x d y ;
اگر سطح S S S k k k
∬ S F ( x , y , z ) ⋅ d S = ∬ S F ( x , y , z ) ⋅ n d S = ∬ D ( x , y ) F ( x , y , z ) ⋅ ( ∂ z ∂ x i + ∂ z ∂ y j − k ) d x d y ; \large \begin {align*} { \iint \limits _ S { \mathbf { F } \left ( { x , y , z } \right ) \cdot d \mathbf { S } } } & = { \iint \limits _ S { \mathbf { F } \left ( { x , y , z } \right ) \cdot \mathbf { n } d S } } \\ & = { \iint \limits _ { D \left ( { x , y } \right ) } { \mathbf { F } \left ( { x , y , z } \right ) \cdot } \kern0pt { \left ( { \frac { { \partial z } } { { \partial x } } \mathbf { i } + \frac { { \partial z } } { { \partial y } } \mathbf { j } - \mathbf { k } } \right ) d x d y } ; } \end {align*} S ∬ F ( x , y , z ) ⋅ d S = S ∬ F ( x , y , z ) ⋅ n d S = D ( x , y ) ∬ F ( x , y , z ) ⋅ ( ∂ x ∂ z i + ∂ y ∂ z j − k ) d x d y ;
همچنین میتوانیم انتگرال سطحی میدانهای برداری را به شکل مختصات بنویسیم.
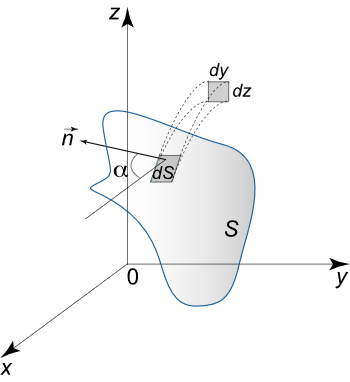
فرض کنید P ( x , y , z ) P\left( {x,y,z} \right) P ( x , y , z ) Q ( x , y , z ) Q\left( {x,y,z} \right) Q ( x , y , z ) R ( x , y , z ) R\left( {x,y,z} \right) R ( x , y , z ) F \mathbf{F} F cos α \cos \alpha cos α cos β \cos \beta cos β cos γ \cos \gamma cos γ n \mathbf{n} n x x x y y y z z z F ⋅ n \mathbf{F} \cdot \mathbf{n} F ⋅ n
F ⋅ n = F ( P , Q , R ) ⋅ n ( cos α , cos β , cos γ ) = P cos α + Q cos β + R cos γ . \large \begin {align*} { \mathbf { F } \cdot \mathbf { n } } & = { \mathbf { F } \left ( { P , Q , R } \right ) \cdot } \kern0pt { \mathbf { n } \left ( { \cos \alpha , \cos \beta , \cos \gamma } \right ) } \\ & = { P \cos \alpha + Q \cos \beta + R \cos \gamma . } \end {align*} F ⋅ n = F ( P , Q , R ) ⋅ n ( cos α , cos β , cos γ ) = P cos α + Q cos β + R cos γ .
در نتیجه، انتگرال سطحی را میتوان به فرم زیر نوشت:
∬ S ( F ⋅ n ) d S = ∬ S ( P cos α + Q cos β + R cos γ ) d S . \large { \iint \limits _ S { \left ( { \mathbf { F } \cdot \mathbf { n } } \right ) d S } } = { \iint \limits _ S { \left ( { P \cos \alpha + Q \cos \beta } \right . } + { \left . { R \cos \gamma } \right ) d S } . } S ∬ ( F ⋅ n ) d S = S ∬ ( P cos α + Q cos β + R cos γ ) d S .
از آنجایی که cos α ⋅ d S = d y d z \cos \alpha \cdot dS = dydz cos α ⋅ d S = d y d z cos β ⋅ d S = d z d x \cos \beta \cdot dS = dzdx cos β ⋅ d S = d z d x cos γ ⋅ d S = d x d y \cos \gamma \cdot dS = dxdy cos γ ⋅ d S = d x d y
∬ S ( F ⋅ n ) d S = ∬ S ( P cos α + Q cos β + R cos γ ) d S = ∬ S P d y d z + Q d z d x + R d x d y \large \begin {align*} {\iint\limits_S {\left( {\mathbf{F} \cdot \mathbf{n}} \right)dS} } & = {\iint\limits_S {\left( {P\cos \alpha + Q\cos \beta }\right.}+{\left.{ R\cos \gamma } \right)dS} }\\ & = { \iint \limits _ S { P d y d z + Q d z d x + R d x d y } } \end {align*} S ∬ ( F ⋅ n ) d S = S ∬ ( P cos α + Q cos β + R cos γ ) d S = S ∬ P d y d z + Q d z d x + R d x d y
شکل ۱ اگر سطح S S S r ( x ( u , v ) , y ( u , v ) , z ( u , v ) ) \mathbf{r}\big( {x\left( {u,v} \right),y\left( {u,v} \right)},{z\left( {u,v} \right)} \big) r ( x ( u , v ) , y ( u , v ) , z ( u , v ) )
$$ \large \begin {align*}<br />
{ \iint \limits _ S { \left ( { \mathbf { F } \cdot \mathbf { n } } \right ) d S } }<br />
& = { \iint \limits _ S { P d y d z + Q d z d x + R d x d y } }<br />
\\ & = { \iint \limits _ { D \left ( { u , v } \right ) } { \left | { \begin {array} { * { 2 0 } { c } }<br />
P & Q & R \\<br />
{ \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial y } } { { \partial u } } } & { \frac { { \partial z } } { { \partial u } } } \\<br />
{ \frac { { \partial x } } { { \partial v } } } & { \frac { { \partial y } } { { \partial v } } } & { \frac { { \partial z } } { { \partial v } } }<br />
\end {array} } \right | d u d v} }<br />
\end {align*} $$
که در آن، مختصات ( u , v ) (u, v ) ( u , v ) D ( u , v ) D\left( {u,v} \right) D ( u , v )
مثالها
در ادامه، چند مثال را بررسی میکنیم.
مثال ۱
شار میدان برداری F ( x , y , z ) = ( x , – 1 , z ) \mathbf{F}\left( {x,y,z} \right)= \left( {x, – 1,z} \right) F ( x , y , z ) = ( x , –1 , z ) S S S z = x cos y z = x\cos y z = x cos y 0 ≤ x ≤ 1 0 \le x \le 1 0 ≤ x ≤ 1 π 4 ≤ y ≤ π 3 {\large\frac{\pi }{4}\normalsize} \le y \le {\large\frac{\pi }{3}\normalsize} 4 π ≤ y ≤ 3 π
حل: از فرمول زیر استفاده میکنیم:
∬ S F ⋅ d S = ∬ D ( x , y ) F ⋅ ( ∂ z ∂ x i + ∂ z ∂ y j – k ) d x d y \large { \iint \limits _ S { \mathbf { F } \cdot d \mathbf { S } } \text { = } } \kern0pt { \iint \limits _ { D \left ( { x , y } \right ) } { \mathbf { F } \cdot } \kern0pt { \left ( { \frac { { \partial z } } { { \partial x } } \mathbf { i } + \frac { { \partial z } } { { \partial y } } \mathbf { j } – \mathbf { k } } \right ) d x d y } } S ∬ F ⋅ d S = D ( x , y ) ∬ F ⋅ ( ∂ x ∂ z i + ∂ y ∂ z j – k ) d x d y
روابط زیر را داریم:
∂ z ∂ x = ∂ ∂ x ( x cos y ) = cos y , ∂ z ∂ y = ∂ ∂ y ( x cos y ) = – x sin y \large \begin {align*} \frac { { \partial z } } { \partial x } & = \frac { \partial } { { \partial x } } \left ( { x \cos y } \right ) = { \cos y , \; \; \; } \kern0pt \\ \frac { \partial z } { \partial y } & = \frac { \partial } { { \partial y } } \left ( { x \cos y } \right ) = { – x \sin y } \end {align*} ∂ x ∂ z ∂ y ∂ z = ∂ x ∂ ( x cos y ) = cos y , = ∂ y ∂ ( x cos y ) = – x sin y
بنابراین، شار میدان برداری را میتوان به صورت زیر نوشت:
$$ \large \begin {align*}<br />
\require {cancel} \iint \limits _ S { \mathbf { F } \cdot d \mathbf { S } } & = \kern0pt { \iint \limits _ { D \left ( { x , y } \right ) } { \left [ { x \cdot \cos y } \right . } \kern0pt { + \left . { \left ( { – 1 } \right ) \cdot \left ( { – x \sin y } \right ) } \right . } \kern0pt { + \left . { z \cdot \left ( { – 1 } \right ) } \right ] d x d y } } \\ & = { { \iint \limits _ { D \left ( { x , y } \right ) } { \left ( { \cancel { x \cos y } } \right . } + { \left . { x \sin y } \right . } - { \left . { \cancel { x \cos y } } \right ) d x d y } } } \\ & = { \iint \limits _ { D \left ( { x , y } \right ) } { x \sin y d x d y } . }<br />
\end {align*} $$
پس از چند تبدیل ساده، جواب به دست میآید:
∬ S F ⋅ d S = ∫ 0 1 x d x ∫ π 4 π 3 sin y d y = [ ( x 2 2 ) ∣ 0 1 ] ⋅ [ ( – cos y ) ∣ π 4 π 3 ] = 1 2 ( – cos π 3 + cos π 4 ) = 1 2 ( – 1 2 + 2 2 ) = 2 – 1 4 . \large \begin {align*} { \iint \limits _ S { \mathbf { F } \cdot d \mathbf { S } } } & = { \int \limits _ 0 ^ 1 { x d x } \int \limits _ { \large \frac { \pi } { 4 } \normalsize } ^ { \large \frac { \pi } { 3 } \normalsize } { \sin y d y } } = { \left [ { \left . { \left ( { \frac { { { x ^2 } } } { 2 } } \right ) } \right | _ 0 ^ 1 } \right ] \cdot \left [ { \left . { \left ( { – \cos y } \right ) } \right | _ { \large \frac { \pi }{ 4 } \normalsize } ^ { \large \frac { \pi } { 3 } \normalsize } } \right ] } \\ & = { \frac { 1 } { 2 } \left ( { – \cos \frac { \pi } { 3 } + \cos \frac { \pi } { 4 } } \right ) } = { \frac { 1 } { 2 } \left ( { – \frac { 1 } { 2 } + \frac { { \sqrt 2 } } { 2 } } \right ) } = { \frac { { \sqrt 2 – 1 } } { 4 } . } \end {align*} S ∬ F ⋅ d S = 0 ∫ 1 x d x 4 π ∫ 3 π sin y d y = ( 2 x 2 ) 0 1 ⋅ [ ( – cos y ) ∣ 4 π 3 π ] = 2 1 ( – cos 3 π + cos 4 π ) = 2 1 ( – 2 1 + 2 2 ) = 4 2 –1 .
مثال ۲
شار میدان برداری F ( x , y , z ) = ( y , x , z ) \mathbf{F}\left( {x,y,z} \right)= \left( {y,x,z} \right) F ( x , y , z ) = ( y , x , z ) S S S r ( u , v ) = ( cos v , sin v , u ) \mathbf{r}\left( {u,v} \right) =\left( {\cos v,\sin v,u} \right) r ( u , v ) = ( cos v , sin v , u ) 0 ≤ u ≤ 2 0 \le u \le 2 0 ≤ u ≤ 2 π 2 ≤ v ≤ π {\large\frac{\pi }{2}\normalsize} \le v \le \pi 2 π ≤ v ≤ π
حل: ابتدا مشتقات جزئی را محاسبه میکنیم:
∂ r ∂ u = ( 0 , 0 , 1 ) , ∂ r ∂ v = ( – sin v , cos v , 0 ) . \large { \frac { { \partial \mathbf { r } } } { { \partial u } } = \left ( { 0 , 0 , 1 } \right) , \; \; \; } \kern0pt { \frac { { \partial \mathbf { r } } } { { \partial v } } = \left ( { – \sin v , \cos v , 0 } \right ) . } ∂ u ∂ r = ( 0 , 0 , 1 ) , ∂ v ∂ r = ( – sin v , cos v , 0 ) .
ضرب برداری این مشتقات به صورت زیر است:
$$ \large \begin {align*}<br />
{ \frac { { \partial \mathbf { r } } } { { \partial u } } \times \frac { { \partial \mathbf { r } } } { { \partial v } } }<br />
& = { \left | { \begin {array} { * { 2 0 } { c } }<br />
\mathbf { i } & \mathbf { j } & \mathbf { k } \\<br />
0 & 0 & 1 \\<br />
{ – \sin v } & { \cos v } & 0<br />
\end {array} } \right | } \\ &<br />
= { – \cos v \cdot \mathbf { i } – \sin v \cdot \mathbf { j } . }<br />
\end {align*} $$
در نتیجه، المان سطح برداری برابر است با:
d S = [ ∂ r ∂ u × ∂ r ∂ v ] d u d v = ( – cos v , – sin v , 0 ) d u d v . \large { d \mathbf { S } = \left [ { \frac { { \partial \mathbf { r } } } { { \partial u } } \times \frac { { \partial \mathbf { r } } } { { \partial v } } } \right ] d u d v } = { \left ( { – \cos v , – \sin v , 0 } \right ) d u d v . } d S = [ ∂ u ∂ r × ∂ v ∂ r ] d u d v = ( – cos v , – sin v , 0 ) d u d v .
از آنجایی که x = cos v x = \cos v x = cos v y = sin v y = \sin v y = sin v z = v z = v z = v F \mathbf{F} F
F ( r , u , v ) = ( sin v , cos v , u ) . \large { \mathbf { F } \left ( { r , u , v } \right ) } = { \left ( { \sin v , \cos v , u } \right ) . } F ( r , u , v ) = ( sin v , cos v , u ) .
در نهایت، انتگرال سطح S S S
∬ S F ⋅ d S = ∬ D ( u , v ) [ sin v ⋅ ( – cos v ) + cos v ⋅ ( – sin v ) + 0 ] d u d v = ∬ D ( u , v ) ( – 2 sin v cos v ) d u d v = – ∫ 0 2 d u ∫ π 2 π sin 2 v d v = – 2 ⋅ [ ( – cos 2 v 2 ) ∣ π 2 π ] = cos 2 π – cos π = 2. \large \begin {align*} { \iint \limits _ S { \mathbf { F } \cdot d \mathbf { S } } } & = { \iint \limits _ { D \left ( { u , v } \right ) } { \left [ { \sin v \cdot \left ( { – \cos v } \right ) } \right . } } + { { \left . { \cos v \cdot \left ( { – \sin v } \right ) + 0 } \right ] d u d v } } \\ & = { \iint \limits _ { D \left ( { u , v } \right ) } { \left ( { – 2 \sin v \cos v } \right ) d u d v } } = { – \int \limits _ 0 ^ 2 { d u } \int \limits _ { \large \frac { \pi } { 2 } \normalsize } ^ \pi { \sin 2 v d v } } \\ & = { – 2 \cdot \left [ { \left . { \left ( { – \frac { { \cos 2 v } } { 2 } } \right ) } \right | _ { \large \frac { \pi }{ 2 } \normalsize } ^ \pi } \right ] } = { \cos 2 \pi – \cos \pi } = { 2 . } \end {align*} S ∬ F ⋅ d S = D ( u , v ) ∬ [ sin v ⋅ ( – cos v ) + cos v ⋅ ( – sin v ) + 0 ] d u d v = D ( u , v ) ∬ ( –2 sin v cos v ) d u d v = – 0 ∫ 2 d u 2 π ∫ π sin 2 v d v = –2 ⋅ ( – 2 cos 2 v ) 2 π π = cos 2 π – cos π = 2.
مثال ۳
شار میدان برداری F = y ⋅ i – x ⋅ j + z ⋅ k \mathbf { F } = y \cdot \mathbf { i } – x \cdot \mathbf { j } + z \cdot \mathbf { k } F = y ⋅ i – x ⋅ j + z ⋅ k z = x 2 + y 2 z= \sqrt {{x^2} + {y^2}} z = x 2 + y 2 0 ≤ z ≤ 2 0 \le z \le 2 0 ≤ z ≤ 2
حل: سطح مخروط با بردار r \mathbf{r} r
r ( x , y ) = x ⋅ i + y ⋅ j + x 2 + y 2 ⋅ k . \large { \mathbf { r } \left ( { x , y } \right ) = x \cdot \mathbf { i } + y \cdot \mathbf { j } } + { \sqrt { { x ^ 2 } + { y ^ 2 } } \cdot \mathbf { k } . } r ( x , y ) = x ⋅ i + y ⋅ j + x 2 + y 2 ⋅ k .
دامنه انتگرالگیری D ( x , y ) D\left( {x,y} \right) D ( x , y )
x 2 + y 2 ≤ 4. \large { { x ^ 2 } + { y ^ 2 } } \le 4 . x 2 + y 2 ≤ 4.
در ادامه، المان سطح برداری d S d\mathbf{S} d S
∂ r ∂ x = 1 ⋅ i + x x 2 + y 2 ⋅ k , ∂ r ∂ y = 1 ⋅ j + y x 2 + y 2 ⋅ k . \large { { \frac { { \partial \mathbf { r } } } { { \partial x } } = 1 \cdot \mathbf { i } } + { \frac { x } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } \cdot \mathbf { k } , \; \; \; } } \kern0pt { { \frac { { \partial \mathbf { r } } } { { \partial y } } = 1 \cdot \mathbf { j } } + { \frac { y } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } \cdot \mathbf { k } . } } ∂ x ∂ r = 1 ⋅ i + x 2 + y 2 x ⋅ k , ∂ y ∂ r = 1 ⋅ j + x 2 + y 2 y ⋅ k .
در نتیجه، داریم:
$$ \large \begin {align*}<br />
{ \frac { { \partial \mathbf { r } } } { { \partial x } } \times \frac { { \partial \mathbf { r } } } { { \partial y } } }<br />
& = { \left | { \begin {array} { * { 2 0 } { c } }<br />
\mathbf { i } & \mathbf { j } & \mathbf { k } \\<br />
1 & 0 & { \frac { x } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } } \\<br />
0 & 1 & { \frac { y } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } }<br />
\end {array} } \right | } \\ &<br />
= { – \frac { x } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } \cdot \mathbf { i } } - { \frac { y } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } \cdot \mathbf { j } + \mathbf { k } }<br />
\end {align*} $$
بنابراین، المان سطح برداری برابر است با:
d S = ( – x x 2 + y 2 , – y x 2 + y 2 , 1 ) d x d y . \large { d \mathbf { S } = \left ( { – \frac { x } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } , } \right . } \kern0pt { \left . { – \frac { y } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } , 1 } \right ) d x d y . } d S = ( – x 2 + y 2 x , – x 2 + y 2 y , 1 ) d x d y .
میدان برداری F \mathbf{F} F
F ( x , y , z ) = y ⋅ i – x ⋅ j + x 2 + y 2 ⋅ k . \large { \mathbf { F } \left ( { x , y , z } \right ) } = { y \cdot \mathbf { i } – x \cdot \mathbf { j } } + { \sqrt { { x ^ 2 } + { y ^ 2 } } \cdot \mathbf { k } . } F ( x , y , z ) = y ⋅ i – x ⋅ j + x 2 + y 2 ⋅ k .
در نتیجه، شار میدان برداری گذرنده از S S S
I = ∬ S F ⋅ d S = ∬ D ( x , y ) [ y ⋅ ( – x x 2 + y 2 ) + ( – x ) ⋅ ( – y x 2 + y 2 ) + x 2 + y 2 ⋅ 1 ] d x d y = ∬ D ( x , y ) x 2 + y 2 d x d y . \large \begin {align*} I & = \iint\limits_S {\mathbf{F} \cdot d\mathbf{S}} = {\iint\limits_{D\left( {x,y} \right)} {\Big[ {y \cdot \Big( { – \frac{x}{{\sqrt {{x^2} + {y^2}} }}} \Big) }}}+{{{ \left( { – x} \right) \cdot \Big( { – \frac{y}{{\sqrt {{x^2} + {y^2}} }}} \Big) }}} \\ & \, \, \, \, \, \, \, \,\, \, \, \, \, \, \, \,\, \, \, \, \, \, \, \,\, \, \, \, \, \, \,\, \,\, \, \, \, \, \, \, \,\, \, \, \, \, +{{{ \sqrt {{x^2} + {y^2}} \cdot 1} \Big]dxdy} } = {\iint\limits_{D\left( {x,y} \right)} {\sqrt {{x^2} + {y^2}} dxdy} .} \end {align*} I = S ∬ F ⋅ d S = D ( x , y ) ∬ [ y ⋅ ( – x 2 + y 2 x ) + ( – x ) ⋅ ( – x 2 + y 2 y ) + x 2 + y 2 ⋅ 1 ] d x d y = D ( x , y ) ∬ x 2 + y 2 d x d y .
با تغییر مختصت دکارتی به قطبی ، داریم:
I = ∫ 0 2 π d φ ∫ 0 2 r 2 d r = 2 π [ ( r 3 3 ) ∣ 0 2 ] = 16 π 3 . \large { I = \int \limits _ 0 ^ { 2 \pi } { d \varphi } \int \limits _ 0 ^ 2 { { r ^ 2 } d r } } = { 2 \pi \left [ { \left . { \left ( { \frac { { { r ^ 3 } } } { 3 } } \right ) } \right | _ 0 ^ 2 } \right ] } = { \frac { { 16 \pi } } { 3 } . } I = 0 ∫ 2 π d φ 0 ∫ 2 r 2 d r = 2 π ( 3 r 3 ) 0 2 = 3 16 π .
مثال ۴
شار میدان برداری F ( x , y , z ) = – y ⋅ i + x ⋅ j − z ⋅ k \mathbf { F } \left ( { x , y , z } \right ) = – y \cdot \mathbf { i } + x \cdot \mathbf { j } - z \cdot \mathbf { k } F ( x , y , z ) = – y ⋅ i + x ⋅ j − z ⋅ k کره واحد x 2 + y 2 + z 2 = 1 { x ^ 2 } + { y ^ 2 } + { z ^ 2 } = 1 x 2 + y 2 + z 2 = 1
حل: عبارت زیر، معادله پارامتری کره واحد را در دستگاه مختصات کروی نشان میدهد:
r ( ψ , θ ) = cos ψ sin θ ⋅ i + sin ψ sin θ ⋅ j + cos θ ⋅ k \large { \mathbf { r } \left ( { \psi , \theta } \right ) } = { \cos \psi \sin \theta \cdot \mathbf { i } } + { \sin \psi \sin \theta \cdot \mathbf { j } } + { \cos \theta \cdot \mathbf { k } } r ( ψ , θ ) = cos ψ sin θ ⋅ i + sin ψ sin θ ⋅ j + cos θ ⋅ k
که در آن 0 ≤ ψ ≤ 2 π 0 \le \psi \le 2\pi 0 ≤ ψ ≤ 2 π 0 ≤ θ ≤ π 0 \le \theta \le \pi 0 ≤ θ ≤ π F \mathbf{F} F
F ( r , ψ , θ ) = – sin ψ sin θ ⋅ i + cos ψ sin θ ⋅ j − cos θ ⋅ k \large { \mathbf { F } \left ( { r , \psi , \theta } \right ) } = { – \sin \psi \sin \theta \cdot \mathbf { i } } + { \cos \psi \sin \theta \cdot \mathbf { j } } - { \cos \theta \cdot \mathbf { k } } F ( r , ψ , θ ) = – sin ψ sin θ ⋅ i + cos ψ sin θ ⋅ j − cos θ ⋅ k
در ادامه، المان سطح برداری d S d\mathbf{S} d S
∂ r ∂ ψ = – sin ψ sin θ ⋅ i + cos ψ sin θ ⋅ j + 0 ⋅ k , ∂ r ∂ θ = cos ψ sin θ ⋅ i + sin ψ cos θ ⋅ j − sin θ ⋅ k . \large \begin {align*} { \frac { { \partial \mathbf { r } } } { { \partial \psi } } } & = { – \sin \psi \sin \theta \cdot \mathbf { i } } + { \cos \psi \sin \theta \cdot \mathbf { j } } + { 0 \cdot \mathbf { k } , } \\ { \frac { { \partial \mathbf { r } } } { { \partial \theta } } } & = { \cos \psi \sin \theta \cdot \mathbf { i } } + { \sin \psi \cos \theta \cdot \mathbf { j } } - { \sin \theta \cdot \mathbf { k } . } \end {align*} ∂ ψ ∂ r ∂ θ ∂ r = – sin ψ sin θ ⋅ i + cos ψ sin θ ⋅ j + 0 ⋅ k , = cos ψ sin θ ⋅ i + sin ψ cos θ ⋅ j − sin θ ⋅ k .
بنابراین، داریم:
$$ \large \begin {align*}<br />
\frac { { \partial \mathbf { r } } } { { \partial \psi } } \times \frac { { \partial \mathbf { r } } } { { \partial \theta } } & = \kern0pt<br />
{ \left | { \begin {array} { * { 2 0 } { c } }<br />
\mathbf { i } & \mathbf { j } & \mathbf { k } \\<br />
{ – \sin \psi \sin \theta } & { \cos \psi \sin \theta } & 0 \\<br />
{ \cos \psi \cos \theta } & { \sin \psi \cos \theta } & { – \sin \theta }<br />
\end {array} } \right | \; } \\<br />
& = { – \cos \psi \, { \sin ^2 } \theta \cdot \mathbf { i } } - { \sin \psi \, { \sin ^ 2 } \theta \cdot \mathbf { j } }<br />
\\ & \, \, \, \, \, \, \, \, \, \, – { \left ( { { { \sin } ^ 2 } \psi \sin \theta \cos \theta }\right . } + { \left . { { { \cos } ^ 2 } \psi \sin \theta \cos \theta } \right ) \cdot \mathbf { k } } \\<br />
& = { – \cos \psi \, { \sin ^ 2 } \theta \cdot \mathbf { i } } - { \sin \psi \, { \sin ^ 2 } \theta \cdot \mathbf { j } }<br />
– { \sin \theta \cos \theta \cdot \mathbf { k } . }<br />
\end {align*} $$
در نتیجه، المان سطح برداری d S d\mathbf{S} d S
d S = ( – cos ψ sin 2 θ , – sin ψ sin 2 θ , – sin θ cos θ ) d ψ d θ . \large { d \mathbf { S } \text { = } } \kern0pt { \left ( { – \cos \psi \, { { \sin } ^ 2 } \theta , – \sin \psi \, { { \sin } ^ 2 } \theta , } \right . } \kern0pt { \left . { – \sin \theta \cos \theta } \right ) d \psi d \theta . } d S = ( – cos ψ sin 2 θ , – sin ψ sin 2 θ , – sin θ cos θ ) d ψ d θ .
در نهایت، انتگرال سطحی (شار میدان برداری) به صورت زیر محاسبه میشود:
∬ S F ( r , ψ , θ ) ⋅ d S = ∬ D ( ψ , θ ) [ ( – sin ψ sin θ ) ⋅ ( – cos ψ sin 2 θ ) + cos ψ sin θ ⋅ ( – sin ψ sin 2 θ ) + ( – cos θ ) ⋅ ( – cos θ sin θ ) ] d ψ d θ = ∫ D ( ψ , θ ) [ sin ψ cos ψ sin 3 θ − sin ψ cos ψ sin 3 θ + sin θ cos 2 θ ] d ψ d θ = ∫ D ( ψ , θ ) sin θ cos 2 θ d ψ d θ = ∫ 0 2 π d ψ ∫ 0 π sin θ cos 2 θ d θ = – 2 π ∫ 0 π cos 2 θ d ( cos θ ) = – 2 π [ ( cos 3 θ 3 ) ∣ 0 π ] = – 2 π 3 ( cos 3 π – cos 3 0 ) = 4 π 3 . \large \begin {align*} { \iint \limits _ S \mathbf { F } \left ( {r,\psi ,\theta } \right) \cdot d \mathbf { S } } & = \kern0pt { \iint \limits _ { D \left ( { \psi , \theta } \right ) } { \left [ { \left ( { – \sin \psi \sin \theta } \right ) \cdot } \kern0pt { \left ( { – \cos \psi \, { { \sin } ^ 2 } \theta } \right ) } \right . } } \\ & \, \, \, \, \, \, \, + { \cos \psi \sin \theta \cdot } \kern0pt { \left ( { – \sin \psi \, { { \sin } ^ 2 } \theta } \right ) } + { { \left . { \left ( { – \cos \theta } \right ) \cdot } \kern0pt { \left ( { – \cos \theta \sin \theta } \right ) } \right ] d \psi d \theta } } \\ & = { { \int \limits _ { D \left ( { \psi , \theta } \right ) } { \left [ { \sin \psi \cos \psi \, { { \sin } ^ 3 } \theta } \right . } - { \left . { \sin \psi \cos \psi \, { { \sin } ^ 3 } \theta } \right . } } } \kern0pt { { \left . { + \sin \theta \, { { \cos } ^ 2 } \theta } \right ] d \psi d \theta } } \\ & = { \int \limits _ { D \left ( { \psi , \theta } \right ) } { \sin \theta \, { { \cos } ^ 2 } \theta d \psi d \theta } } = { \int \limits _ 0 ^ { 2 \pi } { d \psi } \int \limits _ 0 ^ \pi { \sin \theta \, { { \cos } ^ 2 } \theta d \theta } } = { – 2 \pi \int \limits _ 0 ^ \pi { { { \cos } ^ 2 } \theta d \left ( { \cos \theta } \right ) } } \\ & = { – 2 \pi \left [ { \left . { \left ( { \frac { { { { \cos } ^ 3 } \theta } } { 3 } } \right ) } \right | _ 0 ^ \pi } \right ] } = { – \frac { { 2 \pi } } { 3 } \left ( { { { \cos } ^ 3 } \pi – { { \cos } ^ 3 } 0 } \right ) } = { \frac { { 4 \pi } } { 3 } . } \end {align*} S ∬ F ( r , ψ , θ ) ⋅ d S = D ( ψ , θ ) ∬ [ ( – sin ψ sin θ ) ⋅ ( – cos ψ sin 2 θ ) + cos ψ sin θ ⋅ ( – sin ψ sin 2 θ ) + ( – cos θ ) ⋅ ( – cos θ sin θ ) ] d ψ d θ = D ( ψ , θ ) ∫ [ sin ψ cos ψ sin 3 θ − sin ψ cos ψ sin 3 θ + sin θ cos 2 θ ] d ψ d θ = D ( ψ , θ ) ∫ sin θ cos 2 θ d ψ d θ = 0 ∫ 2 π d ψ 0 ∫ π sin θ cos 2 θ d θ = –2 π 0 ∫ π cos 2 θ d ( cos θ ) = –2 π [ ( 3 cos 3 θ ) 0 π ] = – 3 2 π ( cos 3 π – cos 3 0 ) = 3 4 π .
مثال ۵
انتگرال سطحی ∬ S d y d z x + d z d x y + d x d y z \iint\limits_S {{\large\frac{{dydz}}{x}\normalsize} + {\large\frac{{dzdx}}{y}\normalsize} }+{ {\large\frac{{dxdy}}{z}\normalsize}} S ∬ x d y d z + y d z d x + z d x d y S S S r ( u , v ) = ( a cos u cos v , b sin u cos v , c sin v ) \mathbf{r}\left( {u,v} \right) =\big( {a\cos u\cos v,}{b\sin u\cos v,}{c\sin v} \big) r ( u , v ) = ( a cos u cos v , b sin u cos v , c sin v ) u u u v v v 0 ≤ u ≤ 1 0 \le u \le 1 0 ≤ u ≤ 1 0 ≤ v ≤ π 2 0 \le v \le {\large\frac{\pi }{2}\normalsize} 0 ≤ v ≤ 2 π
حل: از فرمول زیر استفاده میکنیم:
$$ \large { { \iint \limits _ S { P d y d z + Q d z d x } + { R d x d y } } }<br />
= { \iint \limits _ { D \left ( { u , v } \right ) } { \left | { \begin {array} { * { 2 0 } { c } }<br />
P & Q & R \\<br />
{ \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial y } } { { \partial u } } } & { \frac { { \partial z } } { { \partial u } } } \\<br />
{ \frac { { \partial x } } { { \partial v } } } & { \frac { { \partial y } } { { \partial v } } } & { \frac { { \partial z } } { { \partial v } } }<br />
\end {array} } \right | d u d v } . } $$
مشتقات جزئی به صورت زیر هستند:
∂ x ∂ u = ∂ ∂ u ( a cos u cos v ) = – a sin u cos v , ∂ y ∂ u = ∂ ∂ u ( b sin u cos v ) = b cos u cos v , ∂ z ∂ u = ∂ ∂ u ( c sin v ) = 0 , ∂ x ∂ v = ∂ ∂ v ( a cos u cos v ) = – a cos u sin v , ∂ y ∂ v = ∂ ∂ v ( b sin u cos v ) = – b sin u sin v , ∂ z ∂ v = ∂ ∂ v ( c sin v ) = c cos v , \large \begin {align*} \frac { { \partial x } } { { \partial u } } & = \frac{\partial }{{\partial u}}\left( {a\cos u\cos v} \right) ={ – a\sin u\cos v,} \\ \frac { { \partial y } } { { \partial u } } & = \frac { \partial }{ { \partial u } } \left ( { b \sin u \cos v } \right ) = { b \cos u \cos v , } \\ \frac { { \partial z } } { { \partial u } } & = \frac{\partial } { { \partial u } } \left ( { c \sin v } \right ) = { 0 , } \\ \frac { { \partial x } } { { \partial v } } & = \frac { \partial }{{\partial v}}\left( {a\cos u\cos v} \right) ={ – a\cos u\sin v,} \\ \frac { { \partial y } } { { \partial v } } & = \frac { \partial } { { \partial v } } \left ( { b \sin u \cos v } \right ) = { – b \sin u \sin v , } \\ \frac { { \partial z } } { { \partial v } } & = \frac { \partial } { { \partial v } } \left ( { c \sin v } \right ) = { c \cos v , } \end {align*} ∂ u ∂ x ∂ u ∂ y ∂ u ∂ z ∂ v ∂ x ∂ v ∂ y ∂ v ∂ z = ∂ u ∂ ( a cos u cos v ) = – a sin u cos v , = ∂ u ∂ ( b sin u cos v ) = b cos u cos v , = ∂ u ∂ ( c sin v ) = 0 , = ∂ v ∂ ( a cos u cos v ) = – a cos u sin v , = ∂ v ∂ ( b sin u cos v ) = – b sin u sin v , = ∂ v ∂ ( c sin v ) = c cos v ,
دترمینان نیز به صورت زیر نوشته میشود:
$$ \large \begin {align*}<br />
\left| { \begin {array} { * { 2 0 } { c} }<br />
{ \frac { 1 } { x} } & { \frac { 1 } { y } } & { \frac { 1 }{ z } } \\<br />
{ \frac { { \partial x } } { { \partial u } } } & { \frac { { \partial y } } { { \partial u } } } & { \frac { { \partial z } } { { \partial u } } } \\<br />
{ \frac { { \partial x } } { { \partial v } } } & { \frac { { \partial y } } { { \partial v } } } & { \frac { { \partial z } } { { \partial v } } }<br />
\end {array} } \right | & = \kern0pt<br />
{ \left| { \begin {array} { * { 2 0 } { c } }<br />
{ \frac { 1 } { { a \cos u \cos v } } } & { \frac { 1 } { { b \sin u \cos v } } } & { \frac { 1 }{ { c \sin v } } } \\<br />
{ \text { – } { \small { a \sin u \cos v } \normalsize } } & { \small { b \cos u\cos v}\normalsize } & { \small { 0 } \normalsize } \\<br />
{ \text { – } { \small { a\cos u\sin v}\normalsize}}&{\text{-}{ \small { b \sin u \sin v } \normalsize } } & { \small { c \cos v } \normalsize }<br />
\end{array} } \right | } \\ &<br />
= { { \frac { 1 } { { a \cos u \cos v } } \cdot } \kern0pt { b \cos u \cos v \cdot c \cos v } }<br />
+ { { \frac { 1 } { { b \sin u \cos v } } \cdot } \kern0pt { a \sin u \cos v \cdot c\cos v }}\\ & \,\,\,\,\,\,\,\,<br />
+ { { \frac { 1 } { { c \sin v } } \left ( { a \sin u \cos v \cdot } \kern0pt { b \sin u \sin v } \right . } }<br />
+ { { \left . { a \cos u \sin v \cdot } \kern0pt { b \cos u \cos v } \right ) } } \\ &<br />
= { { \frac { { b c } } { a } \cos v + \frac { { a c } } { b } \cos v } + { \frac { { a b } } { c } \left ( { { { \sin } ^ 2 } u \cos v } \right . } } + { { \left . { { { \cos } ^ 2 } u \cos v } \right ) } } \\ &<br />
= { \left ( { \frac { { a b } } { c } + \frac { { a c } } { b } + \frac { { b c } } { a } } \right ) \cos v . }<br />
\end {align*} $$
در نتیجه، انتگرال سطح برابر است با:
I = ∬ D ( u , v ) ( a b c + a c b + b c a ) cos v d u d v = ( a b c + a c b + b c a ) ⋅ ∫ 0 1 d u ∫ 0 π 2 cos v d v = ( a b c + a c b + b c a ) ⋅ [ ( sin v ) ∣ 0 π 2 ] = a b c + a c b + b c a . \large \begin {align*} I & = \kern0pt { \iint \limits _ { D \left ( { u , v } \right ) } { \left ( { \frac { { a b } } { c } + \frac { { a c } } { b } + \frac { { b c } } { a } } \right ) \cos v d u d v } } \\ & = { \left ( { \frac {{ a b } } { c } + \frac { { a c } } { b } + \frac { { b c } } { a } } \right ) \cdot } \kern0pt { \int \limits _ 0 ^ 1 { d u} \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \cos v d v } } \\ & = { \left ( { \frac { { a b } } { c } + \frac { { a c } } { b } + \frac { { b c } } { a } } \right ) \cdot } \kern0pt { \left [ { \left . { \left ( { \sin v } \right ) } \right | _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } } \right ] } \\ & = { \frac { { a b } } { c } + \frac { { a c } } { b } + \frac { { b c } } { a } . } \end {align*} I = D ( u , v ) ∬ ( c ab + b a c + a b c ) cos v d u d v = ( c ab + b a c + a b c ) ⋅ 0 ∫ 1 d u 0 ∫ 2 π cos v d v = ( c ab + b a c + a b c ) ⋅ [ ( sin v ) ∣ 0 2 π ] = c ab + b a c + a b c .
مثال ۶
انتگرال سطحی ∬ S 2 x d y d z \iint\limits_S {2xdydz} S ∬ 2 x d y d z S S S x 2 + y 2 + z 2 = a 2 { x ^ 2 } + { y ^ 2 } + { z ^ 2 } = { a ^ 2 } x 2 + y 2 + z 2 = a 2
حل: ابتدا مؤلفههای میدان برداری F \mathbf{F} F
F ( P , Q , R ) = ( 2 x , 0 , 0 ) . \large \mathbf { F } \left ( { P , Q , R } \right ) = \left ( { 2 x , 0 , 0 } \right ) . F ( P , Q , R ) = ( 2 x , 0 , 0 ) .
تبدیل معادله کره از مختصات دکارتی به مختصات کروی، محاسبات را ساده خواهد کرد. بنابراین، داریم:
r ( ψ , θ ) = a cos ψ sin θ ⋅ i + a sin ψ sin θ ⋅ j + a cos θ ⋅ k \large { \mathbf { r } \left ( { \psi , \theta } \right ) } = { a \cos \psi \sin \theta \cdot \mathbf { i } } + { a \sin \psi \sin \theta \cdot \mathbf { j } } + { a \cos \theta \cdot \mathbf { k } } r ( ψ , θ ) = a cos ψ sin θ ⋅ i + a sin ψ sin θ ⋅ j + a cos θ ⋅ k
که در آن 0 ≤ ψ ≤ 2 π 0 \le \psi \le 2\pi 0 ≤ ψ ≤ 2 π 0 ≤ θ ≤ π 0 \le \theta \le \pi 0 ≤ θ ≤ π
$$ \large { { \iint \limits _ S { P d y d z + Q d z d x } + { R d x d y } } }<br />
= { \iint \limits _ { D \left ( {\psi , \theta } \right ) } { \left | { \begin {array} { * { 2 0 } { c } }<br />
P & Q & R \\<br />
{ \frac { { \partial x } } { { \partial \psi } } } & { \frac { { \partial y } } { { \partial \psi } } } & { \frac { { \partial z } } { { \partial \psi } } } \\<br />
{ \frac { { \partial x } } { { \partial \theta } } } & { \frac { { \partial y } } { { \partial \theta } } } & { \frac { { \partial z } } { { \partial \theta } } }<br />
\end {array} } \right | d \psi d \theta } . } $$
مشتقات جزئی فرمول بالا، به صورت زیر هستند:
∂ x ∂ ψ = ∂ ∂ ψ ( a cos ψ sin θ ) = – a sin ψ sin θ , ∂ y ∂ ψ = ∂ ∂ ψ ( a sin ψ sin θ ) = a cos ψ sin θ , ∂ z ∂ ψ = ∂ ∂ ψ ( a cos θ ) = 0 , ∂ x ∂ θ = ∂ ∂ θ ( a cos ψ sin θ ) = a cos ψ cos θ , ∂ y ∂ θ = ∂ ∂ θ ( a sin ψ sin θ ) = a cos ψ cos θ , ∂ z ∂ θ = ∂ ∂ θ ( a cos θ ) = – a sin θ \large \begin {align*} \frac { { \partial x } } { { \partial \psi } } & = \frac{\partial }{{\partial \psi }}\left( {a\cos \psi \sin \theta } \right) = – a\sin \psi \sin \theta , \\ \frac{{\partial y}}{{\partial \psi }} & = \frac{\partial }{{\partial \psi }}\left( {a\sin \psi \sin \theta } \right) ={ a\cos \psi \sin \theta ,} \\ \frac{{\partial z}}{\partial \psi } & = \frac{\partial }{{\partial \psi }}\left( {a\cos \theta } \right) ={ 0,} \\ \frac { { \partial x } } { { \partial \theta } } & = \frac { \partial } { { \partial \theta } } \left ( { a \cos \psi \sin \theta } \right ) = { a \cos \psi \cos \theta , } \\ \frac { { \partial y } } { { \partial \theta } } & = \frac { \partial } { { \partial \theta } } \left ( { a \sin \psi \sin \theta } \right ) = { a \cos \psi \cos \theta , } \\ \frac { { \partial z } } { { \partial \theta } } & = \frac { \partial }{ { \partial \theta } } \left ( { a \cos \theta } \right ) = { – a \sin \theta } \end {align*} ∂ ψ ∂ x ∂ ψ ∂ y ∂ ψ ∂ z ∂ θ ∂ x ∂ θ ∂ y ∂ θ ∂ z = ∂ ψ ∂ ( a cos ψ sin θ ) = – a sin ψ sin θ , = ∂ ψ ∂ ( a sin ψ sin θ ) = a cos ψ sin θ , = ∂ ψ ∂ ( a cos θ ) = 0 , = ∂ θ ∂ ( a cos ψ sin θ ) = a cos ψ cos θ , = ∂ θ ∂ ( a sin ψ sin θ ) = a cos ψ cos θ , = ∂ θ ∂ ( a cos θ ) = – a sin θ
دترمینان انتگرال دوگانه نیز برابر است با:
$$ \large \begin {align*}<br />
\left | { \begin {array} { * { 2 0 } { c } }<br />
P & Q & R \\<br />
{ \frac { { \partial x } } { { \partial \psi } } } & { \frac { { \partial y } } { { \partial \psi } } } & { \frac { { \partial z } } { { \partial \psi } } } \\<br />
{ \frac { { \partial x } } { { \partial \theta } } } & { \frac { { \partial y } } { { \partial \theta } } } & { \frac { { \partial z } } { { \partial \theta } } }<br />
\end {array}} \right | & = \kern0pt<br />
{ \small { \left | { \begin {array} { * { 2 0 } { c } }<br />
{ 2 a \cos \psi \sin \theta } & 0 & 0 \\<br />
{ – a \sin \psi \sin \theta } & { a \cos \psi \sin \theta } & 0 \\<br />
{ a \cos \psi \cos \theta } & { a \sin \psi \cos \theta } & { – a \sin \theta }<br />
\end{array} } \right | \; } \normalsize } \\ &<br />
= { { 2 a \cos \psi \sin \theta \cdot}\kern0pt { a \cos \psi \sin \theta \cdot \left ( { – a \sin \theta } \right ) } } \\ &<br />
= { – 2 { a ^ 3 } { \cos ^ 2 } \psi \, { \sin ^ 3 } \theta . }<br />
\end {align*} $$
این مقدار، متناظر با جهت رو به پایین سطح است.
انتگرال نخست، برابر است با:
I = ∬ S x d y d z = – 2 ∬ S a 3 cos 2 ψ sin 3 θ d ψ d θ = – 2 a 3 ∫ 0 2 π cos 2 ψ d ψ ∫ 0 π sin 3 θ d θ . \large \begin {align*} I & = \iint \limits _ S { x d y d z } = { – 2 \iint \limits _ S { { a ^ 3 } { { \cos } ^ 2 } \psi \, { { \sin } ^ 3 } \theta d \psi d \theta } } \\ & = { – 2 { a ^ 3 } \int \limits _ 0 ^ { 2 \pi } { { { \cos } ^ 2 } \psi d \psi } \int \limits _ 0 ^ \pi { { { \sin } ^ 3 } \theta d \theta } . } \end {align*} I = S ∬ x d y d z = –2 S ∬ a 3 cos 2 ψ sin 3 θ d ψ d θ = –2 a 3 0 ∫ 2 π cos 2 ψ d ψ 0 ∫ π sin 3 θ d θ .
دو انتگرال اخیر را به صورت جداگانه محاسبه میکنیم:
∫ 0 2 π cos 2 ψ d ψ = 1 2 ∫ 0 2 π ( 1 + cos 2 ψ ) d ψ = 1 2 [ ( ψ + sin 2 ψ 2 ) ∣ 0 2 π ] = π , ∫ 0 π sin 3 θ d θ = ∫ 0 π sin 2 θ sin θ d θ = ∫ 0 π ( cos 2 θ – 1 ) d ( cos θ ) = ( cos 3 θ 3 – cos θ ) ∣ 0 π = ( cos 3 π 3 – cos π ) – ( cos 3 0 3 – cos 0 ) = ( – 1 3 + 1 ) − ( 1 3 – 1 ) = 4 3 . \large \begin {align*} \int \limits _ 0 ^ { 2 \pi } { { { \cos } ^ 2 } \psi d \psi } & = { \frac { 1 } { 2 } \int \limits _ 0 ^ { 2 \pi } { \left ( { 1 + \cos 2 \psi } \right ) d \psi } } \\ & = { \frac { 1 } { 2 } \left [ { \left . { \left ( { \psi + \frac { { \sin 2 \psi } } { 2 } } \right ) } \right | _ 0 ^ { 2 \pi } } \right ] } = { \pi , } \\ \int \limits _ 0 ^ \pi { { { \sin } ^ 3 } \theta d \theta } & = { \int \limits _ 0 ^ \pi { { { \sin } ^ 2 } \theta \sin \theta d \theta } } = { \int \limits _ 0 ^ \pi { \left ( { { \cos ^ 2 } \theta – 1 } \right ) d \left ( { \cos \theta } \right ) } } \\ & = { \left . { \left ( { \frac { { { \cos ^ 3 } \theta } } { 3 } – \cos \theta } \right ) } \right | _ 0 ^ \pi } = { \left ( { \frac { { { \cos ^ 3 } \pi } } { 3 } – \cos \pi } \right ) – \left ( { \frac {{ { \cos ^ 3 } 0 } } { 3 } – \cos 0 } \right ) } \\ & = { \left ( { – \frac { 1 } { 3 } + 1 } \right ) } - { \left ( { \frac { 1 } { 3 } – 1 } \right ) } = { \frac { 4 } { 3 } . } \end {align*} 0 ∫ 2 π cos 2 ψ d ψ 0 ∫ π sin 3 θ d θ = 2 1 0 ∫ 2 π ( 1 + cos 2 ψ ) d ψ = 2 1 ( ψ + 2 sin 2 ψ ) 0 2 π = π , = 0 ∫ π sin 2 θ sin θ d θ = 0 ∫ π ( cos 2 θ –1 ) d ( cos θ ) = ( 3 cos 3 θ – cos θ ) 0 π = ( 3 cos 3 π – cos π ) – ( 3 cos 3 0 – cos 0 ) = ( – 3 1 + 1 ) − ( 3 1 –1 ) = 3 4 .
در نتیجه، مقدار انتگرال سطحی به صورت زیر محاسبه میشود:
I = – 2 a 3 ⋅ π ⋅ 4 3 = – 8 a 3 π 3 . \large { I = – 2 { a ^ 3 } \cdot \pi \cdot \frac { 4 } { 3 } } = { – \frac { { 8 { a ^ 3 } \pi } } { 3 } . } I = –2 a 3 ⋅ π ⋅ 3 4 = – 3 8 a 3 π .
اگر مطلب بالای برای شما مفید بوده است و علاقهمند به یادگیری مباحث مشابه آن هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش انتگرال سطحی میدان برداری – به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی پارامترهکردن سطح در انتگرال سطح برداری فیلم آموزشی انتگرال سطح میدان برداری فیلم آموزشی حل چند مثال از انتگرال سطح میدان برداری