اسیلاتور پل وین — به زبان ساده (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس، درباره انواع اسیلاتورها بحث کردیم. در این آموزش قصد داریم اسیلاتور پل وین را بررسی کنیم. این اسیلاتور برای تولید نوسان‌های سینوسی از دو شبکه RC متصل به هم استفاده می‌کند. در مبحث مربوط به اسیلاتورهای RC، دیدیم که با اتصال یک تقویت‌کننده معکوس‌کننده به شبکه مقاومتی-خازنی، می‌توان یک مدار اسیلاتور یا نوسان‌ساز ساخت. اسیلاتور پل وین نیز از همین حقیقت برای تولید نوسان‌های سینوسی استفاده می‌کند.

اساس کار اسیلاتور پل وین

یکی از ساده‌ترین انواع اسیلاتورهای موج سینوسی، «اسیلاتور پل وین» (The Wien Bridge Oscillator) نام دارد. در این اسیلاتور به جای مدار تانک تنظیم‌شده LC از شبکه RC برای تولید شکل موج سینوسی در خروجی استفاده می‌شود.

فیلم آموزش الکترونیک ۳ – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

اسیلاتور پل وین، بر اساس «مدار پل وتستون» (Wheatstone bridge circuit) ساخته می‌شود و دلیل نامگذاری آن نیز همین موضوع است. مدار اسیلاتور پل وین، یک تقویت‌کننده دارد که با شبکه RC دو طبقه تزویج می‌شود. پایداری فرکانسی مناسب در فرکانس تشدید، تنظیم ساده و اعوجاج کم، از ویژگی‌های این شبکه RC دوطبقه است. به علت وجود این ویژگی‌ها، از اسیلاتور پل وین در دستگاه‌های تولیدکننده صدا استفاده می‌شود. فرکانس موج سینوسی تولید شده توسط این دستگاه‌ها، در محدوده شنوایی انسان و بین ۱۶ هرتز تا ۲۰ کیلوهرتز است. ذکر این نکته ضروری است که اختلاف فاز بین سیگنال‌های خروجی و ورودی در اسیلاتورهای پل ویِن، با اسیلاتورهای RC بسیار متفاوت است.

فیدبک اسیلاتور پل وین، شامل یک مدار RC سری و یک مدار RC موازی با مشخصات مشابه است. به این ترتیب، بسته به فرکانس کاری در این مدار، تاخیر یا تقدم فاز روی می‌دهد. جابجایی فاز این شبکه RC در فرکانس تشدید ($$f_r$$) برابر صفر است.

شکل زیر، یک شبکه جابجایی فاز RC را نشان می‌دهد:

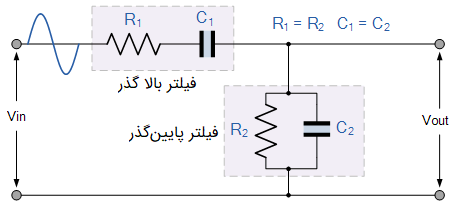
شبکه RC نشان داده شده در شکل بالا، شامل یک مدار RC سری و یک مدار RC موازی است. همانطور که مشاهده می‌شود، مدار RC موازی همانند فیلتر پایین‌گذر و مدار RC سری همانند فیلتر بالاگذر عمل می‌کند. به این ترتیب، یک فیلتر میان‌گذر درجه دوم وابسته به فرکانس خواهیم داشت. این فیلتر میان‌گذر در فرکانس تشدید ($$f_r$$)، «ضریب کیفیت» (Quality Factor) بالایی دارد.

فرکانس نوسان اسیلاتور پل وین

در فرکانس‌های پایین، خازن سری ($$C_1$$) راکتانس بسیار بزرگی دارد و مانند مدار باز عمل می‌کند. به این ترتیب، این خازن هر نوع سیگنال ورودی ($$V_{in}$$) را حذف یا «بلوکه» (Block) می‌کند و خروجی مدار ($$V_{out}$$) صفر می‌شود.

فیلم آموزش الکترونیک ۳ – مرور و حل مساله در فرادرس

کلیک کنید

به طور مشابه در فرکانس‌های بالا،‌ راکتانس خازن موازی ($$C_2$$) بسیار کوچک است و خازن مانند اتصال کوتاه عمل می‌کند. بنابراین باز هم خروجی مدار ($$V_{out}$$) صفر می‌شود.

در یک نقطه فرکانسی بین این دو اکسترمم (خازن $$C_1$$ مدار باز و خازن $$C_2$$ اتصال کوتاه)، ولتاژ خروجی ($$V_{out}$$) به حداکثر مقدار خود می‌رسد. فرکانس سیگنال ورودی که در آن، ولتاژ خروجی حداکثر می‌شود، فرکانس تشدید اسیلاتور ($$f_r$$) نام دارد.

در فرکانس تشدید، راکتانس مدار با مقدار مقاومت آن برابر می‌شود. یعنی داریم:

$$X_C = R$$

همچنین در فرکانس تشدید، اختلاف فاز سیگنال‌های ورودی و خروجی برابر صفر است. بنابراین دامنه ولتاژ خروجی در حداکثر مقدار ممکن خود و برابر با یک سوم دامنه ولتاژ ورودی است. این مسئله در شکل زیر نشان داده شده است:

همانطور که در شکل (۲) مشاهده می‌شود،‌ اختلاف فاز بین سیگنال‌های ورودی و خروجی در فرکانس‌های پایین مثبت است. در این حالت، «تقدم فاز» (Phase Lead) به وجود می‌آید. در حالی که در فرکانس‌های بالا، این اختلاف فاز منفی است. در این حالت، «تأخیر فاز» (Phase Lag) به وجود می‌آید. در یک نقطه بین این دو وضعیت، مدار به فرکانس تشدید خود می‌رسد. در این حالت، دو سیگنال ورودی و خروجی «هم‌فاز» (In-Phase) می‌شوند و اختلاف فاز بین آنها برابر صفر درجه خواهد شد. بنابراین می‌توان فرکانس تشدید را به وسیله رابطه زیر تعریف کرد:

$$f_r = \frac{1}{2 \pi RC}$$

که در آن:

• $$f_r$$ فرکانس تشدید با واحد هرتز است.
• $$R$$ مقاومت با واحد اهم است.
• $$C$$ مقدار ظرفیت خازن با واحد فاراد است.

پیش از این گفتیم که دامنه ولتاژ خروجی ($$V_{out}$$) در فرکانس تشدید حداکثر مقدار ممکن خود را دارد و برابر با یک سوم دامنه ولتاژ ورودی ($$V_{in}$$) است. این دامنه، به نوعی شرط نوسان مدار نیز هست. اما علت اینکه این مقدار، یک سوم مقدار ولتاژ ورودی است و مشابه مقدار ولتاژ ورودی نیست، در ادامه بیان می‌شود. برای درک این مطلب، لازم است امپدانس مختلط ($$Z =R \pm jX$$) دو مدار متصل RC را در نظر بگیریم.

بر اساس تئوری موج‌های سینوسی متناوب یا AC، می‌دانیم که قسمت حقیقی امپدانس مختلط، مقاومت ($$R$$) و قسمت موهومی آن، راکتانس $$X$$ است. مدار اسیلاتور پل وین فقط شامل خازن است و سلف ندارد. بنابراین راکتانس امپدانس مختلط با راکتانس خازنی مدار ($$X_C$$) یکسان است.

شبکه RC در اسیلاتور پل وین

شکل زیر، شبکه RC در اسیلاتور پل وین را نشان می‌دهد:

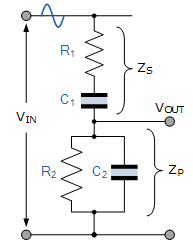
مطابق شکل، این شبکه شامل دو مدار RC متصل به هم است و خروجی اسیلاتور نیز از محل اتصال این دو مدار گرفته می‌شود. ترکیب سری بالایی شامل مقاومت $$R_1$$ و خازن $$C_1$$، و ترکیب موازی پایینی شامل مقاومت $$R_2$$ و خازن $$C_2$$ است. امپدانس DC‌ قسمت بالایی مدار یا شبکه سری ($$R_1 C_1$$) با $$Z_s$$ و همچنین امپدانس کلی قسمت پایینی مدار یا شبکه موازی ($$R_2 C_2$$) با $$Z_p$$ نشان داده می‌شود. دو امپدانس سری $$Z_p$$ و $$Z_s$$ به ورودی مدار ($$V_{in}$$) متصل هستند. مطابق شکل (۳)، خروجی اسیلاتور از دو سر امپدانس $$Z_p$$ گرفته می‌شود. بنابراین یک شبکه تقسیم‌کننده ولتاژ حاصل می‌شود. حال فرض کنید که مقدار مقاومت‌های $$R_1$$ و $$R_2$$ برابر $$12k \Omega$$ و ظرفیت خازن‌های $$C_1$$ و $$C_2$$ برابر $$3.9 nF$$ و فرکانس منبع $$3.4kHz$$ باشد.

مدار سری شبکه RC

امپدانس کلی ترکیب سری با مقاومت $$R_1$$ و خازن $$C_1$$، به صورت زیر محاسبه می‌شود:

$$R=12k \Omega \, \, \, , \, \, \, X_C = \frac{1}{2 \pi f C}$$

$$X_C = \frac{1}{2 \pi \times 3.4 kHz \times 3.9 nF} = 12k \Omega$$

$$Z_s = \sqrt{R^2 + X_C^2} = \sqrt{12000^2 + 12000^2}$$

$$Z_s = 16970 \Omega \approx 17 k \Omega$$

بنابراین اگر فرکانس منبع تغذیه برابر با $$3.4kHz$$ باشد، راکتانس خازن و مقاومت مدار برابر $$12k \Omega$$ و امپدانس سری $$Z_s$$ برابر $$17 k\Omega$$ می‌شود. نحوه محاسبه امپدانس $$Z_p$$ پایینی، متفاوت است زیرا مقاومت و خازن تشکیل‌دهنده این مدار موازی هستند.

مدار موازی شبکه RC

امپدانس کلی برای ترکیب موازی پایینی با مقاومت $$R_2$$ و خازن $$C_2$$ به صورت زیر داده می‌شود:

$$R= 12 k \Omega \, \, \, , \, \, \, X_c = 12 k \Omega$$

$$\frac{1}{Z} = \frac{1}{R} + \frac{1}{XC} = \frac{1}{12000} + \frac{1}{12000}$$

$$Z= 6000 \Omega = 6 k \Omega$$

امپدانس DC مدار موازی RC، در فرکانس سیگنال ورودی برابر با $$6 k \Omega$$ است. بردار جمع امپدانس موازی، به صورت زیر محاسبه می‌شود:

$$R = 6 k \Omega \, \, \, , \, \, \, X_c = 6 k \Omega$$

$$Z_p = \sqrt{R^2 + X_c^2} = \sqrt{6000^2 + 6000^2}$$

$$\to Z_p = 8485 \Omega \approx 8.5 k \Omega$$

حال اندازه بردار امپدانس سری ($$Z_s$$) و امپدانس موازی ($$Z_p$$) را داریم. بنابراین، کل امپدانس مشاهده شده در خروجی اسیلاتور ($$Z_{out}$$) در فرکانس داده شده عبارت است از:

$$Z_{out} = \frac{Z_p}{Z_p + Z_s} = \frac{8.5k \Omega}{8.5 k \Omega + 17 k \Omega}= 0.333 = \frac{1}{3}$$

در فرکانس نوسان، دامنه ولتاژ خروجی ($$V_{out}$$) با حاصل ضرب $$Z_{out}$$ در $$V_{in}$$ برابر است. پس می‌توان نتیجه گرفت که دامنه ولتاژ خروجی در این شبکه RC، برابر با یک سوم دامنه ولتاژ ورودی $$V_{in}$$ است.

این شبکه RC، مانند یک فیلتر میان‌‌گذر عمل می‌کند و «انتخاب‌گر فرکانس» (Frequency Selective) است و اساس کار مدار اسیلاتور پل وین را تشکیل می‌دهد.

مدار ساده اسیلاتور پل وین

حال اگر این شبکه RC را به یک تقویت‌کننده معکوس‌کننده با بهره $$1+\frac{R_1}{R_2}$$ متصل کنیم، مدار اسیلاتور پل وین به صورت شکل زیر در می‌آید:

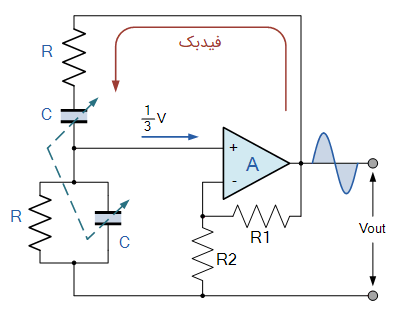
فیدبک در اسیلاتور پل وین، از خروجی تقویت‌کننده به هر دو ورودی آن متصل می‌شود. یک قسمت از این فیدبک که به ورودی با پلاریته منفی تقویت‌کننده متصل شده است به نام فیدبک منفی یا فیدبک دژنراتیو (Degenerative Feedback) شناخته می‌شود. این قسمت فیدبک، شامل یک شبکه تقسیم‌کننده مقاومتی با مقاومت‌های $$R_1$$ و $$R_2$$ است. به این ترتیب، بهره ولتاژ تقویت‌کننده محدود و تنظیم می‌شود. قسمت دیگری از شبکه فیدبک، به ورودی با پلاریته مثبت تقویت‌کننده متصل است. این قسمت فیدبک، شامل ترکیب سری خازن $$C$$ و مقاومت $$R$$ است که به آن فیدبک مثبت یا «فیدبک بازتولیدی» (Regenerative Feedback) گویند.

فیلم آموزش الکترونیک ۲ – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

این فیدبک‌های مثبت و منفی، باعث نوسان اسیلاتور می‌شوند. همانطور که در شکل (۳) مشاهده می‌شود، مسیر مثبت فیدبک در تقویت‌کننده پل وین به یک شبکه RC متصل است. این شبکه در فرکانس تشدید ($$f_r$$)، جابجایی فاز معادل صفر خواهد داشت و ولتاژ اعمال شده به پایانه‌های مثبت و منفی تقویت‌کننده با هم برابر و هم‌فاز می‌شوند. بنابراین سیگنال فیدبک مثبت اثر فیدبک منفی را خنثی می‌کند و باعث می‌شود که مدار خاصیت نوسانی پیدا کند.

برای آنکه اسیلاتور شروع به نوسان کند، بهره ولتاژ مدار تقویت‌کننده باید برابر یا بزرگتر از سه باشد. زیرا همانطور که گفتیم، ولتاژ خروجی اسیلاتور پل وین یک سوم ولتاژ ورودی آن است. این مقدار ($$A_v \geq 3$$) به وسیله شبکه مقاومتی فیدبک ($$R_1$$ و $$R_2$$) تنظیم می‌شود. برای یک تقویت‌کننده غیر معکوس کننده بهره ولتاژ برابر با $$1+ \frac{R_1}{R_2}$$ است.

همچنین، به دلیل محدودیت‌های بهره حلقه باز در تقویت‌کننده‌های عملیاتی،‌ دست‌یابی به فرکانس‌های بالای $$1MHz$$ بدون استفاده از تقویت‌کننده‌های فرکانس بالا غیر ممکن خواهد بود.

در ادامه با بیان دو مثال، اسیلاتور پل وین را مورد بررسی بیشتر قرار می‌دهیم.

مثال ۱

در یک اسیلاتور پل وین مقدار مقاومت برابر $$10 k \Omega$$ است و خازن متغیر ظرفیتی در محدوده $$1nF$$ تا $$1000nF$$ دارد. حداکثر و حداقل مقدار فرکانس نوسان در این اسیلاتور را بیابید.

حل: رابطه فرکانس نوسان برای اسیلاتور پل وین به صورت زیر است:

$$f_r = \frac{1}{2 \pi RC}$$

حداقل فرکانس نوسان برای این اسیلاتور به صورت زیر محاسبه می‌شود:

$$f_{min} = \frac{1}{2 \pi (10 k\Omega)\times (1000 \times 10^ {-9})} = 15.9 Hz$$

به همین ترتیب، حداکثر فرکانس نوسان اسیلاتور پل وین به صورت زیر خواهد بود:

$$f_{max} = \frac{1}{2 \pi (10k\Omega)\times (1 \times 10^{-9})} = 15915Hz \approx 15 kHz$$

مثال ۲

یک اسیلاتور پل وین، در فرکانس ۵۲۰۰ هرتز یا $$5.2kHz$$، شکل موج سینوسی تولید می‌کند. مقادیر مقاومت‌های $$R_1$$ و $$R_2$$‌ و خازن‌های $$C_1$$ و $$C_2$$ را برای ایجاد نوسان در این اسیلاتور بیابید. مدار این اسیلاتور بر اساس تقویت‌کننده عملیاتی غیر معکوس‌کننده طراحی شده است. حداقل مقدار بهره را برای ایجاد نوسان‌ها در فرکانس نوسان اسیلاتور بیابید و در نهایت، مدار آن را رسم کنید.

حل: می‌دانیم فرکانس نوسان اسیلاتور به صورت زیر محاسبه می‌شود:

$$f_r = \frac{1}{2 \pi RC} = 5200 Hertz = 5.2 kHz$$

فرکانس نوسان اسیلاتور پل وین به اندازه ۵۲۰۰ هرتز داده شده است. اگر مقاومت‌های $$R_1$$ و $$R_2$$ و خازن‌های $$C_1$$ و $$C_2$$ با هم برابر باشند و همچنین ظرفیت خازن فیدبک برابر $$3nF$$ فرض شود،‌ مقدار مقاومت فیدبک به صورت زیر محاسبه می‌شود:‌

$$f_r = \frac{1}{ 2 \pi RC} \to R = \frac{1}{2 \pi f_r C}$$

$$R = \frac{1}{2 \pi \times 5200 \times 3.0 \times 10^{-9}} = 10200 \Omega = 102 k \Omega$$

شکل زیر،‌ مدار این اسیلاتور پل وین را نشان می‌دهد:

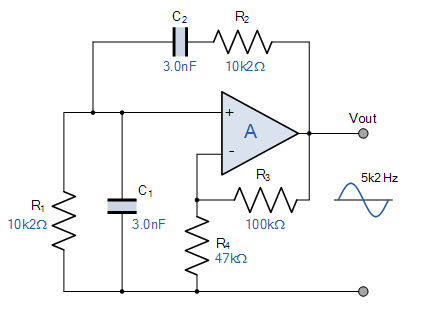
برای شروع نوسان‌ها، بهره ولتاژ در مدار اسیلاتور پل وین باید برابر یا بزرگتر از ۳ باشد ($$A_v \geq 3$$). برای یک اپ - امپ غیر معکوس‌کننده، این مقدار به وسیله شبکه مقاومتی ($$R_3$$ و $$R_4$$) و به صورت زیر تعیین می‌شود:

$$A_v = \frac{V_{out}}{V_{in}}= 1 + \frac{R_3}{R_4} =3$$

اگر مقدار مقاومت $$R_3$$ را برابر با $$100k \Omega$$ فرض کنیم، مقدار مقاومت $$R_4$$ به صورت زیر محاسبه می‌شود:

$$1+ \frac{R_3}{R_4} = 3$$

$$R_4 = \frac{R_3}{(3-1)} = \frac{R_3}{2}$$

$$R_3 = 100 k \Omega \to R_4 = 50 k\Omega$$

همانطور که گفتیم، حداقل بهره مدار باید سه باشد تا اسیلاتور شروع به نوسان کند. در عمل،‌ بهره ولتاژ مدار باید کمی بزرگتر از سه باشد. با فرض اینکه مقدار بهره برابر با ۳.۱ است، مقدار مقاومت $$R_4$$ برابر با $$47 k \Omega$$ می‌شود.

جمع‌بندی

شرایط لازم برای شروع نوسان‌ها در اسیلاتور پل وین به صورت زیر است:

• اگر سیگنال ورودی وجود نداشته باشد، اسیلاتور پل وین در خروجی خود سیگنال پیوسته نوسانی تولید می‌کند.
• اسیلاتور پل وین می‌تواند در بازه وسیعی از فرکانس، تولید موج نوسانی کند.
• بهره ولتاژ‌ تقویت‌کننده باید بزرگتر از سه باشد.
• در تقویت‌کننده غیر معکوس‌کننده از شبکه RC استفاده می‌شود.
• مقاومت ورودی تقویت‌کننده نسبت به مقاومت فیدبک ($$R$$) باید بزرگ باشد. به این ترتیب شبکه RC دچار اضافه بار نمی‌شود و شرایط لازم برای نوسان را تغییر نمی‌دهد.
• مقاومت خروجی تقویت‌کننده باید به اندازه کافی کم باشد تا اثر بار خارجی حداقل شود.
• باید روش‌هایی برای پایدار کردن دامنه نوسان‌ها در نظر گرفته شود. اگر بهره ولتاژ تقویت‌کننده خیلی کم باشد، نوسان‌ها ابتدا میرا می‌شوند و سپس از بین می‌روند. اگر این بهره خیلی بزرگ باشد، ولتاژ در خروجی تا حد ولتاژ منبع اشباع می‌شود و سیگنال خروجی اعوجاج می‌یابد.
• اگر در فیدبک اسیلاتور پل وین از دیود استفاده شود، دامنه نوسان‌ها پایدار می‌شود و نوسان تا بی‌نهایت ادامه پیدا می‌کند.

در بخش بعدی از این سری آموزش‌های مجله فرادرس، به بررسی اسیلاتورهای کریستالی می‌پردازیم. مدار تانک این اسیلاتورها از جنس کریستال کواترز است که در فرکانس‌های بالا تولید شکل موج سینوسی با دامنه پایدار می‌کند.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• اسیلاتور LC — به زبان ساده
• اسیلاتور هارتلی — به زبان ساده
• اسیلاتور کولپیتس — به زبان ساده

^^