استرین گیج (Strain Gauge) چیست؟ — از صفر تا صد

استرین گیج وسیلهای است که اگر در معرض مقداری نیرو قرار بگیرد، در مقاومت آن تغییر ایجاد میشود. تغییر در مقاومت یا بر اساس بار مکانیکی متصل به آن و یا بر اساس جابهجایی اندازهگیری میشود. در این مطلب قصد داریم به بررسی ساختار و اصول کار یک استرین گیج بپردازیم.
استرین گیج
استرین گیج در سال ۱۹۳۸ توسط دو دانشمند به نامهای «ادوارد سایمون» (Edward E Simmons) و «آرتور راگ» (Arthur C Ruge) اختراع شد. یک استرین گیج معمولا «کشش» (Strain) را با استفاده از «فشار» (Stress) اندازه میگیرد. استرین گیج به صورت مستقیم برای اندازهگیری بار و به صورت غیر مستقیم برای اندازهگیری جابهجایی مورد استفاده قرار میگیرد. این وسیله اندازهگیری به عنوان ترانسدیوسر ثانویه در بسیاری از آشکارسازها و ترانسدیوسرهایی مانند «لود سلها» (Load Cells)، «گشتاور سنجها» (Torque Meters)، «سنسورهای دما» (Temperature Sensors) و شتاب سنجها به کار گرفته میشود.
اصول کار استرین گیج
فرض کنید یک سیم در اختیار داریم که طول آن برابر با L و مساحت مقطع عرضی آن برابر با A است. این سیم اگر در معرض کشش یا فشرده شدن قرار بگیرد، مقاومت آن دچار تغییر میشود. این امر به دلیل تغییر در ابعاد سیم و یک مشخصه از مواد است که «اثر پیزو رزیستیو» (Piezo Resistive Effect) نام دارد. در تصویر زیر نمایی از تغییر در ابعاد یک استرین گیج بر اثر اعمال نیرو نشان داده شده است.
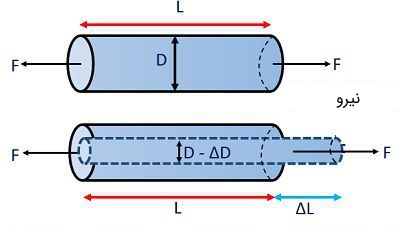
اثر پیزو رزیستیو بیان میکند که تغییر در ابعاد یک رسانا منجر به تغییر در مقاومت آن میشود. بر همین اساس، استرین گیجهای مقاومتی با نام گیجهای پیزو رزیستیو نیز شناخته میشوند. مقاومت یک ماده بر اساس رابطه زیر به دست می آید:
در این فرمول، مقاومت ویژه ماده، طول ماده و سطح مقطع آن است. با مشتق گرفتن از رابطه مقاومت فوق، به معادله زیر میرسیم:
کشش محوری با رابطه زیر مشخص میشود:
کشش مقطعی نیز بر اساس رابطه زیر به دست میآید:
نرخ پواسون که برابر با نسبت کشش مقطعی به کشش محوری است، به صورت زیر محاسبه خواهد شد:
از قبل میدانیم که حجم سیم بر اساس رابطه زیر به دست میآید:
با مشتق گرفتن از رابطه حجم به معادله زیر میرسیم:
با استفاده از روابط قبلی، این معادله را میتوان به فرم زیر بازنویسی کرد:
چون است، بنابراین داریم:
همان طور که میدانیم:
حال اگر مقدار را در این معادله جایگذاری کنیم، داریم:
حال اگر معادله فوق را بر تقسیم کنیم:
نتیجهای که پس از سادهسازی به دست میآید به صورت زیر است:
در نهایت «پارامتر گَیج» (Gauge Factor) برابر است با:
در این رابطه، برابر با تغییر در مقاومت به دلیل تغییر در طول، تغییر در مقاومت به دلیل تغییر در مساحت و تغییر در مقاومت به دلیل اثر پیزو رزیستیو است. زمانی که از تغییر در مقاومت به دلیل اثر پیزو رزیستیو صرف نظر کنیم، معادله به فرم زیر سادهسازی میشود:
البته توجه کنید که معادله فوق فقط زمانی صادق است که اثر پیزو رزیستیو تقریبا قابل صرف نظر باشد. مقدار نرخ پواسون برای تمام فلزات بین ۰ تا ۰٫۵ است که منجر به پارامتر گیج تقریبا برابر با ۲ میشود.
انواع استرین گیج
استرین گیجها انواع مختلفی دارند و عموما آنها را به گروههای زیر طبقه بندی میکنند.
استرین گیج فلزی نامحدود
«استرین گیج فلزی نامحدود» (Unbounded Metal Strain Gauge) یک نوع استرین گیج است که در آن یک قطعه سیم در یک واسط عایقبندی شده بین دو نقطه مورد کشش واقع میشود. واسط عایقبندی شده میتواند هوا باشد. همچنین جنس سیم میتواند از آلیاژهایی مانند نیکل مس، نیکل کروم و نیکل آهن و با قطر حدود ۰٫۰۰۳ میلی متر باشد. پارامتر گیج برای این گروه از استرین گیجها در حدود ۲ تا ۴ است و میتواند نیرویی برابر با ۲ میلی نیوتون را تحمل کند. این نوع از استرین گیجها به صورت انحصاری در کاربردهای ترانسدیوسر مورد استفاده قرار میگیرند که در آنها سیمهای با مقاومت پیش بارگذاری شده در یک پیکربندی پل وتسون متصل شدهاند.
استرین گیج سیمی محدود
در ساختار ترانسدیوسرها، از یک «استرین گیج سیمی محدود» (Bonded Wire Strain Gauge) برای آنالیز تنش استفاده میشود. یک استرین گیج سیمی مقاومتی، از یک سیم با قطر ۰٫۲۵ میلی متر یا کمتر تشکیل شده است. «شبکه سیمی مقاومتی» (Grid of Resistance Wire) به یک حامل محکم متصل شده است که میتواند یک صفحه نازک کاغذ و یا یک صفحه تفلون باشد. در تصویر زیر نمایی از یک استرین گیج سیمی محدود نشان داده شده است.
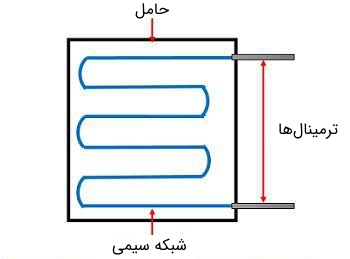
برای جلوگیری از آسیب دیدن مکانیکی سیمها، روی آنها با یک صفحه نازک فلزی پوشانده شده است. گسترده شدن سیمها در یک صفحه باعث میشود که توزیع یکنواختی از تنش در سرتاسر شبکه به دست آید. حامل به وسیله یک ماده چسبناک به صورت محکمی به جسم مورد اندازهگیری میچسبد. به همین دلیل تبادل کشش بسیار خوبی از حامل به صفحه سیمی انجام میگیرد. یک استرین گیج سیمی مقاومتی برای اینکه دارای عملکرد مطلوب باشد، باید مشخصههای زیر را در خود داشته باشد:
- استرین گیج باید پارامتر گیج با مقادیر بزرگی داشته باشد؛ زیرا پارامتر گیج بزرگ نشان دهنده تغییرات بزرگ در مقاومت است که منجر به حساسیت بالا میشود.
- مقاومت گیج باید بالا باشد تا از اثر تغییرات نامطلوب مقاومت در مدار اندازهگیری کاسته شود. معمولا مقدار مقاومت استرین گیج ۱۲۰، ۳۵۰ یا ۱۰۰۰ اهم است. البته مقدار مقاومت بزرگ منجر به حساسیت کمتر میشود. بنابراین برای داشتن حساسیت بالا، باید از ولتاژ پل بزرگتری استفاده شود.
- یک استرین گیج باید دارای ضریب حرارتی مقاومت پایینی باشد.
- استرین گیج باید منحنی مشخصه خطی داشته باشد تا در تمام طول بازه خود از ثبات کالیبراسیون برخوردار باشد.
- استرین گیج باید دارای پاسخ فرکانسی خوبی باشد و خطی بودن باید در تمام محدوده دقت حفظ شود.
استرین گیج فویل فلزی محدود
این گروه از استرین گیجها یک نوع توسعه یافته از استرین گیجهای سیمی محدود قبلی به شمار میآیند. استرین گیج فویل فلزی محدود از مواد مشابه با استرین گیجهای سیمی محدود استفاده میکند. کاربرد اصلی این نوع از استرین گیجها در آنالیز تنش و نیز بسیاری از انواع ترانسدیوسرها است. در تصویر زیر نمایی از یک استرین گیج فویل فلزی محدود نشان داده شده است.
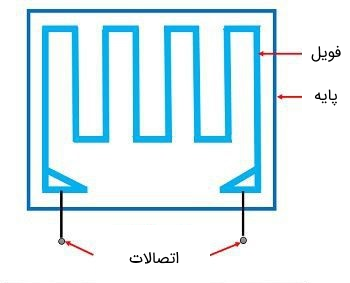
استرین گیجهای نوع فویلی بازه دما عملکرد بالاتری دارند. دلیل این ویژگی این است که در مقایسه با استرین گیج نوع سیمی محدود از توانایی اتلاف حرارتی بالاتری برخوردار هستند؛ زیرا به ازای حجم برابر، دارای ناحیه سطح بزرگتری هستند. داشتن ناحیه سطح بزرگتر منجر به پیوند بهتر میشود.
استرین گیج نیمه هادی
عملکرد یک استرین گیج نیمه هادی به اثر پیزو رزیستیو بستگی دارد. به عبارت دیگر، تغییر در مقاومت ویژه باعث تغییر در مقاومت کلی میشود. این نوع از استرین گیجٰها اساسا در شرایطی مورد استفاده قرار میگیرند که پارامتر گیج بزرگ و پوشهای کوچک مورد نیاز باشند. مقاومت نیمه هادی متناسب با کشش اعمال شده به استرین گیج تغییر میکند. در تصویر زیر نمایی از استرین گیج نوع نیمه هادی و اجزای مختلف آن نشان داده شده است.
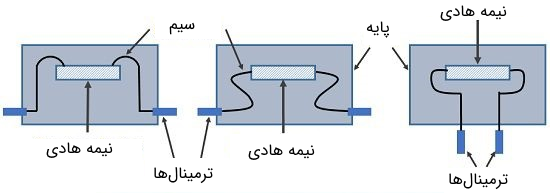
همان طور که از نام این استرین گیجها نیز مشخص است، در ساختار آنها از مواد نیمه هادی مانند سیلیکون و ژرمانیوم استفاده شده است. استرین گیجهای معمولی دارای یک ماده کریستالی در ساختار خود هستند که حساس به کشش است و در طول پایهها به صورت محافظتی قرار گرفته است. استرین گیجهای نیمه هادی دارای مزایای زیر هستند:
- این نوع از استرین گیجها دارای پارامتر گیج بالاتری در حدود هستند.
- استرین گیج نوع نیمه هادی از مشخصه هیسترزیس مربوط به نیمه هادیها برخوردار است.
- استرین گیجهای نوع نیمه هادی طولهای بسیاری کوچکی در بازه ۰٫۷ تا ۷ میلی متر دارند.
- این نوع از استرین گیجها در اندازهگیری کشش محلی بسیار مفید هستند.
استرین گیجهای نیمه هادی معایبی نیز دارند که از جمله آنها میتوان به موارد زیر اشاره کرد:
- یکی از مهمترین معایب این نوع از استرین گیجها این است که نسبت به تغییرات دمایی بسیار حساس هستند.
- خطی بودن پاسخ در استرین گیج نیمه هادی بسیار کم و ضعیف است.
استرین گیج پخش شده (Diffused)
این گروه از استرین گیجها معمولا در ترانسدیوسرها مورد استفاده قرار میگیرند و در آنها فرایند دیفیوژن اعمال شده است که در تکنولوژی ساخت IC مورد استفاده قرار گرفته است. در ترانسدیوسرهای فشار، از این نوع استرین گیجها به عنوان المان اندازهگیری استفاده میشود.
جبرانسازی حرارتی استرین گیج
در تصویر زیر نمایی از یک مدار جبرانساز حرارتی برای استرین گیجها نشان داده شده است.
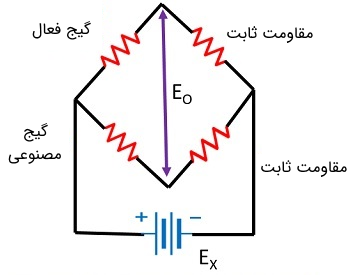
در مدار فوق، «گیج فعال» (Active Gauge) در معرض کشش قرار گرفته است، در حالی که کشش به «گیج مصنوعی» (Dummy Gauge) اعمال نمیشود. دمای هر دو گیج فعال و گیج مصنوعی باید ثابت نگه داشته شود. تغییر در مقاومت همواره از طریق پل وتسون اندازهگیری میشود. در واقع دو نوع مدار برای اندازهگیری وجود دارند که در یکی از آنها از «پل متعادل» (Balanced Bridge) استفاده میشود و در نوع دیگر «پل نامتعادل» (Unbalanced Bridge) به کار گرفته میشود. در تصویر زیر یک مدار پل متعادل را میتوان مشاهده کرد.
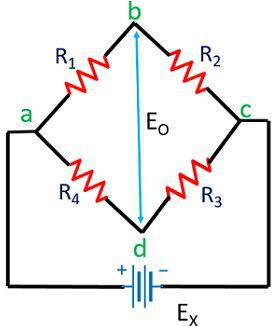
برای اینکه یک پل در حالت متعادل قرار داشته باشد، نقاط b و d باید دارای پتانسیل برابر باشند. به همین دلیل داریم:
معادلات فوق را بر یکدیگر تقسیم میکنیم:
در حالتی که هیچ جریانی از آشکارساز عبور نکند، معادلات زیر صادق هستند:
بنابراین معادلات قبل را میتوان به صورت زیر بازنویسی کرد:
اگر مقدار مقاومت را برابر با فرض کنیم، در این صورت میتوانیم بنویسیم:
این معادله بدین معنی است که هم از مقاومت و هم از مقاومت میتوان برای جبران حرارت استفاده کرد. به این مدار، «جبرانساز حرارتی محیط» (Ambient Temperature Compensation) گفته میشود.
کاربردهای استرین گیج
از استرین گیج در کاربردهای متنوعی استفاده میشود که از آن جمله میتوان به موارد زیر اشاره کرد:
- تعیین تنش تولید شده به وسیله ماشین آلات.
- تست قطعات و المانهای مختلف.
- در مهندسی خاک برای حفظ ریلها در شرایط صحیح و مناسب.
- در اندازهگیری گشتاور روی موتور از طریق اتصال یک استرین گیج به آن.
- در اندازهگیری کشش و تنش ناشی از آن در آنالیز تنش تجربی.
همان طور که میدانیم، پارامتر گیج برابر با نسبت تغییرات جزئی در مقاومت به تغییر در طول است. بنابراین برای یک استرین گیج فلزی، پارامتر گیج همواره برابر با ۲ است.













سلام رفرنس این مطالب رو از کجا میتونم پیدا کنم که برای پایان نامه معتبر باشه
با سلام؛
برای استفاده از مطالب مجله فرادرس میتوانید به «شرایط استفاده» در انتهای صفحه یا این لینک مراجعه کنید. همچنین، منبع تمامی مطالب مجله فرادرس اگر ترجمه باشند در انتهای مطلب و پیش از نام نویسنده آورده شدهاند.
با تشکر از همراهی شما با مجله فرادرس
رابطه پواسون یک منفی دارد
با سلام و وقت بخیر؛
فرمول اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.