آجر اویلر – به زبان ساده

در مطالب گذشته وبلاگ فرادرس در مورد اعداد حقیقی، اول و گنگ صحبت کردیم. از این رو در این مطلب قصد داریم تا مفهومی هندسی را توضیح دهیم که در آن از اعداد اول بهره گرفته شده است. در حقیقت ابعاد یک معکب می‌توانند کسری، گنگ یا اعدادی طبیعی باشند. شاید از نظر کاربرد‌های مهندسی یا فیزیکی مکعبی مناسب باشد که طول ابعاد آن اعداد طبیعی باشند. باید بگوییم چنین معکبی وجود دارد و به آجر اویلر معروف است.

آجر اویلر

در ریاضیات، آجر اویلر یا مکعب اویلر که به‌نام لئونارد اویلر نامگذاری شده است، مکعبی است که لبه‌ها و تمامی قطر‌های آن اعدادی طبیعی هستند.

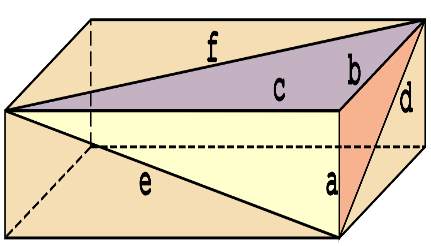
آجر اصلی اویلر نیز به مکعبی گفته می‌شود که طول‌های آن نسبت به هم اول باشند. در شکل زیر لبه‌های و قطر‌های وجوه نشان داده شده‌اند. تمامی این طول‌ها، مقادیری طبیعی هستند.

تعریف

ابعاد یک آجر اویلر را می‌توان مطابق با پاسخ معادله سیاله زیر در نظر گرفت.

$${ \color {white} { b ^ { 2 } +c ^ { 2 } = f ^{ 2 } } } { \begin {cases} a ^ { 2 } + b ^ { 2 }= d ^ { 2} \\ a ^ { 2} + c ^ { 2 } = e ^ { 2 } \\ b ^ { 2 } +c ^ { 2 } = f ^{ 2 } \end {cases}} { \color {white} { b ^ { 2 } +c ^ { 2 } = f ^{ 2 } } }$$

در رابطه فوق $$a , b , c$$ برابر با طول لبه‌ها بوده و $$d , e , f$$ نشان‌دهنده قطر‌ها هستند. این مکعب‌ها ویژگی‌هایی خاص داشته از این رو از آن در علوم و مهندسی استفاده می‌شود. در ادامه مهمترین ویژگی‌های این مکعب‌ها ارائه شده‌اند.

• اگر $$( a , b , c )$$ یکی از پاسخ‌های معادله فوق باشد در این صورت $$( k a , k b , k c )$$ نیز به عنوان یکی از پاسخ‌ها، مکعب اویلر محسوب می‌شود.
• اگر $$( a , b , c )$$ یکی از پاسخ‌های معادله فوق باشد در این صورت $$( b c , a c , a b )$$ نیز به عنوان یکی از پاسخ‌ها، مکعبی اویلری را نشان می‌دهد.
• حداقل دو لبه از آجر اویلر به $$3$$ بخش‌پذیر است.
• حداقل دو لبه از آجر اویلر به $$4$$ بخش‌پذیر است.
• حداقل یک لبه از آجر اویلر به $$11$$ بخش‌پذیر است.

نمونه‌هایی از آجر اویلر

کوچک‌ترین آجر اویلر در سال ۱۷۱۹ توسط «پاول هالک» (Paul Halcke) بدست آمد. لبه‌های این آجر برابر است با:

$$( d , e , f ) = ( 1 2 5 , 2 4 4, 267 )$$

در ادامه برخی دیگر از مهم‌ترین ابعاد یافته شده به عنوان آجر اویلر نیز ارائه شده‌اند.

$${ \color {white} { b ^ { 2 } +c ^ { 2 } = f ^{ 2 } } } \begin {align*} ( 85, 132, 720 ) & — ( 157, 725, 732 ) \\ ( 140, 480, 693 ) & — ( 500, 707, 843 ) \\ ( 160, 231, 792 ) & — ( 281, 808, 825 ) \\ ( 187, 1020, 1584 ) & — ( 1037, 1595, 1884 ) \\ ( 195, 748, 6336 ) & — ( 773, 6339, 6380 ) \\ ( 240, 252, 275 ) & — ( 348, 365, 373 ) \\ ( 429, 880, 2340 ) & — ( 979, 2379, 2500 ) \\ ( 495, 4888, 8160 ) & — ( 4913, 8175, 9512 ) \\ ( 528, 5796, 6325 ) & — ( 5820, 6347, 8579 ) \end {align*} { \color {white} { b ^ { 2 } +c ^ { 2 } = f ^{ 2 } } }$$

فرمول آجر اویلر

اویلر حداقل دو رابطه پارامتری را برای بدست آوردن چنین آجری اثبات کرد. البته هیچ‌یک از این دو رابطه نمی‌توانند تمامی پاسخ‌های ممکن را ارائه دهند. به‌منظور بدست آوردن رابطه در ابتدا $$( u , v , w )$$ را به‌عنوان طول‌های یک مثلث قائم‌الزاویه در نظر بگیرید که در رابطه فیثاغورث نیز برقرار هستند ($$u ^ 2 + v ^ 2 = w ^ 2$$). در این صورت اندازه لبه‌ها را می‌توان مطابق با رابطه زیر بدست آورد.

$$a = u | 4 v ^ { 2 } - w ^ { 2 } | \quad , \quad b = v | 4 u ^ { 2 } -w ^ { 2 } | \quad , \quad c = 4 u v w$$

هم‌چنین قطر‌های هر وجه نیز مطابق با روابط زیر قابل محاسبه هستند.

$$d = w ^ { 3 } \quad , \quad e = u ( 4 v^ { 2 }+ w ^ { 2 } ) \quad ,\quad f = v ( 4 u ^ { 2 } + w ^{ 2 } )$$

البته توجه داشته باشید که الزاما هر آجر اویلر در رابطه فوق ممکن است قرار نگیرد. برای نمونه آجری با ابعاد $$( a , b , c ) = ( 2 4 0 , 2 5 2 , 2 7 5 )$$ و قطر‌های وجه $$(d, e, f ) = ( 348 , 365 , 373 )$$ در روابط فوق قرار نمی‌گیرند.

آجر کامل

یک آجر کامل، مکعبی اویلری محسوب می‌شود که قطر فضایی آن نیز عددی صحیح است. به عبارتی دیگر معادله زیر نیز باید بین ابعاد اصلی (یا همان لبه‌ها) برقرار باشد. قطر فضایی، قطری است که دو گوشه مخالف مکعب را به هم وصل می‌کند.

$$\color {white} {a ^ { 2 } + b ^ { 2 } + c ^ { 2 } = g ^ { 2 } } { \displaystyle a ^ { 2 } + b ^ { 2 } + c ^ { 2 } = g ^ { 2 } } \color {white} {a ^ { 2 } + b ^ { 2 } + c ^ { 2 } = g ^ { 2 } }$$

در رابطه فوق $$g$$ نشان‌دهنده قطر فضایی است. تاکنون کسی مکعبی کامل را پیدا نکرده و هیچکس نیز هنوز وجود نداشتن مکعب کامل را اثبات نکرده است.

تحلیل‌های دقیق رایانه‌ای نشان می‌دهد که اگر یک آجر کامل وجود داشته باشد، در این صورت دو مورد زیر درباره آن صادق هستند.

• لبه فرد باید بیشتر از $$2 . 5 × 10 ^ { 13 }$$ باشد.
• کوتاه‌ترین طول نیز باید بیشتر از $$5 × 1 0 ^ {1 1 }$$ باشد.

آجر اصلی کامل یا آجر اولیه کامل نیز به مکعبی گفته می‌شود که هم لبه‌ها و قطر‌های وجوه آن، اعدادی صحیح بوده و همزمان نسبت به هم اعدادی اول باشند. در صورت وجود داشتن چنین مکعب‌هایی برخی از ویژگی‌ها نیز در مورد آن‌ها شناسایی شده که در ادامه ذکر شده‌اند.

• یکی از لبه‌ها، دو قطر وجه و قطر اصلی مکعب باید اعدادی فرد باشند. از طرفی یکی از لبه‌ها و دیگر قطر‌های وجوه باید به عدد $$4$$ تقسیم‌پذیر باشند. هم‌چنین دیگر لبه‌ها باید به عدد $$16$$ تقسیم‌پذیر باشند.
• طول یکی از لبه‌ها باید به عدد $$5$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها باید به عدد $$7$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها باید به عدد $$11$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها باید به عدد $$19$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها یا قطر فضایی باید به عدد $$13$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها، قطر وجه یا قطر فضایی باید به عدد $$17$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها، قطر وجه یا قطر فضایی باید به $$29$$ بخش‌پذیر باشد.
• طول یکی از لبه‌ها، قطر وجه یا قطر فضایی باید به $$37$$ بخش‌پذیر باشد.

آجر تقریبا کامل

یک مکعب تقریبا کامل، از 7 طول، دارای 6 طول صحیح است. چنین مکعب‌هایی را می‌توان در سه دسته حجمی، طولی یا سطحی تقسیم‌بندی کرد. در مورد مکعب حجمی، طول قطر فضایی عددی گنگ است. در مکعب طولی نیز یکی از لبه‌های $$a ، b ، c$$ عددی گنگ خواهد بود.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و هندسه، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• قضیه تالس -- به زبان ساده
• بردار و اسکالر — به زبان ساده
• قانون سینوس‌‌ها (Law of Sines) — به زبان ساده

^^