مرتب سازی هرمی (Heap Sort) – به زبان ساده
«مرتب سازی هرمی» (Heap Sort) یک الگوریتم مبتنی بر ساختار داده «هرم دودویی» (Binary Heap) است. این الگوریتم مرتبسازی، مشابه با مرتبسازی انتخابی است که طی آن، عنصر بیشینه یافت میشود و در انتها قرار میگیرد. فرایند مشابهی برای دیگر عناصر باقیمانده نیز انجام میشود. در ادامه، این الگوریتم مرتب سازی آموزش داده شده و پیادهسازی آن در زبانهای برنامهنویسی گوناگون شامل «سیپلاسپلاس» (++C)، «سی» (C)، «جاوا» (Java)، «پایتون» (Python)، «سیشارپ» (#C) و «پیاچپی» (PHP) انجام شده است.
هرم دودویی چیست؟
ابتدا باید مفهوم «درخت دودویی کامل» (Complete Binary Tree) تعریف شود. یک درخت دودویی کامل، نوعی از درخت دودویی است که در هر سطح از آن، به جز احتمالا سطح آخر، به طور کامل پر شده است و همه گرهها تا حد امکان در چپ درخت قرار میگیرند. هرم دودویی یک درخت دودویی کامل است که در آن، عناصر به ترتیب خاصی قرار میگیرند که براساس آن گره والد بزرگتر (یا کوچکتر) از مقادیر موجود در دو گره فرزند خودش است. حالتی که والد از فرزند خود بزرگتر باشد را «هرم بیشینه» (Max Heap) و حالتی که والد از فرزند خود کوچکتر باشد را «هرم کمینه» (Min Heap) مینامند.
دلیل استفاده از نمایش آرایهای برای درخت دودویی
با توجه به اینکه هرم دودویی یک درخت دودویی کامل محسوب میشود، میتوان آن را به سادگی به عنوان یک آرایه نمایش داد. شایان توجه است که نمایش مبتنی بر آرایه، کارایی فضایی دارد. اگر گره والد در اندیس I ذخیره شده باشد، فرزند چپ را میتوان با و فرزند راست را با محاسبه کرد (با در نظر داشتن این فرض که اندیسها از صفر شروع میشوند).
الگوریتم مرتب سازی هرمی برای مرتبسازی صعودی
- هرم بیشینه را از دادههای ورودی بساز.
- در این نقطه، بزرگترین عنصر در ریشه هرم قرار دارد. آن را با آخرین عنصر هرم جایگزین و سایز هرم را یکی کاهش بده. در نهایت، ریشه درخت را هرمی کن.
- گامهای بالا را تا هنگامی که اندازه هرم بزرگتر از ۱ است ادامه بده.
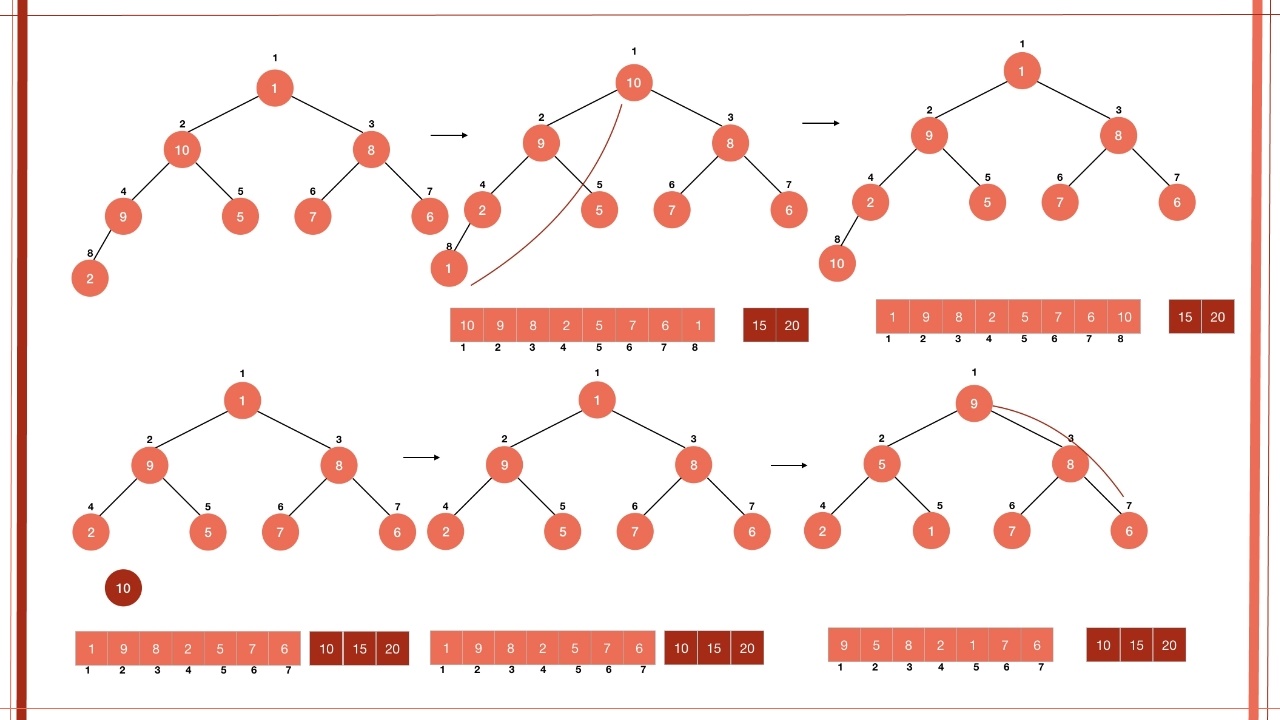
روش ساخت هرم
روال هرمیسازی را میتوان تنها هنگامی به یک گره اعمال کرد که گرههای فرزند آن هرمیسازی شده باشند. بنابراین، هرمیسازی باید به صورت «پایین به بالا» (Bottom Up) انجام شود. برای درک بهتر این مبحث، در ادامه یک مثال ارائه شده است.
Input data: 4, 10, 3, 5, 1
4(0)
/ \
10(1) 3(2)
/ \
5(3) 1(4)
.عدد موجود در پرانتز نشانگر اندیس در نمایش آرایهای دادهها است
:اعمال فرایند هرمیسازی به اندیس ۱
4(0)
/ \
10(1) 3(2)
/ \
5(3) 1(4)
:اعمال فرایند هرمیسازی به اندیس صفر
10(0)
/ \
5(1) 3(2)
/ \
4(3) 1(4)
.روال هرمیسازی خودش را به طور بازگشتی فراخوانی میکند تا یک هرم را به صورت بالا به پایین بسازد
مرتب سازی هرمی در C
مرتب سازی هرمی در ++C
مرتب سازی هرمی در جاوا
مرتب سازی هرمی در پایتون
مرتب سازی هرمی در #C
مرتب سازی هرمی در PHP
مرتبسازی هرمی یک الگوریتم «در جا» یا «در محل» (In-Place Algorithm) است. پیادهسازی متداول این الگوریتم «پایدار» (Stable) نیست، اما میتوان آن را پایدار کرد.
پیچیدگی زمانی هرمیسازی از درجه (O(Logn، پیچیدگی زمانی ()createAndBuildHeap از درجه (O(n و پیچیدگی زمانی کلی الگوریتم مرتبسازی هرمی از درجه (O(nLogn است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- آموزش ساختمان دادهها با C و ++C (همراه با حل نمونه سوالات کنکور ارشد)
- مجموعه آموزشهای برنامهنویسی
- مرتبسازی پشته با الگوریتم بازگشتی — به زبان ساده
- مرتبسازی درجی (Insertion Sort) — به زبان ساده
- مرتبسازی حبابی و پیاده سازی آن — از صفر تا صد
- مرتب سازی ادغامی چیست؟ – آموزش الگوریتم به زبان ساده
^^













ای کاش منبع مقاله هم ذکر میکردید چون کاملا ترجمه از لینک زیر هست
سلام، وقت شما بخیر؛
منابع تمامی مطالب در انتهای آنها ذکر شده است، از همراهی شما با مجله فرادرس بسیار سپاسگزاریم.
سلام خسته نباشید مطالب مفید بود من دنبال یه اپلیکیشن یا نرم افزاری میگردم ک بتونم اسامی رو به صورت درخت باینری به صورت هرمی در اورد من بازاریابی شبکه ای کار میکنم و لازمه ک تعداد نفرات رو توی یه برنامه جا بدم دیگ از درختی کشیدن دستی با خودکار روی کاغذ خسته شدم میشه کمکم کنید
مطالبتون خیلی مفیدن خانوم حصارکی شما بهترین نویسنده فرادرس هستید