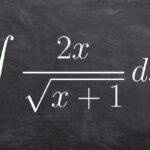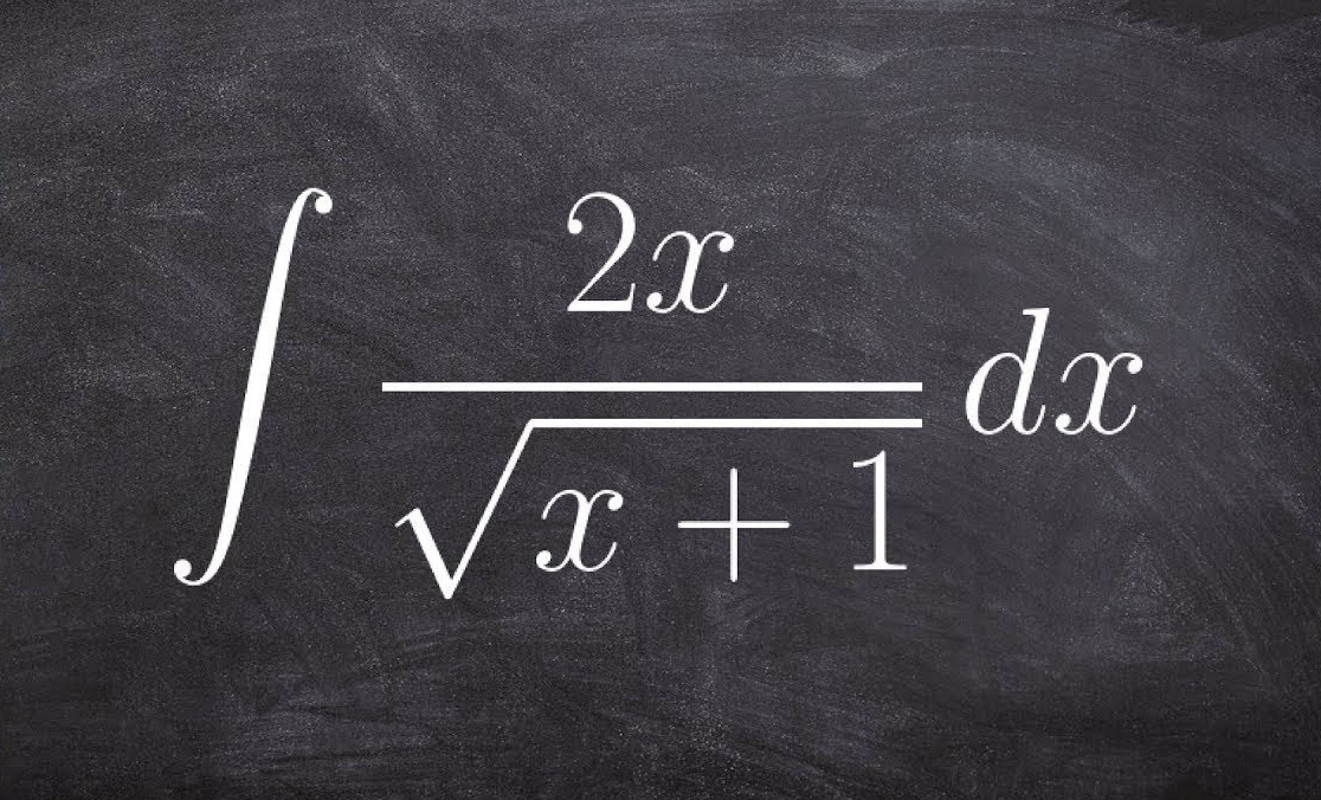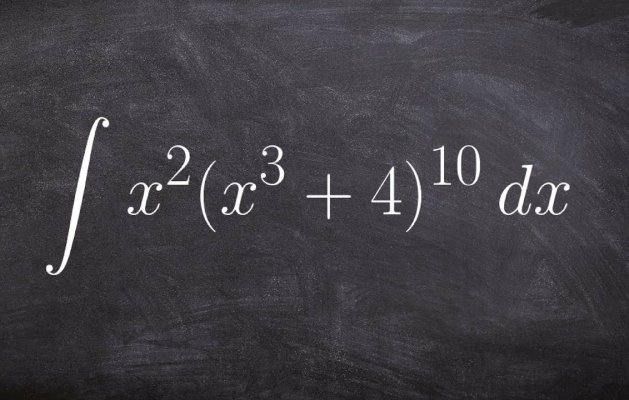در آموزشهای پیشین مجله فرادرس، با مفهوم انتگرال و روشهای انتگرالگیری آشنا شدیم. همچنین، مثالها و نمونهسؤالهای متنوعی از انتگرال را حل کردیم. در این آموزش، فهرستی از مهمترین فرمولها و قوانین انتگرال و انتگرالگیری را ارائه میکنیم. این کار را در دو بخش انجام خواهیم داد. در بخش اول، خلاصهای از مهمترین قوانین انتگرال را مرور میکنیم. در ادامه، یک فهرست مروری از فرمولهای کاربردی انتگرالگیری را بیان میکنیم.
مروری بر مفهوم انتگرال
تابع f ( x ) f (x ) f ( x ) I I I F ( x ) F(x) F ( x ) f ( x ) f (x ) f ( x ) x x x I I I
F ′ ( x ) = f ( x ) F^\prime\left( x \right) = f\left( x \right) F ′ ( x ) = f ( x )
تعریف انتگرال نامعین معادل این پادمشتق است. تعداد بینهایتی پادمشق برای تابع f ( x ) f ( x ) f ( x ) C C C
( F ( x ) + C ) ′ = F ′ ( x ) + C ′ = f ( x ) + 0 = f ( x ) \left( {F\left( x \right) + C} \right)^\prime = F^\prime\left( x \right) + C^\prime = f\left( x \right) + 0 = f\left( x \right) ( F ( x ) + C ) ′ = F ′ ( x ) + C ′ = f ( x ) + 0 = f ( x )
مجموعه همه پادمشتقهای تابع f ( x ) f (x ) f ( x ) f ( x ) f ( x ) f ( x )
∫ f ( x ) d x = F ( x ) + C , F ′ ( x ) = f ( x ) {\int} {{f\left( x \right)}{dx}} = F\left( x \right) + C,\;\;\text{}\;\;F^\prime\left( x \right) = f\left( x \right) ∫ f ( x ) d x = F ( x ) + C , F ′ ( x ) = f ( x )
در این تعریف، ∫ \int ∫ f ( x ) f (x ) f ( x ) x x x d x d x d x x x x C C C
قوانین انتگرال گیری
مهمترین ویژیگیها، فرمولها و قوانین انتگرال گیری، در جدول زیر بیان شدهاند.
∫ f ( x ) ± g ( x ) d x = ∫ f ( x ) d x ± ∫ g ( x ) d x \int f ( x ) \pm g ( x ) d x = \int f ( x ) d x \pm \int g ( x ) d x ∫ f ( x ) ± g ( x ) d x = ∫ f ( x ) d x ± ∫ g ( x ) d x ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x \int _ { a } ^ { b } c f ( x ) d x = c \int _ { a } ^ { b } f ( x ) d x ∫ a b c f ( x ) d x = c ∫ a b f ( x ) d x
∫ a b f ( x ) d x = − ∫ b a f ( x ) d x \int _ { a } ^ { b } f ( x ) d x = - \int _ { b } ^ { a } f ( x ) d x ∫ a b f ( x ) d x = − ∫ b a f ( x ) d x
∫ a b f ( x ) d x = F ( x ) ∣ a b = F ( b ) − F ( a ) F ( x ) = ∫ f ( x ) d x \begin {align} & \int _ { a } ^ { b} f ( x ) d x = \left . F ( x ) \right | _ { a } ^ { b } = F ( b ) - F ( a ) \\ & F ( x ) = \int f ( x ) d x \end {align} ∫ a b f ( x ) d x = F ( x ) ∣ a b = F ( b ) − F ( a ) F ( x ) = ∫ f ( x ) d x ∫ a a f ( x ) d x = 0 \int _ { a } ^ { a } f ( x ) d x = 0 ∫ a a f ( x ) d x = 0 ∫ a b c d x = c ( b − a ) \int _ { a } ^ { b } c d x = c ( b - a ) ∫ a b c d x = c ( b − a ) ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x \int _ { a } ^ { b } f ( x ) d x = \int _ { a } ^ { c } f ( x ) d x + \int _ { c } ^ { b } f ( x ) d x ∫ a b f ( x ) d x = ∫ a c f ( x ) d x + ∫ c b f ( x ) d x ∫ c f ( x ) d x = c ∫ f ( x ) d x \int c f ( x ) d x = c \int f ( x ) d x ∫ c f ( x ) d x = c ∫ f ( x ) d x
در ادامه، مهمترین فرمولهای انتگرالگیری را برای توابع مختلف بیان میکنیم.
قوانین انتگرال توابع چندجملهای و کسری
در جدول زیر، مهمترین فرمولها و قوانین انتگرال توابع چندجملهای و کسری را آوردهایم.
∫ k d x = k x + c \int k d x = k x + c ∫ k d x = k x + c ∫ d x = x + c \int d x = x + c ∫ d x = x + c ∫ 1 x d x = ln ∣ x ∣ + c \int \frac { 1 } { x } d x = \ln | x | + c ∫ x 1 d x = ln ∣ x ∣ + c ∫ x n d x = 1 n + 1 x n + 1 + c , n ≠ − 1 \int x ^ { n } d x = \frac { 1 } { n + 1 } x ^ {n + 1 } + c , n \neq - 1 ∫ x n d x = n + 1 1 x n + 1 + c , n = − 1 ∫ 1 a x + b d x = 1 a ln ∣ a x + b ∣ + c \int \frac { 1 } { a x + b } d x = \frac { 1 } { a } \ln | a x + b |+ c ∫ a x + b 1 d x = a 1 ln ∣ a x + b ∣ + c ∫ x − n d x = 1 1 − n x 1 − n + c , n ≠ 1 \int x ^ { - n } d x = \frac { 1 } { 1 - n } x ^ { 1 - n } + c , n \neq 1 ∫ x − n d x = 1 − n 1 x 1 − n + c , n = 1 ∫ ( a x + b ) d x = a 2 x 2 + b x + c \int ( a x + b ) d x = \frac { a } { 2 } x ^ { 2 } + b x + c ∫ ( a x + b ) d x = 2 a x 2 + b x + c ∫ x p q d x = 1 p q + 1 x ( p q + 1 ) + c = q q + p x p + q q + c \int x ^ { \frac { p } { q } } d x = \frac { 1 } { \frac { p }{ q } + 1 } x ^ { \left ( \frac { p } { q } + 1 \right ) } + c = \frac { q } { q + p } x ^ { \frac { p + q } { q } } + c ∫ x q p d x = q p + 1 1 x ( q p + 1 ) + c = q + p q x q p + q + c
برای آشنایی با این انتگرالها، به آموزشهای «انتگرال توابع کسری — از صفر تا صد (+ دانلود فیلم آموزش گام به گام) » و «انتگرال گیری به روش کسرهای جزئی — از صفر تا صد (+ دانلود فیلم آموزش رایگان) » مراجعه کنید.
قوانین انتگرال توابع مثلثاتی
مهمترین فرمولهای انتگرال توابع مثلثاتی را در جدول زیر آوردهایم.
∫ csc u cot u d u = − csc u + c \int \csc u \cot u d u = - \csc u + c ∫ csc u cot u d u = − csc u + c ∫ cos u d u = sin u + c \int \cos u d u = \sin u + c ∫ cos u d u = sin u + c ∫ csc 2 u d u = − cot u + c \int \csc ^ { 2 } u d u = -\cot u + c ∫ csc 2 u d u = − cot u + c ∫ sin u d u = − cos u + c \int \sin u d u = - \cos u + c ∫ sin u d u = − cos u + c ∫ tan u d u = ln ∣ sec u ∣ + c \int \tan u d u = \ln | \sec u | + c ∫ tan u d u = ln ∣ sec u ∣ + c ∫ sec 2 u d u = tan u + c \int \sec ^ { 2 } u d u = \tan u + c ∫ sec 2 u d u = tan u + c ∫ cot u d u = ln ∣ sin u ∣ + c \int \cot u d u = \ln | \sin u | + c ∫ cot u d u = ln ∣ sin u ∣ + c ∫ sec u tan u d u = sec u + c \int \sec u \tan u d u = \sec u + c ∫ sec u tan u d u = sec u + c ∫ sec 3 u d u = 1 2 ( sec u tan u + ln ∣ sec u + tan u ∣ ) + c \int \sec ^ { 3 } u d u = \frac { 1 } { 2 } ( \sec u \tan u + \ln | \sec u + \tan u | ) + c ∫ sec 3 u d u = 2 1 ( sec u tan u + ln ∣ sec u + tan u ∣ ) + c ∫ sec u d u = ln ∣ sec u + tan u ∣ + c \int \sec u d u = \ln |\sec u + \tan u | + c ∫ sec u d u = ln ∣ sec u + tan u ∣ + c ∫ csc 3 u d u = 1 2 ( − csc u cot u + ln ∣ csc u − cot u ∣ ) + c \int \csc ^ { 3 } u d u = \frac { 1 } { 2 } ( - \csc u \cot u + \ln | \csc u - \cot u | ) + c ∫ csc 3 u d u = 2 1 ( − csc u cot u + ln ∣ csc u − cot u ∣ ) + c ∫ csc u d u = ln ∣ csc u − cot u ∣ + c \int \csc u d u = \ln | \csc u - \cot u | + c ∫ csc u d u = ln ∣ csc u − cot u ∣ + c
قوانین انتگرال توابع لگاریتمی و نمایی
جدول زیر مهمترین فرمولهای انتگرال توابع لگاریتمی و نمایی را نشان میدهد.
∫ ln u d u = u ln u − u + c \int \ln u d u = u \ln u -u + c ∫ ln u d u = u ln u − u + c ∫ e u d u = e u + c \int e ^ { u } d u = e ^ { u } + c ∫ e u d u = e u + c ∫ u e u d u = ( u − 1 ) e u + c \int u e ^ { u } d u = ( u - 1 ) e ^ { u } + c ∫ u e u d u = ( u − 1 ) e u + c ∫ a u d u = a u ln a + c \int a ^ { u } d u = \frac { a ^ { u } } { \ln a } + c ∫ a u d u = ln a a u + c ∫ e a u sin ( b u ) = e a u a 2 + b 2 ( a sin ( b u ) − b cos ( b u ) ) + c \int e ^ { a u } \sin ( b u ) = \frac { e ^ { a u } } { a ^ { 2 } + b ^ { 2 } } ( a \sin ( b u ) - b \cos ( b u ) ) + c ∫ e a u sin ( b u ) = a 2 + b 2 e a u ( a sin ( b u ) − b cos ( b u )) + c ∫ 1 u ln u d u = ln ∣ ln u ∣ + c \int \frac { 1 } { u \ln u } d u = \ln | \ln u | + c ∫ u ln u 1 d u = ln ∣ ln u ∣ + c ∫ e a u cos ( b u ) = e a u a 2 + b 2 ( a cos ( b u ) + b sin ( b u ) ) + c \int e ^ { a u } \cos ( b u ) = \frac { e ^ { a u } } { a ^ { 2 } + b ^ { 2 } } ( a \cos ( b u ) + b \sin ( b u ) ) + c ∫ e a u cos ( b u ) = a 2 + b 2 e a u ( a cos ( b u ) + b sin ( b u )) + c ∫ u e c u d u = e c u ( c u − 1 ) c 2 + c \int u e ^ { c u } d u = \frac { e ^ { c u } ( c u - 1 ) }{ c ^ { 2 } } + c ∫ u e c u d u = c 2 e c u ( c u − 1 ) + c
برای آشنایی بیشتر با این انتگرالها، به آموزشهای «انتگرال توابع نمایی – از صفر تا صد » و «انتگرال lnx — به زبان ساده (+ دانلود فیلم آموزش گام به گام) » مراجعه کنید.
قوانین انتگرال توابع معکوس مثلثاتی
جدول زیر، مهمترین قوانین انتگرال توابع معکوس مثلثاتی را نشان میدهد.
∫ tan − 1 u d u = u tan − 1 u − 1 2 ln ( 1 + u 2 ) + c \int \tan ^ { - 1 } u d u = u \tan ^ { - 1 } u - \frac { 1 } { 2 } \ln \left ( 1 + u ^ { 2 } \right ) + c ∫ tan − 1 u d u = u tan − 1 u − 2 1 ln ( 1 + u 2 ) + c ∫ 1 a 2 − u 2 d u = sin − 1 u a + c \int \frac { 1 } { \sqrt { a ^ { 2 } - u ^ { 2 } } } d u = \sin ^ { - 1 } \frac { u } { a } + c ∫ a 2 − u 2 1 d u = sin − 1 a u + c ∫ cos − 1 u d u = u cos − 1 u − 1 − u 2 + c \int \cos ^ { - 1 } u d u = u \cos ^ { - 1 } u - \sqrt { 1 - u ^ { 2 } } + c ∫ cos − 1 u d u = u cos − 1 u − 1 − u 2 + c ∫ 1 a 2 + u 2 d u = 1 a tan − 1 ( u a ) + c \int \frac { 1 } { a ^ { 2 } + u ^ { 2 } } d u = \frac { 1 } { a } \tan ^ { - 1 } \left ( \frac { u } { a } \right ) + c ∫ a 2 + u 2 1 d u = a 1 tan − 1 ( a u ) + c ∫ sin − 1 u d u = u sin − 1 u + 1 − u 2 + c \int \sin ^ { - 1 } u d u = u \sin ^ { - 1 } u + \sqrt { 1 -u ^ { 2 } } + c ∫ sin − 1 u d u = u sin − 1 u + 1 − u 2 + c ∫ 1 u u 2 − a 2 d u = 1 a sec − 1 ( u a ) + c \int \frac { 1 } { u \sqrt { u ^ { 2 } - a ^ { 2 } } } d u = \frac { 1 } { a } \sec ^ { - 1 } \left ( \frac { u } { a } \right ) + c ∫ u u 2 − a 2 1 d u = a 1 sec − 1 ( a u ) + c
قوانین انتگرال توابع هیپربولیکی
مهمترین قوانین انتگرال توابع هیپربولیکی در جدول زیر آورده شده است.
∫ sech u tanh u d u = − sech u + c \int \operatorname {sech} u \tanh u d u = - \operatorname {sech} u + c ∫ sech u tanh u d u = − sech u + c ∫ sinh u d u = cosh u + c \int \sinh u d u = \cosh u + c ∫ sinh u d u = cosh u + c ∫ csch u coth u d u = − csch u + c \int \operatorname {csch} u \operatorname {coth} u d u = - \operatorname {csch} u + c ∫ csch u coth u d u = − csch u + c ∫ cosh u d u = sinh u + c \int \cosh u d u = \sinh u + c ∫ cosh u d u = sinh u + c ∫ sech u d u = tan − 1 ∣ sinh u ∣ + c \int \operatorname {sech} u d u = \tan ^ { - 1 } | \sinh u | + c ∫ sech u d u = tan − 1 ∣ sinh u ∣ + c ∫ tanh u d u = ln cosh u + c \int \tanh u d u = \ln \cosh u + c ∫ tanh u d u = ln cosh u + c ∫ csch 2 u d u = − coth u + c \int \operatorname {csch} ^ { 2 } u d u = - \operatorname {coth} u + c ∫ csch 2 u d u = − coth u + c ∫ sech 2 u d u = tanh u + c \int \operatorname {sech} ^ { 2 } u d u = \tanh u + c ∫ sech 2 u d u = tanh u + c
برای آشنایی بیشتر با انتگرال این توابع، به آموزش «انتگرال توابع هیپربولیک — از صفر تا صد (+ دانلود فیلم آموزش گام به گام) » مراجعه کنید.
انتگرال چند تابع پرکاربرد
در جدول زیر، فرمولهای چند انتگرال مهم و پرکاربرد را آوردهایم.
∫ 1 u 2 − a 2 d u = 1 2 a ln ∣ u − a u + a ∣ + c \int \frac { 1 } { u ^ { 2 } - a ^ { 2 } } d u = \frac { 1 } { 2 a } \ln \left | \frac { u - a } { u + a } \right | + c ∫ u 2 − a 2 1 d u = 2 a 1 ln u + a u − a + c ∫ 1 a 2 − u 2 d u = 1 2 a ln ∣ u + a u − a ∣ + c \int \frac { 1 } { a ^ { 2 } - u ^ { 2 } } d u = \frac { 1 } { 2 a } \ln \left | \frac { u + a } { u - a } \right | + c ∫ a 2 − u 2 1 d u = 2 a 1 ln u − a u + a + c ∫ u 2 − a 2 d u = u 2 u 2 − a 2 − a 2 2 ln ∣ u + u 2 − a 2 ∣ + c \int \sqrt { u ^ { 2 } - a ^ { 2 } } d u = \frac { u } { 2 } \sqrt { u ^ { 2 } - a ^ { 2 } } - \frac { a ^ { 2 } } { 2 } \ln \left | u + \sqrt { u ^ { 2 } - a ^ { 2 } } \right | + c ∫ u 2 − a 2 d u = 2 u u 2 − a 2 − 2 a 2 ln u + u 2 − a 2 + c ∫ a 2 + u 2 d u = u 2 a 2 + u 2 + a 2 2 ln ∣ u + a 2 + u 2 ∣ + c \int \sqrt { a ^ { 2 } + u ^ { 2 } } d u = \frac { u } { 2 } \sqrt { a ^ { 2 } + u ^ { 2 } } + \frac { a ^ { 2 } } { 2 } \ln \left | u + \sqrt { a ^ { 2 } + u ^ { 2 } } \right | + c ∫ a 2 + u 2 d u = 2 u a 2 + u 2 + 2 a 2 ln u + a 2 + u 2 + c ∫ 2 a u − u 2 d u = u − a 2 2 a u − u 2 + a 2 2 cos − 1 a − u a + c \int \sqrt { 2 a u - u ^ { 2 } } d u = \frac { u - a } { 2 } \sqrt { 2 a u - u ^ { 2 } } + \frac { a ^ { 2 } } { 2 } \cos ^ { - 1 } \frac { a - u } { a } + c ∫ 2 a u − u 2 d u = 2 u − a 2 a u − u 2 + 2 a 2 cos − 1 a a − u + c ∫ a 2 − u 2 d u = u 2 a 2 − u 2 + a 2 2 sin − 1 u a + c \int \sqrt { a ^ { 2 } - u ^ { 2 } } d u = \frac { u } { 2 } \sqrt { a ^ { 2 } - u ^ { 2 } } + \frac { a ^ { 2 } } { 2 } \sin ^ { - 1 } \frac { u } { a } + c ∫ a 2 − u 2 d u = 2 u a 2 − u 2 + 2 a 2 sin − 1 a u + c
PDF رایگان قوانین انتگرال گیری
قوانین انتگرال گیری از جمله مواردی هستند که ممکن است در موقعیتهای مختلف مورد نیاز دانشآموزان، دانشجویان و کسانی باشد که به هر دلیلی به آنها نیاز دارند. برای دسترسی یکجا به فرمولهایی که بیان کردیم، فایل پی دی اف قوانین انتگرال را در قالب یک تقلبنامه آماده کردهایم که در ادامه میتوانید آن را دانلود کنید. فهرست مطالب این تقلبنامه در ادامه آورده شده است.
ویژگیها و قوانین حاکم در انتگرالگیری
انتگرال توابع چند جملهای و کسری
انتگرال توابع مثلثاتی
انتگرال توابع معکوس مثلثاتی
انتگرال توابع لگاریتمی و نمایی
انتگرال توابع هایپربولیکی
روشهای انتگرالگیری
کاربردهای انتگرال
مفاهیم انتگرال سره و ناسره
محاسبه عددی انتگرال
این تقلبنامه را میتوانید با کلیک روی لینک زیر دانلود کنید.
دانلود تقلبنامه (+ کلیک کنید)
مثالهای کاربرد قوانین انتگرال
در این بخش، چند مثال را از کاربرد فرمولهایی که بیان کردیم، بررسی میکنیم.
مثال اول قوانین انتگرال
انتگرال زیر را حل کنید.
∫ ( 3 x 2 − 6 x + 2 cos x ) d x \int { \left ( { 3 { x ^ 2 } - 6 x + 2 \cos x } \right ) d x } ∫ ( 3 x 2 − 6 x + 2 cos x ) d x
جواب: با توجه به فرمولها و قوانینی که دیدیم، خواهیم داشت:
I = ∫ ( 3 x 2 − 6 x + 2 cos x ) d x = ∫ 3 x 2 d x − ∫ 6 x d x + ∫ 2 cos x d x = 3 ∫ x 2 d x − 6 ∫ x d x + 2 ∫ cos x d x \begin {align} I & = \int { \left ( { 3 { x ^ 2 } - 6 x + 2 \cos x } \right ) d x } \\ & = \int { 3 { x ^ 2 } d x } - \int { 6 x d x } + \int { 2 \cos x d x } \\ & = 3 { \int { { x ^ 2 } d x } } - 6 { \int { x d x } } + 2 { \int { \cos x d x } } \end {align} I = ∫ ( 3 x 2 − 6 x + 2 cos x ) d x = ∫ 3 x 2 d x − ∫ 6 x d x + ∫ 2 cos x d x = 3 ∫ x 2 d x − 6 ∫ x d x + 2 ∫ cos x d x
سه انتگرال را میتوان با استفاده از فرمولهایی که در ابتدای آموزش ارائه کردیم، حل کرد:
I = 3 ⋅ x 3 3 − 6 ⋅ x 2 2 + 2 ⋅ sin x + C = x 3 − 3 x 2 + 2 sin x + C I = 3 \cdot { \frac { { { x ^ 3 } } } { 3 } } - 6 \cdot { \frac { { { x ^ 2 } } } { 2 } } + 2 \cdot { \sin x } + C = { x ^ 3 } - 3 { x ^ 2 } + 2 \sin x + C I = 3 ⋅ 3 x 3 − 6 ⋅ 2 x 2 + 2 ⋅ sin x + C = x 3 − 3 x 2 + 2 sin x + C
مثال دوم قوانین انتگرال
انتگرال ∫ ( 1 + x ) ( 1 + 2 x ) d x \int { \left ( { 1 + x } \right ) \left ( { 1 + 2 x } \right ) d x } ∫ ( 1 + x ) ( 1 + 2 x ) d x
جواب: انتگرالده را میتوان بهصورت زیر ساده کرد:
( 1 + x ) ( 1 + 2 x ) = 1 + x + 2 x + 2 x 2 = 2 x 2 + 3 x + 1 \left ( { 1 + x } \right ) \left ( { 1 + 2 x } \right ) = 1 + x + 2 x + 2 { x ^ 2 } = 2 { x ^ 2 } + 3 x + 1 ( 1 + x ) ( 1 + 2 x ) = 1 + x + 2 x + 2 x 2 = 2 x 2 + 3 x + 1
و انتگرال بهصورت زیر حل میشود:
∫ ( 1 + x ) ( 1 + 2 x ) d x = ∫ ( 2 x 2 + 3 x + 1 ) d x = ∫ 2 x 2 d x + ∫ 3 x d x + ∫ 1 d x = 2 ∫ x 2 d x + 3 ∫ x d x + ∫ d x = 2 ⋅ x 3 3 + 3 ⋅ x 2 2 + x + C = 2 x 3 3 + 3 x 2 2 + x + C \begin {align} \int { \left ( { 1 + x } \right ) \left ( { 1 + 2 x } \right ) d x } & = \int { \left ( { 2 { x ^ 2 } + 3 x + 1 } \right ) d x } = \int { 2 { x ^ 2 } d x } + \int { 3 x d x } + \int { 1 d x } \\ & = 2 \int { { x ^ 2 } d x } + 3 \int { x d x } + \int { d x } = 2 \cdot \frac { { { x ^ 3 } } } { 3 } + 3 \cdot \frac { { { x ^ 2 } } } { 2 } + x + C \\ & = \frac { { 2 { x ^ 3 } } } { 3 } + \frac { { 3 { x ^ 2 } } } { 2 } + x + C \end {align} ∫ ( 1 + x ) ( 1 + 2 x ) d x = ∫ ( 2 x 2 + 3 x + 1 ) d x = ∫ 2 x 2 d x + ∫ 3 x d x + ∫ 1 d x = 2 ∫ x 2 d x + 3 ∫ x d x + ∫ d x = 2 ⋅ 3 x 3 + 3 ⋅ 2 x 2 + x + C = 3 2 x 3 + 2 3 x 2 + x + C
مثال سوم قوانین انتگرال
انتگرال زیر را حل کنید.
∫ ( 1 x 2 − 1 x 3 ) d x \int { \left ( { \frac { 1 } { { { x ^ 2 } } } - \frac { 1 }{ { { x ^ 3 } } } } \right ) d x } ∫ ( x 2 1 − x 3 1 ) d x
جواب: طبق قانون جمع، داریم:
I = ∫ ( 1 x 2 − 1 x 3 ) d x = ∫ d x x 2 − ∫ d x x 3 I = \int { \left ( { \frac { 1 } { { { x ^ 2 } } } - \frac { 1 }{ { { x ^ 3 } } } } \right ) d x } = \int { \frac { { d x } } { { { x ^ 2 } } } } - \int { \frac { { d x } } { {{ x ^ 3 } }} } I = ∫ ( x 2 1 − x 3 1 ) d x = ∫ x 2 d x − ∫ x 3 d x
هر دو انتگرالده توابع توانی هستند و بنابراین، خواهیم داشت:
I = ∫ x − 2 d x − ∫ x − 3 d x = x − 1 ( − 1 ) − x − 2 ( − 2 ) + C = − 1 x + 1 2 x 2 + C I = \int { { x ^ { - 2 } } dx } - \int { { x ^ { - 3 } } d x } = \frac { { { x ^ { - 1 } } } } { { \left ( { - 1 } \right ) } } - \frac { { { x ^ { - 2 } } } } { { \left ( { - 2 } \right ) } } + C = - \frac { 1 } { x } + \frac { 1 } { { 2 { x ^ 2 } } } + C I = ∫ x − 2 d x − ∫ x − 3 d x = ( − 1 ) x − 1 − ( − 2 ) x − 2 + C = − x 1 + 2 x 2 1 + C
مثال چهارم قوانین انتگرال
انتگرال زیر را محاسبه کنید.
∫ ( x + x 3 ) d x \int { \left ( { \sqrt x + \sqrt[3] { x } } \right ) d x } ∫ ( x + 3 x ) d x
جواب: حاصل انتگرال بهصورت زیر خواهد بود:
∫ ( x + x 3 ) d x = ∫ x d x + ∫ x 3 d x = ∫ x 1 2 d x + ∫ x 1 3 d x = x 1 2 + 1 1 2 + 1 + x 1 3 + 1 1 3 + 1 + C = 2 x 3 2 3 + 3 x 4 3 4 = 2 x 3 3 + 3 x 4 3 4 + C \begin {align} \int { \left ( { \sqrt x + \sqrt[3] { x } } \right ) d x }& = \int { \sqrt x d x } + \int { \sqrt[3] { x } d x } = \int { { x ^ { \frac { 1 } { 2 } } } d x } + \int { { x ^ { \frac { 1 }{ 3 } } } d x } \\ &= \frac { { { x ^ { \frac { 1 } { 2 } + 1 } } } } { { \frac { 1 } { 2 } + 1 } } + \frac { { { x ^ { \frac { 1 } { 3 } + 1 } } } } { { \frac { 1 } { 3 } + 1 } } + C = \frac { { 2 { x ^ { \frac { 3 } { 2 } }} } } { 3 } + \frac { { 3 { x ^ { \frac { 4 } { 3 } } } } } { 4 } \\ & = \frac { { 2 \sqrt { { x ^ 3 } } } } { 3 } + \frac { { 3 \sqrt [3] { { { x ^ 4 } } } } } { 4 } + C \end {align} ∫ ( x + 3 x ) d x = ∫ x d x + ∫ 3 x d x = ∫ x 2 1 d x + ∫ x 3 1 d x = 2 1 + 1 x 2 1 + 1 + 3 1 + 1 x 3 1 + 1 + C = 3 2 x 2 3 + 4 3 x 3 4 = 3 2 x 3 + 4 3 3 x 4 + C
مثال پنجم قوانین انتگرال
جواب انتگرال زیر را محاسبه کنید.
∫ x + 1 x d x \int { \frac { { x + 1 } } { { \sqrt x } } d x } ∫ x x + 1 d x
جواب: حاصل انتگرال بهصورت زیر است:
∫ x + 1 x d x = ∫ ( x x + 1 x ) d x = ∫ ( x + 1 x ) d x = ∫ x d x + ∫ d x x = x 3 2 3 2 + 2 x + C = 2 x 3 3 + 2 x + C \begin {align} \int { \frac { { x + 1 } } { { \sqrt x } } d x } & = \int {\left ( { \frac { x } { { \sqrt x } } + \frac { 1 } { { \sqrt x } } } \right ) d x } = \int { \left ( { \sqrt x + \frac { 1 } { { \sqrt x } } } \right ) d x } \\ & = \int { \sqrt x d x } + \int { \frac { { d x } } { { \sqrt x } } } = \frac { { { x ^ { \frac { 3 } { 2 } } } } } { { \frac { 3 } { 2 } } } + 2 \sqrt x + C \\ & = \frac { { 2 \sqrt { { x ^ 3 } } } } { 3 } + 2 \sqrt x + C \end {align} ∫ x x + 1 d x = ∫ ( x x + x 1 ) d x = ∫ ( x + x 1 ) d x = ∫ x d x + ∫ x d x = 2 3 x 2 3 + 2 x + C = 3 2 x 3 + 2 x + C
مثال ششم قوانین انتگرال
حاصل انتگرال زیر را محاسبه کنید.
∫ ( x 3 + e 3 ) d x \int { \left ( { \sqrt [3] { x } + { e ^ 3 } } \right ) d x } ∫ ( 3 x + e 3 ) d x
جواب: این انتگرال را بهصورت زیر مینویسیم:
I = ∫ ( x 3 + e 3 ) d x = ∫ ( x 1 3 + e 3 ) d x = ∫ x 1 3 d x + ∫ e 3 d x = ∫ x 1 3 d x + e 3 ∫ d x \begin {align} I & = \int { \left ( { \sqrt [3] { x } + { e ^ 3 } } \right ) d x } = \int { \left ( { { x ^ { \frac { 1 } { 3 } } } + { e ^ 3 } } \right ) d x } \\ & = \int { { x ^ { \frac { 1 } { 3 } } } d x } + \int { { e ^ 3 } d x } = \int { { x ^ { \frac { 1 } { 3 } } } d x } + { e ^ 3 } \int { d x } \end {align} I = ∫ ( 3 x + e 3 ) d x = ∫ ( x 3 1 + e 3 ) d x = ∫ x 3 1 d x + ∫ e 3 d x = ∫ x 3 1 d x + e 3 ∫ d x
با کمک جدول انتگرالها، خواهیم داشت:
I = ∫ x 1 3 d x + e 3 ∫ d x = x 4 3 4 3 + e 3 x + C = 3 x 4 3 4 + e 3 x + C I = \int { { x ^ { \frac { 1 } { 3 } } } d x } + { e ^ 3 } \int { d x } = \frac { { { x ^ { \frac { 4 } { 3 } } } } } { { \frac { 4 } { 3 } } } + { e ^ 3 } x + C = \frac { { 3 \sqrt [3] { { { x ^ 4 } } } } } { 4 } + { e ^ 3 } x + C I = ∫ x 3 1 d x + e 3 ∫ d x = 3 4 x 3 4 + e 3 x + C = 4 3 3 x 4 + e 3 x + C
مثال هفتم قوانین انتگرال
انتگرال زیر را محاسبه کنید.
∫ 4 d x 2 + 3 x 2 \int { \frac { { 4 d x } } { { 2 + 3 { x ^ 2 } } } } ∫ 2 + 3 x 2 4 d x
جواب: از جدول انتگرال استفاده میکنیم و مینویسیم:
∫ d x a 2 + x 2 = 1 a arctan x a + C \int { \frac { { d x } } { { { a ^ 2 } + { x ^ 2 } } } = \frac { 1 } { a } } \arctan { \frac { x } { a } } + C ∫ a 2 + x 2 d x = a 1 arctan a x + C
بنابراین، جواب بهصورت زیر خواهد بود:
∫ 4 d x 2 + 3 x 2 = 4 ∫ d x 3 ( 2 3 + x 2 ) = 4 3 ∫ d x ( 2 3 ) 2 + x 2 = 4 3 ⋅ 1 2 3 arctan x 2 3 + C = 4 6 arctan 3 x 2 + C \begin {align} \int { \frac { { 4 d x } } { { 2 + 3 { x ^ 2 } } } } & = 4 \int { \frac { { d x } } { { 3 \left ( { \frac { 2 } { 3 } + { x ^ 2 } } \right ) } } } = \frac { 4 } { 3 } \int { \frac { { d x } } { { { { \left ( { \sqrt { \frac { 2 }{ 3 } } } \right ) } ^ 2 } + { x ^ 2 } } } } \\ & = \frac { 4 } { 3 } \cdot \frac { 1 } { { \sqrt { \frac { 2 } { 3 } } } } \arctan \frac { x } { { \sqrt { \frac { 2 }{ 3 } } } } + C = \frac { 4 } { { \sqrt 6 } } \arctan \frac { { \sqrt 3 x } } { { \sqrt 2 } } + C \end {align} ∫ 2 + 3 x 2 4 d x = 4 ∫ 3 ( 3 2 + x 2 ) d x = 3 4 ∫ ( 3 2 ) 2 + x 2 d x = 3 4 ⋅ 3 2 1 arctan 3 2 x + C = 6 4 arctan 2 3 x + C
مثال هشتم قوانین انتگرال
حاصل انتگرال ∫ x 2 1 + x 2 d x \int { \frac { { { x ^ 2 } } } { { 1 + { x ^ 2 } } } d x } ∫ 1 + x 2 x 2 d x
جواب: این انتگرال را بهصورت زیر مینویسیم:
I = ∫ d x 1 + 2 x 2 = ∫ d x 2 ( 1 2 + x 2 ) = 1 2 ∫ d x 1 2 + x 2 = 1 2 ∫ d x ( 1 2 ) 2 + x 2 I = \int { \frac { { d x} } { { 1 + 2 { x ^ 2 } } } } = \int { \frac { { d x } } { { 2 \left ( { \frac { 1 } { 2 } + { x ^ 2 } } \right ) } } } = \frac { 1 } { 2 } \int { \frac { { d x } } { { \frac { 1 } { 2 } + { x ^ 2 } } }} = \frac { 1 } { 2 } \int { \frac { { d x } } { { { { \left ( { \frac { 1 } { { \sqrt 2 } } } \right ) } ^ 2 } + { x ^ 2 } } } } I = ∫ 1 + 2 x 2 d x = ∫ 2 ( 2 1 + x 2 ) d x = 2 1 ∫ 2 1 + x 2 d x = 2 1 ∫ ( 2 1 ) 2 + x 2 d x
با توجه به جدول انتگرالها، داریم:
∫ d x a 2 + x 2 = 1 a arctan x a \int { \frac { { d x } } { { { a ^ 2 } + { x ^ 2 } } } } = { \frac { 1 } { a } } \arctan { \frac { x } { a } } ∫ a 2 + x 2 d x = a 1 arctan a x
بنابراین، خواهیم داشت:
I = 1 2 ∫ d x ( 1 2 ) 2 + x 2 = 1 2 ⋅ 1 1 2 arctan x 1 2 + C = 2 2 arctan ( 2 x ) + C = 1 2 arctan ( 2 x ) + C \begin {align} I & = \frac { 1 } { 2 } \int { \frac { { d x } }{ { { { \left ( { \frac { 1 } { { \sqrt 2 } } } \right ) } ^ 2 } + { x ^ 2 } } } } = \frac { 1 } { 2 } \cdot \frac { 1 } { { \frac { 1 } { { \sqrt 2 } } } } \arctan \frac { x } { { \frac { 1 } { { \sqrt 2 } } } } + C \\ & = \frac { { \sqrt 2 } } { 2 } \arctan \left ( { \sqrt 2 x } \right ) + C = \frac { 1 } { { \sqrt 2 } } \arctan \left ( { \sqrt 2 x } \right ) + C \end {align} I = 2 1 ∫ ( 2 1 ) 2 + x 2 d x = 2 1 ⋅ 2 1 1 arctan 2 1 x + C = 2 2 arctan ( 2 x ) + C = 2 1 arctan ( 2 x ) + C
مثال نهم قوانین انتگرال
جواب انتگرال زیر را محاسبه کنید:
∫ π d x π − x 2 \int { \frac { { \pi d x } } { { \sqrt { \pi - { x ^ 2 } } } } } ∫ π − x 2 π d x
جواب: از فرمول زیر استفاده میکنیم:
∫ d x a 2 − x 2 = arcsin x a + C \int { \frac { { d x } } { { \sqrt { { a ^ 2 } - { x ^ 2 } } } } } = \arcsin { \frac { x } { a } } + C ∫ a 2 − x 2 d x = arcsin a x + C
و خواهیم داشت:
∫ π d x π − x 2 = π ∫ d x ( π ) 2 − x 2 = π arcsin x π + C \int { \frac { { \pi d x} } { { \sqrt { \pi - { x ^ 2 } } } } } = \pi \int { \frac { { d x } } { { \sqrt { { { \left ( { \sqrt \pi } \right ) } ^ 2 } - { x ^ 2 } } } } } = \pi \arcsin \frac { x } { { \sqrt \pi } } + C ∫ π − x 2 π d x = π ∫ ( π ) 2 − x 2 d x = π arcsin π x + C
مثال دهم قوانین انتگرال
حاصل انتگرال زیر را محاسبه کنید:
∫ ( 2 cos x − 5 sin x ) d x \int { \left ( { 2 \cos x - 5 \sin x } \right ) d x } ∫ ( 2 cos x − 5 sin x ) d x
جواب: این انتگرال، بهراحتی، بهصورت زیر قابل محاسبه است:
∫ ( 2 cos x − 5 sin x ) d x = ∫ 2 cos x d x − ∫ 5 sin x d x = 2 ∫ cos x d x − 5 ∫ sin x d x = 2 ⋅ sin x − 5 ⋅ ( − cos x ) + C = 2 sin x + 5 cos x + C \begin {align} \int { \left ( { 2 \cos x - 5 \sin x } \right ) d x } & = \int { 2 \cos x d x } - \int { 5 \sin x d x } = 2 \int { \cos x d x } - 5 \int { \sin x d x } \\ & = 2 \cdot \sin x - 5 \cdot \left ( { - \cos x } \right ) + C = 2 \sin x + 5 \cos x + C \end {align} ∫ ( 2 cos x − 5 sin x ) d x = ∫ 2 cos x d x − ∫ 5 sin x d x = 2 ∫ cos x d x − 5 ∫ sin x d x = 2 ⋅ sin x − 5 ⋅ ( − cos x ) + C = 2 sin x + 5 cos x + C
مثال یازدهم قوانین انتگرال
حاصل انتگرال زیر را بهدست آورید:
∫ d x 1 − x 2 2 \int { \frac { { d x } } { { \sqrt { 1 - \frac { { { x ^ 2 } } } { 2 } } } } } ∫ 1 − 2 x 2 d x
جواب: انتگرال را میتوان بهصورت زیر بازنویسی کرد:
I = ∫ d x 1 − x 2 2 = ∫ d x 1 2 ( 2 − x 2 ) = ∫ d x 1 2 2 − x 2 = 2 ∫ d x 2 − x 2 = 2 ∫ d x ( 2 ) 2 − x 2 \begin {align} I & = \int { \frac { { d x } } { { \sqrt { 1 - \frac { { { x ^ 2 } } } { 2 } } } } } = \int { \frac { { d x } }{ { \sqrt { \frac { 1 } { 2 } \left ( { 2 - { x ^ 2 } } \right ) } } } } = \int { \frac { { d x } } { { \sqrt { \frac { 1 } { 2 } } \sqrt { 2 - { x ^ 2 } } } } } \\ & = \sqrt 2 \int { \frac { { d x } } { { \sqrt { 2 - { x ^ 2 } } } } } = \sqrt 2 \int { \frac { { d x } } { { \sqrt { { { \left ( { \sqrt 2 } \right ) } ^ 2 } - { x ^ 2 } } } } } \end {align} I = ∫ 1 − 2 x 2 d x = ∫ 2 1 ( 2 − x 2 ) d x = ∫ 2 1 2 − x 2 d x = 2 ∫ 2 − x 2 d x = 2 ∫ ( 2 ) 2 − x 2 d x
از فرمول زیر استفاده میکنیم:
∫ d x a 2 − x 2 = arcsin x a \int { \frac { { d x } } { { \sqrt { { a ^ 2 } - { x ^ 2 } } } } } = \arcsin { \frac { x } { a } } ∫ a 2 − x 2 d x = arcsin a x
و خواهیم داشت:
I = 2 ∫ d x ( 2 ) 2 − x 2 = 2 arcsin x 2 + C I = \sqrt 2 \int { \frac { { d x } } { { \sqrt { { { \left ( { \sqrt 2 } \right ) } ^ 2 } - { x ^ 2 } } } } } = \sqrt 2 \arcsin \frac { x } { { \sqrt 2 } } + C I = 2 ∫ ( 2 ) 2 − x 2 d x = 2 arcsin 2 x + C
مثال دوازدهم قوانین انتگرال
حاصل ∫ tan 2 x d x \int { { { \tan } ^ 2 } x d x } ∫ tan 2 x d x
جواب: از تساوی زیر استفاده میکنیم:
tan 2 x = sec 2 x − 1 { \tan ^ 2 } x = { \sec ^ 2 } x - 1 tan 2 x = sec 2 x − 1
و انتگرال را محاسبه میکنیم:
∫ tan 2 x d x = ∫ ( sec 2 x − 1 ) d x = ∫ sec 2 x d x − ∫ d x = tan x − x + C \int { { { \tan } ^ 2 } x d x } = \int { \left ( { { { \sec } ^ 2 } x - 1 } \right ) d x } = \int { { { \sec } ^ 2 } x d x } - \int { d x } = \tan x - x + C ∫ tan 2 x d x = ∫ ( sec 2 x − 1 ) d x = ∫ sec 2 x d x − ∫ d x = tan x − x + C
مثال سیزدهم قوانین انتگرال
انتگرال ∫ cot 2 x d x \int {{{\cot }^2}xdx} ∫ cot 2 x d x
جواب: از اتحاد زیر استفاده میکنیم:
1 sin 2 x − cot 2 x = 1 , ⇒ cot 2 x = 1 sin 2 x − 1 \frac { 1 } { { { { \sin } ^ 2 } x } } - { \cot ^ 2 } x = 1 , \; \; \Rightarrow { \cot ^ 2 } x = \frac { 1 } { { { { \sin } ^ 2 } x } } - 1 sin 2 x 1 − cot 2 x = 1 , ⇒ cot 2 x = sin 2 x 1 − 1
سپس، انتگرال را بهصورت مجموع دو انتگرال مینویسیم:
I = ∫ cot 2 x d x = ∫ ( 1 sin 2 x − 1 ) d x = ∫ d x sin 2 x − ∫ d x I = \int { { { \cot } ^ 2 } x d x } = \int { \left ( { \frac { 1 } { { { { \sin } ^ 2 } x } } - 1 } \right ) d x } = \int { \frac { { d x } } { { { { \sin } ^ 2 } x } } } - \int { d x } I = ∫ cot 2 x d x = ∫ ( sin 2 x 1 − 1 ) d x = ∫ sin 2 x d x − ∫ d x
در نتیجه، خواهیم داشت:
I = ∫ d x sin 2 x − ∫ d x = − cot x − x + C I = \int { \frac { { d x } } { { { { \sin } ^ 2 } x } } } - \int { d x } = - \cot x - x + C I = ∫ sin 2 x d x − ∫ d x = − cot x − x + C
مثال چهاردهم قوانین انتگرال
انتگرال زیر را محاسبه کنید.
∫ d x sin 2 2 x \int { \frac { { d x } } { { { \sin ^ 2 } 2 x } } } ∫ sin 2 2 x d x
جواب: از فرمولهای زیر استفاده میکنیم:
sin 2 x = 2 sin x cos x \sin 2 x = 2 \sin x \cos x sin 2 x = 2 sin x cos x
و
sin 2 x + cos 2 x = 1 { \sin ^ 2 } x + { \cos ^ 2 } x = 1 sin 2 x + cos 2 x = 1
بنابراین، خواهیم داشت:
∫ d x sin 2 2 x = 1 4 ∫ d x sin 2 x cos 2 x = 1 4 ∫ ( sin 2 x + cos 2 x ) d x sin 2 x cos 2 x = 1 4 ∫ ( 1 cos 2 x + 1 sin 2 x ) d x = 1 4 ∫ sec 2 x d x + 1 4 ∫ csc 2 x d x = 1 4 tan x − 1 4 cot x + C = 1 4 ( tan x − cot x ) + C \begin {align} \int { \frac { { d x } } { { { \sin ^ 2 } 2 x } } } & = \frac { 1 } { 4 } \int { \frac { { d x } } { { { \sin ^ 2 } x { { \cos } ^ 2 } x } } } = \frac { 1} { 4 } \int { \frac { { \left ( { { { \sin } ^ 2 } x + { { \cos } ^ 2 } x } \right ) d x } } { { { \sin ^ 2 } x { { \cos } ^ 2 } x } } } = \frac { 1 } { 4 } \int { \left ( { \frac { 1 } { { { { \cos } ^ 2 } x } } + \frac { 1 }{ { { \sin ^ 2 } x } } } \right ) d x } \\ & = \frac { 1 } { 4 } \int { { { \sec } ^ 2 } x d x } + \frac { 1 } { 4 } \int { { \csc ^ 2 } x d x } = \frac { 1 } { 4 } \tan x - \frac { 1 } { 4 } \cot x + C = \frac { 1 } { 4 } \left ( { \tan x - \cot x } \right )+ C \end {align} ∫ sin 2 2 x d x = 4 1 ∫ sin 2 x cos 2 x d x = 4 1 ∫ sin 2 x cos 2 x ( sin 2 x + cos 2 x ) d x = 4 1 ∫ ( cos 2 x 1 + sin 2 x 1 ) d x = 4 1 ∫ sec 2 x d x + 4 1 ∫ csc 2 x d x = 4 1 tan x − 4 1 cot x + C = 4 1 ( tan x − cot x ) + C
جمعبندی
در این آموزش از مجله فرادرس، با مهمترین قوانین انتگرال و انتگرال گیری آشنا شدیم و مثالهایی از آن را حل کردیم.