معادلات ژنراتور سنکرون – به زبان ساده

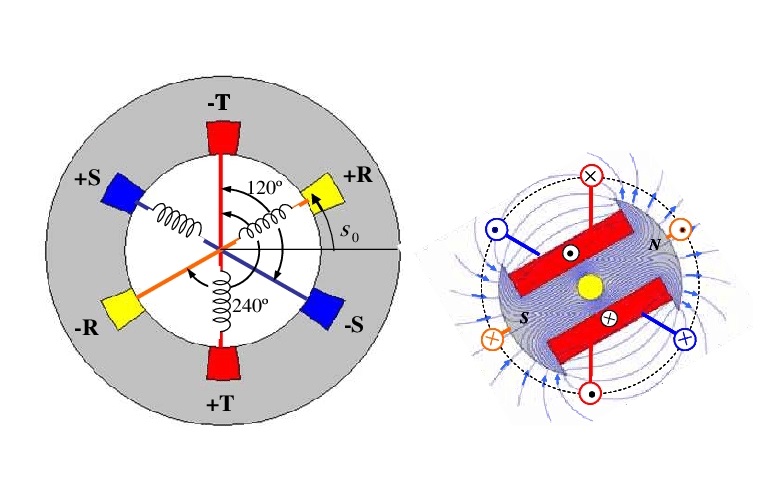
ژنراتورهای سنکرون، از اجزای اصلی سیستم قدرت هستند که در نیروگاه‌های متداول تولید برق وجود داشته و بخش بزرگی از برق مورد نیاز ما را تامین می‌کنند. این تجهیزات الکتریکی، توانی با فرکانس ثابت تولید می‌کنند و می‌توانند در ضریب توان پیش‌فاز و پس‌فاز کار کنند. در این آموزش، روابط و معادلات مربوط به مدار معادل ژنراتور سنکرون را بررسی می‌کنیم.

توان تحویلی ماشین

شکل ۱، نمودار فازوری یک ژنراتور سنکرون را نشان می‌دهد. با توجه به این شکل، می‌توان معادله ولتاژ را به‌صورت زیر نوشت:

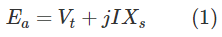
در شکل 1، ولتاژ ترمینال به‌عنوان فازور مرجع انتخاب شده است. زاویه بین ولتاژ ترمینال و ولتاژ تولیدی، زاویه توان است که با $$\delta$$ مشخص می‌شود.

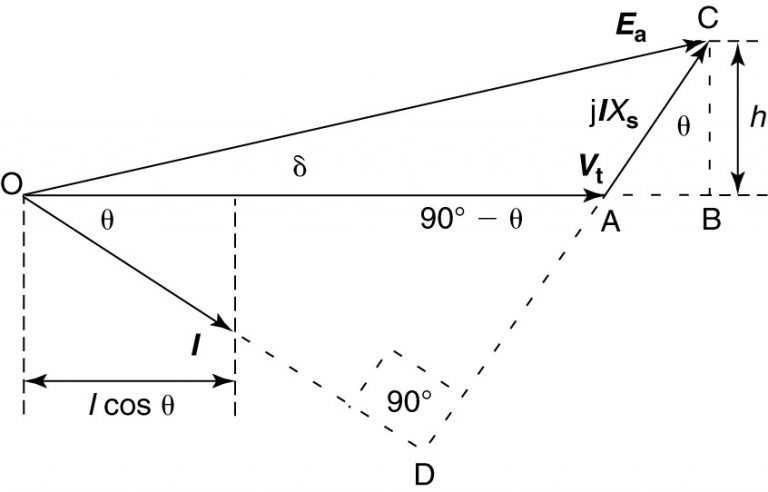
جریان در شکل 1، به‌صورت اختیاری به‌اندازه $$\theta$$ پس‌فاز انتخاب شده است، اما همه نتایجی که به‌دست خواهیم آورد، مستقل از ضریب توان است.

عبارت دوم سمت راست معادله (۱)، دارای ضریب j است که عددی مختلط بوده و اندازه آن برابر 1 و زاویه‌اش 90 درجه است. بنابراین، وقتی جریان را در jXs ضرب کنیم، فازور jlXs، جریان را به‌اندازه 90 درجه جلو می‌اندازد.

همان‌طور که در شکل 1 نشان داده شده، تقاطع امتداد فازور جریان با امتداد فازور $$jlX_S$$، یک زاویه قائمه است. این موضوع، یک راه ساده برای تشکل نمودار فازور است. بعد از آنکه ولتاژ ترمینال و جریان رسم شد، مثلث قائم‌الزاویه OAD تشکیل شده و خط DA جهت افت ولتاژ راکتانس ژنراتور را تعیین می‌کند.

مثلث OAD، قائم‌الزاویه است، بنابراین زاویه OAD برابر ($$90^\circ-\theta$$) است. با رسم یک خط از راس C که عمود بر امتداد بردار ولتاژ (خط AB) است، مثلث قائم‌الزاویه دیگری تشکیل می‌شود (ABC) که از نظر هندسی شبیه مثلث OAD است، زیرا دو ضلع آن‌ها با هم متقاطع است. بنابراین، زاویه ABC، برابر زاویه ضریب توان ($$\theta$$) است.

ضلع BC مثلث ABC‌، ارتفاع ولتاژ تولیدی روی ولتاژ ترمینال است که با h نشان داده شده است. اندازه h، تنها بر اساس جریان مثلث ABC محاسبه نمی‌شود و برحسب ولتاژ تولیدی است، زیرا مثلث OBC نیز قائم‌ازاویه است. در عمل،

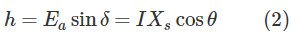
برای ولتاژ ترمینال و جریان شکل 1، می‌توانیم توان تحویلی هر فاز ماشین را با استفاده از فرمول توان محاسبه کنیم:

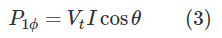
از معادله (2) می‌توانیم $$l\cos \theta$$ را برحسب ولتاژ تولیدی و زاویه توان $$\delta$$ به‌دست آوریم. با جایگذاری نتایج در معادله (۳)‌، داریم:

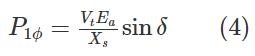
از آن‌جایی که توان سه‌فاز است، فرمول نهایی محاسبه توان به‌صورت زیر خواهد بود:

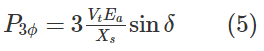
معادله (۵)، یک معادله بسیار مهم برای ژنراتور سنکرون است، زیرا توان تحویلی را با توان تولیدی و ولتاژ ترمینال و زاویه بین آن‌ها مرتبط می‌کند. این معادله به‌خوبی نشان می‌دهد که چرا به $$\delta$$‌ زاویه توان گفته می‌شود.

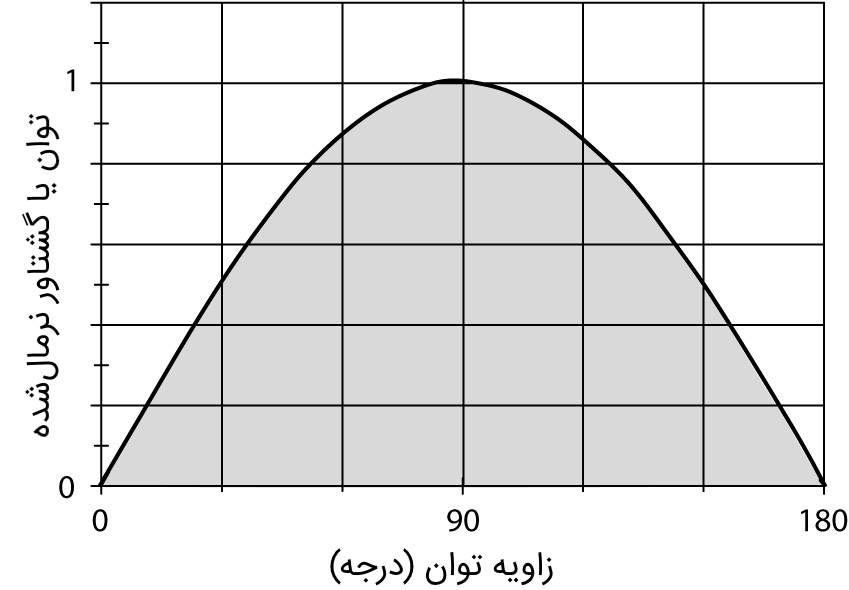
شکل 2، نمودار نرمال شده معادله (5) را نشان می‌دهد. توان تحویلی ماشین، با سینوس زاویه توان تغییر می‌کند.

افزایش زاویه توان تا 90 درجه، مقدار توان تحویلی ماشین را زیاد می‌کند. اگر زاویه توان، بیشتر از 90 درجه شود، ماشین توان کمتری را تحویل خواهد داد. اگر در این حالت بار بیشتری از ماشین کشیده شود، سبب می‌شود میدان رتور، از سنکرون بودن با میدان چرخان استاتور درآید و در نتیجه، سبب عملکرد ناپایدار ماشین خواهد شد. به این حالت، لغزش قطب (pole slipping) می‌گویند. لغزش قطب می‌تواند برای سنکرون بودن ماشین بسیار خطرناک باشد.

توان را می‌توان به‌کمک سرعت زاویه‌ای با گشتاور مرتبط کرد:

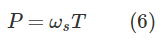
بنابراین، گشتاور الکترومغناطیسی ماشین، تابعی از زاویه توان است و حداکثر مقدار گشتاور ماشین در زاویه توان 90 درجه رخ می‌دهد (با فرض اینکه ولتاژهای تولیدی و ترمینال ثابت نگه داشته شوند).

مشابه فرمول‌های (2) تا (5)، توان راکتیو تولیدی یا مصرفی توسط ماشین، با رابطه زیر قابل محاسبه است:

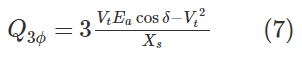
توان و گشتاور در ژنراتور قطب برجسته

توان و گشتاور محاسبه شده از معادلات (۵) و (۶)، نتیجه تعاملات میدان‌های مغناطیسی رتور و استاتور است. این تعاملات، در همه انواع ماشین‌های سنکرون وجود دارد که گاهی توان آهن‌ربا یا توان مغناطیسی نامیده می‌شود.

فیلم آموزش دینامیک سیستم های قدرت ۱ در فرادرس

کلیک کنید

در یک ماشین سنکرون استوانه‌ای، همه توان و گشتاور با توان آهن‌با به‌وجود می‌آید، در حالی که در یک ماشین قطب برجسته، سازوکار دیگری برای ایجاد گشتاور وجود دارد.

همان‌گونه که قبلاً بحث شد، فاصله هوایی یک ماشین قطب برجسته، یکنواخت نیست و این بدین معنی است که رلوکتانس فاصله هوایی، تابعی از موقعیت رتور است. بنابراین، ماشین سنکرون قطب برجسته را نمی‌توان با یک راکتانس سنکرون منحصر به فرد مدل کرد. بلکه، دو مقدار برای مدل کردن آن وجود دارد: راکتانس محور مستقیم ($$X_d$$) و راکتانس محور عمودی ($$X_q$$).

شار مغناطیسی، همیشه مسیری را برای عبور انتخاب می‌کند که رلوکتانس پایینی داشته باشد،‌ بنابراین، اگر میدان در ماشین قطب برجسته از بین برود، نیرویی وجود خواهد داشت که سعی می‌کند محور مستقیم رتور را با میدان مغناطیسی گردان تنظیم کند. بنابراین، گشتاور رلوکتانسی در ماشین سنکرون قطب برجسته خواهیم داشت که با توجه به معادله (۶)، توان اضافه‌ای تولید می‌کند.

توجه کنید که دو راه برای به‌دست آوردن مسیری با رلوکتانس کم در ماشین سنکرون قطب برجسته وجود دارد. به این معنی که می‌توان رتور را 180 درجه الکتریکی چرخاند، به‌طوری که هنوز مسیری با رلوکتانس کم وجود داشته باشد. در واقع، گشتاور و توان رلوکتانسی، به‌عنوان تابعی از دو زاویه توان تغییر می‌کنند. در استخراج رابطه توان یک ژنراتور سنکرون قطب برجسته، از همین واقعیت استفاده می‌شود. رابطه توان در ژنراتور سنکرون قطب برجسته به‌صورت زیر است:

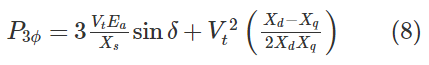
جمله اول سمت راست معادله (۸)، توان مغناطیسی و جمله دوم، توان رلوکتانسی است.

توجه کنید که در ماشین رتور استوانه‌ای، راکتانس محورهای مستقیم و عمودی برابر است. بنابراین، توان رلوکتانسی صفر است و و معادله (۸) به معادله (۵) تبدیل خواهد شد.

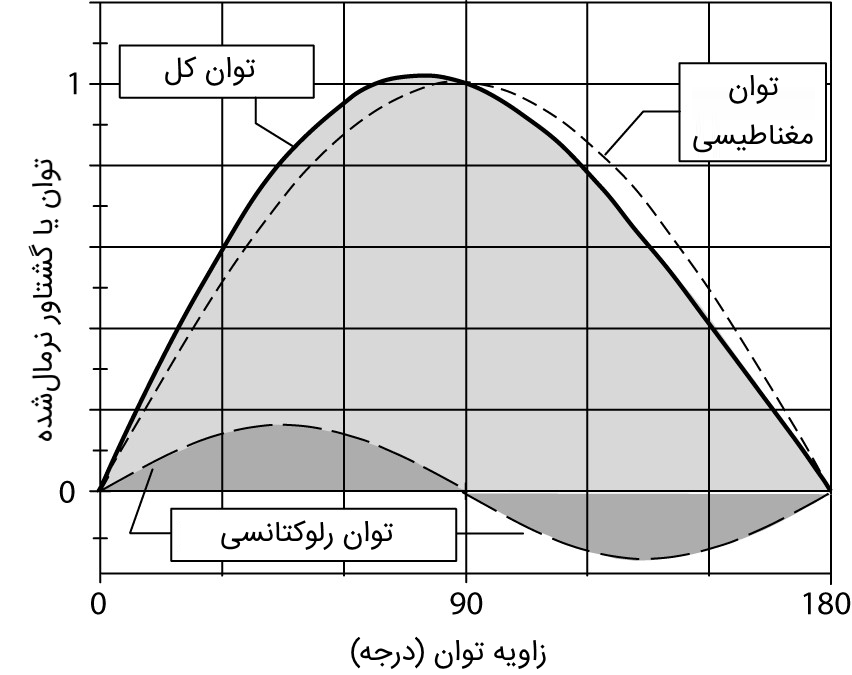
شکل 3، نمودار توان مغناطیسی، توان رلوکتانسی و توان کل یک رتور قطب برجسته را نشان می‌دهد. پیک توان و گشتاور رلوکتانسی، در زوایه توان $$45^\circ$$ اتفاق می‌افتد که سبب یک جابه‌جایی در حد پایداری ماشین خواهد شد. در این حالت، توان رلوکتانسی 15 درصد توان مغناطیسی است و حداکثر توان، در زاویه توان $$11^\circ$$ رخ می‌دهد.

در آموز‌ش‌های آینده، درباره سایر مباحث مربوط به ماشین‌های سنکرون بحث خواهیم کرد.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی قدرت
• مجموعه آموزش‌های مهندسی برق
• مجموعه آموزش‌های دروس مهندسی برق
• آموزش نرم افزار Adams Machinery برای مدلسازی سیستم های انتقال قدرت

^^