انرژی کرنشی در مواد الاستیک خطی — آموزش جامع

انرژی کرنشی یکی از مفاهیم اصلی در مکانیک کاربردی است. اصول مرتبط با این مفهوم به طور گسترده برای تعیین رفتار سازه‌ها در شرایط بارگذاری استاتیک و دینامیک مورد استفاده قرار می‌گیرد. در این مقاله، با در نظر گرفتن بارگذاری محوری در شرایط استاتیک، به معرفی انرژی کرنشی الاستیک و پلاستیک، انرژی کرنشی در مواد الاستیک خطی، انرژی کرنشی در میله‌های غیر یکنواخت و چگالی انرژی کرنشی خواهیم پرداخت. در انتها نیز چندین مثال کاربردی را برای شما ارائه خواهیم کرد.

مفاهیم اولیه انرژی کرنشی

برای آشنایی با مفاهیم اولیه انرژی کرنشی، یک میله منشوری با طول L را در نظر بگیرید که تحت نیروی کششی P قرار گرفته است (شکل زیر). فرض می‌کنیم که میزان بار اعمال شده به آرامی و به تدریج از 0 تا مقدار حداکثری P افزایش می‌یابد.

به این نوع بارگذاری، «بارگذاری استاتیک» (Static Loading) گفته می‌شود؛ چراکه عوامل دینامیک یا داخلی بر روی فرآیند بارگذاری تأثیری نمی‌گذارند. با شروع بارگذاری، طول میله به تدریج افزایش می‌یابد و هم‌زمان با اعمال بار P، تغییر طول میله نیز به مقدار حداکثری δ می‌رسد. پس از این فرآیند، میزان بار و تغییر طول ثابت باقی می‌ماند.

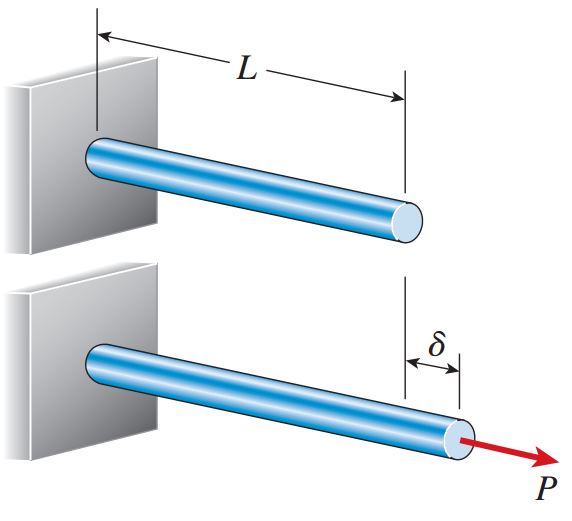
در طول فرآیند بارگذاری، بار P به آرامی درون δ حرکت می‌کند و مقدار مشخصی کار مکانیکی انجام می‌دهد. به منظور ارزیابی کار انجام شده در این مسیر می‌توانیم از رابطه معروف نیرو ضربدر فاصله (W=fx) استفاده کنیم. اگرچه، در مسئله‌ای که ما با آن سر و کار داریم، مقدار نیرو از 0 تا P تغییر می‌کند.

برای تعیین کار انجام شده در این نوع بارگذاری، باید نحوه تغییرات نیرو را مشخص کنیم. رسم منحنی بار-جابجایی، یکی از روش‌های موجود برای کسب اطلاعات مورد نیاز و محاسبه کار انجام شده است (شکل زیر). محور عمودی این منحنی بار محوری و محور افقی آن تغییر طول ناشی از اعمال بار را نمایش می‌دهد. شکل منحنی نیز به خواص ماده مورد آزمایش بستگی دارد.

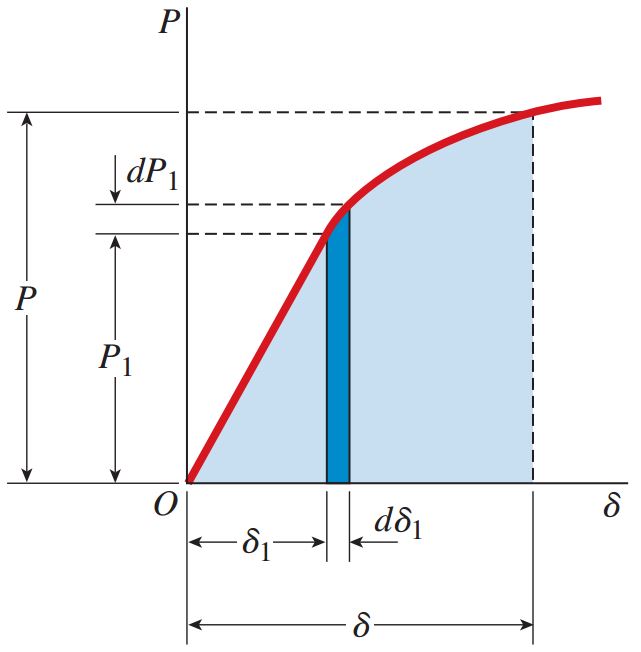
به منظور تعیین کار انجام شده، در ابتدا بار فرضی P₁ را بین مقادیر 0 تا P بر روی محور عمودی منحنی بار-جابجایی در نظر می‌گیریم. سپس، تغییر طول ناشی از اعمال بار P₁ را با عنوان δ₁ بر روی محور افقی علامت مشخص می‌کنیم. افزایش باری به اندازه dP₁ افزایش طولی به اندازه dδ₁ را در پی خواهد داشت. کار انجام شده در حین افزایش طول dδ₁ با حاصل‌ضربِ بار در مسیر حرکت (P₁dδ₁) برابر است. ستون پررنگ در منحنی بالا، کار انجام شده را نمایش می‌دهد. به این ترتیب، با جمع کردن تمام ستون‌های زیر منحنی بار-جابجایی، کار انجام شده در حین بارگذاری از نقطه 0 تا P به دست می‌آید:

از نظر هندسی، میزان کار انجام شده با مساحت سطح زیر منحنی بار-جابجایی برابر است. هنگام اعمال بار بر روی میله، کرنش‌هایی درون آن به وجود می‌آیند. وجود این کرنش‌ها، سطح انرژی میله را افزایش می‌دهد. میزان انرژی جذب‌شده توسط میله در حین فرآیند بارگذاری با عنوان «انرژی کرنشی» (Strain Energy) شناخته می‌شود. بر اساس اصل بقای انرژی، اگر هیچ مقداری از انرژی در حین بارگذاری به صورت گرما به سیستم اضافه یا از آن کم نشود، انرژی کرنشی با کار انجام شده برابر خواهد بود. بنابراین:

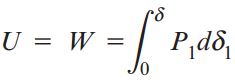
U: انرژی کرنشی

گاهی اوقات، از انرژی کرنشی با عنوان «کار داخلی» (Internal Work) یاد می‌شود. این عنوان، بین مفاهیم انرژی کرنشی و کار خارجی انجام شده تمایز ایجاد می‌کند. واحد کار و انرژی یکسان است. در سیستم SI، کار و انرژی با واحد ژول (J) بیان می‌شوند. این واحد برابر با یک نیوتن متر است (1J=1N.m). در سیستم آمریکایی، کار و انرژی با واحد فوت-پوند (ft-lb)، فوت-کیلو پوند (ft-k)، اینچ-پوند (in-lb) و اینچ-کیلو پوند (in-k) بیان می‌شوند.

انرژی کرنشی الاستیک و غیر الاستیک

اگر نیروی P به آرامی از روی ماده برداشته شود، طول نمونه کاهش خواهد یافت. در صورتی که ماده در ناحیه الاستیک قرار داشته باشد، طول آن به مقدار اولیه بازمی‌گردد. از سوی دیگر، در صورت عبور ماده از ناحیه الاستیک و قرارگیری در ناحیه پلاستیک، مقداری تغییر شکل دائمی درون آن باقی می‌ماند. در هر دو حالت، انرژی کرنشی به صورت کار بازیابی می‌شود. برای درک بهتر این رفتار، منحنی بار-جابجایی زیر را در نظر بگیرید.

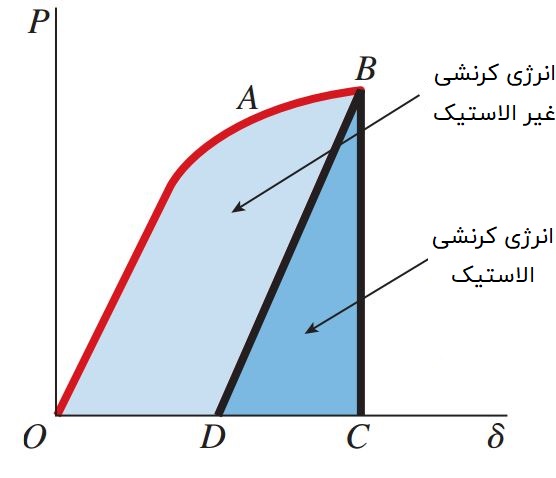
در حین بارگذاری، کار انجام شده با مساحت سطح زیر منحنی (مساحت OABCDO) برابر است. اگر نقطه B بیشتر از حد الاستیک باشد، منحنی بار-جابجایی مسیر BD را در هنگام باربرداری طی خواهد کرد. در این صورت، تغییر شکلی به اندازه OD درون ماده باقی می‌ماند. به انرژی کرنشی بازیابی‌شده در هنگام باربرداری، «انرژی کرنشی الاستیک» (Elastic Strain Energy) گفته می‌شود. در منحنی زیر، مقدار انرژی کرنشی الاستیک توسط مثلث BCD نمایش داده شده است. ناحیه OABDO، انرژی از دست رفته در طی فرآیند تغییر شکل دائمی نمونه را نشان می‌دهد. این انرژی با عنوان «انرژی کرنشی غیر الاستیک» (Inelastic Strain Energy) شناخته می‌شود.

طراحی اکثر سازه‌ها با فرض قرارگیری ماده در ناحیه الاستیک صورت می‌گیرد. نقطه A در منحنی بالا را به عنوان حد الاستیک در نظر بگیرید. تا زمانی که بار اعمال شده پایین‌تر از این نقطه باشد، انرژی کرنشی در حین باربرداری به طور کامل بازیابی خواهد شد. به علاوه، هیچ تغییر شکل دائمی در ماده باقی نخواهد ماند. بنابراین، ماده در این شرایط همانند یک فنر الاستیک، انرژی کرنشی را در حین بارگذاری و باربرداری، به ترتیب ذخیره و آزاد می‌کند.

انرژی کرنشی در مواد الاستیک خطی

میله‌ای را در نظر بگیرید که رفتار ماده تشکیل‌دهنده آن از قانون هوک پیروی می‌کند و منحنی بار-جابجایی آن به صورت یک خط راست است (شکل زیر). در این میله، انرژی کرنشی ذخیره شده از رابطه زیر محاسبه می‌شود:

رابطه بالا، مساحت مثلث OAB را نمایش می‌دهد.

رابطه بین بار P و تغییر طول δ برای میله‌ای از جنس یک ماده الاستیک خطی به صورت زیر نوشته می‌شود:

با ادغام دو رابطه بالا می‌توانیم انرژی کرنشی یک میله الاستیک خطی را به صورت دو معادله زیر بیان کنیم:

یا

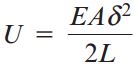
P: بار اعمال شده؛ L: طول میله؛ E: مدول الاستیسیته؛ A: مساحت سطح مقطع میله؛ δ: تغییرات طول میله

معادله اول، انرژی کرنشی را به صورت تابعی از بار و معادله دوم، انرژی کرنشی را به صورت تابعی از تغییر شکل نمایش می‌دهد. در صورت ثابت بودن میزان بار، انرژی کرنشی در میله‌های بلند بیشتر از میله‌های کوتاه است؛ چراکه در میله‌های بلند، مواد بیشتری در معرض ایجاد کرنش قرار می‌گیرند.

در طرف مقابل، افزایش مدول الاستیسیته و یا افزایش مساحت سطح مقطع میله باعث کاهش انرژی کرنشی می‌شود؛ زیرا افزایش این پارامترها، میزان کرنش را کاهش می‌دهد. برای درک بهتر این موارد می‌توانید به مثال‌های انتهای مقاله مراجعه کنید. سختی یک میله منشوری با استفاده از رابطه EA/L محاسبه می‌شود. با جایگذاری سختی فنر (k) به جای سختی میله منشوری در معادلات بالا، روابط انرژی کرنشی برای یک فنر الاستیک خطی به دست می‌آیند:

یا

انرژی کرنشی در میله‌های غیر یکنواخت

میزان انرژی کرنشی کل در میله‌های چندبخشی از حاصل جمع انرژی کرنشی هر بخش به دست می‌آید. شکل زیر را به عنوان یک مثال در نظر بگیرید. انرژی کرنشی این میله با جمع انرژی کرنشی در بخش‌های AB و BC برابر است.

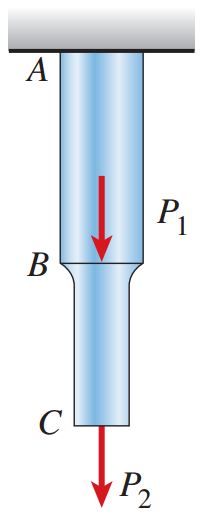
میله‌ای با دو بخش منشوری که تحت نیروهای محوری قرار گرفته است. مساحت سطح مقطع هر بخش با بخش دیگر متفاوت است.

رابطه ریاضی این مفهوم (برای رفتار خطی و غیر خطی) به صورت زیر بیان می‌شود:

U: انرژی کرنشی کل؛ U_i: انرژی کرنشی بخش i ام؛ n: تعداد بخش‌های میله

اکنون فرض کنید که ماده تشکیل‌دهنده میله دارای رفتار الاستیک خطی بوده و مقدار نیروی محوری در درون هر بخش ثابت است. با در نظر گرفتن این فرض و قرار دادن رابطه انرژی کرنشی یک میله الاستیک خطی در فرمول بالا می‌توانیم انرژی کرنشی بخش‌های مختلف میله را محاسبه کنیم:

N_i: نیروی محوری اعمال شده بر بخش i ام؛ L_i: طول بخش i ام؛ E_i: مدول الاستیسیته بخش i ام؛ A_i: مساحت سطح مقطع بخش i ام

شکل زیر، نمونه‌ای از یک میله غیر منشوری را نمایش می‌دهد که در معرض یک نیروی محوری با تغییرات پیوسته قرار گرفته است. برای تعیین انرژی کرنشی در این حالت می‌توانیم رابطه بالا را به فرم دیفرانسیلی تبدیل کنیم و سپس نسبت به تغییرات طول میله از آن انتگرال بگیریم:

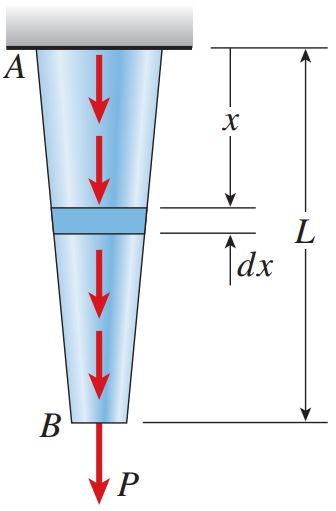
میله غیر منشوری تحت نیروی محوری با تغییرات پیوسته

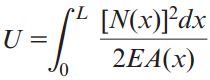
(N(x: نیروی محوری در فاصله x از انتهای میله؛ (A(x: مساحت سطح مقطع در فاصله x از انتهای میله

جابجایی‌های ناشی از اعمال یک بار منفرد

یکی از کاربردهای انرژی کرنشی در مسائل کاربردی، تعیین مقدار جابجایی سازه‌های الاستیک خطی در هنگام اعمال بار منفرد است. برای آشنایی با این روش، یک خرپای دو میله‌ای مطابق شکل زیر را در نظر بگیرید که در آن نیروی عمودی P به مفصل B وارد می‌شود. هدف ما در این مثال، تعیین میزان جابجایی عمودی δ در مفصل B است.

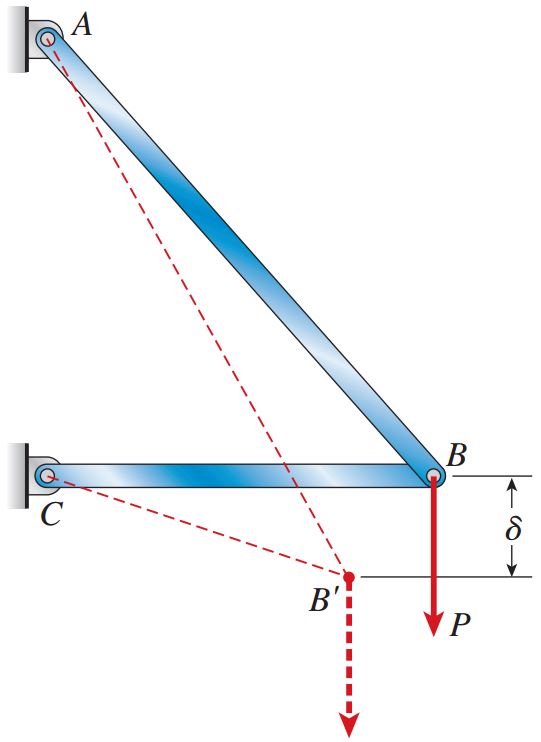
هنگام بارگذاری آرام بر روی خرپا و حرکت بار P در مسیر جابجایی عمودی δ، کار W به وجود می‌آید. توجه داشته باشید که در حرکت‌های افقی هیچ کاری انجام نمی‌شود. بنابراین، به دلیل خطی بودن منحنی بار-جابجایی، انرژی کرنشی U درون سازه ذخیره می‌شود. این انرژی با کار انجام شده در اثر اعمال بار برابر است:

با بازنویسی رابطه بالا نسبت به پارامتر جابجایی، به رابطه زیر می‌رسیم:

بر اساس این رابطه، در شرایط خاص امکان محاسبه جابجایی یک سازه به طور مستقیم و با استفاده از انرژی کرنشی آن وجود دارد. این شرایط عبارت‌اند از:

• رفتار سازه باید به صورت الاستیک خطی باشد.
• سازه باید فقط تحت بار منفرد قرار داشته باشد.
• تنها جابجایی قابل اندازه‌گیری در این شرایط، جابجایی ناشی از اعمال بار است. این جابجایی باید با بار اعمال شده هم‌راستا بوده و در نقطه اعمال بار قرار گرفته باشد.

با توجه به موارد فوق، کاربرد این روش برای تعیین جابجایی‌های یک سازه بسیار محدود می‌شود. علاوه بر این، این روش شاخص خوبی برای نمایش اهمیت بالای مبحث انرژی کرنشی در مکانیک سازها نیست اما می‌توان آن را به عنوان یکی از کاربردهای انرژی کرنشی در نظر گرفت.

چگالی انرژی کرنشی

برای راحتی کار در بسیاری از مسائل، به جای انرژی کرنشی از کمیت دیگری به نام «چگالی انرژی کرنشی» (Strain Energy Density) استفاده می‌شود. این کمیت معادل انرژی کرنشی بر واحد حجم است. برای تعیین چگالی انرژی کرنشی می‌توان از روابط انرژی کرنشی یک میله منشوری استفاده کرد.

به دلیل یکنواخت بودن توزیع انرژی کرنشی درون یک میله منشوری، چگالی آن از تقسیم انرژی کرنشی (U) بر حجم میله (A*L) به دست می‌آید. چگالی انرژی کرنشی با حرف u نمایش داده می‌شود. رابطه ریاضی این کمیت به صورت زیر است:

یا

با جایگذاری تنش σ به جای P/A و کرنش ε به جای δ/L در رابطه بالا، خواهیم داشت:

یا

روابط بالا برای محاسبه چگالی انرژی کرنشی مواد الاستیک خطی بر اساس مقادیر تنش σ یا کرنش ε مناسب هستند. در واقع، این روابط مساحت مثلث تشکیل‌شده در ناحیه زیر منحنی تنش-کرنش برای یک ماده الاستیک خطی را نمایش می‌دهند. در نظر داشته باشید که چگالی انرژی کرنشی در شرایطی که مواد از قانون هوک پیروی نمی‌کنند نیز با مساحت سطح زیر منحنی تنش-کرنش برابر است. در این مواد، مساحت سطح زیر منحنی برای هر ماده بخصوص به صورت جداگانه محاسبه می‌شود.

چگالی انرژی کرنشی در سیستم SI با واحد ژول بر متر مکعب (J/m³) و در سیستم آمریکایی با واحد فوت-پوند بر فوت مکعب، اینچ-پوند بر اینچ مکعب و واحدهای مشابه دیگر بیان می‌شود. از آنجایی که 1J=1N.m، با جایگذاری N.m در J/m³ به N/m² می‌رسیم. N/m² یا همان Pa، واحد تنش در سیستم SI است. به این ترتیب، چگالی انرژی کرنشی را می‌توان بر حسب واحدهای تنش نظیر پاسکال یا پوند بر اینچ مربع نیز بیان کرد.

میزان چگالی انرژی کرنشی یک ماده در حد تناسب، «ضریب فنریت» (Modulus of Resilience) نام دارد. ضریب فنریت با مساحت سطح زیر منحنی تا حد الاستیک برابر است. این ضریب، قابلیت جذب و آزادسازی انرژی کرنشی در محدوده الاستیک را نمایش می‌دهد. ضریب فنریت از طریق رابطه زیر محاسبه می‌شود:

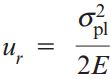
u_r: ضریب فنریت؛ σ_pl: مقدار تنش در حد تناسب

در ادامه به معرفی کمیت دیگری به نام «چقرمگی» (Toughness) می‌پردازیم. این کمیت قابلیت مواد در جذب انرژی کرنشی بدون رخ دادن شکست را نمایش می‌دهد. به مقدار چگالی انرژی کرنشی در نقطه شکست، «ضریب چقرمگی» (Modulus of Toughness) گفته می‌شود. این ضریب با مساحت کل سطح زیر منحنی تنش-کرنش برابر است. هر چه مقدار ضریب چقرمگی (u_t) بیشتر باشد، توانایی ماده در جذب انرژی کرنشی پیش از رخ دادن شکست بیشتر خواهد بود. از این‌رو، توجه به ضریب چقرمگی ماده در هنگام اعمال بارهای ضربه‌ای بسیار مهم است.

توجه: روابطی که در این مقاله به منظور محاسبه چگالی انرژی کرنشی معرفی شدند، تنها برای مواد تحت فشار یا کشش (تنش تک‌محوری) مناسب هستند.

نکات تکمیلی در رابطه با تحلیل انرژی کرنشی

با توجه به روابط به دست آمده برای انرژی کرنشی می‌توان مشاهده کرد که رابطه این کمیت با بارهای اعمال شده (حتی در مواد الاستیک خطی) به صورت خطی نیست. به این ترتیب، اگر سازه‌ای در معرض اعمال چندین بار قرار گرفته باشد، با جمع کردن انرژی کرنشی حاصل از هر بار نمی‌توان انرژی کرنشی کل را محاسبه کرد. به عنوان مثال، انرژی کرنشی کل در میله غیر منشوری زیر، از جمع انرژی کرنشی حاصل از بار P₁ و انرژی کرنشی حاصل از بار P₂ به دست نمی‌آید. در عوض، انرژی کرنشی کل در این میله باید با در نظر گفتن اعمال هم‌زمان تمام بارها محاسبه شود (مانند مثال 2 در انتهای مقاله).

در این مقاله، انرژی کرنشی را تنها برای سازه‌های تحت کشش در نظر گرفتیم. توجه داشته باشید که تمام مفاهیم و معادلات ارائه شده برای سازه‌های تحت فشار نیز قابل استفاده هستند. به علاوه، کار انجام شده توسط بار محوری (فارغ از کششی یا فشاری بودن)، مثبت است. به همین دلیل، انرژی کرنشی نیز همیشه مثبت خواهد بود. این مسئله را می‌توان در روابط مربوط به انرژی کرنشی میله‌های الاستیک خطی نیز مشاهده کرد. به دلیل وجود توان 2 بر روی پارامترهای بار اعمال شده و تغییر طول در این روابط، علامت انرژی کرنشی میله‌های الاستیک خطی همیشه مثبت خواهد بود.

انرژی کرنشی یکی از حالت‌های «انرژی پتانسیل» (Potential Energy) به شمار می‌رود زیرا این انرژی به موقعیت نسبی ذرات یا المان‌های سازنده یک عضو بستگی دارد. در هنگام فشرده شدن یک میله یا فنر، ذرات آن به یکدیگر نزدیک‌تر می‌شوند. در هنگام کشیده شدن یک میله یا فنر، ذرات آن از یکدیگر فاصله می‌گیرند. در هر دو حالت (کشش یا فشار)، انرژی کرنشی جسم نسبت به انرژی کرنشی پیش از بارگذاری افزایش می‌یابد.

مثال‌های کاربردی

برای درک بهتر کاربرد انرژی کرنشی و مفاهیم مرتبط با آن، به تشریح سه مثال کاربردی می‌پردازیم.

مثال 1

سه میله مدور با طول L و با شکل‌های متفاوت مانند شکل زیر را در نظر بگیرید. قطر این سه میله در نواحی مختلف و نحوه تغییرات آن‌ها در شکل نمایش داده شده است. هر سه میله تحت بار محوری P قرار دارند. با توجه به اطلاعات مسئله و با فرض رفتار الاستیک خطی، انرژی کرنشی ذخیره شده در این میله‌ها را با هم مقایسه کنید (از تأثیر تمرکز تنش و وزن میله‌ها صرف نظر شده است).

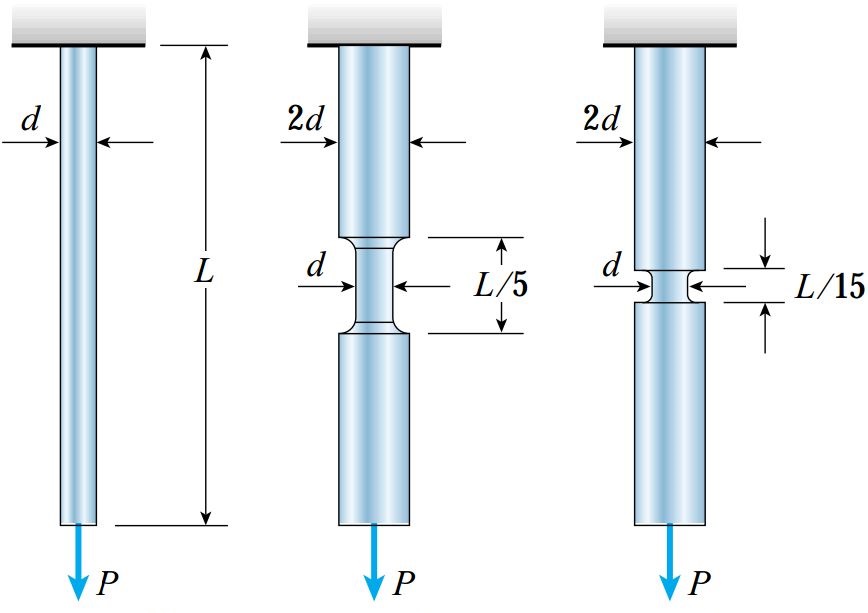
از آنجایی که قطر میله اول در طول آن تغییر نمی‌کند، انرژی کرنشی این میله (U₁) از طریق رابطه زیر به دست می‌آید:

در رابطه بالا، مساحت میله A=πd2/4 است.

قطر میله دوم، در بخش بالایی و پایینی آن برابر 2d و به اندازه L/5 در بخش مرکزی آن برابر d است. به این ترتیب، انرژی کرنشی کل در این میله (U₂) از حاصل جمع انرژی کرنشی در هر سه بخش به دست می‌آید:

این مقدار برابرِ 40 درصد انرژی کرنشی در میله اول است.

قطر میله سوم، در بخش بالایی و پایینی آن برابر 2d و به اندازه L/15 در بخش مرکزی آن برابر d است. به این ترتیب، انرژی کرنشی کل در این میله (U₃) نیز مانند میله دوم از حاصل جمع انرژی کرنشی در هر سه بخش به دست می‌آید:

 

مقدار انرژی کرنشی در این میله به 30 درصد انرژی کرنشی در میله اول تقلیل یافته است.

تحلیل نتایج: با مقایسه نتایج به دست آمده می‌توان نتیجه گرفت که افزایش سطح مقطع در بخشی از میله، مقدار انرژی کرنشی ذخیره شده را به طور قابل توجهی کاهش می‌دهد. اگر میزان کار انجام شده در هر سه میله برابر باشد، بیشترین مقدار تنش در میله سوم به وجود خواهد آمد. دلیل این موضوع، کمتر بودن ظرفیت ذخیره انرژی کرنشی در میله سوم نسبت به دیگر میله‌ها است.

در صورتی که طول بخش میانی میله سوم (با قطر d) کوچک‌تر شود، ظرفیت ذخیره انرژی این میله نسبت به قبل کاهش می‌یابد. به این ترتیب، در صورت وجود شیار بر روی یک میله، مقادیر کوچک کار نیز می‌توانند باعث ایجاد تنش‌های کششی بزرگ شوند. هر چه طول شیارها کوچک‌تر باشد، شرایط وخیم‌تر می‌شود.

در شرایط بارگذاری دینامیک که قابلیت جذب انرژی در آن یک مسئله مهم به حساب می‌آید، وجود شیار آسیب زیادی به ماده وارد می‌کند. در شرایط بارگذاری استاتیک، اهمیت تنش‌های ماکسیمم از قابلیت جذب انرژی بیشتر است. در این مثال، تنش ماکسیمم تمام میله‌ها یکسان است (σ_max=P/A). بنابراین، ظرفیت باربری هر سه میله در هنگام بارگذاری استاتیک برابر خواهد بود.

مثال 2

میله منشوری نمایش داده شده در شکل زیر را در نظر بگیرید. با توجه به شرایط بارگذاری الف) وزن میله و ب) وزن میله به علاوه بار P در انتهای آن، میزان انرژی کرنشی را محاسبه کنید.

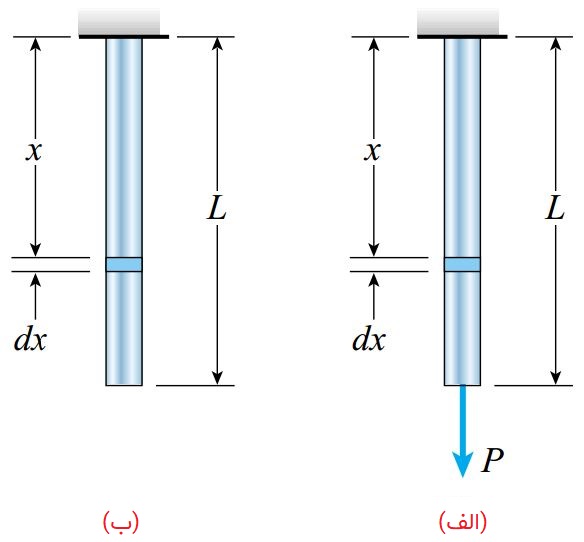
در حالت اول، میله تحت نیروی محوری متغیر قرار دارد. مقدار این نیرو در پایین‌ترین نقطه صفر و در بالاترین نقطه حداکثر است. برای تعیین این نیروی محوری، یک المان طول dx در فاصله x از بالای میله را در نظر می‌گیریم.

نیروی محوری داخلی اعمال شده بر روی این المان (N(x با وزن میله در پایین المان برابر است. به این ترتیب داریم:

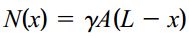
γ: وزن مخصوص ماده؛ A: مساحت سطح مقطع میله؛ L: طول میله؛ x: فاصله المان dx تا بالاترین نقطه میله

با جایگذاری رابطه بالا در معادله انرژی کرنشی برای میله تحت نیروی محوری با تغییرات پیوسته و انتگرال‌گیری از معادله به دست آمده، انرژی کرنشی کل قابل محاسبه خواهد بود:

در حالت دوم، میله علاوه بر وزن خود، تحت بار P نیز قرار گرفته است. در این حالت، نیروی محوری اعمال شده بر روی المان dx از حاصل جمع بار P و وزن میله در پایین المان به دست می‌آید:

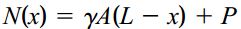
با جایگذاری رابطه بالا در برای میله تحت نیروی محوری با تغییرات پیوسته و انتگرال‌گیری از معادله به دست آمده می‌توانیم انرژی کرنشی کل را محاسبه کنیم:

 

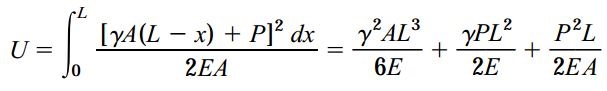
همان‌گونه مشاهده می‌کنید، عبارت اول در رابطه بالا با رابطه انرژی کرنشی برای میله آویزان تحت وزن خود (بخش اول مثال) و عبارت سوم با رابطه انرژی کرنشی برای میله تحت بار منفرد برابر است. اگرچه، عبارت دوم شامل هر دو پارامتر γ و P می‌شود. این موضوع نشان می‌دهد که عبارت دوم هم به وزن میله و هم به مقدار بار اعمال شده بستگی دارد. در نتیجه، مقدار انرژی کرنشی میله‌ای در هنگام اعمال دو بار مجزا، از جمع انرژی کرنشی حاصل از هر یک از بارها به دست نمی‌آید.

مثال 3

خرپای نمایش داده شده در شکل زیر را در نظر بگیرید. با فرض برابر بودن صلبیت محوری (EA) در هر دو عضو خرپا، میزان جابجایی مفصل B را تعیین کنید. توجه داشته باشید که تنها بار اعمال شه بر روی خرپا، بار عمودی P در مفصل B است.

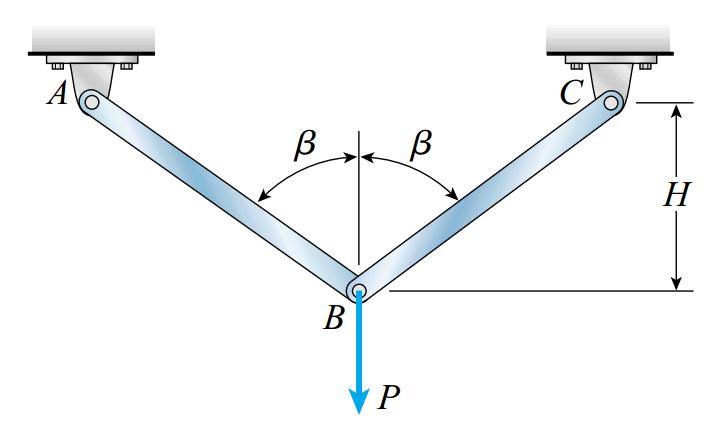
از آنجایی که تنها یک بار به خرپا اعمال می‌شود، برای تعیین جابجایی حاصل از اعمال آن بار می‌توان کار انجام شده را با انرژی کرنشی عضوها برابر قرار داد. بر اساس تعادل نیروهای اعمال شده بر روی مفصل B، نیروی محوری F در هر یک از عضوها به صورت زیر خواهد بود:

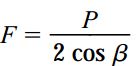
B: نصف زاویه داخلی بین عضوهای خرپا

با توجه به روابط مثلثاتی و هندسه خرپا، طول هر یک از میله‌ها برابر است با:

H: ارتفاع خرپا

اکنون می‌توانیم انرژی کرنشی هر دو میله را توسط رابطه زیر محاسبه کنیم:

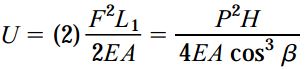
کار انجام شده توسط بار P نیز از طریق رابطه زیر به دست می‌آید:

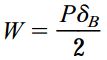
δ_b: جابجایی رو به پایین مفصل B

با برابر قرار دادن U و W و نوشتن معادله بر حسب δ_b خواهیم داشت:

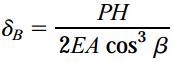
توجه داشته باشید که این رابطه جابجایی، تنها با استفاده از تعادل خرپا و انرژی کرنشی به دست آمده است. به این ترتیب، برای تعیین δ_b، نیازی به رسم نمودار جابجایی در مفصل B نخواهد بود.

^^