توزیع های آماری – مجموعه مقالات جامع وبلاگ فرادرس

بسیاری از پدیده‌های تصادفی در طبیعت هر چند تصادفی به نظر می‌رسند ولی دارای الگوی خاصی هستند. برای مثال پرتاب سکه و مشاهده نتیجه خط یا شیر، هر چند تصادفی است ولی می‌دانیم به شرط سالم بودن سکه، در ۵۰٪ موارد شیر و در ۵۰٪ موارد خط مشاهده خواهیم کرد. بنابراین قادر هستیم احتمال مشاهده هر یک از حالت‌های پدیده تصادفی را حدس بزنیم یا محاسبه کنیم. از طرف دیگر میانگین یا امید ریاضی نیز برای تعداد شیرهای مشاهده شده در ۱۰ بار پرتاب سکه، برابر با 5 است. به این معنی که به طور متوسط در ده بار پرتاب سکه ۵ بار شیر مشاهده خواهد شد. این اطلاعات از یک پدیده تصادفی (که به نظر می‌رسد باید تصادفی و غیرقابل پیش بینی باشد) برای آشنایی با آن پدیده بسیار موثر و مفید هستند. «توزیع های آماری» (Statistical Distributions) براساس قوانین احتمال، سعی دارند که خصوصیات و ویژگی‌های پدیده‌های تصادفی را نشان داده و به ما اطلاعاتی در مورد آن‌ها بدهند.

براساس تحقیقات و تلاش دانشمندان آمار و حتی حوزه‌های خارج از آمار، توزیع‌ های آماری مختلفی برای بیان خصوصیات پدیده‌های تصادفی ایجاد شده است. بنابراین اینطور به نظر می‌رسد که با مشاهده پدیده‌های تصادفی و جمع‌آوری داده‌های مربوطه، الگوی‌های ریاضی و احتمالاتی برای آن‌ها ایجاد شده است. سپس با مطالعه روی پدیده‌های دیگر ممکن است به الگو یا توزیع احتمالی یکسان یا متفاوتی رسید. به همین دلیل است که توزیع های آماری مختلف و متفاوتی ایجاد شده و مورد بررسی قرار گرفته است. هرگز نباید فراموش کرد که این توزیع‌ها براساس داده‌های تصادفی و به منظور نمایش ریاضی الگوی تصادفی آن‌ها ایجاد شده است.

در وبلاگ فرادرس، آموزش‌ها و مطالبی در زمینه معرفی توزیع‌های آماری و بررسی خصوصیات هر یک منتشر شده است. برای آگاهی و اطلاع بیشتر در این زمینه‌ها، این نوشتار، فهرستی از آن مطالب به همراه خصوصیات هر یک از توزیع‌‌ها را یادآور می‌شود.

توزیع های آماری برای متغیرهای تصادفی گسسته

همانطور که در دیگر نوشتارهای فرادرس گفته شد، متغیرهای تصادفی گسسته، دارای مجموعه مقادیری هستند که زیرمجموعه اعداد طبیعی است. این مجموعه را با نام تکیه‌گاه نیز می‌شناسند.

در متغیرهای تصادفی گسسته، تکیه‌گاه ممکن است متناهی و یا شمارش‌پذیر باشد. در فهرست زیر به بعضی از متغیرهای تصادفی گسسته به همراه توزیع آماری آن‌ها اشاره خواهیم داشت.

• توزیع برنولی (Bernoulli Distribution) که در آن به بررسی متغیر تصادفی حاصل از یک آزمایش برنولی پرداخته می‌شود. تکیه‌گاه یا مجموعه مقادیر این متغیر تصادفی دو حالت ۰ و ۱ را در بر می‌گیرد. بسیاری از متغیرها و توزیع‌های آماری گسسته برمبنای این توزیع و آزمایش تصادفی برنولی ساخته می‌شوند.
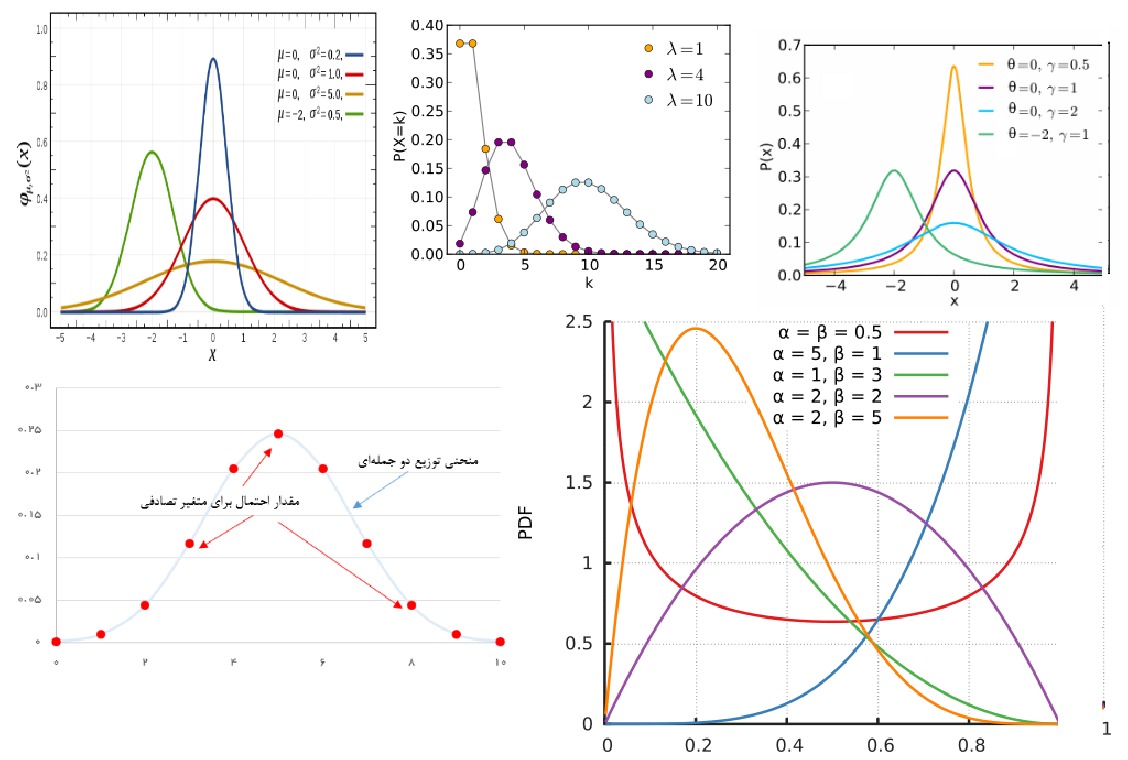
• توزیع دو جمله‌ای (Binomial Distribution) که براساس جمع متناهی از متغیرهای تصادفی برنولی مستقل ساخته می‌شود که احتمال موفقیت (مشاهده ۱) برایشان یکسان هستند. این توزیع یکی از کاربردی‌ترین توزیع‌های گسسته محسوب می‌شود. بطوری که در آزمون‌های نسبت از آن استفاده می‌شود.
• توزیع هندسی (Geometric Distribution) نیز براساس تکرار آزمایش برنولی ساخته می‌شود و احتمال رسیدن به اولین موفقیت را بررسی می‌کند. امید ریاضی و واریانس برای این متغیر تصادفی در مطلب فرادرس به همراه مثال‌های متعدد مورد بررسی قرار گرفته است.
• توزیع دو جمله ای منفی (Negative Binomial Distribution) که باز هم با توزیع برنولی مرتبط است از دیگر توزیع‌های گسسته است که در بحث تعیین حجم جامعه براساس یک نمونه کاربرد دارد. در مطلب فرادرس، این توزیع به همراه خصوصیاتش شرح داده شده است.
• توزیع فوق هندسی (Hyper Geometric Distribution) یکی از کاربردی‌ترین توزیع‌های آماری برای انجام آزمون‌های بررسی کنترل کیفی و بازرسی نمونه‌ای است. در این نوشتار به معرفی این توزیع و خصوصیاتش پرداخته‌ایم. همچنین مثال‌های مختلفی نیز برای کاربردهای آن بیان شده است.
• توزیع پواسن (Poisson Distribution) برای بیان پدیده‌های نادر کاربرد دارد. تابع توزیع، تابع احتمال، امید ریاضی و واریانس این متغیر تصادفی در این نوشتار فرادرس قابل مشاهده است. همچنین نحوه ارتباط این توزیع با توزیع دو جمله‌ای در آن شرح داده شده است. استفاده از مثال‌های متنوع و گوناگون از ویژگی‌های این مطلب است.
• توزیع چند جمله‌ای (Multinomial Distribution) را می‌توان حالت کلی‌تری برای توزیع دو جمله‌ای در نظر گرفت. اگر آزمایش برنولی را به شکلی تغییر داد که نتایج آزمایش تصادفی به k رده تعلق داشته باشند، توزیع چند جمله‌ای را می‌توان براساس آن ساخت. در این نوشتار به بررسی ویژگی‌های این توزیع به همراه یک مثال‌ کاربردی پرداخته‌ایم. همچنین نحوه شبیه‌سازی داده‌های توزیع چند جمله‌ای به کمک اکسل معرفی شده است.
• توزیع یکنواخت گسسته (Uniform Distribution) به عنوان ابزاری برای تولید اعداد تصادفی از اهمیت زیادی برخوردار است. همچنین از این توزیع برای برآورد تعداد تانک‌های دشمن براساس شماره سریال تانک‌های غنیمتی استفاده‌های زیادی در طی جنگ جهانی دوم شد. در این نوشتار خصوصیات این توزیع به همراه مثال‌هایی در این زمینه مورد بررسی قرار می‌گیرد.
• «توزیع بولتزمان» (Boltzmann Distribution)، در مکانیک آماری این توزیع که گاهی «توزیع گیبس» (Gibbs Distribution) نیز نامیده می‌شود، یک توزیع احتمال یا «اندازه احتمال» (Probability Measure) است و متغیر تصادفی آن دارای تکیه‌گاهی با مقادیر گسسته است. تابع احتمال در اینجا نشان می‌دهد که یک سیستم مکانیکی (یا ترمودینامیکی) با چه میزان احتمالی در «حالت» (state) خاصی قرار گرفته است.

توزیع های آماری برای متغیرهای تصادفی پیوسته

اگر تکیه‌گاه یا مجموعه مقدارهای یک متغیر تصادفی شامل اعداد حقیقی باشد، آن را پیوسته می‌نامند.

فیلم آموزش نمایش اطلاعات آماری و توزیع ها در متلب (رایگان) در فرادرس

کلیک کنید

در ادامه به لیستی از متغیرهای تصادفی پیوسته و توزیعشان اشاره می‌کنیم که در مطالب فرادرس به آن‌ها پرداخته‌ایم.

• توزیع نرمال (Normal Distribution) یکی از مهم‌ترین توزیع آماری محسوب می‌شود که کاربرد وسیعی در تحلیل داده‌ها دارد. در بیشتر روش‌های آماری پارامتری، فرض بر وجود توزیع نرمال برای جامعه آماری است. گاهی به آن  توزیع گوسی (Gaussian Distribution) یا توزیع زنگی‌ شکل (Bell-shape Distribution) نیز می‌گویند. در این نوشتار خصوصیات توزیع نرمال یک و چند متغیره مورد بررسی قرار گرفته است. مثال‌هایی برای حالت یک و دو متغیره نیز در این مطلب به چشم می‌خورد. همچنین تشریح قضیه حد مرکزی در این نوشتار قابل مطالعه است.
• توزیع t student نیز به عنوان ابزاری برای اجرای آزمون‌های آماری مورد استفاده است. تشریح خصوصیات این توزیع به همراه مثال‌های محاسباتی از خصوصیات این نوشتار محسوب می‌شود.
• توزیع F (فیشر- Fisher Distribution) در آزمون فرض مربوط به تحلیل واریانس کاربرد دارد. همچنین در تحلیل رگرسیونی برای آزمون مناسب بودن مدل از آماره‌ای با توزیع F استفاده می‌شود. در این مطلب توزیع F به همراه مثال‌هایی، معرفی و مورد بررسی قرار گرفته است.
• توزیع پارتو (Pareto Distribution) یکی از توزیع‌های آماری است که به بیان پدیده‌‌های تصادفی مرتبط با داده‌های مالی و جمعیتی می‌پردازد. در نوشتار فرادرس، این توزیع مطرح شده و کاربردهای آن در علوم مختلف با ذکر مثال‌های متنوعی مورد بازبینی قرار گرفته است. همچنین ارتباط این توزیع با اصل ۸۰-۲۰ یا قانون پارتو نیز از ویژگی‌های این نوشتار محسوب می‌شود.
• توزیع گاما و بتا (Gamma and Beta Distributions) در حوزه آمار بیز (Bayesian Statistics) به عنوان توزیع‌های پیشین به کار می‌روند. بنابراین آگاهی از ویژگی‌هایشان بخصوص در این زمینه مورد توجه است. در این نوشتار به بررسی این دو توزیع پرداخته و خصوصیات هر یک به همراه نحوه محاسبات تابع احتمال و توزیع احتمال معرفی شده است.
• توزیع کای ۲ (Chi Square) نیز با تکیه‌گاه و مجموعه مقدارهای مثبت برای پدیده‌هایی با این مجموعه مقادیر و البته چولگی زیاد مورد توجه است. آماره مربوط به «آزمون نیکویی برازش» (Goodness of Fit Test)نیز دارای توزیع کای ۲ است.
• توزیع نمایی (Exponential Distribution) می‌تواند قانون احتمال برای متغیر تصادفی مربوط به زمان رسیدن به اولین رخداد (موفقیت یا شکست) را نشان دهد. بنابراین در بیشتر موارد برای نشان دادن طول عمر بخصوص برای قطعات الکترونیکی از این توزیع استفاده می‌شود. خاصیت عدم حافظه یکی از خصوصیات جالب این توزیع است.
• توزیع یکنواخت (Uniform Distribution) از نوع پیوسته نیز یکی از مواردی است که در وبلاگ فرادس به آن پرداخته‌ایم. ارتباط این توزیع با دیگر توزیع‌های آماری در این نوشتار مورد بحث قرار گرفته است. همچنین تولید اعداد تصادفی از توزیع یکنواخت به کمک اکسل از مواردی است که در این مطلب وجود دارد.
• توزیع کوشی (Cauchy Distribution)، به عنوان یک توزیع دم سنگین، دارای خصوصیات جالبی است که می‌تواند به رخداد پدیده‌هایی بپردازد که دارای مقدارهای دورافتاده هستند. به همین منظور در این نوشتار فرادرس با این توزیع آشنا شده و خصوصیات آن مورد مانند ناموجود بودن میانگین و واریانس مورد بررسی قرار گرفته است.
• توزیع نرمال بریده شده (Truncated Normal Distribution)، به عنوان نوعی از توزیع نرمال است که از یک یا دو طرف محدود شده است. در مواردی که با داده‌های مثلا طول عمر مواجه هستیم از این توزیع می‌توان استفاده کرد. نوشتاری در وبلاگ فرادرس به این توزیع پرداخته شده و شیوه شبیه‌سازی داده‌های با این توزیع مورد بررسی قرار گرفته است.
• توزیع لاگ نرمال (Log-normal Distribution)، نیز یکی دیگر از انواع توزیع‌های استخراج شده از توزیع نرمال است. اگر متغیر تصادفی $$X$$ دارای توزیع لاگ نرمال باشد، آنگاه توزیع $$Y=\ln(X)$$ نرمال است.
• توزیع لاپلاس (Laplace Distribution)، به متغیر تصادفی می‌پردازد که از لحاظ ظاهری بسیار شبیه توزیع نرمال است با این تفاوت که به میانه داده‌ها به عنوان نقطه مرکزی توجه دارد. در توزیع نرمال این مرکز توجه به میانگین داده‌ها است.
• توزیع دریکله (Dirichlet Distribution)، مربوط به متغیر تصادفی چند متغیره است. تکیه‌گاه متغیر تصادفی با توزیع دریکله، در فاصله ۰ تا ۱ است. از طرفی باید مجموع این مقادیر نیز برابر با ۱ باشد. بنابراین با برداری تصادفی مواجه هستیم که دارای خصوصیات جالبی است.
• توزیع وایبل (Weibull Distribution)، یک متغیر تصادفی با مقادیر پیوسته است. تکیه‌گاه این متغیر تصادفی، اعداد حقیقی نامنفی است در نتیجه در مواردی که متغیر تصادفی مربوط به طول عمر باشد، می‌توان از این توزیع استفاده کرد.
• توزیع تصادفی رایلی (Rayleigh Distribution)، یکی توزیع آماری پیوسته (Continuous) است که تکیه‌گاه متغیر تصادفی آن، مقادیر نامنفی است. در حالت خاص این توزیع شبیه یک توزیع کای ۲ با دو درجه آزادی است. برای بیان خطا در دستگاه‌ها و پدیده‌های فیزیکی مثلا برآورد خطای دستگاه MRI از این توزیع استفاده می‌کنند.

عناوین مرتبط با توزیع‌های آماری

همچنین در فهرست زیر مطالبی از وبلاگ فرادرس دیده می‌شود که با توزیع‌های آماری و مباحث مرتبط با آن ارتباط دارند. خواندن این مطالب نیز برای آشنایی بیشتر با کاربرد توزیع‌های آماری مفید خواهد بود.

• آزمون‌ نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای2
• توزیع‌ های آماری و رسم نمودار تابع احتمال — با کدهای R
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده
• فاصله اطمینان (Confidence Interval) — به زبان ساده
• قانون پارتو (Pareto Law) — تعریف و کاربردهای آن

البته در آموزش‌های زیر، مطالبی که در بالا به آن‌ها پرداختیم، به صورت ویدئویی و به تفصیل توضیح داده شده‌اند که مشاهده آن‌ها نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• مجموعه آموزش‌های SPSS
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های نرم‌افزارهای آماری
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• فاصله اطمینان (Confidence Interval) — به زبان ساده

^^