توزیع بولتزمان در ترمودینامیک آماری | به زبان ساده

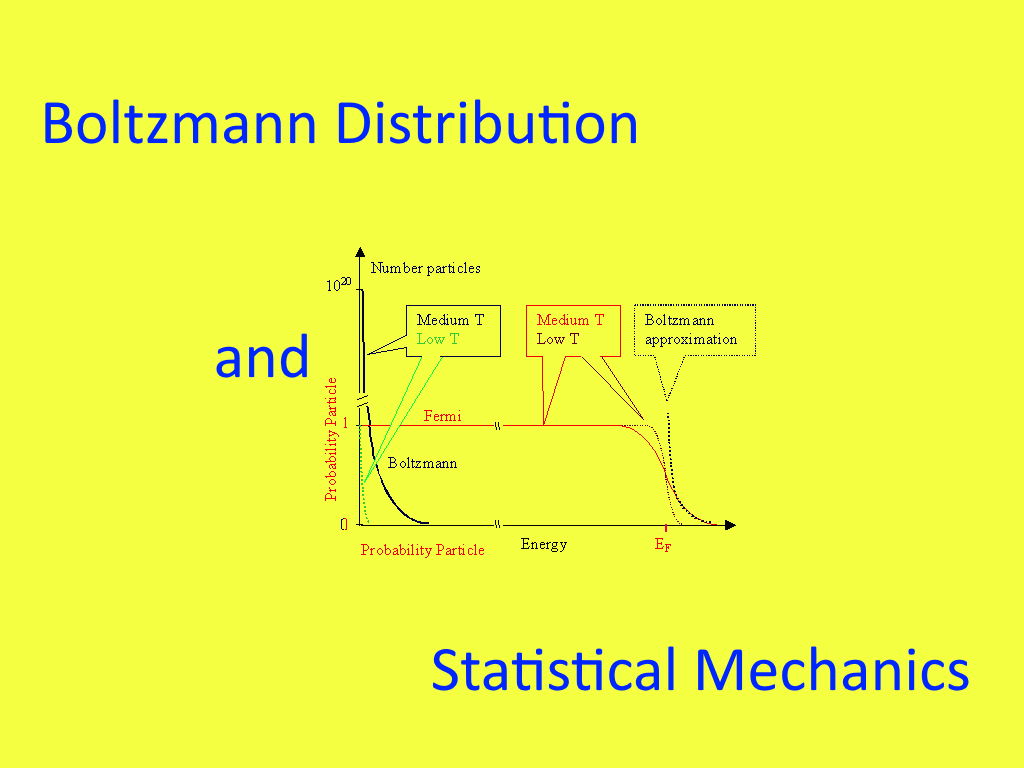
توزیع‌های آماری مرتبط با بیان رفتار داده‌های تصادفی هستند. البته این مقادیر تصادفی نیز دارای قواعدی هستند که مباحث مربوط به احتمال و توزیع آماری، به آن‌ها می‌پردازند. به این ترتیب متوجه می‌شویم که چه مقادیری احتمال رخداد بیشتری دارند و یا به طور مثال، انتظار داریم چه مقداری از آن‌ها را در صورت تکرار «آزمایش تصادفی» (Random Experiment)، مشاهده کنیم. یکی از توزیع‌های مهم و کاربردی، توزیع بولتزمان در «مکانیک آماری» یا «ترمودینامیک آماری» است. گاهی این توزیع به صورت «توزیع بولتزمن» نیز نوشته می‌شود. در این نوشتار از مجله فرادرس به علت استفاده از این توزیع بخصوص در ترمودینامیک آماری، به معرفی آن خواهیم پرداخت و خصوصیات آن را مورد بررسی قرار خواهیم داد.

به منظور آشنایی بیشتر با موضوع توزیع‌های آماری بهتر است مطالب دیگر مجله فرادرس با عنوان توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس و توزیع های پیوسته آماری و رابطه بین آنها — به زبان ساده را مطالعه کنید. همچنین خواندن دو نوشتار ترمودینامیک آماری — مبانی و مفاهیم به زبان ساده و مکانیک آماری (Statistical Mechanics) — به زبان ساده نیز خالی از لطف نیست.

توزیع بولتزمان در مکانیک آماری

در مکانیک آماری و شاخه احتمال در ریاضیات، «توزیع بولتزمان» (Boltzmann Distribution) یا «بولتزمن»، که گاهی «توزیع گیبس» (Gibbs Distribution) نیز نامیده می‌شود، یک توزیع احتمال یا «اندازه احتمال» (Probability Measure) است و شانس آن را نشان می‌دهد که یک سیستم در «حالت» (state) خاصی قرار گرفته باشد. البته حالت سیستم به عنوان تابعی از انرژی آن حالت و دمای سیستم در نظر گرفته و پارامترهای تابع احتمال را تشکیل می‌دهند. شکل یا فرمول تابع احتمال این توزیع با پارامترهای آن به صورت زیر بیان می‌شود.

$$ \large {\displaystyle p_{i} \propto e^{- {\dfrac {\varepsilon_{i}} {kT}}}} $$

واضح است که در آن $$p_i$$، احتمال بودن سیستم در حالت $$i$$ بوده و همچنین $$\varepsilon_i$$ نیز انرژی را در آن حالت بیان می‌کند. از طرفی $$kT$$ یک ثابت توزیع محسوب شده که نتیجه حاصل‌ضرب $$k$$ یعنی «ثابت بولتزمان» (Boltzmann’s constant) و «دمای ترمودینامیکی» (Thermodynamic Temperature) یعنی $$T$$ است. واضح است که نماد $$\textstyle {\propto }$$ هم، تناسب را نشان می‌دهد. به این ترتیب مشخص می‌شود که این احتمال به چه عواملی بستگی دارد.

به منظور ایجاد یک «توزیع احتمال» (Probability Distribution)، باید این تناسب به صورت یک تساوی نوشته شود. به این منظور معمولاً مقدار سمت راست تناسب را به مجموع کل حالت‌ها، تقسیم می‌کنند تا یک تابع احتمال حاصل شود. این موضوع را در ادامه مشاهده خواهید کرد.

اصطلاح «سیستم» (System) در اینجا معنای بسیار گسترده‌ای دارد، این عبارت می‌تواند از یک واحد اتمی تا یک سیستم ماکروسکوپی مانند مخزن ذخیره‌سازی گاز طبیعی را در بر گیرد. به این دلیل توزیع بولتزمان برای حل انواع بسیار گسترده‌ای از مسائل مورد استفاده قرار گرفته است. این توزیع نشان می‌دهد، حالت‌هایی که انرژی کمتری (به عنوان پیشامد تصادفی) دارند، همیشه احتمال اشغال شدن (یا رخ دادن) بالاتری نسبت به حالت‌های دیگر خواهند داشت.

نسبت احتمالات (نسبت بخت – Odd Ratio) دو حالت به عنوان «عامل بولتزمان» (Boltzmann Factor) یا «فاکتور بولتزمن» شناخته می‌شود و از نظر مشخصه، تنها به اختلاف انرژی حالت‌ها بستگی دارد. به این ترتیب رابطه زیر را خواهیم داشت.

$$ \large {\displaystyle {\dfrac {p_{i}}{p_{j}} = e^{\dfrac {\varepsilon_{j} – \varepsilon_{i}}{kT}}}} $$

تاریخچه توزیع بولتزمان

توزیع بولتزمان نام خود را از «لودویگ بولتزمان» (Ludwig Boltzmann) گرفته است. وی اولین بار این رابطه را در سال ۱۸۶۸ هنگامی که در حوزه مکانیک آماری گازها، تحقیق می‌کرد، مورد بررسی قرار داد و یک رابطه در مورد حالت تعادل حرارتی گازها ارائه نمود.

کار آماری بولتزمان در مقاله‌اش با نام «در مورد رابطه بین نظریه بنیادی دوم نظریه مکانیکی محاسبات گرما و احتمال در مورد شرایط تعادل حرارتی» (On the Relationship between the Second Fundamental Theorem of the Mechanical Theory of Heat and Probability Calculations Regarding the Conditions for Thermal Equilibrium) مورد توجه قرار گرفت.

توزیع ابداعی او، بعدها به طور گسترده، در شکل عمومی و مدرن آن، توسط «ویلارد گیبس» (Josiah Willard Gibbs) در سال ۱۹۰۲ مورد بررسی و به طور کامل، در «ترمودینامیک آماری» (Statistical Thermodynamic) و «مکانیک آماری» (Statistical Mechanics) استفاده شد.

«توزیع بولتزمن تعمیم یافته» (Generalized Boltzmann Distribution)، شرط لازم و کافی برای هم ارزی بین تعریف مکانیک آماری آنتروپی (فرمول آنتروپی گیبس $$ {\displaystyle S = -k_{\mathrm {B} } \sum_{i} p_{i} \log p_{i} }$$) و تعریف «ترمودینامیکی آنتروپی» یعنی رابطه ($$ {\displaystyle dS = {\dfrac {\delta Q_{\text{rev}}}{T}}} $$) به همراه «رابطه ترمودینامیکی بنیادین» (Fundamental Thermodynamic Relation) محسوب می‌شود.

نکته: توزیع بولتزمان نباید با «توزیع ماکسول–بولتزمان» (Maxwell–Boltzmann distribution) اشتباه گرفته شود. واضح است که توزیع بولتزمان، این احتمال را نشان می‌دهد که یک سیستم در حالت خاصی به عنوان تابعی از انرژی آن حالت باشد، در حالیکه توزیع ماکسول-بولتزمان، برای توصیف سرعت ذرات در گازهای ایده آل به کار می‌رود.

تابع توزیع بولتزمان

همانطور که گفته شد، توزیع بولتزمن یک توزیع احتمال است و باید به مانند آن‌ها نوشته شده و خصوصیاتش منطبق با آن‌ها باشد. از طرفی این تابع باید احتمال این که یک حالت خاص از سیستم اتفاق بیافتد را برحسب تابعی از انرژی و دمای آن حالت سیستم مشخص کند. به این ترتیب برای معرفی تابع احتمال در این توزیع، از رابطه زیر استفاده می‌شود.

$$ \large \displaystyle p_{i} = \dfrac {1}{Q} e^{- {\varepsilon }_{i}/kT} = \dfrac {e^{ -{\varepsilon }_{i} / kT}}{\sum_{j = 1}^{M} {e^{{\varepsilon }_{j} / kT}}} $$

که در آن $$p_i$$ احتمال در حالت $$i$$ و همچنین $$\varepsilon_i$$ نیز انرژی را در آن حالت مشخص می‌کند. از طرفی $$k$$ ثابت بولتزمن و $$T$$ نیز دمای سیستم و $$M$$ نیز تعداد کل حالت‌های قابل دسترس سیستم مورد نظر است. به این ترتیب مشخص است که متغیر تصادفی مربوط به توزیع بولتمن دارای یک توزیع گسسته است و مقادیر متغیر تصادفی یا تکیه‌گاه آن شامل اعداد صحیح مثبت یا اعداد طبیعی است.

عبارت گفته شده در بالا، با مفهوم احتمال براساس نسبت تعداد حالت‌های مطلوب به کل حالت‌ها، صدق می‌کند. مخرج این کسر یعنی $$Q$$ (که توسط برخی از نویسندگان توسط $$Z$$ نشان داده می‌شود) «تابع پارش» (Partition Function) یا بخش‌های کانونی است.

$$ \large \displaystyle Q = {\sum_{i = 1}^{M}{e^{ -{\varepsilon }_{i} / kT}}} $$

اما یک محدودیت نیز وجود دارد که مجموع احتمالات تمام حالت‌های در دسترس باید برابر با ۱ باشند. به این ترتیب تابع احتمال بولتزمان برای هر حالت از سیستم حاصل می‌شود. توزیع بولتزمان آنتروپی را به حداکثر می‌رساند، در نتیجه رابطه زیر برقرار است.

$$\large {\displaystyle H(p_{1}, p_{2}, \cdots ,p_{M}) = -\sum_{i = 1}^{M} p_{i} \log_{2}p_{i}} $$

البته باید به شرطی که به صورت $$\textstyle {\sum {p_{i} {\varepsilon }_{i}}}$$ در نظر گرفته می‌شود نیز توجه داشت. به این ترتیب حداکثر آنتروپی، برابر مقدار انرژی میانگین است که می‌تواند با استفاده از ضریب‌های لاگرانژ بدست آید.

«تابع پارش» را زمانی می‌توان محاسبه کرد که انرژی‌های حالت‌های قابل دسترسی در سیستم مورد بحث، مشخص باشند. برای اتم‌ها، مقادیر تابع پارتیشن را می‌توان در پایگاه داده طیف اتمی NIST یافت.

توزیع بولتمن نشان می‌دهد که حالت‌هایی که انرژی کمتری دارند همیشه احتمال رخ‌دادن بیشتری نسبت به حالت‌ها با انرژی بالاتر، دارند. همچنین این رابطه می‌تواند ارتباط بین احتمالات اشغال دو حالت را به ما بدهد. نسبت احتمالات برای حالت $$i$$ و $$j$$ به شکل زیر خواهد بود.

$$ \large \displaystyle {\dfrac {p_{i}} {p_{j}} = e^{({\varepsilon }_{j} – {\varepsilon }_{i}) / kT}}$$

که در آن $$p_i$$ احتمال حالت $$i$$ و $$p_j$$ نیز احتمال حالت $$j$$ است. مشخص است که $$\varepsilon_i$$ و $$\varepsilon_j$$ انرژی‌های مربوط به حالت‌های متناظر را نشان می‌دهند.

توزیع بولتزمن اغلب برای توصیف توزیع ذرات خرد، مانند اتم‌ها یا مولکول‌ها بر روی وضعیت‌های انرژی قابل دسترسی استفاده می‌شود. اگر سیستمی از ذرات زیادی تشکیل شده باشد، احتمال وجود یک ذره در حالت $$i$$ام عملاً برابر با این احتمال است که یک ذره تصادفی را از آن سیستم انتخاب و بررسی کنیم که در چه حالتی قرار دارد. به این ترتیب توزیع بولتزمن در حالت $$i$$ محاسبه می‌شود.

این احتمال برابر است با تعداد ذرات در حالت $$i$$ تقسیم بر تعداد کل ذرات در سیستم. این محاسبه در حقیقت کسری از ذرات است که حالت $$i$$ را اشغال می‌کنند. این احتمال توسط رابطه زیر بدست می‌آید.

$$ \large {\displaystyle p_{i} = {\dfrac {N_{i}} {N}}} $$

در رابطه بالا، $$N_i$$، تعداد ذرات در حالت $$i$$ و $$N$$ نیز تعداد کل ذرات در سیستم است. ممکن است از توزیع بولتزمن برای یافتن این احتمال استفاده کنیم. همان طور که دیده‌ایم براین اساس، احتمال برابر با کسری از تعداد ذرات است که در حالت $$i$$ هستند. پس معادله‌ای که کسر ذرات را در حالت $$i$$ نشان می‌دهد، به عنوان تابعی از انرژی آن حالت خواهد بود. به این ترتیب به رابطه زیر خواهیم رسید.

$$ \large \displaystyle {\dfrac {N_{i}}{N}} = {\frac {e^{ – {\varepsilon }_{i} /kT }}{\sum_{j = 1}^{M}{ e^{- {\varepsilon}_{j} / kT} }}} $$

این معادله برای طیف سنجی اهمیت زیادی دارد. در طیف سنجی، یک خط طیفی از اتم‌ها یا مولکول‌ها را مشاهده می‌کنیم که علاقه‌مند به رفتن از حالتی به حالت دیگر هستند. برای این که این امکان وجود داشته باشد، باید ذراتی در حالت اول وجود داشته باشند که تحت گذار قرار گیرند. ممکن است بفهمیم که این وضعیت با پیدا کردن کسر ذرات در حالت اول برآورده می‌شود.

اگر این تعداد، ناچیز باشند، انتقال به احتمال بسیار زیاد، در دمایی که محاسبه برای آن انجام شده است، مشاهده نمی‌شود. به طور کلی کسر بزرگتری از مولکول‌ها در حالت اول به معنای تعداد بیشتری از گذارها به حالت دوم است. براین اساس این خط طیفی قوی‌تر بوجود می‌آید. با این حال، عوامل دیگری نیز وجود دارند که بر شدت یک خط طیفی تأثیر می‌گذارد. برای مثال می‌توان به ممنوعیت یا مجاز بودن حالت گذر اشاره کرد.

توزیع بولتزمن مرتبط با «تابع سافت‌ماکس» (Softmax Function) یا «بیشینه-هموار» نیز هست که معمولاً در «یادگیری ماشین» (Machine Learning) استفاده می‌شود. در یکی دیگر از مطالب مجله فرادرس در مورد این تابع صحبت خواهیم کرد.

کاربرد توزیع بولتزمان در مکانیک آماری

توزیع بولتزمن در مکانیک آماری، هنگامی که با سیستم‌های ایزوله (یا تقریباً ایزوله) با ترکیب ثابت که در تعادل حرارتی (تعادل با توجه به تبادل انرژی) قرار دارند، مورد استفاده قرار می‌گیرد. کلی‌ترین حالت توزیع احتمال برای «ترکیب بُندادی» یا «آنسامبل کانونی» (Canonical Ensemble) است. البته گاهی اوقات شکل خاصی از این سیستم‌ها (مشتق‌شده از گروه کانونی) را نیز توزیع بولتزمن می‌نامند.

ترکیبات کانونی یا بندادی

ترکیبات کانونی یا آنسامبل کانونی احتمالات، برای حالت‌های مختلف یک سیستم بسته با حجم ثابت که در تعادل حرارتی هستند را محاسبه و نمایش می‌دهند. به این ترتیب ترکیبات کانونین حالت خاصی از فرم توزیع احتمال بولتمن هستند.

فراوانی‌های آماری حالت‌های زیرسیستم‌ها (در یک مجموعه غیر تعاملی)

هنگامی که سیستم مورد نظر، مجموعه‌ای از کپی‌های بسیار زیاد از یک زیر سیستم کوچکتر است، از شکل محاسبه فراوانی‌های آماری استفاده می‌شود. گاهی اوقات برای پیدا کردن مقدار احتمال در توزیع بولتزمن، فراوانی‌های آماری حالت یک زیر سیستم را مورد بررسی قرار می‌دهند.

ترکیب کانونی، زمانی که روی چنین مجموعه‌ای اعمال می‌شود، ویژگی تجزیه پذیری دارد، بنابراین تا زمانی که زیرسیستم‌های غیر تعاملی، ترکیب ثابتی داشته باشند، حالت هر زیرسیستم مستقل از بقیه است و با یک ترکیب کانونی نیز مشخص می‌شود. در نتیجه توزیع فراوانی آماری مورد انتظار برای حالت‌های زیر سیستم، به فرم توزیع بولتزمن در خواهد آمد.

آمار ماکسول–بولتزمن از گازهای کلاسیک (در یک سیستم ذرات بدون تداخل)

در سیستم‌های مبتنی بر ذره‌ها، بسیاری از ذرات، یک فضا را به اشتراک می‌گذارند و مرتباً مکان‌ها را با یکدیگر جابجا می‌کنند. فضای حالت تک ذراتی که اشغال می‌کنند، یک فضای مشترک است. آمار ماکسول–بولتزمن تعداد مورد انتظار ذرات را در یک حالت تک ذره‌ای محاسبه می‌کند که در یک گاز کلاسیک از ذرات بدون تداخل و در حالت تعادل قرار دارد. «مقدار مورد انتظار» (Expected Number) برای چنین پدیده‌ای فرم توزیع بولتزمن را دارد.

هنگامی که یک سیستم در تعادل ترمودینامیکی با توجه به هر دو تبادل انرژی و تبادل ذرات قرار دارد، شرط مربوط به به ترکیب ثابت، نادیده گرفته شد و یک «ترکیب کانونی پایه» (Grand Canonical Ensemble) به جای ترکیب کانونی اصلی به دست می‌آید. از سوی دیگر اگر هم ترکیب و هم انرژی ثابت باشند، آنگاه یک «آنسامبل میکروکانونی» (Microcanonical Ensemble) به جای آن اعمال می‌شود.

اگر زیر سیستم‌های درون یک مجموعه با یکدیگر تعامل داشته باشند، آنگاه فراوانی‌های مورد انتظار حالت‌های زیر سیستم، دیگر از یک توزیع بولتزمان پیروی نمی‌کنند و حتی ممکن است راه حل تحلیلی هم وجود نداشته باشد.

ترکیبات کانونی با این حال هنوز هم می‌تواند به صورت تجمیع اجزای کل سیستم در نظر گرفته شده و به عنوان یک کل، اعمال شوند. به این شرط که کل سیستم ایزوله شده و در تعادل حرارتی قرار گرفته باشد.

تعداد ذرات یافت شده در یک حالت تک ذره‌ای برای گازهای کوانتومی، به شرطی که در حالت تعادل بوده و در تداخل با ذرات دیگر قرار نداشته باشند، از توزیع ماکسول–بولتزمن پیروی نمی‌کنند و بیان فرم بسته و ساده‌ای برای گازهای کوانتومی در ترکیبات کانونی وجود ندارد. در ترکیبات کانونی پایه، توزیع حالت پرکننده گازهای کوانتومی با آمار و روش احتمال و «آماره فرمی–دیراک» (Fermi–Dirac statistics) یا «آماره بوز–اینشتین» (Bose–Einstein statistics)، توصیف می‌شوند. البته به این بستگی دارد که ذرات به ترتیب «فرمیون» (fermions) یا «بوزون» (bosons) باشند.

کاربرد توزیع بولتزمان در ریاضیات

در حوزه ریاضیات عمومی، توزیع بولتزمان به عنوان اندازه گیبس نیز شناخته می‌شود. در آمار و یادگیری ماشین، آن را یک «مدل لگاریتم خطی» (Log-linear Model) می‌شناسند.

یادگیری عمیق، از توزیع بولتزمن در توزیع نمونه‌ای «شبکه‌های عصبی تصادفی» (Stochastic Neural Networks) مانند «دستگاه بولتزمان» (Boltzmann’s Machine)، «دستگاه بولتزمان مقید» (Restricted Boltzmann Machine)، «مدل‌های مبتنی بر انرژی» (Energy-Based Models) و «ماشین عمیق بولتزمان» (Deep Boltzmann Machine) استفاده می‌کند.

کابرد توزیع بولتزمان در اقتصاد

توزیع بولتزمان را می‌توان برای تخصیص مجوز در تجارت و صادرات معرفی کرد. روش تخصیص جدید با استفاده از توزیع بولتزمان می‌تواند محتمل‌ترین، طبیعی‌ترین و بی‌طرفانه‌ترین توزیع مجوزهای صادرات را در بین چندین کشور توصیف کند. این توزیع، با توجه به سادگی و کاربردی بودن، روش جدید بسیاری از کسب و کارهای اقتصادی و زیست محیطی محسوب می‌شود.

توزیع بولتزمان همان شکلی را دارد که «مدل لوجیت چند جمله‌ای» (Multinomial Logit) دارد. در «مدل‌های انتخاب گسسته» (Discrete Choice Model)، ارتباط بین حداکثر سازی تصادفی و توزیع بولتزمان توسط «دانیل مک فادن» (Daniel McFadden) در اقتصاد معرفی و به کار گرفته شد.

خلاصه و جمع‌‌بندی

در این نوشتار به بررسی توزیع بولتزمان یا بولتزمن پرداختیم و بخصوص کاربرد آن در مکانیک و ترمودینامیک آماری را بیان کردیم. همانطور که گفته شد، توزیع‌های آماری، روشی برای بیان رفتار داده‌های تصادفی هستند. در این بین «لودویگ بولتزمان» با فرموله کردن رابطه بین کمیت‌های ترمودینامیکی برای وضعیت یا حالت سیستم‌ها مکانیکی، توزیع بولتزمان را معرفی کرد. همانطور که خواندید، این رابطه‌ها نیز در این نوشتار معرفی و مورد بررسی قرار گرفتند. از طرفی کاربردهای این توزیع در ریاضیات و همچنین حوزه اقتصاد در سال‌های اخیر بخصوص در بهینه‌سازی تصادفی گسسته مورد توجه است.