توزیع لاپلاس (Laplace Distribution) — به زبان ساده

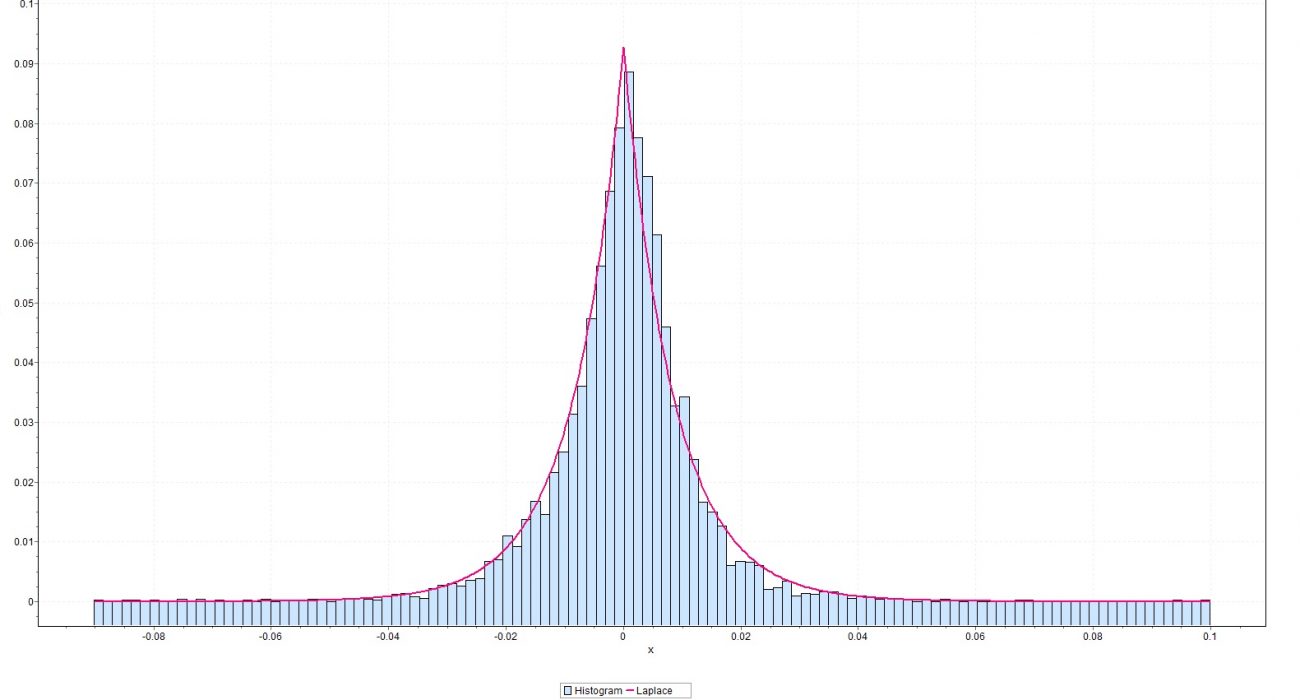
در میان توزیع‌ها و متغیرهای تصادفی پیوسته، «توزیع لاپلاس» (Laplace Distribution) دارای کاربردهای زیادی است. در این نوشتار به بررسی این توزیع می‌پردازیم و در مورد خصوصیات آن بحث خواهیم کرد. از آنجایی که این توزیع برمبنای فاصله قدرمطلق خطاها (Absolute Difference) ساخته شده است، زمانی که میانه برآوردگر بهتری نسبت به میانگین برای نقطه مرکزی داده‌ها باشد، قادر است رفتار داده‌های تصادفی را بهتر توصیف کند.

ضمناً بر حسب اینکه توزیع لاپلاس با توزیع نمایی در ارتباط است، خواندن مطلب متغیر تصادفی و توزیع نمایی — به زبان ساده ضروری به نظر می‌رسد. همچنین خواندن امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها نیز خالی از لطف نیست.

توزیع لاپلاس (Laplace Distribution)

توزیع لاپلاس را به قانون اول خطای‌های لاپلاس نسبت می‌دهند. «پیر-سیمون لاپلاس» (Pierre-Simon Laplace) دانشمند و ریاضی‌دان فرانسوی قرن ۱۸، در پی تحقیقاتی که در مورد کاهش خطای برآوردها انجام می‌داد، این توزیع آماری را بررسی کرد. او در مقاله‌ای که در سال 1774 منتشر کرد، نشان داده که فراوانی خطا‌ها را می‌توان به فرم یک تابع نمایی نشان داد. بعدها «جان کینس» (John Keynes) در سال 1901 نشان داد که توزیع لاپلاس، قدر مطلق خطا نسبت به نقطه میانه را کمینه می‌سازد.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

به این توزیع، گاهی توزیع نمایی دوتایی (Double Exponential Distribution) گفته می‌شود. زیرا می‌توان آن را به صورت دو تابع توزیع نمایی چسبیده به هم تصور کرد. نمودار تابع چگالی احتمال که در ادامه قابل مشاهده است، این موضوع را بهتر نشان می‌دهد.

تابع احتمال و توزیع تجمعی لاپلاس

اگر متغیر تصادفی $$X$$ دارای تابع چگالی احتمال $$f_X(x)$$ به صورت زیر باشد، آن یک متغیر تصادفی با توزیع لاپلاس می‌نامند. در این صورت می‌نویسند: $$X\sim Laplace(\mu,b)$$.

$$\large f(x\mid \mu ,b)={\frac {1}{2b}}\exp \left(-{\frac {|x-\mu |}{b}}\right)\,\! =\frac {1}{2b}\begin{cases}\exp \left(-{\frac {\mu -x}{b}}\right)&{\text{if }}x<\mu \\[8pt]\exp \left(-{\frac {x-\mu }{b}}\right)&{\text{if }}x\geq \mu \end{cases}$$

در این رابطه، $$\mu$$ را «پارامتر مکان» (Location Parameter) و $$b>0$$ را «پارامتر مقیاس» (Scale Parameter) می‌نامند.

نکته: اگر $$\mu=0$$ و $$b=1$$ باشد، توزیع لاپلاس از هر طرف (مجموعه مقادیر مثبت و منفی) شبیه دو توزیع نمایی با پارامتر $$\frac{1}{2}$$ و $$\frac{-1}{2}$$ است.

تابع چگالی احتمال توزیع لاپلاس بسیار شبیه توزیع نرمال است. با این حال، اگر توزیع نرمال به صورت مربع اختلاف از میانگین $$\mu$$ بیان می‌شود، در توزیع لاپلاس، تراکم یا چگالی مقادیر به واسطه تفاوت قدر مطلق مقادیر حول میانه خواهد بود. در نتيجه توزيع لاپلاس با دم‌های کشیده‌تری نسبت به توزیع نرمال رسم می‌گردد.

در تصویر زیر تابع احتمال توزیع لاپلاس برای مقدارهای مختلف پارامترهایش دیده می‌شود.

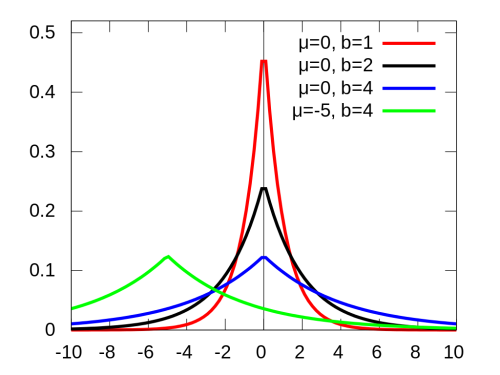
در تصویر بالا دلیل نام‌گذاری این توزیع با توزیع نمایی دوتایی به وضوح دیده می‌شود. به نظر می‌رسد که در نقطه مرکزی یا پارامتر مکان، از سمت راست یک تابع نمایی منفی و در سمت چپ نیز یک تابع نمایی نمایی منفی دیگر رسم شده است. تابع توزیع تجمعی این توزیع احتمالی نیز به صورت زیر نوشته می‌شود.

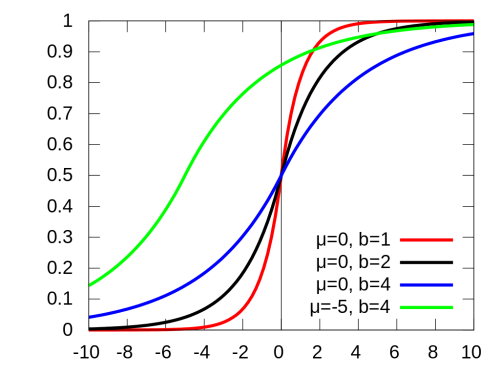
$$\large F(x) = \int_{-\infty}^x \!\!f(u)\,\mathrm{d}u = \begin{cases} \frac12 \exp \left( \frac{x-\mu}{b} \right) & \mbox{if }x < \mu \\ \large 1-\frac12 \exp \left( -\frac{x-\mu}{b} \right) & \mbox{if }x \geq \mu \end{cases}$$

به همین ترتیب می‌توان نمودار مربوط به تابع توزیع تجمعی این متغیر تصادفی را به صورت زیر ترسیم کرد.

امید ریاضی و واریانس توزیع لاپلاس

با توجه به شکل متقارن توزیع لاپلاس مشخص است که نما، میانه و میانگین در این توزیع برابر با پارامتر مکان ($$\mu$$) هستند. همچنین واریانس این متغیر تصادفی نیز $$2b^2$$ خواهد بود.

نکته: این توزیع درست به مانند توزیع نرمال، کشیدگی یا چولگی ندارد. در نمودار مربوط به تابع احتمال این توزیع، تقارن در جهت افقی و عمودی به وضوح دیده می‌شود.

برآورد پارامترهای توزیع لاپلاس

یکی از مهم‌ترین موضوعات در آمار و بخصوص توزیع‌های آماری، برآوردگرها و شیوه محاسبه برآورد برای پارامترهای توزیع‌های آماری است. در اینجا به معرفی برآوردگرهای حداکثر درستنمایی MLE یا (Maximum Likelihood Estimator) در توزیع لاپلاس می‌پردازیم. فرض کنید n مشاهده از توزیع لاپلاس به صورت $$x_{1},x_{2},...,x_{n}$$ موجود باشد. برآوردگرهای حداکثر درستنمایی برای پارامتر مکان و مقیاس به ترتیب به صورت میانه مشاهدات و میانگین قدرمطلق فاصله از میانه (AD) خواهند بود.

$$\large \widehat{\mu}=\operatorname{Median}(x_{1},x_{2},...,x_{n})$$

$$\large \widehat{b}=\operatorname{AD}(x_{1},x_{2},...,x_{n})=\frac{1}{N} \sum_{i = 1}^{n} |x_i - \hat{\mu}|$$

از آنجایی که در رابطه بالا مجموع قدر مطلق‌ها به ازاء میانه حداکثر ممکن خواهد بود، این برآوردگرها حاصل شده‌اند.

خصوصیات توزیع لاپلاس

فرض کنید که $$X$$ دارای توزیع لاپلاس با پارامترهای $$\mu$$ و $$b$$ است. در این صورت رابطه‌های زیر را خواهیم داشت.

• $$kX+c$$ نیز دارای توزیع لاپلاس با پارامترهای $$k\mu+c$$ و $$kb$$‌ است.
• اگر $$X\sim Laplace(0,b)$$ باشد، آنگاه $$|X|\sim Exp(b^{-1}$$ است.
• اگر $$X$$ و $$Y$$ مستقل با توزیع نمایی با پارامتر $$\lambda$$ باشند، آنگاه $$X-Y\sim Laplace (0,\lambda^{-1})$$ است.
• برای متغیر تصادفی $$X$$ با توزیع لاپلاس، $$|X-\mu|$$ دارای توزیع نمایی با پارامتر $$\lambda^{-1}$$ است.
• اگر $$X_1, X_2, X_3,X_4$$ دارای توزیع نرمال استاندارد باشند، آنگاه $$X_1,X_2,X_3,X_4 \sim Laplace(0,1)$$ است.
• اگر $$X$$ و $$Y$$ متغیرهای تصادفی با توزیع یکنواخت استاندارد باشند، آنگاه خواهیم داشت: $$log(\frac{X}{Y})\sim Laplace(0,1)$$ است.

شبیه‌سازی مقدارهای توزیع لاپلاس

فرض کنید متغیر تصادفی $$U\sim U(\frac{-1}{2},\frac{1}{2})$$ یعنی دارای توزیع یکنواخت پیوسته در فاصله (۱/۲و۱/۲-) باشد.

فیلم آموزش معادلات لاپلاس و پواسن در الکترومغناطیس مهندسی (رایگان) در فرادرس

کلیک کنید

آنگاه با استفاده از رابطه زیر می‌توان مقادیری از توزیع لاپلاس را تولید کرد.

$$\large X=\mu - b\,\operatorname {sgn}(U)\,\ln(1 - 2|U|)$$

در اینجا منظور از $$\operatorname {sgn}(.)$$ همان تابع علامت است. به این معنی که اگر پارامتر این تابع مثبت باشد، مقدار این تابع برابر با ۱+ و در غیراینصورت مقدار آن نیز برابر با ۱- است. یعنی داریم.

$$\large \operatorname{sgn}(x)={\begin{cases}-1&{\text{if }}x<0,\\0&{\text{if }}x=0,\\1&{\text{if }}x>0.\end{cases}}$$

کاربردهای توزیع لاپلاس

توزیع لاپلاس در تشخیص گفتار برای مدل سازی برمبنای ضریب DFT یا (Discrete Fourier transform) به کار گرفته شده است. همچنین از این توزیع برای فشرده‌سازی تصاویر به قالب JPEG نیز بهره گرفته می‌شود. ضمناً برای انجام رگرسیون خطی و برآورد پارامترهای مدل از کمینه‌سازی قدر مطلق خطای مدل نیز می‌توان بهره برد. به همین ترتیب می‌توان رگرسیون لاسو را به عنوان یک «روش رگرسیونی بیزی» (Bayesian Regression Method)  برمبنای توزیع پیشین لاپلاس در نظر گرفت.

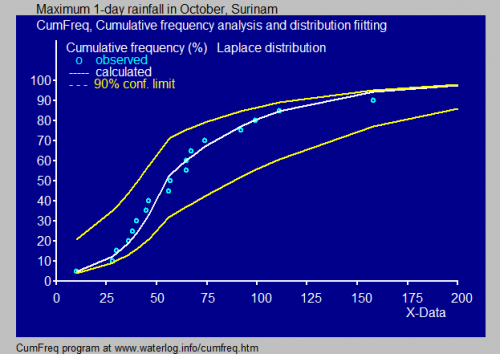
در آبخیز‌داری و علوم آب و آبشناسی، توزیع لاپلاس برای بیان پیشامدهایی با مقدارهای بسیار بزرگ (کرانگین)، به کار می‌رود. در تصویر زیر یک نمونه از برازش توزیع داده‌های مربوط به میزان حداکثر بارش در روز، بوسیله توزیع لاپلاس دیده می‌شود.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• نامساوی چبیشف – کاربرد در توزیع‌های غیرنرمال
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^