جدول توزیع نرمال استاندارد – به زبان ساده
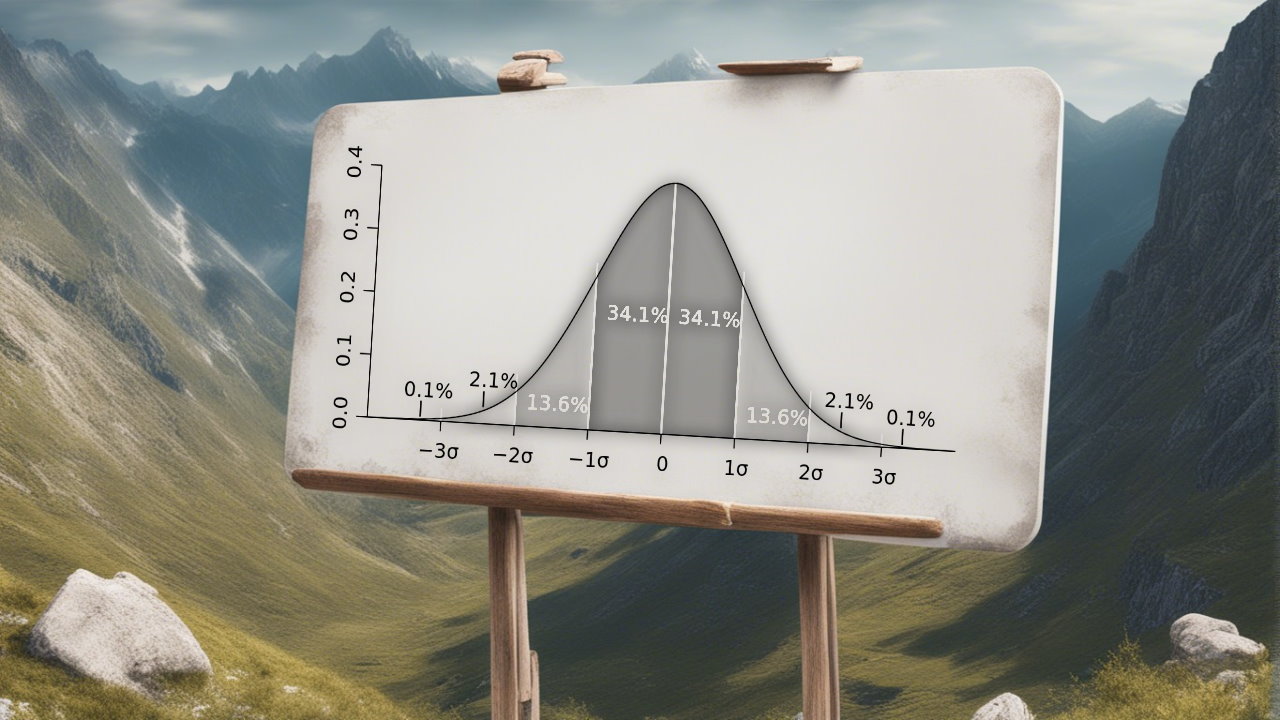
در این نوشته قصد داریم شما را با جدول توزیع نرمال استاندارد آشنا کنیم. این جدول در بسیاری از محاسبات آماری کاربرد دارد.
در نمودار تعاملپذیر فوق منحنی «زنگوله ای شکل» توزیع نرمال استاندارد را میبینید. توزیع نرمال استاندارد، یک توزیع نرمال با میانگین 0 و انحراف معیار 1 است. این نمودار، درصد جمعیت را در بازههای مختلف به شما نشان می دهد:
- بین 0 و Z
- کمتر از Z
- بیشتر از Z
دقت نمودار فوق تا %0.1 است، برای مثال %17.36 به %17.4 گرد میشود.
همچنین برای مشاهده درصدهای مربوط به جدول توزیع نرمال استاندارد، میتوانید از حدول زیر نیز استفاده نمایید.

استفاده از نرمافزارهای آماری بخصوص SPSS، اجرای محاسبات آماری را سادهتر کرده و موجب دقت بیشتر در فرمولهای محاسباتی و کسب نتایج دقیقتر میشود. در آموزشی که در ادامه لینک آن آورده شده، به کمک نرمافزار SPSS بسیاری از محاسبات و نمودارهای آماری معرفی و نحوه ایجاد آنها در این نرمافزار بازگو شده است.
جدول
میتوانید اعداد دقیقتری را با استفاده از جدول زیر بدست آورید.
جدول مساحت زیر نمودار را از 0 تا Z نشان میدهد. به جای یک جدول بلند، ما مقادیر یک دهمها (0.1) را به صورت ستونی و مقادیر یکصدمها (0.01) را به صورت ردیفی نوشتهایم. (مثال استفاده از جدول، در ادامه آمده است.)

مثال: درصد جمعیت بین 0 و 0.45
از ردیف 0.4 شروع کنید و تا 0.45 پیش بروید، مقدار نوشته شده در این نقطه 0.1736 است و 0.1736 برابر است با %17.36. پس %17.36 از جمعیت بین 0 و 0.45 انحراف از میانگین است.
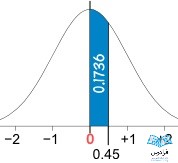
از آنجایی که منحنی متقارن است، همین جدول میتواند برای مقادیری که در جهت عکس هستند نیز استفاده شود. پس عدد منفی 0.45 نیز مساحتی برابر با 0.1736 دارد.
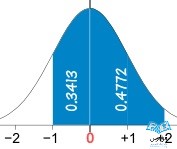
مثال: درصد جمعیت Z بین 1- و 2
پاسخ: از 1- تا 0 همانند 0 تا 1+ است، بنابراین در ردیف 1.0، ستون اول یا 1.00، مقدار 0.3413 ثبت شده است.
برای محاسبه از 0 تا 2+، در ردیف 2.0، ستون اول یا 2.00، مقدار 0.4772 ثبت شده است. بنابراین دو مقدار فوق را جمع میکنیم تا مجموع بین 1- تا 2را بدست بیاوریم:
0.3413 + 0.4772 = 0.8185
و 0.8185 نیز برابر %81.85 است.
پس %81.85 از جمعیت بین 1- و 2+ انحراف از میانگین قرار دارند.
بدین ترتیب می توانید به راحتی با استفاده از نمودار و جدول فوق محاسبات آماری مربوط به توزیع نرمال خود را انجام دهید.
مجموعهای از آموزشهای فرادرس به مباحث آمار و اجرای آنها در نرمافزار SPSS اختصاص دارد. یکی از فیلمهای مربوط به این مجموعه، به نام آموزش نرمافزار آماری SPSS، به معرفی نحوه ورود دادهها از پرسشنامه به این نرمافزار پرداخته و بعضی از شاخصها و نمودارهای آماری را به منظور تحلیل پرسشنامه مورد بررسی قرار داده است. محاسبات ساده آمارهای توصیفی مانند میانگین، میانه، نما، واریانس، ضریب تغییرات، ضریب چولگی، برجستگی یا کشیدگی در این آموزش مورد اشاره قرار گرفته است. همچنین در بخشی دیگری از این آموزش، نحوه رسم نمودارهای آماری و قالب بندی خروجی آموزش داده شده است.
این فیلم آموزشی با طول مدت زمان ۷ ساعت و ۵۳ دقیقه، به مباحثی پرداخته است که در ادامه، فهرستوار به آنها اشاره خواهیم کرد.
- آشنایی با رابط کاربری نرمافزار و انواع پنجرههای آن
- معرفی انواع متغیر و مقیاسهای اندازهگیری
- معرفی شاخصهای جمعیت (تمرکز و پراکندگی)
- ورود دادههای و انجام محاسبات روی آنها (ایجاد متغیرهای جدید به کمک محاسبه یا طبقهبندی کردن متغیرهای کمی)
- استخراج آمارههای توصیفی مانند میانگین و انحراف معیار و شاخصهای تقارن
- آشنایی با مفهوم جداول توافقی (Crosstab) و ایجاد آنها
- رسم نمودارهای آماری (نمودار ستونی، میلهای و نمودار فراوانی)
- تنظیم و قالببندی خروجی نرم افزار در پنجره SPSS Output
این آموزش به کسانی که در حوزه آمار و پردازش اطلاعات با نرمافزارهای محاسبات آماری، بخصوص SPSS، فعالیت دارند، پیشنهاد میشود. پیشنیاز برای فیلم آموزشی مذکور، آگاهی با نحوه محاسبات آماری و فرمولهای مربوط به آمار توصیفی است. به این ترتیب، بیشترین استفاده را از آن خواهید برد.










p value چیه بچه ها فردا امتحان دارم
باسلام و خسته نباشید.
ببخشید اگر در استاندارد سازی Zکوچکتر از 4.5 بشه مقدار را چجوری باید بدست آورد؟
آخه در جدول نرمال تا 3.9 بیشتر وجود نداره….
ممنون میشم جواب بدید.
سلام .زمانی که u در توزیع نرمال منفی میشود چگونه ان را حل کنیم ؟
و زمانی که بازه ما بین مثلا [0،5]است و میانگین ما هم صفر است چگونه توزیع نرمال برای ان محاسبه میشود
سلام
یک سوال بی ارتباط با این مبحث دارم
ممنون میشم پاسخ بدید؛ در توزیع نرمال استاندارد، وقتی سطح اطمینان ۹۵ درصد باشد، z برابر ۱.۹۶ است
این ۱.۹۶ ماهیتا چیست و چه تفسیری دارد؟
جایی دیده بودم که به آن ضریب اطمینان گفته میشود؛ اما تفسیر ضریب اطمینان چیست؟
سلام استاد
در سوال قبلی چرا به جای ۰/۹۵مقدار۰/۴۵ را محاسبه کردید؟
با سلام و وقت به خیر خدمت همراه مجله فرادرس
پاسخ به سوال شما در سوال قبلی گفته شده است.
(البته در جدول مربوط به مقاله گفته شده، فقط مقدار احتمال برای ناحیه بالایی توزیع نرمال آورده شده است از آنجایی که مجموع احتمال برای قسمت چپ منحنی نرمال برابر با ۰.۵ است پس باید به دنبال مقدار ۰.۴۵ بگیردیم.)
به همین علت از روی جدول مقدار نقطه با احتمال 0.45 را پیدا کرده و آن را ملاک قرار میدهیم.
از این که با دقت مطالب مجله فرادرس را مطالعه میکنید بسیار سپاسگزاریم!
سلام.
من برای درس طراحی آزمایشها به این جدول نیاز دارم. ولی من z رو ندارم که آلفا رو پیدا کنم؟
میخوام از روی آلفا z پیدا کنم ؟
چطور میتونم
سلام و سپاس از توجه شما به مطالب فرادرس؛
برای مشخص کردن مقدار z برحسب آلفا کافی است که مقدار آلفای (احتمال یا مقدار تابع توزیع تجمعی) را در داخلی جدول پیدا کنید. آنگاه مقدار سطر و ستون سلول مورد نظر در جدول، مقدار z را تعیین میکند. برای مثال فرض کنید که قرار است مقدار z را برای احتمال a=0.95 پیدا کنید. در داخل جدول به دنبال مقدار 0.95 میگردیم. (البته در جدول مربوط به مقاله گفته شده، فقط مقدار احتمال برای ناحیه بالایی توزیع نرمال آورده شده است از آنجایی که مجموع احتمال برای قسمت چپ منحنی نرمال برابر با 0.5 است پس باید به دنبال مقدار 0.45 بگیردیم. مقدار 0.4495 به مقدار مورد نظر ما بسیار نزدیک است. از آنجایی سطر این سلول برابر با 1.6 و ستون آن مقدار 0.04 است، مقدار z=1.64 خواهد بود.
برای آشنایی بیشتر با این موضوع میتوانید نوشتار محاسبه توزیع نرمال در اکسل را مطالعه کنید.
باز هم از اینکه همراه فرادرس هستید بسیار خوشحالیم.
موفق و پاینده باشید.
با سلام
لطفا در وبلگ در مورد توزیع وایبول و کاربرد آن توضیحی ارایه بدهید.
با تشکر
با سلام
مقدار (0.17)∅ رو چطور میتونیم حساب کنیم؟ فی کوچکه یعنی تجمعی نیست
سپاس
با تشکر از راهنمایی استاد محترم دکتر ری بد در واقع سوال کامل تر من این هست: اگر داشته باشیم : P(5×1 + 8×2 + 10×3 = 0.9 ( یعنی اگر احتمال رخ دادن محدودیت 90 درصد باشد) و b دارای توزیع نرمال باشدیعنی b => N( μ = 100 , σ^2 = 100 ) با این فرض ها عبارت زیر چه معنایی دارد؟ P[(5×1 + 8×2 + 10×3 – 100) / 10 = 0.9 = Φ(1.285)
نوشته من رو ناقص نوشتین با تشکر کاملش اینه با تشکر از راهنمایی استاد محترم دکتر ری بد در واقع سوال کامل تر من این هست اگر داشته باشیم P(5×1 + 8×2 + 10×3 ≤ b ) ≥ 0.9 ( یعنی اگر احتمال رخ دادن محدودیت 90 درصد باشد) دارای توزیع نرمال باشد یعنیbو b => N( μ = 100 , σ^2 = 100 ) با این فرض ها عبارت زیر چه معنایی دارد؟ P [(5×1 + 8×2 + 10×3 – 100) / 10 ≤ (b-100) / 10] ≥ 0.9 = Φ(1.285)
رابطهای که شما نوشتهاید به معنی مقدار تابع توزیع نرمال استاندارد در نقطه 1.285 است. یعنی اگر Z یک متغیر تصادفی با توزیع نرمال استاندارد باشد P(Z<1.285) باشد برابر با عبارت مورد نظر شما خواهد بود… که در جدول تقریبا برابر با 0.3397 است از انجایی که این جدول فقط مقدار احتمال را برای مقدارهای بزرگتر از ۰ ثبت کرده کافی است با توجه به متقارن بودن توزیع نرمال استاندارد مقدار 0.5 را هم به 0.3397 اضافه کنیم تا پاسخ شما کامل شود. 0.3397+0.5=0.8397
با سلام و تشکر از مطالب آموزنده شما این عبارت به چه معناست ؟ Φ(1.285)