اعداد باینری علامت‌دار – به زبان ساده

پیش از شروع لازم به ذکر است که قسمت‌های اول، دوم، سوم، چهارم و پنجم این مطلب را می‌توانید از طریق کلیک کردن روی لینک مرتبط به هر بخش مطالعه کنید؛ در ریاضیات اعداد مثبت که شامل صفر نیز می‌شوند به‌صورت اعداد بی علامت نمایش داده می‌شوند. یعنی برای اینکه نشان بدهیم این اعداد مثبت هستند، علامت + در برابر آن‌ها قرار نمی‌دهیم.

با این حال وقتی با اعداد منفی سروکار داریم، یک علامت (-) در مقابل آن‌ها قرار می‌دهیم تا نشان دهیم که این عدد مقدار منفی دارد و از عدد بی علامت مثبت متفاوت است. اعداد باینری علامت‌دار نیز همینطور هستند.

در مدارهای دیجیتال هیچ تدارکی برای قرار دادن یک علامت بعلاوه یا منها در کنار عدد دیده نشده است. چون سیستم‌های دیجیتال با اعداد باینری کار می‌کنند که به‌صورت صفر و یک نمایش داده می‌شوند. زمانی که این «1» و «0» ها در مدارهای میکروالکترونیک کنار هم قرار می‌گیرند، بیت (bit) نامیده می‌شوند (که از عبارت BInary digiT اخذ شده است). این اعداد در چند واحد قرار می‌گیرند که به نام‌هایی مانند بایت (8 بیت) یا کلمه (word = دو بایت) نامیده شده‌اند.

یک عدد باینری هشت بیتی (یک بایت) می‌تواند مقداری بین 0 (00000000₂) تا 255 (11111111₂) داشته باشد یعنی 2⁸=256 ترکیب مختلف از بیت‌ها، یک بایت ۸ بیتی منفرد را تشکیل می‌دهند. بنابراین یک عدد باینری بی علامت مانند 010011012 برابر با مقدار ده‌دهی 64 + 8 + 4 + 1 = 77₁₀ خواهد بود. اما سیستم‌های دیجیتال و رایانه‌ها باید توانایی استفاده و تغییر اعداد منفی را نیز مانند اعداد مثبت داشته باشند.

نمادگذاری «علامت-بزرگی»

اعداد ریاضی به طور کلی از یک علامت و یک مقدار (بزرگی) تشکیل یافته‌اند که علامت، نشان می‌دهد عدد مثبت یا منفی است و مقدار نیز بزرگی عدد را نشان می‌دهد. برای مثال 23، 156+ یا 274-. نمایش اعداد به این‌ روش به‌صورت نمایش «علامت-بزرگی» نامیده می‌شود، زیرا بیتی که در سمت چپ قرار دارد علامت عدد را نشان می‌دهد و باقی ارقام بزرگی این عدد را نشان می‌دهند.

فیلم آموزش اعداد علامت دار در برنامه نویسی اسمبلی (رایگان) در فرادرس

کلیک کنید

نمادگذاری «علامت-بزرگی» ساده‌ترین و یکی از رایج‌ترین روش‌های نمایش اعداد مثبت و منفی در دو طرف صفر است. بنابراین برای اعداد منفی، به سادگی با تغییر علامت، عدد مثبت متناظر به دست می‌آیند. بدین ترتیب هر عدد مثبت یک عدد متناظر با علامت منفی برای خود دارد برای مثال 2+ و 2+، 10+ و 10- و غیره.

اما وقتی تنها یک تعداد صفر و یک داریم، چگونه می‌توانیم اعداد باینری علامت‌دار را نمایش بدهیم. می‌دانیم که ارقام باینری تنها دو حالت دارند یعنی 1 یا 0 هستند. از طرف دیگر یک علامت هم دو حالت دارد، یعنی «+» یا «-» است.

در این صورت می‌بینیم که در نمادگذاری «علامت-بزرگی» (SM)، مقادیر مثبت و منفی با تقسیم کردن n بیت به دو قسمت تقسیم می‌شوند: یک بیت برای علامت و n-1 بیت برای مقدار که یک عدد باینری خالص است. برای مثال عدد ۵۳ را می‌توان به‌صورت یک عدد باینری علامت‌دار ۸ بیتی همانند زیر نمایش داد.

اعداد باینری علامت‌دار مثبت

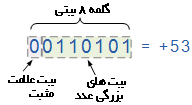
اعداد باینری علامت‌دار منفی

مشکل این نحوه نمایش این است که ما قبلاً یک محدوده کامل از اعداد باینری بدون علامت n بیتی داشتیم، اما اینک یک عدد باینری علامت‌دار n-1 بیتی داریم که محدوده ارقام آن کاهش یافته است.

-(2^(n-1))    +(2^(n-1))

بنابراین برای مثال اگر چهار بیت برای نمایش یک عدد باینری علامت‌دار داشته باشیم (یک بیت برای علامت و 3 بیت برای نشان دادن بزرگی عدد) در این محدوده، اعداد واقعی که می‌توانیم در روش «علامت-بزرگی» نشان دهیم به‌صورت زیر خواهد بود:

-(2^(4-1)-1)   →   +(2^(4-1)-1)

-(2⁽³⁾-1)    →   +(2⁽³⁾-1)

7+   →    7-

در حالی که قبلاً محدوده اعداد باینری ۴ بیتی بدون علامت از ۰ تا ۱۵ یا در نمایش مبنای ۱۶ (هگزادسیمال) از 0 تا F بودند، اما در این‌ روش، نمایش به محدوده اعداد 7- تا 7+ کاهش یافته است. بنابراین عدد باینری بدون علامت، بیت منفرد علامت را ندارد و می‌تواند محدوده باینری بزرگ‌تری داشته باشد، چون معنی‌دارترین بیت (MSB، یعنی بیت سمت چپ) تنها نشان دهنده یک رقم است و به عنوان بیت علامت استفاده نمی‌شود.

0 مثبت است یا منفی؟

عیب دیگر نحوه نمایش «علامت-بزرگی» اعداد باینری این است که می‌توان هم یک نمایش مثبت برای عدد صفر داشت (0+) یا 0000₂ و هم یک صفر منفی، 0- یا 1000₂ که هر دو معتبر هستند ولی هیچ کدام صحیح نیستند.

فیلم آموزش گیت های منطقی (رایگان) در فرادرس

کلیک کنید

در مثال زیر برای اعداد باینری علامت‌دار، مقادیر ده‌دهی را با استفاده از فرمت «علامت-بزرگی» به اعداد باینری علامت‌دار تبدیل می کنیم.

توجه داشته باشید که در همه اعداد باینری 4 بیت، 6 بیت، 8 بیت، 16 بیت یا 32 بیت، همه بیت‌ها باید مقداری داشته باشند، از این‌رو از 0 برای پر کردن فاصله بین بیت علامت که در سمت چپ قرار می‌گیرد و نخستین بیت با بالاترین مقدار 1 استفاده می‌شود.

نمایش «علامت-بزرگی» یک عدد باینری، روش ساده‌ای برای استفاده و درک اعداد باینری علامت‌دار است، چون ما از این سیستم به طور روزمره برای اعداد معمولی ده‌دهی (بر مبنای 10) در محاسبات ریاضی استفاده می‌کنیم. کافی است وقتی عدد باینری منفی است، یک (1) و وقتی مثبت است یک (0) به ابتدای آن اضافه کنیم.

با این حال استفاده از این روش «علامت-بزرگی» ممکن است به این حالت منتهی شود که دو الگوی بیتی مختلف، مقدار باینری یکسانی داشته باشند. برای مثال 0+ و 0- به ترتیب به‌صورت 0000 و 1000 به عنوان یک عدد باینری 4 بیتی نمایش می‌یابند. بنابراین می‌بینیم که در این روش برای عدد صفر ممکن است دو نمایش داشته باشیم، یعنی یک صفر مثبت (0000₂) و صفر منفی (1000₂) که موجب پیچیدگی‌های زیادی در سیستم‌های محاسباتی و دیجیتالی می‌شود.

«مکمل 1» یک عدد باینری علامت‌دار

مکمل یک (یا آن طور که غالباً استفاده می‌شود «مکمل 1») روش دیگری برای نمایش اعداد باینری منفی در یک سیستم اعداد باینری علامت‌دار است. در روش «مکمل 1» اعداد مثبت (به نام غیر مکمل نامیده می‌شوند) همانند روش قبلی بزرگی-علامت بدون تغییر باقی می‌مانند. اما اعداد منفی با انتخاب «مکمل 1» (معکوس سازی) عدد باینری مثبت ایجاد می‌شوند. از آنجا که اعداد مثبت همیشه با 0 آغازمی شوند، عدد مکمل همیشه با 1 آغاز می‌شود که نشان‌دهنده یک عدد منفی است.

فیلم آموزش مدار منطقی – مرور و حل مساله در فرادرس

کلیک کنید

«مکمل 1» یک عدد باینری منفی، معادل «مکمل 1» همتای مثبت آن است. بنابراین برای داشتن «مکمل 1» برای یک عدد باینری کافی است به ترتیب هر بیت را که 0 است به 1 و هر بیت را که 1 است به 0 تغییر دهیم. بدین ترتیب «مکمل 1» عدد 10010100₂ به‌سادگی عدد 01101011₂ است چون همه ارقام 1 به 0 تبدیل شده‌اند و برعکس.

آسان‌ترین روش برای یافتن «مکمل 1» یک عدد باینری علامت‌دار، در زمان ساخت مدارهای محاسبات باینری یا دیکودر منطقی، استفاده از اینورترها است. اینورتر یک تولیدکننده مکمل طبیعی است و می‌تواند به‌موازات اجزای دیگر برای محاسبه «مکمل 1» هر عدد باینری به‌صورت زیر مورد استفاده قرار گیرد.

«مکمل 1» با استفاده از اینورتر

در این صورت می‌بینیم که یافتن «مکمل 1» یک عدد باینری N آسان است، چون کافی است صرفاً بیت‌های 1 را 0 کنیم و بیت‌های 0 را به 1 تبدیل کنیم تا به عدد معادل N- برسیم. همچنین همانند روش نمایش قبلی «بزرگی-علامت» روش «مکمل 1» نیز می‌تواند یک نمادگذاری بیتی برای نمایش اعداد به‌صورت ^(n-1)2- و 1-^(n-1)2+ داشته باشد. برای مثال یک نمایش 4 بیتی در قالب «مکمل 1» را می‌توان برای نمایش اعداد در محدوده‌ای از 7- تا 7+ داشت که همانند روش قبل دو نمایش برای صفر، به‌ صورت 0000 (0+) و 1111 (0-) خواهیم داشت.

جمع و تفریق با استفاده از «مکمل 1»

یکی از مزایای روش «مکمل 1»، در زمان جمع و تفریق دو عدد باینری قابل مشاهده است. در ریاضیات، تفریق می‌تواند به روش‌های مختلفی انجام گیرد. مثلاً A-B همان A+(-B) یا B+A- است. از این‌رو پیچیدگی تفریق دو عدد را با تبدیل کردن آن به جمع دو عدد می‌توان از میان برداشت.

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

می‌دانیم که هنگام جمع باینری از همان قواعد جمع معمولی استفاده می‌کنیم، به‌جز این‌که در حالت باینری تنها دو بیت (رقم) وجود دارند و بزرگ‌ترین رقم، «1» است (مانند «9» که بزرگ‌ترین رقم در سیستم ده‌دهی است) و از این‌رو ترکیب احتمالی جمع باینری به‌صورت زیر است:

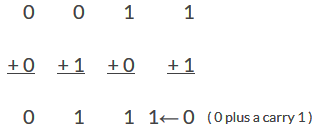
وقتی هر دو عددی که می‌خواهیم جمع کنیم مثبت باشند (مجموع A+B) می‌توان آن‌ها را با استفاده از جمع مستقیم (شامل عدد و بیت علامت) به هم اضافه کرد. چون وقتی بیت‌های منفرد به هم اضافه می‌شوند «0+0»، «0+1» یا «1+0» نتیجه جمع یا «0» است و یا «1». این امر به این دلیل است که وقتی دو بیت متفاوت به هم اضافه شوند (0+1 یا 1+0) نتیجه 1 خواهد بود. به طور مشابه وقتی دو بیت که به هم اضافه می‌شوند، مشابه باشند (0+0 یا 1+1) نتیجه 0 خواهد بود. تا این‌که به جمع 1+1 برسیم که نتیجه یک 0 و یک 1 اضافی خواهد بود. در ادامه در این مورد بیشتر توضیح داده‌ایم.

تفریق دو عدد باینری

در یک سیستم دیجیتال 8 بیتی می‌خواهیم دو عدد 115 و 27 را با استفاده از روش «مکمل 1» از هم کم کنیم. در سیستم ده‌دهی این تفریق به‌صورت زیر است: 88 = 27-115.

فیلم آموزش اعداد علامت دار در برنامه نویسی اسمبلی (رایگان) در فرادرس

کلیک کنید

ابتدا باید اعداد ده‌دهی را به سیستم باینری تبدیل کنیم و با افزودن 0 به اول اعداد مطمئن شویم که هر عدد بیت‌های یکسانی دارد و آن‌ها را به اعداد 8 بیتی (بایت) تبدیل کنیم. بنابراین:

01110011₂ باینری = 115₁₀

00011011₂ باینری = 27₁₀

اینک می‌توانیم مکمل عدد باینری دوم (00011011) را بیابیم، در حالی که عدد اول (01110011) را بدون تغییر حفظ می‌کنیم. بنابراین با تغییر دادن همه 1 ها به 0 و همه 0 ها به 1، «مکمل 1» عدد باینری 00011011 برابر با 11100100 خواهد بود.

افزودن عدد اول به مکمل عدد دوم به‌صورت زیر خواهد بود:

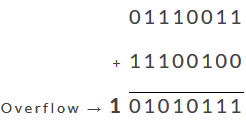
بیت overflow

از آنجایی که سیستم دیجیتال باید با 8 بیت کار کند، تنها 8 رقم نخست برای ارائه پاسخ مجموع کافی خواهد بود و بیت آخر (بیت 9) را نادیده می‌گیریم. این بیت به نام بیت اورفلو (overflow) نامیده می‌شود. اورفلو زمانی رخ می‌دهد که مجموع ستون سمت چپ یک رقم اضافی تولید کند. این بیت اضافی اورفلو را می‌توان به طور کامل نادیده گرفت یا برای محاسبات به قطعه دیجیتال بعدی ارسال کرد. اورفلو نشان می‌دهد که پاسخ مثبت است. اگر اورفلو وجود نداشته باشد در این صورت عدد منفی است.

فیلم آموزش گیت های منطقی (رایگان) در فرادرس

کلیک کنید

نتیجه 8 بیت حاصل از محاسبات فوق عدد 01010111 است (اورفلو 1 حذف شد) و برای این‌که آن را از حالت «مکمل 1» به یک عدد واقعی تبدیل کنیم باید عدد 1 را به نتیجه «مکمل 1» اضافه کنیم. بنابراین:

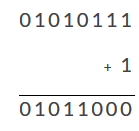
بنابراین تفریق 27 (00011011₂) از 115 (01110011₂) با استفاده از روش «مکمل 1» در سیستم باینری نتیجه‌ای برابر با 01011000₂ یا (64 + 16 + 8) = 88₁₀ در سیستم ده‌دهی خواهد داد.

در این صورت می‌بینیم که اعداد باینری علامت‌دار یا بی علامت را می‌توان با استفاده از روش «مکمل 1» و فرایند جمع زدن، از هم کسر کرد. می‌توان از آدرس باینری مانند TTL 74LS83 یا 74LS283 برای افزودن یا کم کردن دو عدد علامت‌دار 4 بیتی یا الحاق به هم برای تولید آدرس 8 بیتی کامل استفاده کرد.

«مکمل دو» یک عدد باینری علامت‌دار

مکمل دو (یا آن طور که معمولاً نوشته می‌شود: «مکمل 2») روش دیگری مشابه روش «بزرگی-علامت» و روش «مکمل 1» است که می‌توان برای نمایش اعداد باینری منفی در سیستم اعداد باینری علامت‌دار مورد استفاده قرار داد. در روش «مکمل 2» اعداد مثبت دقیقاً همانند روش قبل، مثل اعداد باینری بی علامت هستند. اما اعداد منفی به‌صورت یک عدد باینری نمایش می‌یابند که وقتی به معادل مثبت خود اضافه شوند، نتیجه 0 خواهد بود.

در روش «مکمل 2»، یک عدد منفی، «مکمل 2» عدد مثبت متناظر خود است و کسر کردن دو عدد از هم به‌صورت («مکمل 2» B)+ A–B = A با فرایندی مشابه روش قبل خواهد بود. «مکمل 2» همان «مکمل 1» + 1 است.

مزیت اصلی روش «مکمل 2» نسبت به «مکمل 1» این است که مشکل وجود 0 مضاعف وجود ندارد و تولید یک «مکمل 2» از عدد باینری بسیار آسان‌تر است. بنابراین اجرای عملیات‌های محاسباتی زمانی که اعداد به روش «مکمل 2» نمایش می‌یابند، راحت‌تر است.

مزیت روش «مکمل 2»

به تفریق دو عدد 8 بیتی 115 و 27 مثال فوق با استفاده از روش «مکمل 2» توجه کنید. از مثال فوق به خاطر داریم که معادل‌های باینری به‌صورت زیر هستند:

01110011₂ باینری = 115₁₀

00011011₂ باینری = 27₁₀

این اعداد 8 بیتی هستند و بنابراین 2⁸ رقم برای نمایش مقادیر وجود دارند که در باینری معادل عدد 100000000₂ یا 256₁₀ است. در این صورت «مکمل 2» عدد 27₁₀ به‌صورت زیر است:

(2⁸)₂-00011011 = 100000000 – 00011011 = 11100101₂

ساختن مکمل عدد دوم آن را منفی می‌کند و بنابراین تفریق آن از عدد اول بسیار ساده‌تر می‌شود و کافی است آن‌ها را با هم جمع کنیم یعنی 115 + («مکمل 2» عدد دوم) به‌صورت زیر:

01110011 + 11100101 = 1 01011000₂

همانند مثال قبل بیت 9 اضافی حذف می‌شود چون ما فقط به 8 بیت اول نیاز داریم بنابراین همانند مثال قبل به عدد زیر می‌رسیم: 01011000₂ یا (64 + 16 + 8) = 88₁₀

خلاصه اعداد باینری علامت‌دار

دیدیم که اعداد باینری منفی را می‌توان با استفاده از بیت منتهی‌الیه سمت چپ به عنوان بیت علامت نمایش داد. اگر یک عدد باینری n بیتی علامت‌دار باشد، در این صورت با اختصاص اولین بیت به علامت عدد، n-1 بیت برای نمایش عدد باقی می‌ماند.

فیلم آموزش مدار منطقی – مرور و حل مساله در فرادرس

کلیک کنید

برای مثال در یک عدد باینری 4 بیتی تنها 3 بیت برای نمایش عدد وجود دارد. با این حال اگر عدد باینری بی علامت باشد، می‌توان از همه بیت‌ها برای نمایش عدد استفاده کرد.

نمایش عدد باینری علامت‌دار به طور معمول به‌صورت نمادگذاری «علامت-بزرگی» نامیده می‌شود و اگر بیت علامت 0 باشد عدد مثبت است. در صورتی که بیت علامت برابر با 1 باشد، عدد منفی است. زمانی که عملیات‌های محاسباتی بر روی اعداد باینری علامت‌دار انجام می‌دهیم، بسیار راحت‌تر است که از مکمل اعداد برای اعداد منفی استفاده کنیم. ایجاد مکمل یک روش جایگزین برای نمایش اعداد باینری منفی است. این سیستم کدینگ جایگزین، امکان تفریق اعداد با استفاده از عملیات جمع ساده را فراهم می‌کند.

از آنجا که اعداد مثبت در سیستم «علامت-بزرگی» همواره با 0 شروع می‌شوند مکمل آن‌ها نیز همواره با 1 آغاز می‌شود که نشان دهنده عدد منفی است. در جدول زیر این مطالب به طور خلاصه مورد اشاره قرار گرفته است.

مقایسه عدد باینری علامت‌دار 4 بیتی

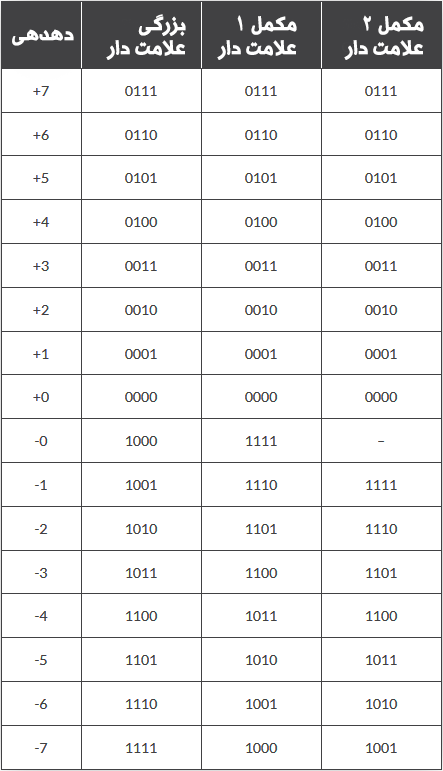
روش‌های مکمل علامتی برای اعداد باینری به‌صورت «مکمل 1» یا «مکمل 2» هستند. «مکمل 1» و «مکمل 2» برای یک عدد باینری، مهم هستند، زیرا امکان نمایش اعداد منفی را ایجاد می‌کنند. روش «مکمل 2» در محاسبات رایانه‌ای به طور معمول برای مدیریت اعداد منفی مورد استفاده قرار می‌گیرد و تنها عیبی که دارد این است که اگر بخواهیم اعداد باینری منفی را در سیستم اعداد باینری علامت‌دار نمایش بدهیم، باید بخشی از محدوده اعداد مثبتی که قبلاً داشتیم را از دست بدهیم.

فیلم مجموعه آموزش طراحی مدار الکتریکی و تحلیل – مقدماتی تا پیشرفته در فرادرس

کلیک کنید