۵ روش بصری سازی سریع و ساده در پایتون — راهنمای کاربردی

یکی از عمده‌ترین وظایف مشاغل دانشمند داده، «بصری‌سازی داده‌ها» (Data Visualization) است. در مراحل اولیه یک پروژه غالباً یک «تحلیل اکتشافی داده‌ها» (Exploratory Data Analysis) یا به اختصار EDA اجرا می‌شود تا بینش‌هایی در خصوص داده‌ها به دست آید. ایجاد بصری‌سازی به ما کمک می‌کند که موارد مختلف را به خصوص در مورد مجموعه داده‌های با ابعاد بالا، روشن‌تر و ساده‌تر درک کنیم. در مراحل پایانی پروژه نیز ارائه نتیجه نتایج به روشی روشن، منسجم و جامع به مخاطبان که غالباً افراد غیر فنی هستند تا بتوانند آن را درک کنند، از اهمیت بالایی برخوردار است. در این مقاله قصد داریم 5 روش بصری‌سازی سریع و ساده در پایتون را مورد بررسی قرار دهیم و تابع‌های ساده و سریعی با استفاده از کتابخانه Matplotlib پایتون بنویسیم.

Matplotlib یک کتابخانه محبوب پایتون است که می‌توان از آن برای ایجاد بصری‌سازی داده‌ها به روشی کاملاً آسان بهره گرفت. با این حال تنظیم داده‌ها، پارامترها، شکل‌ها و رسم نمودارها به صورت تکراری در همه پروژه‌ها کاری کاملاً وقت‌گیر و ملال‌آور محسوب می‌شود. در ادامه، نموداری را می‌بینید که امکان گزینش روش مناسب بصری‌سازی را به شما می‌دهد.

نمودارهای پراکندگی

«نمودارهای پراکندگی» (Scatter Plots) برای نمایش رابطه بین دو متغیر عالی هستند، زیرا امکان دیدن مستقیم توزیع همه داده‌ها را فراهم می‌سازند. همچنین می‌توانید رابطه بین گروه‌های مختلف داده‌ها را صرفاً از طریق کدگذاری رنگی چنان که در تصویر زیر دیده می‌شود، مشاهده کنید. اگر می‌خواهید رابطه بین سه متغیر را بصری‌سازی کنید هم مشکلی وجود ندارد، کافی است از پارامترهای دیگری مانند اندازه نقطه برای کدگذاری سه متغیر مانند کاری که در تصویر دوم زیر انجام داده‌ایم بهره بگیرید. همه این نقاط که صحبت کردیم، در نمودار نخست نیز قابل نمایش هستند.

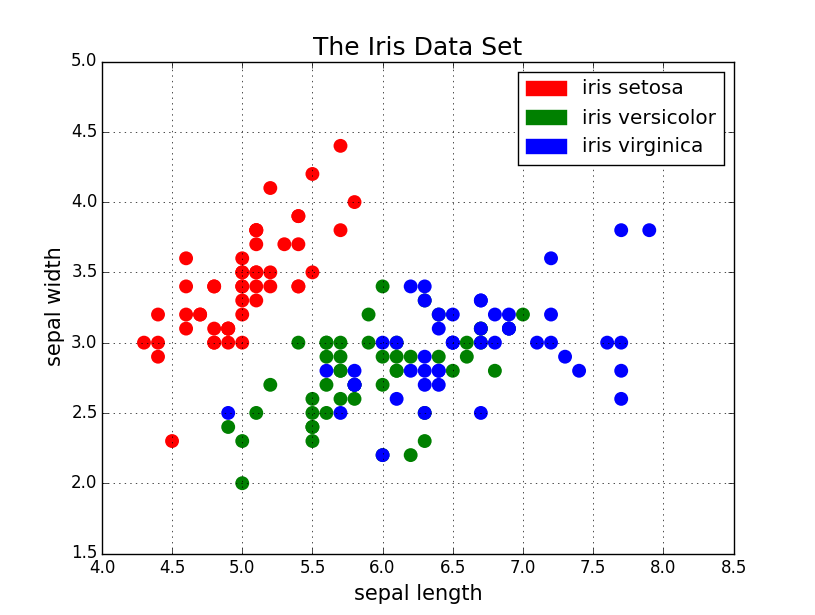
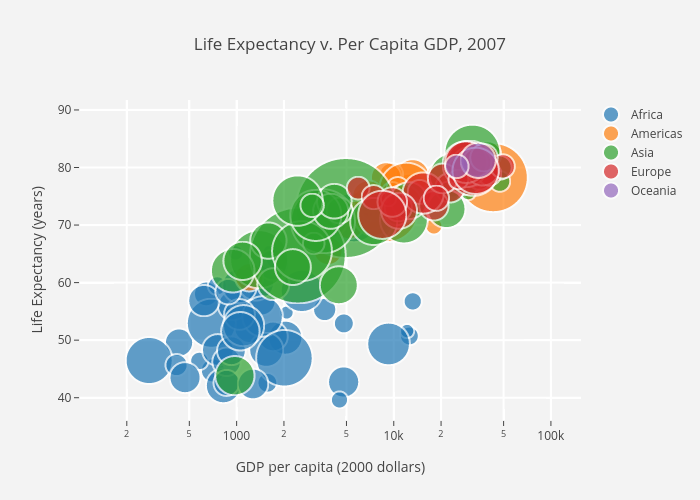
اکنون به بررسی کد می‌پردازیم. ابتدا pyplot مربوط به Matplotlib را با نام مستعار plt ایمپورت می‌کنیم. برای ایجاد شکل نمودار جدید باید ()plt.subplots را فراخوانی کنیم. داده‌های محور x و محور y را به تابع ارسال می‌کنیم و سپس آن‌ها را به ()ax.scatter می‌فرستیم تا نمودار پراکندگی رسم شود. همچنین اندازه نقطه، رنگ نقطه و شفافیت آلفا را تنظیم می‌کنیم. حتی می‌توانیم محور x را طوری تنظیم کنیم که مقیاس لگاریتمی داشته باشد. سپس برچسب‌های عنوان و محور به طور خاص برای این نمودار تنظیم می‌شوند. این یک تابع با استفاده آسان است که یک نمودار پراکندگی را از اول تا آخر برای ما می‌سازد.

import matplotlib.pyplot as plt
import numpy as np

def scatterplot(x_data, y_data, x_label="", y_label="", title="", color = "r", yscale_log=False):

    # Create the plot object
    _, ax = plt.subplots()

    # Plot the data, set the size (s), color and transparency (alpha)
    # of the points
    ax.scatter(x_data, y_data, s = 10, color = color, alpha = 0.75)

    if yscale_log == True:
        ax.set_yscale('log')

    # Label the axes and provide a title
    ax.set_title(title)
    ax.set_xlabel(x_label)
    ax.set_ylabel(y_label)

نمودارهای خطی

«نمودارهای خطی» (Line Plots) بهترین کاربردشان در زمانی که است که می‌بینیم یک متغیر به صورتی هماهنگ با متغیر دیگر حرکت می‌کند، یعنی بین دو متغیر همبستگی بالایی وجود دارد. در تصویر زیر نمونه‌ای از یک نمودار خطی را مشاهده می‌کنید. به وضوح می‌توان دید که مقدار زیادی از تغییر در درصدها در طی زمان برای همه رشته‌ها وجود دارد. ترسیم این داده‌ها با استفاده از نمودار پراکندگی ممکن است منجر به نتیجه کاملاً شلوغ و به هم ریخته شود و درک آن را دشوار ساخته و مانع دیدن روندها شود. نمودارهای خطی در این گونه موقعیت‌ها کاملاً مناسب هستند، زیرا مروری سریع از کوواریانس دو متغیر (درصد و زمان) در اختیار ما قرار می‌دهند. در این مورد نیز می‌توانیم از گروه‌بندی بر مبنای کدگذاری رنگی استفاده کنیم. نمودارهای خطی در تصویر نخست این مقاله در دسته «over-time» قرار می‌گیرند.

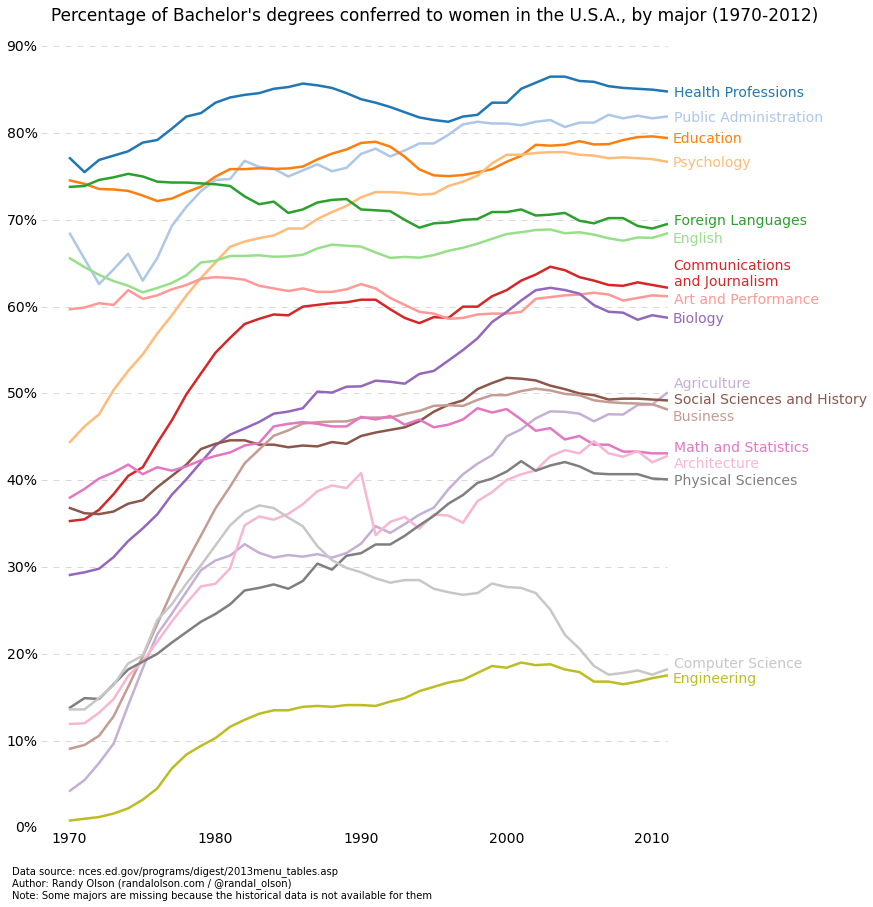
در ادامه کد این نمودار خطی را می‌بینید که کاملاً مشابه نمودار پراکندگی قبلی است. تنها برخی تغییرات کوچک در برخی متغیرها صورت گرفته است:

def lineplot(x_data, y_data, x_label="", y_label="", title=""):
    # Create the plot object
    _, ax = plt.subplots()

    # Plot the best fit line, set the linewidth (lw), color and
    # transparency (alpha) of the line
    ax.plot(x_data, y_data, lw = 2, color = '#539caf', alpha = 1)

    # Label the axes and provide a title
    ax.set_title(title)
    ax.set_xlabel(x_label)
    ax.set_ylabel(y_label)

هیستوگرام

نمودارهای «هیستوگرام» (Histogram) برای دیدن (یا در واقع کشف) توزیع نقاط داده‌ای مفید هستند. در هیستوگرام زیر شاهد ترسیم هیستوگرام فراوانی در برابر IQ هستید. به وضوح می‌توان دید که تراکم در سمت مرکزی نمودار است و میانه نیز در آنجا قرار دارد. همچنین می‌بینیم که از توزیع گائوسی پیروی می‌کند. با استفاده از میله (به جای مثلاً نقاط پراکندگی) می‌توانیم بصری‌سازی کاملاً واضحی از تفاضل نسبی بین فراوانی هر «دسته» (bin) ارائه کنیم. استفاده از دسته‌ها (گسسته‌سازی) به ما کمک می‌کند که تصویری بزرگ‌تر داشته باشیم، به طوری که اگر از همه نقاط داده‌ای بدون دسته‌های گسسته استفاده کنیم، نویز زیادی در بصری‌سازی وجود خواهد داشت و دیدن روندها دشوارتر می‌شود.

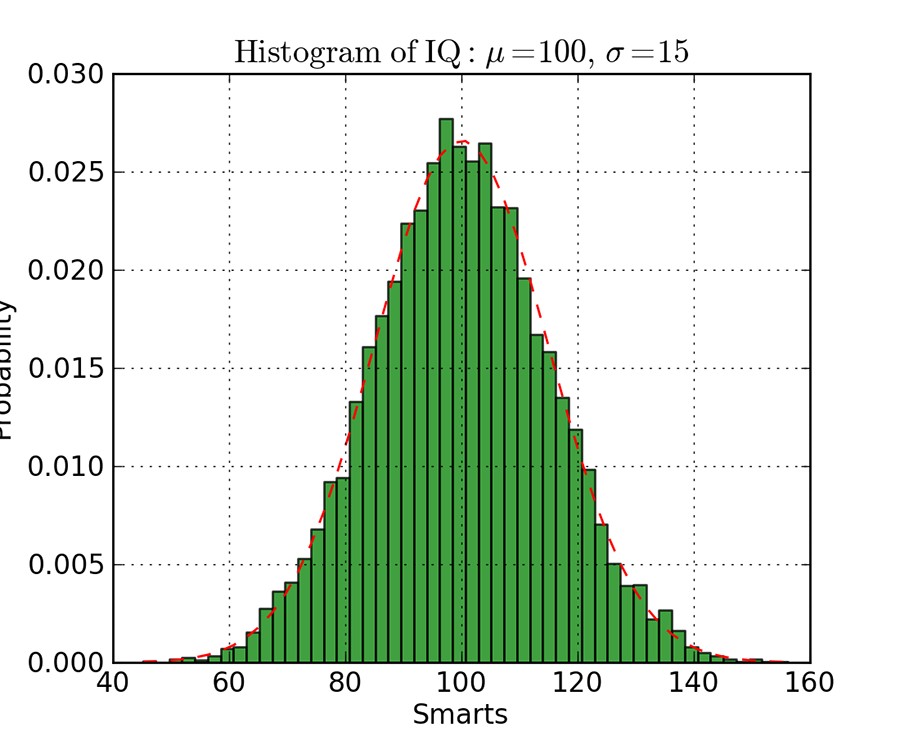
در ادامه کد نمودار هیستوگرام در Matplotlib ارائه شده است. دو پارامتر وجود دارند که باید به آن‌ها توجه کنید. ابتدا پارامترهای n_bins هستند که تعداد دسته‌های گسسته هیستوگرام را تعیین می‌کنند. دسته‌های بیشتر اطلاعاتی ظریف‌تر در اختیار ما قرار می‌دهند اما می‌توانند نویز را نیز وارد نمودار بکنند و ما را از تصویر بزرگ‌تر دور سازند. از سوی دیگر دسته‌های کوچک‌تر دیدی کلی‌نگرتر به ما می‌دهند. بدین ترتیب تصویری بزرگ از آن چه در حال وقوع است در اختیار ما قرار می‌دهند و همچنین جزییات ظریف‌تر را پنهان می‌سازند. در وهله دوم پارامتر cumulative است که یک مقدار بولی است و به ما امکان می‌دهد تا انتخاب کنیم هیستوگرام تجمعی باشد یا نه. بدین ترتیب اساساً انتخاب می‌کنیم که هیستوگرام به صورت «تابع چگالی توزیع» (Probability Density Function | PDF) و یا «تابع چگالی تجمعی» (Cumulative Density Function | CDF) باشد.

def histogram(data, n_bins, cumulative=False, x_label = "", y_label = "", title = ""):
    _, ax = plt.subplots()
    ax.hist(data, n_bins = n_bins, cumulative = cumulative, color = '#539caf')
    ax.set_ylabel(y_label)
    ax.set_xlabel(x_label)
    ax.set_title(title)

تصور کنید می‌خواهید توزیع دو متغیر را در داده‌ها مقایسه کنید. ممکن است فکر کنید باید دو هیستوگرام مجزا تهیه کرده و در کنار هم قرار دهید، اما روش بهتری نیز وجود دارد. می‌توانید هیستوگرام‌ها را با شفافیت متفاوت روی هم قرار دهید. در تصویر زیر توزیع Uniform دارای شفایت 0.5 است و از این رو می‌توانیم زیر آن را ببینیم. بدین ترتیب می‌توانیم مستقیماً دو توزیع را در یک تصویر مشاهده کنیم.

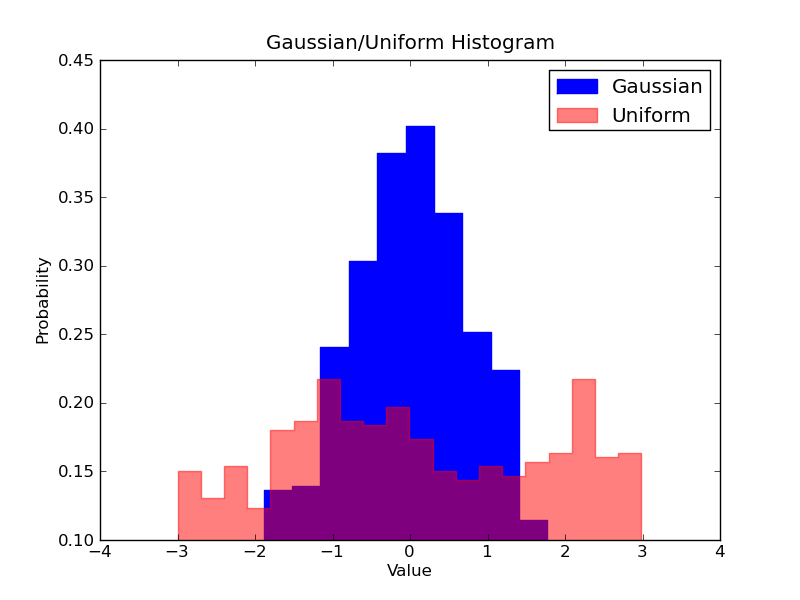
برای رسم هیستوگرام‌های روی هم چند نکته را باید مد نظر داشت. ابتدا باید بازه افقی را طوری تعیین کنیم که شکل هر دو توزیع متغیر باشد. بر اساس این بازه و عدد مطلوب دسته‌ها می‌توانیم عرض هر دسته را محاسبه کنیم. در نهایت دو هیستوگرام را روی یک نمودار واحد قرار می‌دهیم، به طوری که یکی از آن‌ها کمی شفاف‌تر باشد.

# Overlay 2 histograms to compare them
def overlaid_histogram(data1, data2, n_bins = 0, data1_name="", data1_color="#539caf", data2_name="", data2_color="#7663b0", x_label="", y_label="", title=""):
    # Set the bounds for the bins so that the two distributions are fairly compared
    max_nbins = 10
    data_range = [min(min(data1), min(data2)), max(max(data1), max(data2))]
    binwidth = (data_range[1] - data_range[0]) / max_nbins


    if n_bins == 0
    	bins = np.arange(data_range[0], data_range[1] + binwidth, binwidth)
    else: 
    	bins = n_bins

    # Create the plot
    _, ax = plt.subplots()
    ax.hist(data1, bins = bins, color = data1_color, alpha = 1, label = data1_name)
    ax.hist(data2, bins = bins, color = data2_color, alpha = 0.75, label = data2_name)
    ax.set_ylabel(y_label)
    ax.set_xlabel(x_label)
    ax.set_title(title)
    ax.legend(loc = 'best')

نمودارهای میله‌ای

«نمودارهای میله‌ای» (Bar Plots) در مواردی به کار می‌آیند که می‌خواهید داده‌های دسته‌بندی‌شده را که چند دسته محدود دارند (احتمالاً کمتر از 10) بصری‌سازی کنید. اگر تعداد دسته‌ها زیاد باشد در این صورت میله‌ها در تصویر بسیار شلوغ می‌شوند و درک آن دشوار می‌شود. این نوع از نمودارها برای داده‌های دسته‌بندی‌شده مناسب هستند، زیرا می‌توان به سهولت تفاضل بین دسته‌ها را بر مبنای اندازه میله مشاهده کرد. دسته‌ها را می‌توان به سادگی تقسیم‌بندی کرده و با رنگ کدگذاری نیز کرد. 3 نوع مختلف از نمودارهای میله‌ای وجود دارند که در ادامه مورد بررسی قرار می‌دهیم: معمولی، گروه‌بندی‌شده و پشته‌ای. همراه با توضیح هر کدام می‌توانید تصاویر زیر را نیز بررسی کنید.

نمودار میله‌ای معمولی در تصویر نخست زیر قابل مشاهده است. در تابع barplot()‎ مقدار x_data نماینده مقیاس روی محور x و y_data نماینده مقیاس‌بندی روی محور ارتفاع یا محور y است. میله خطا خطی اضافه است که در مرکز هر میله قرار می‌گیرد و می‌تواند برای نمایش انحراف معیار مورد استفاده قرار گیرد.

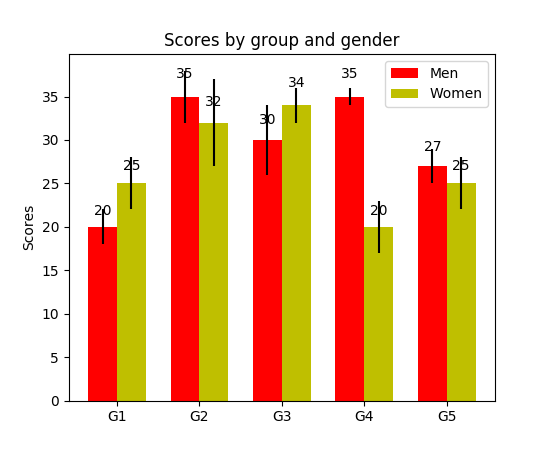
نمودارهای میله‌ای گروه‌بندی‌شده امکان مقایسه چند متغیر دسته‌بندی‌شده را فراهم می‌سازند. در تصویر دوم زیر یک نمودار میله‌ای گروه‌بندی‌شده را می‌بینید. متغیر نخست که مورد مقایسه قرار می‌دهیم میزان تغییرت نمره‌ها بر اساس گروه (گروه‌های G1 ،G2، و غیره) است. همچنین خود جنسیت‌ها را با کدهای رنگی مقایسه می‌کنیم. با بررسی کد می‌بینیم که متغیر y_data_list اینک در عمل لیستی از لیست‌ها است که در آن هر لیست فرعی نماینده گروه متفاوتی است. سپس روی هر گروه، حلقه‌ای تعریف می‌کنیم و برای هر گروه یک میله برای هر مقیاس روی محور x رسم می‌کنیم. همچنین هر گروه با رنگ کدگذاری شده است.

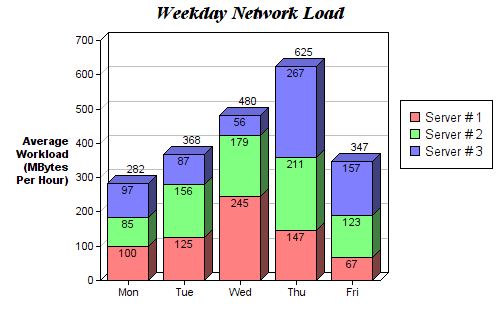
نمودارهای میله‌ای پشته‌ای برای بصری‌سازی مجموعه‌ای دسته‌بندی‌شده از متغیرهای مختلف مناسب هستند. در نمودار میله‌ای پشته‌ای زیر به مقایسه بار سرور در روز‌های مختلف می‌پردازیم. با پشته‌های کدگذاری شده با رنگ نیز می‌توانیم ببینیم و درک کنیم که کدام سرور در هر روز بیشترین کار را انجام داده است و بار در مقایسه با سرورهای دیگر در همه روزها چگونه بوده است. کد این بخش از همان استایل نمودار میله‌ای گروه‌بندی‌شده تبعیت می‌کند. روی همه گروه‌ها حلقه‌ای تعریف می‌کنیم. با استفاده از این زمان، میله‌های جدیدی روی هر یک از میله‌های قدیمی به جای رسم کنار آن‌ها، ترسیم می‌کنیم.

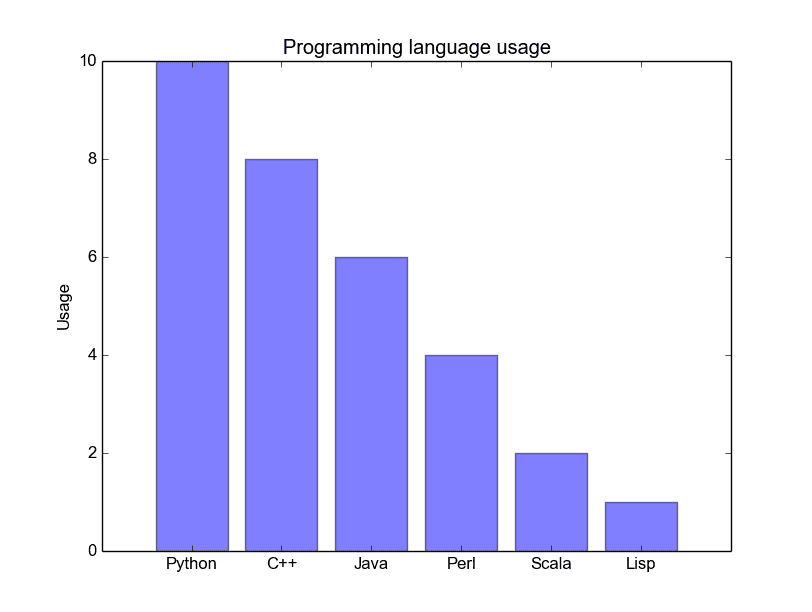
def barplot(x_data, y_data, error_data, x_label="", y_label="", title=""):
    _, ax = plt.subplots()
    # Draw bars, position them in the center of the tick mark on the x-axis
    ax.bar(x_data, y_data, color = '#539caf', align = 'center')
    # Draw error bars to show standard deviation, set ls to 'none'
    # to remove line between points
    ax.errorbar(x_data, y_data, yerr = error_data, color = '#297083', ls = 'none', lw = 2, capthick = 2)
    ax.set_ylabel(y_label)
    ax.set_xlabel(x_label)
    ax.set_title(title)



def stackedbarplot(x_data, y_data_list, colors, y_data_names="", x_label="", y_label="", title=""):
    _, ax = plt.subplots()
    # Draw bars, one category at a time
    for i in range(0, len(y_data_list)):
        if i == 0:
            ax.bar(x_data, y_data_list[i], color = colors[i], align = 'center', label = y_data_names[i])
        else:
            # For each category after the first, the bottom of the
            # bar will be the top of the last category
            ax.bar(x_data, y_data_list[i], color = colors[i], bottom = y_data_list[i - 1], align = 'center', label = y_data_names[i])
    ax.set_ylabel(y_label)
    ax.set_xlabel(x_label)
    ax.set_title(title)
    ax.legend(loc = 'upper right')



def groupedbarplot(x_data, y_data_list, colors, y_data_names="", x_label="", y_label="", title=""):
    _, ax = plt.subplots()
    # Total width for all bars at one x location
    total_width = 0.8
    # Width of each individual bar
    ind_width = total_width / len(y_data_list)
    # This centers each cluster of bars about the x tick mark
    alteration = np.arange(-(total_width/2), total_width/2, ind_width)

    # Draw bars, one category at a time
    for i in range(0, len(y_data_list)):
        # Move the bar to the right on the x-axis so it doesn't
        # overlap with previously drawn ones
        ax.bar(x_data + alteration[i], y_data_list[i], color = colors[i], label = y_data_names[i], width = ind_width)
    ax.set_ylabel(y_label)
    ax.set_xlabel(x_label)
    ax.set_title(title)
    ax.legend(loc = 'upper right')

نمودار جعبه‌ای

در بخش‌های قبلی هیستوگرام‌ها را دیدیم که برای بصری‌سازی توزیع متغیرها عالی هستند. اما اگر بخواهیم اطلاعات بیشتری از این به دست آوریم چطور؟ شاید بخواهیم دید روشنی از انحراف معیار به دست آوریم. یا شاید میانه اختلاف زیادی با میانگین داشته باشد و نقاط دوردست (outliers) زیادی داشته باشیم. اگر میزان چولگی زیاد باشد و بسیاری از مقادیر در یک سمت متراکم شوند چطور؟

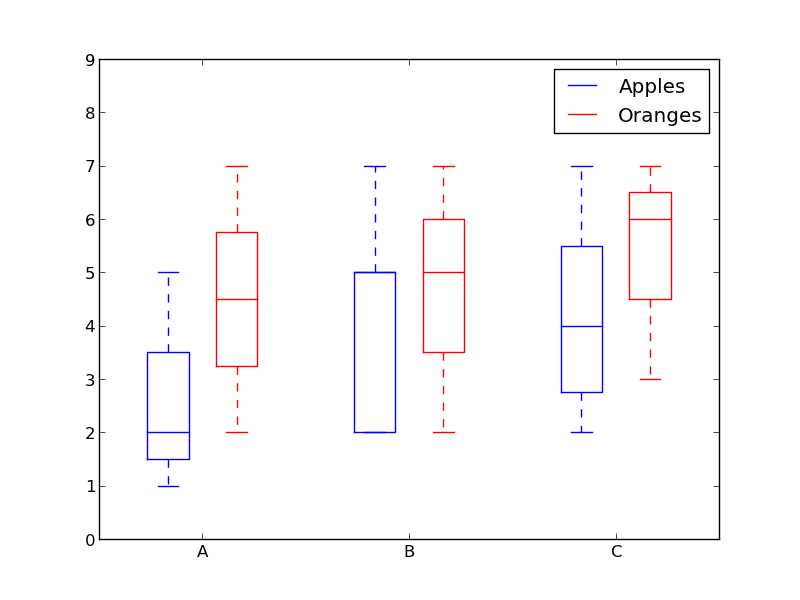
در این حالت‌ها از «نمودار جعبه‌ای» (Box Plots) استفاده می‌کنیم. نمودارهای جعبه‌ای همه اطلاعات فوق را در اختیار ما قرار می‌دهند. بخش تحتانی و فوقانی جعبه‌ها با خط پیوسته همواره چارک‌های اول و سوم (یعنی 25 و 75 درصد داده‌ها) هستند و نوار درون کادر نیز همواره چارک دوم (میانه) را نمایش می‌دهد. خطوط نقطه‌چین که از جعبه بیرون زده‌اند نیز بازه داده‌ها را نمایش می‌دهند.

از آنجا که نمودار جعبه‌ای برای هر گروه/متغیر رسم می‌شود، تنظیم آن بسیار آسان است. x_data لیست گروه‌ها/متغیرها است. تابع Matplotlib به نام ()boxplot یک نمودار جعبه‌ای برای هر ستون y_data یا هر بردار در دنباله y_data می‌سازد. از این رو هر مقدار در x_data متناظر با یک ستون/بردار در y_data است. بنابراین تنها کاری که باید انجام دهیم، تنظیم جنبه‌های تزیینی نمودار است.

def boxplot(x_data, y_data, base_color="#539caf", median_color="#297083", x_label="", y_label="", title=""):
    _, ax = plt.subplots()

    # Draw boxplots, specifying desired style
    ax.boxplot(y_data
               # patch_artist must be True to control box fill
               , patch_artist = True
               # Properties of median line
               , medianprops = {'color': median_color}
               # Properties of box
               , boxprops = {'color': base_color, 'facecolor': base_color}
               # Properties of whiskers
               , whiskerprops = {'color': base_color}
               # Properties of whisker caps
               , capprops = {'color': base_color})

    # By default, the tick label starts at 1 and increments by 1 for
    # each box drawn. This sets the labels to the ones we want
    ax.set_xticklabels(x_data)
    ax.set_ylabel(y_label)
    ax.set_xlabel(x_label)
    ax.set_title(title)

سخن پایانی

در این راهنما 5 روش بصری‌سازی داده‌ها با استفاده از کتابخانه Matplotlib پایتون را توضیح دادیم. انتزاع این بصری‌سازی‌ها در تابع‌ها موجب می‌شود که کد شما خوانش آسان‌تری بیابد. امیدواریم این نوشته برای شما مفید بوده باشد و مطالب جدید و کارآمدی از آن آموخته باشید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌نویسی پایتون
• مجموعه آموزش‌های برنامه‌‌نویسی
• گنجینه آموزش های برنامه نویسی پایتون (Python)
• اینفوگرافیک چیست و چه فرقی با بصری سازی داده‌ها دارد؟
• زبان برنامه نویسی پایتون (Python) — از صفر تا صد

==