برنامه تشخیص اعداد اول در پایتون — به زبان ساده

«عدد اول» (Prime Numbers)، عددی طبیعی و بزرگ‌تر از یک است که جز یک و خودش، بر هیچ عدد دیگری بخش‌پذیر نباشد. برای مطالعه بیشتر پیرامون اعداد اول، مطلب «اعداد اول — به زبان ساده» توصیه می‌شود. در این مطلب، هدف ارائه روشی برای نوشتن برنامه تشخیص اعداد اول در پایتون است. برای تشخیص اعداد اول، راهکارهای گوناگونی وجود دارد که یکی از محبوب‌ترین آن‌ها، ‌«غربال اراتوستن» (Sieve of Eratosthenes) است. غربال اراتوستن، یکی از روش‌های باستانی برای یافتن همه اعداد اول کوچک‌تر از یک عدد مشخص (مثلا n) است. روش کار به این صورت است که اعداد اول (از دو تا جذر n) یافته می‌شوند و مضارب آن‌ها (غیر از خودشان) خط می‌خورند. اعداد خط نخورده، همگی اول هستند. برای مثال، فرض می‌شود هدف پیدا کردن اعداد اول از ۱ تا n = ۱۰۰ است. با استفاده از غربال اراتوستن، به صورت زیر عمل می‌شود:

1. همه اعداد از ۱ تا ۱۰۰ را می‌نویسیم.
2. عدد ۱ را خط می‌زنیم.
3. دور عدد ۲ خط می‌کشیم (عدد اول است) و همه مضرب‌هایش را خط می‌زنیم.
4. دور عدد اول بعدی (در اینجا ۳) خط می‌کشیم و همه مضرب‌هایش را خط می‌زنیم.
5. به مرحله ۴ باز می‌گردیم و آن مرحله را تکرار می‌کنیم.
6. مراحل بالا را تا جایی که عدد اولی پیدا شود که مضرب‌هایش در جدول خط نخورده باشد، ادامه می‌دهیم.
7. اعداد باقی‌مانده (که خط نخورده‌اند) عدد اول هستند.

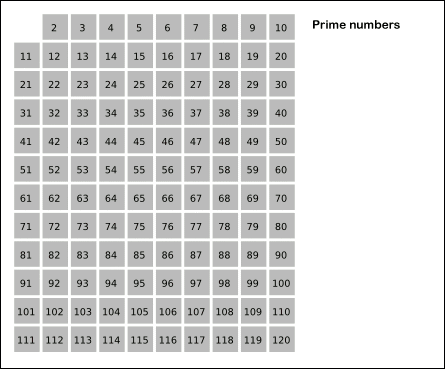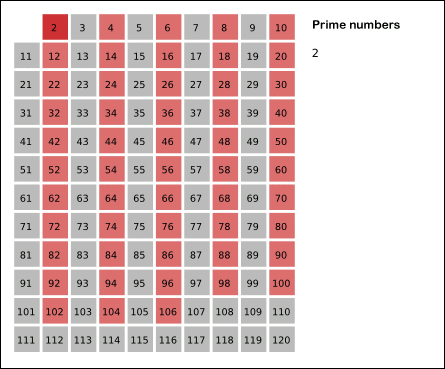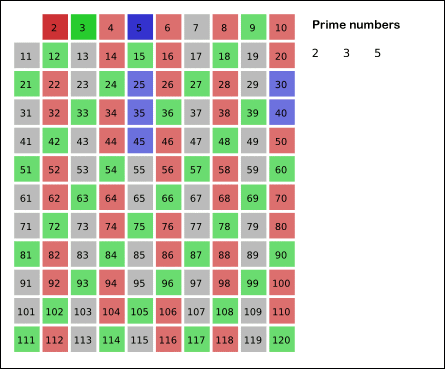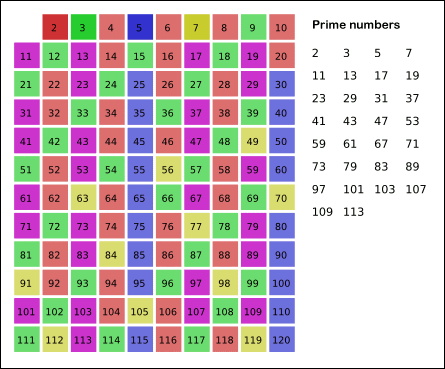
البته، با توجه به اینکه یک عامل بزرگتر از n باید مضرب یک عامل کوچک‌تر باشد که در حال حاضر بررسی شده است، بررسی تا n√ بهینه‌تر از چک کردن تا n است. راهکارهای بهتری نیز برای تشخیص اعداد اول وجود دارند. در ادامه، با بهره‌گیری یک روش دیگر، برنامه تشخیص اعداد اول در پایتون نوشته شده است.

برنامه تشخیص اعداد اول در پایتون

فرض می‌شود عدد صحیح مثبت N داده شده است. هدف، نوشتن برنامه‌ای در پایتون است که تعیین می‌کند یک عدد اول است یا خیر. عدد اول، یک عدد طبیعی بزرگ‌تر از ۱ است که به جز خودش و ۱، هیچ مقسوم‌علیه مثبت دیگری ندارد. اولین اعداد اول عبارتند از {… ,11 ,7 ,5 ,3 , 2}.

مثال:

ورودی: n=11

خروجی: درست (true)



ورودی: n=15

خروجی: غلط (false)



ورودی: n=1

خروجی: غلط (false)

در حال حاضر، هدف حل کردن این مساله به وسیله روش تکرار شونده است. کار به این صورت انجام می‌شود که با شروع از ۲ تا n/2 و با استفاده از یک حلقه for، تکرار در همه اعداد انجام و بررسی می‌شود که آیا n بر عددی در این بازه تقسیم‌پذیر است یا خیر. اگر عددی پیدا شد که n بر آن تقسیم‌پذیر بود، مقدار «false» بازگردانده می‌شود. اگر هیچ عددی بین ۲ و n/2 یافت نشد که n بر آن تقسیم‌پذیر باشد، بدین معنا است که n عدد اول است و مقدار «True» بازگردانده می‌شود. در ادامه، برنامه تشخیص اعداد اول در پایتون ارائه شده است.

# Python program to check if  
# given number is prime or not 
  
num = 11
  
# If given number is greater than 1 
if num > 1: 
      
   # Iterate from 2 to n / 2  
   for i in range(2, num//2): 
         
       # If num is divisible by any number between  
       # 2 and n / 2, it is not prime  
       if (num % i) == 0: 
           print(num, "is not a prime number") 
           break
   else: 
       print(num, "is a prime number") 
  
else: 
   print(num, "is not a prime number")

خروجی:

11 is a prime number

بهبود برنامه تشخیص اعداد اول در پایتون

می‌توان برنامه تشخیص اعداد اول در پایتون را با بهره‌گیری از راهکارهای زیر، بهبود بخشید.

1. با توجه به اینکه یک عامل بزرگتر از n باید مضرب یک عامل کوچک‌تر باشد که در حال حاضر بررسی شده است، به جای n، تا n√ بررسی می‌شود.
2. الگوریتم را می‌توان با توجه به اینکه همه اعداد اول به استثنای ۲ و ۳، به شکل 6k ± 1 هستند، بهبود داد. این امر بدین دلیل است که همه اعداد صحیح را می‌توان به صورت 6k + i برای عدد صحیح k و $$i = -1, 0, 1, 2, 3$$ یا ۴، نشان داد. همانطور که پیش‌تر بیان شد، ۲ و ۳ استثنا هستند. عدد ۲ بر (6k + 0) ،(6k + 2) ،(6k + 4) و ۳ بر (6k + 3) بخش‌پذیر است. بنابراین، یک روش کارآمدتر آن است که بررسی شود آیا n بر ۲ یا ۳ بخش‌پذیر است یا نه و سپس، برای همه اعداد به شکل 6k ± 1 بررسی شود.

# A optimized school method based  
# Python3 program to check 
# if a number is prime 
  
  
def isPrime(n) : 
  
    # Corner cases 
    if (n <= 1) : 
        return False
    if (n <= 3) : 
        return True
  
    # This is checked so that we can skip  
    # middle five numbers in below loop 
    if (n % 2 == 0 or n % 3 == 0) : 
        return False
  
    i = 5
    while(i * i <= n) : 
        if (n % i == 0 or n % (i + 2) == 0) : 
            return False
        i = i + 6
  
    return True
  
  
# Driver Program  
if (isPrime(11)) : 
    print(" true") 
else : 
    print(" false") 
      
if(isPrime(15)) : 
    print(" true") 
else :  
    print(" false") 
      
      
# This code is contributed  
# by Nikita Tiwari.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• حل مساله رنگ‌آمیزی گراف با الگوریتم پس گرد — به زبان ساده
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^