تولید عدد تصادفی با یک تاس شش وجهی — به زبان ساده

پیش از این، در مطلب «اعداد تصادفی (Random Numbers) — تاریخچه و کاربردها» به مفهوم اعداد تصادفی، تاریخچه تولید آن‌ها، انواع اعداد تصادفی، الگوریتم‌های تولید اعداد شبه‌تصادفی و کاربرد اعداد تصادفی پرداخته شد. همچنین، در مطلب دیگری با عنوان «تولید اعداد تصادفی در پایتون — به زبان ساده» به چگونگی تولید انواع اعداد تصادفی در پایتون پرداخته شد. در این مطلب، روش تولید عدد تصادفی با یک تاس شش وجهی مورد بررسی قرار می‌گیرد.

تولید عدد تصادفی با یک تاس شش وجهی

برای تولید عدد تصادفی بین ۱ تا ۱۰ با یک تاس شش‌وجهی، باید به روش زیر عمل کرد:

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

1. تاس را N بار پرتاب کنید و مجموع شماره‌های مشاهده شده از تاس‌ها (S) را محاسبه کنید.
2. باقیمانده تقسیم این مجموع (یعنی S) بر ۱۰ را محاسبه و سپس یک واحد به آن اضافه کنید.
3. هنگامی که N به بی‌نهایت میل می‌کند (∞→?)، خروجی مرحله پیشین به عددی با توزیع یکنواخت در بازه [۱,۱۰] میل می‌کند.

برای مثال، فرض می‌شود که تاس سه مرتبه پرتاب شده است. پس N = ۳ پرتاب انجام شده که نتیجه اعداد مشاهده شده، ۷، ۳ و ۵ است. مجموع این اعداد برابر با ۱۵ (S = 15) خواهد بود. باقیمانده تقسیم ۱۵ بر ۱۰، برابر با ۵ است. با افزودن یک واحد به ۵، عدد ۶ حاصل می‌شود که خروجی تصادفی مورد انتظار است.

پرسشی که ممکن است در این وهله مطرح شود آن است که «با توجه به قضیه حد مرکزی، توزیع مجموع یا میانگین پدیده‌های تصادفی مستقل و هم‌توزیع، فارغ از توزیع اولیه آزمایش، وقتی تعداد تکرارها به سمت بی‌نهایت میل کند، توزیع نرمال خواهد بود. پس چرا در اینجا گفته می‌شود که توزیع نهایی یکنواخت است؟».

برنامه زیر، که در متلب نوشته شده است، معادل ده هزار بار پرتاب یک تاس و تکرار همین موضوع به اندازه ده هزار بار است.

1t = randi([1,6], 10000, 10000);
2S = sum(t);
3R = mod (S, 10) + 1;
4histogram(R);

همان طور که در شکل زیر دیده می‌شود، خروجی این فرایند بسیار نزدیک به توزیع یکنواخت است که با افزایش تعداد پرتاب‌ها، به توزیع یکنواخت میل خواهد کرد. مشخص است که در ۱۰ هزار بار پرتاب هر یک از اعداد ۱ تا ۱۰ باید بطور متوسط هزار بار مشاهده شوند. این موضوع در نمودار زیر به خوبی دیده می‌شود.

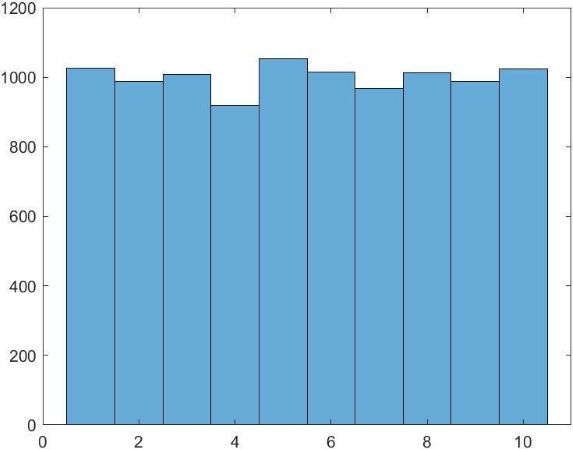
اما طبق قضیه حد مرکزی، متغیری که دارای توزیع نرمال خواهد بود، S یا مجموع مقادیر مشاهده شده طی پرتاب‌ها است. شایان توجه است که برای محاسبه R، از باقی‌مانده‌ تقسیم استفاده شده است. طبق شکل زیر، توزیع آماری متغیر S نزدیک به توزیع نرمال (گوسی) است.

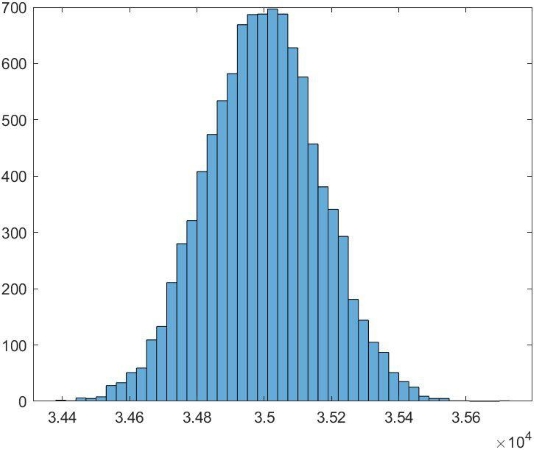
در واقع، استفاده از باقیمانده، موجب تغییر توزیع داده‌ها می‌شود.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

زیرا، مستقل از توزیع اعداد، باقیمانده‌های آن‌ها برای هر مقسوم‌علیه (در اینجا ۱۰ در نظر گرفته شده) با توزیع یکنواخت توزیع شده‌اند.

اگر مطلب بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های داده‌کاوی و یادگیری ماشین
• زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد
• یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
• پیاده‌سازی الگوریتم‌های یادگیری ماشین با پایتون و R — به زبان ساده
• اعداد تصادفی (Random Numbers) — تاریخچه و کاربردها

^^