ادغام k آرایه مرتب – راهنمای کاربردی

K آرایه مرتب شده داده شده است. هر آرایه دارای اندازه N است. هدف ادغام k آرایه مرتب شده در یک آرایه مرتب است. مثال زیر در این رابطه جالب توجه است.

Input : arr[][] = {{5, 7, 15, 18},
                   {1, 8, 9, 17},
                   {1, 4, 7, 7}}
Output :  {1, 1, 4, 5, 7, 7, 7, 8, 9, 15, 17, 18}

Input : arr[][] = {{3, 2, 1}
                   {6, 5, 4}}
Output :  {1, 2, 3, 4, 5, 6}

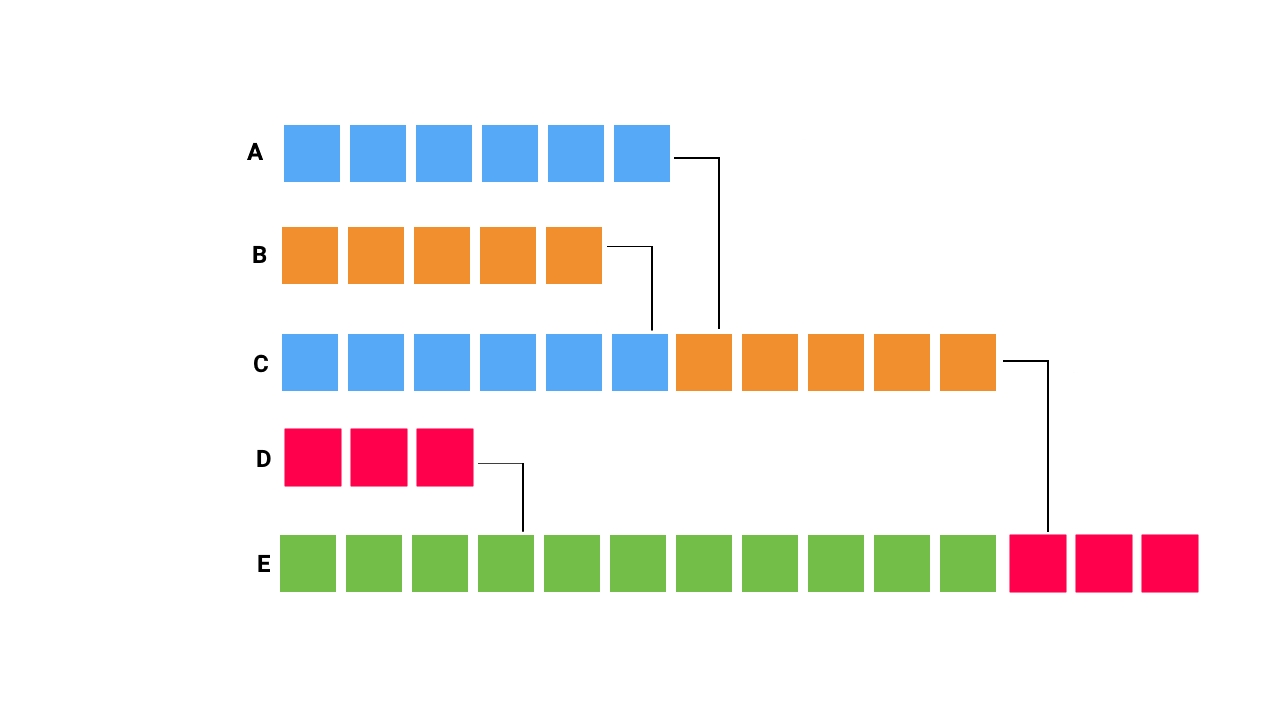
برای درک بهتر این مطلب، نیاز به آشنایی با «الگوریتم مرتب‌سازی ادغامی» (Merge Sort) است. یک راهکار ساده برای ادغام k آرایه مرتب شده، الحاق همه آرایه‌ها، یکی پس از دیگری و سپس، مرتب‌سازی آن‌ها است. پیچیدگی زمانی این عملیات از درجه O(N*k * log(N*k))‎ است. در روش موثرتر، به K آرایه، به عنوان یک حالت متوسط از الگوریتم مرتب‌سازی ادغامی نگاه می‌شود.

فیلم آموزش طراحی الگوریتم + حل مثال های عملی در فرادرس

کلیک کنید

از آنجا که K آرایه مرتب شده در حال حاضر وجود دارد، تنها نیاز به ادغام کردن K آرایه است. با ادغام آن‌ها، یک درخت بازگشتی با ارتفاع log(k)‎ ساخته می‌شود که در هر گام از آن، تعداد آرایه‌های باقیمانده نصف می‌شود. در هر ارتفاعی، الگوریتم به مدت O(N*k)‎ به طول خواهد انجامید. بنابراین، پیچیدگی زمانی کاهش پیدا می‌کند و برابر با O( N*k * log(k) )‎ خواهد بود.

الگوریتم ادغام k آرایه مرتب شده

1. آرایه خروجی با اندازه  N*k را مقداردهی اولیه کن.
2. تابع divide را فراخوانی کن. با l و r، طیف آرایه‌هایی که ادغام می‌شوند را نمایش بده و بنابراین بین 0 تا k-1 متغیر باش.
3. در هر گام، نیمه سمت چپ و راست دامنه به صورت بازگشتی فراخوانی می‌شود، بنابراین این‌ها مرتب‌سازی می‌شوند و در آرایه خروجی نیز مرتب می‌شوند.
4. پس از آن، نیمه سمت راست و چپ ادغام می‌شوند. برای ادغام کردن، نیاز به تعیین دامنه اندیس‌ها برای نیمه‌های سمت راست و چپ در آرایه خروجی است. می‌توان به سادگی این مورد را پیدا کرد.
   • بگذار بخش سمت چپ از اندیس  l * n از آرایه خروجی آغاز شود.
   • به طور مشابه، بخش سمت راست از اندیس l + r) / 2 + 1) * n‎)) آرایه خروجی آغاز می‌شود.

همچنین، باید طول بخش‌های سمت راست و چپ تعیین شود. همچنین، باید طول بخش‌های سمت راست و چپ تعیین شود. پس از آن، دو آرایه موقتی «l_arr» و «r_arr» برای ذخیره‌سازی مقادیر از بخش‌های راست و چپ مورد استفاده قرار می‌گیرند. در نهایت، از روش دو اشاره‌گر برای ادغام نتایج در بخش‌های سمت راست و چپ در هنگام اجرای ادغام استفاده می‌شود. در ادامه، پیاده‌سازی الگوریتم بالا ارائه شده است.

برنامه ادغام k آرایه مرتب شده در ++C

برنامه ادغام k آرایه مرتب شده در جاوا

برنامه ادغام k آرایه مرتب شده در پایتون ۳

برنامه ادغام k آرایه مرتب شده در #C

خروجی قطعه کد بالا به صورت زیر است.

1 1 4 5 7 7 7 8 9 15 17 18

این مساله را می‌توان با استفاده از «هرم کمینه» (Min-Heap) نیز حل کرد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^