الگوریتم عامل دورافتاده محلی (Local Outlier Factor) جهت شناسایی داده های پرت — به زبان ساده

الگوریتم «عامل دورافتاده محلی» (Local Outlier Factor | LOF) توسط «مارکوس ام بروئینگ» (Markus M. Breunig)، «هانس پیتر کریگل» (Hans-Peter Kriegel)، «ریموند تی وو» (Raymond T. Ng) و «جورج سندر» (Jörg Sander) در سال ۲۰۰۰ برای کشف ناهنجاریها و دادههای پرت موجود در نقاط داده با اندازهگیری انحراف محلی یک نقطه داده با توجه به همسایههای آن ارائه شد. این الگوریتم (LOF)، در برگیرنده برخی مفاهیم موجود در الگوریتمهای DBSCAN و OPTICS مانند «فاصله از مرکز» (core distance) و «فاصله دسترسیپذیری» (reachability distance) است که برای تخمین چگالی محلی مورد استفاده قرار میگیرند. (برای آشنایی با مفاهیم مورد استفاده در این الگوریتم، مطالعه مطلب «آشنایی با خوشهبندی (Clustering) و شیوههای مختلف آن» توصیه میشود.)
ایده اساسی الگوریتم عامل دورافتاده محلی
الگوریتم عامل دورافتاده محلی بر مبنای مفهوم چگالی محلی بنا شده و در آن محلی بودن بر اساس k نزدیکترین همسایگی تعیین میشود که فاصله آنها برای تخمین چگالی مورد استفاده قرار میگیرد. با مقایسه چگالی محلی یک شی با چگالیهای همسایههای آن میتوان نواحی دارای چگالی مشابه و نقاطی که اساسا چگالی کمتری نسبت به همسایههای خود دارند را تعیین کرد.
این موارد به عنوان دورافتادگی (داده پرت) در نظر گرفته میشوند. چگالی محلی به وسیله فاصله معمولی که یک نقطه داده توسط همسایههای خود «دسترسیپذیر» است تخمین زده میشود.

بیان ریاضی
فرض میشود (k-distance(A فاصله شی A از kاُمین نزدیکترین همسایه است. توجه به این نکته لازم است که مجموعه k نزدیکترین همسایهها شامل همه اشیا موجود در این فاصله است که در صورت وقوع «گره» ممکن است بیش از k شی باشند. مجموعه k نزدیکترین همسایگی به صورت (Nk(A نشان داده میشود.
این فاصله برای آنچه «فاصله دسترسی پذیری» نامیده میشود مورد استفاده قرار میگیرد.
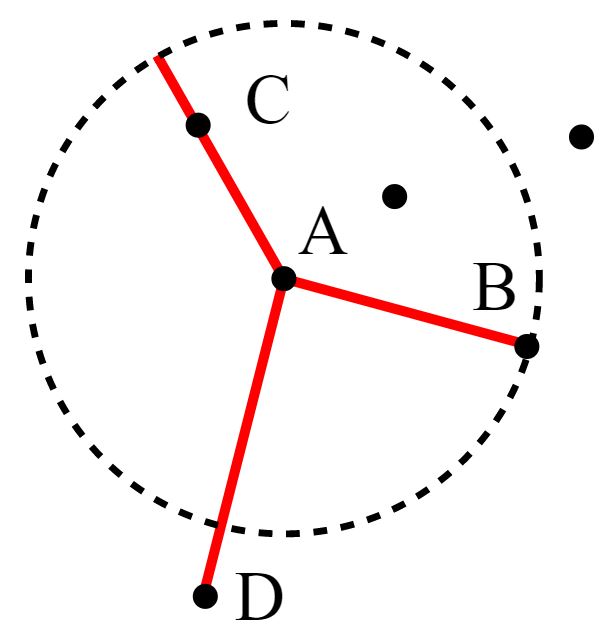
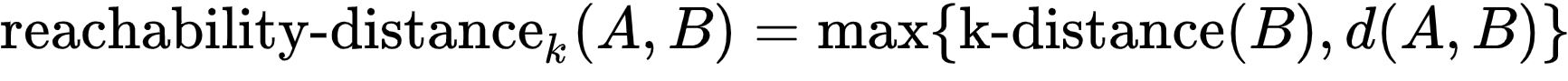
در واقع، فاصله دستریپذیری یک شی A از B فاصله واقعی دو شی و حداقل k-distance از B است. اشیائی که متعلق به k نزدیکترین همسایههای B هستند (مرکز B، تحلیل خوشه DBSCAN) دارای فاصله مساوی در نظر گرفته میشوند. دلیل محاسبه این فاصله گرفتن نتایج پایدارتر است. توجه به این نکته لازم است که فاصله در اینجا با بیان ریاضیاتی آن متفاوت است، زیرا متقارن نیست. (این در حالیست که یک اشتباه متداول آن است که اغلب از k-distance استفاده میشود در حالیکه در صورت استفاده از این رابطه در واقع از روش دیگری استفاده شده که از آن با عنوان Simplified-LOF یاد میشود.). فاصله دسترسیپذیری محلی شی A به صورت زیر تعریف میشود.
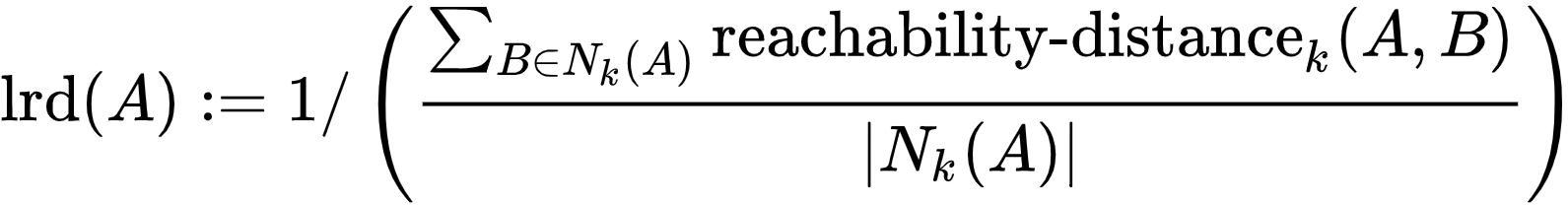
مقدار بیان شده معکوس میانگین دسترسیپذیری شی A از همسایههای آن است. نکته قابل توجه آن است که این مقدار، میانگین دسترسیپذیری همسایهها از A نیست (که در تعریف (k-distance(A است)، بلکه فاصلهای محسوب میشود که A با آن توسط همسایههای خود دسترسیپذیر است. برای نقاط تکراری، این مقدار میتواند بینهایت شود. سپس، چگالیهای دسترسیپذیری محلی با استفاده از فرمول زیر با چگالیهای دسترسیپذیری همسایهها مقایسه میشوند.
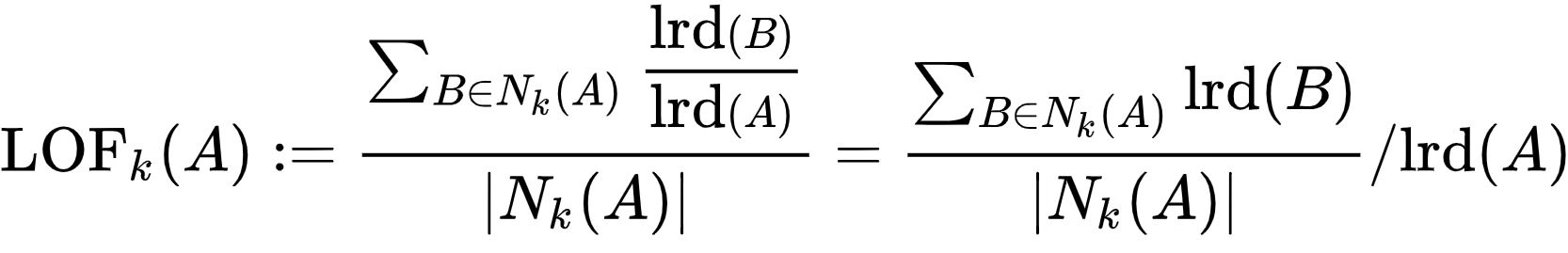
این مقدار برابر است با میانگین چگالی دسترسیپذیری محلی همسایگان تقسیم بر چگالی دسترسیپذیری محلی خود اشیا. مقدار تقریبا برابر ۱ حاکی از آن است که شی با همسایههای آن قابل مقایسه هستند (و بدین ترتیب یک نقطه دورافتاده محسوب نمیشود). مقدار زیر ۱ حکایت از وجود یک ناحیه چگالتر دارد (که به معنای وجود یک شی درون محدوده است)، در حالیکه مقادیری که به طور قابل توجهی از ۱ بزرگتر هستند به عنوان دورافتاده در نظر گرفته میشوند.
مزایا
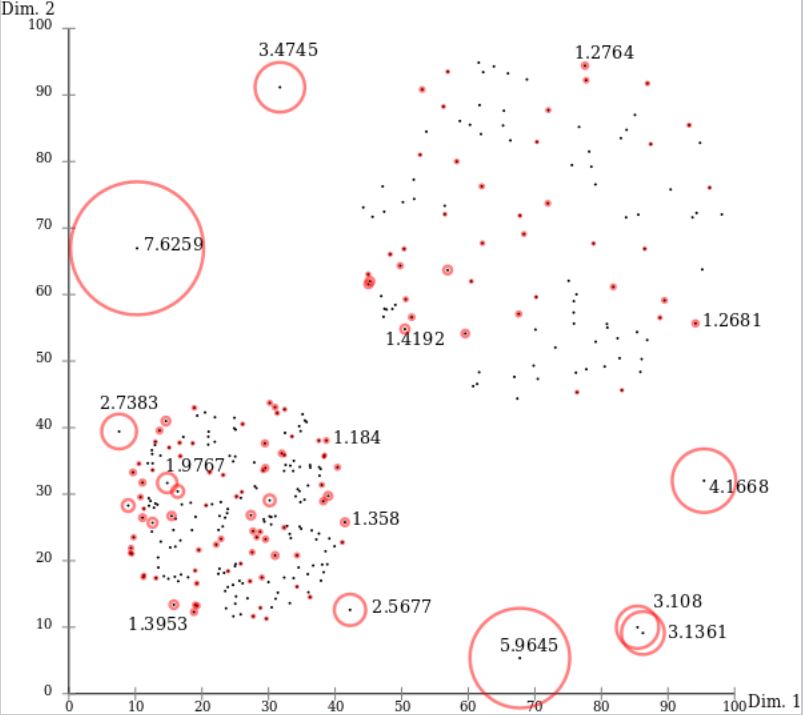
با توجه به رویکرد محلی، LOF قادر به شناسایی دورافتادگیهایی در مجموعه داده است که در ناحیه دیگری از مجموعه داده دورافتاده محسوب نمیشوند. برای مثال، یک نقطه در فاصله «کوچک» از یک خوشه بسیار چگال یک نقطه دورافتاده محسوب میشود، در حالیکه یک نقطه درون خوشهای خلوت ممکن است فاصلهای مشابه با آنچه بیان شد را نسبت به همسایگان خود داشته باشد.
در حالیکه شهود ریاضی LOF تنها قابل اعمال بر فضای بردار ابعاد پایین است، الگوریتم میتواند در هر زمینهای که یک تابع عدم مشابهت قابل تعریف است اعمال شود.به لحاظ تجربی نشان داده شده که این روش با تنظیمات متعدد عملکرد بسیار خوبی دارد، و اغلب در مقایسه با رقبای خود عملکرد بهتری داشته است. برای مثال، در تشخیص نفوذ در شبکه و دادههای بنچمارک دستهبندی پردازش شده از رقبا پیشی گرفته است. خانواده LOF از روشهای به سادگی قابل عمومیسازی و اعمال بر دیگر مسائل مانند شناسایی دورافتادگیها در دادههای جغرافیایی، جریانهای ویدئویی و شبکههای نوشتاری هستند.
معایب و افزونهها
مقادیر نتیجه شده نسبی هستند و تفسیر آنها دشوار است. یک مقدار ۱ یا حتی کمتر از آن حاکی از وجود یک داده درون محدوده است، اما هیچ قاعده واضحی برای هنگامی که نقطهای دور افتاده است وجود ندارد. در یک مجموعه داده، یک مقدار ۱.۱ ممکن است دورافتاده باشد و در یک مجموعه داده و پارامترهای دیگر (با نوسانات محلی)، مقدار ۲ ممکن است همچنان درون محدوده باشد.این تفاوتها ممکن است درون یک مجموعه داده نیز با توجه به محلیت روش به وقوع بپیوندد.
افزونههایی برای الگوریتم LOF وجود دارد که در تلاش برای بهبود LOF از جنبههای زیر هستند:
- بستهبندی ویژگیها برای تشخیص دورافتادگی: LOF را روی تصاویر (projections) چندگانه از ویژگیها اجرا و نتایج را برای بهبود کیفیت تشخیص در ابعاد بالا ترکیب میکند. این اولین رویکرد یادگیری گروهی برای تشخیص ناهنجاری است.
- احتمال دورافتادگی محلی (LoOP): روشی است که از LOF مشتق شده اما از آمارهای کم هزینه محلی برای داشتن حساسیت کمتر روی انتخاب پارامتر k استفاده میکند. علاوه بر این، مقادیر نتیجه شده در رنج مقداری [۱ : ۰] مقیاس میپذیرند.
- تفسیر و متحد کردن امتیازهای دورافتادگی: نرمالسازی امتیازهای LOF در بازه [۱ : ۰] با استفاده از مقیاسپذیری آماری برای افزایش کارآمدی را مطرح میکند و در ایدههای بهبود یافته LoOP قابل مشاهده است.
- در ارزیابی رتبهبندی دورافتادگیها و امتیازهای دورافتادگی: روشهایی را برای اندازهگیری مشابهت و تنوع روشها برای ساخت گروههای تشخیص دورافتادگی پیشرفته با استفاده از انواع LOF و دیگر الگوریتمها و بهبود رویکردهای بستهبندی تشریح شده در بالا مطرح میکند.
- تشخیص دورافتادگی محلی تجدید نظر شده: یک رویکرد عمومی بر محلی بودن با کاربردهایی برای تشخیص دورافتادگی در دادههای فضایی، ویدئویی و شبکه است که الگوهای عمومی در روشهای تشخیص ناهنجاری (شامل LOF، نسخه ساده شده LOF و LoOP) را مورد بحث قرار میدهد و آنها را در یک «چارچوب» (framework) کلی خلاصه میکند. این چارچوب سپس برای شناسایی دورافتادگیها برای مثال در دادههای جغرافیایی، جریانهای ویدئویی و شبکههای نوشتاری مورد استفاده قرار میگیرد.
اگر نوشته بالا برای شما مفید بوده، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- آمار، احتمالات و دادهکاوی
- مجموعه آموزشهای هوش محاسباتی
- مجموعه آموزشهای پیشبینی و تحلیل سریهای زمانی
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- مجموعه آموزشهای مدلسازی، برازش و تخمین
- مجموعه آموزشهای شبکههای عصبی مصنوعی
- معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
^^












