جبر خطی چیست؟ – مفاهیم پایه به زبان ساده

در جبر خطی (Linear Algebra) به مطالعه بردارها و ماتریس‌ها در ابعاد متناهی یا نامتناهی می‌پردازیم. همچنین نگاشت یا تبدیل خطی چنین فضاهایی را می‌توان به عنوان یکی دیگر از موضوعات جبر خطی در نظر گرفت. جبر خطی به عنوان شاخه‌ای از ریاضیات محض و کاربردی در رشته‌‌های دیگری مانند علم داده، فیزیک، هوش مصنوعی، علوم طبیعی و برخی از رشته‌‌های مهندسی نیز کاربرد دارد. در این مطلب از مجله فرادرس توضیح می‌دهیم جبر خطی چیست و مفاهیم پایه آن کدامند.

جبر خطی چیست و چه موضوعاتی در آن مطرح می شود؟

جبر خطی یا Linear Algebra شاخه‌ای از ریاضیات است که در آن می‌آموزیم فضای برداری، بردارها، توابع خطی، سیستم معادلات خطی و ماتریس‌ها چه هستند. به عبارت دیگر، جبر خطی علم مطالعه توابع خطی و بردارها است و توضیح می‌دهد که معادلات خطی چه هستند و چگونه می‌توانیم آن‌ها را در فضای برداری و با استفاده از ماتریس‌ها نمایش دهیم.

هدف ما از مطالعه جبر خطی حل دستگاه‌های معادلات خطی با تعداد محدودی مجهول است و سعی می‌کنیم در این بررسی به پرسش‌های زیر پاسخ دهیم:

• توصیف پاسخ‌ها: آیا برای یک دستگاه معادلات خطی پاسخی وجود دارد؟ چند پاسخ داریم؟
• یافتن پاسخ‌ها: شکل مجموعه‌ پاسخ‌ها چگونه است؟ پاسخ‌ها دقیقا چه هستند؟

کلمه «جبر» در ریاضیات به معنی «روابط» است، پس جبر خطی به معنای «روابط خطی» است. عملیات $$F$$ را در جبر خطی یک عملیات خطی می‌نامیم، هرگاه مقیاس‌های ورودی و خروجی یکسان باشند، یعنی افزودن مقادیر مشخصی به ورودی موجب افزایشی مقادیری برابر در خروجی شود:

$$F (ax) = a .F(x)$$

$$F (x + y) = F(x) + F(y)$$

این شاخه از ریاضیات یکی از بنیادی‌ترین مباحث را شامل می‌شود و مفاهیم هندسه مدرن نیز بر پایه آن توسعه داده شده‌اند. به کمک جبر خطی می‌توانیم بسیاری از پدیده‌های طبیعی را مدل‌سازی کنیم و به همین علت است که در علوم مهندسی نیز کاربردهای گسترده‌ای دارد. مهم‌ترین موضوعاتی که در جبر خطی مطرح می‌شوند عبارت‌اند از معادلات خطی، ماتریس‌ها و فضای برداری. به مثال‌های زیر توجه کنید تا بهتر متوجه شوید مفهوم و کاربرد جبر خطی چیست.

مثال ۱

یک نمونه سقف شیروانی را تصور کنید که اگر سه قدم زیر این سقف و روی زمین گام بردارید، این سقف به اندازه یک قدم از زمین فاصله می‌گیرد (شیب سقف $$\frac{1}{3}$$ است) و اگر شش قدم روی زمین به جلو حرکت کنید، انتظار دارید که سقف دو قدم از زمین فاصله بگیرد.

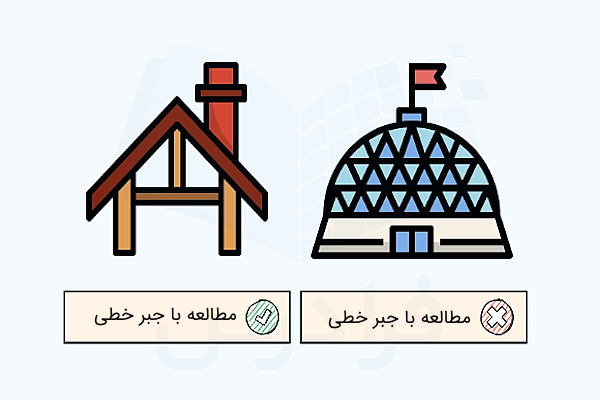
در مقابل، یک سقف گنبدی شکل را تصور کنید، به این صورت که با هر قدم روی سطح زمین، ارتفاع سقف از زمین به مقدار متفاوتی تغییر پیدا کند. در حالت اول توصیف و مطالعه ریاضیات مسئله به کمک جبر خطی امکان‌پذیر است، در حالی که در مورد سقف گنبدی شکل، جبر خطی به ما کمکی نمی‌کند.

مثال ۲

فرض کنید دستگاهی از معادلات شامل دو معادله‌ خطی با دو مجهول $$x_1$$ و $$x_2$$ به شکل زیر داده شده است:

$$\begin{cases}2x_1 + x_2 = 0 \\x_1 - x_2 = 1 \end{cases}$$

این دستگاه فقط یک جواب یکتا برای $$x_1$$ و $$x_2$$های عضو مجموعه اعداد حقیقی دارد که عبارت‌اند از:

$$x_1 = \frac{1}{3}$$

$$x_2 = - \frac{2}{3}$$

اما این جواب را می‌توان به روش‌های مختلفی به‌ دست آورد. یک روش این است که یکی از مجهولات را از یکی از معادلات جدا کنیم و در معادله‌ دیگر جایگذاری کنیم. برای مثال، از معادله‌ دوم داریم:

$$x_1 = 1 + x_2$$

با جایگذاری این مقدار در معادله‌ اول خواهیم داشت:

$$2(1+x_2) + x_2 =0$$

از این عبارت $$x_2 = - \frac{2}{3}$$ به دست می‌آید و در نتیجه برای متغیر دیگر نیز خواهیم داشت:

$$x_1 = \frac{1}{3}$$

روش دیگر این است که به شکلی منظم‌تر متغیرها را حذف کنیم. به‌ عنوان مثال، می‌توانیم دو برابر معادله‌ دوم را از معادله‌ اول کم کنیم تا متغیر $$x_2$$ محاسبه شود.

یادگیری جبر خطی با فرادرس

در این بخش پیشنهاد می‌کنیم برای اینکه بهتر متوجه شوید جبر خطی چیست، فیلم‌های آموزشی تهیه شده در مجموعه فرادرس را مشاهده کنید تا با بهره‌گیری از آموزش تصویری و حل سوالات متنوع به مفاهیم این درس کاملا مسلط شوید:

• فیلم آموزش رایگان جبر خطی چیست؟ + مفاهیم و کاربردها به زبان ساده فرادرس
• فیلم آموزش جبر خطی – جامع و با مفاهیم کلیدی فرادرس
• فیلم آموزش جبر خطی – مرور و حل مساله فرادرس

شاخه های جبر خطی چیست؟

پس از اینکه یاد گرفتید کلیات جبر خطی چیست، در این بخش شاخه‌‌های مختلف آن را معرفی می‌کنیم. جبر خطی را به عنوان شاخه‌ای از درس ریاضی معرفی می‌کنیم که در آن به مطالعه توابع خطی در فضای برداری پرداخته می‌شود. همچنین زمانی که بتوانیم اطلاعات مرتبط با توابع خطی را در یک آرایه منظم نمایش دهیم، می‌گوییم از نمایش ماتریسی استفاده کرده‌ایم.

به این ترتیب اگر بخواهیم به‌طور خلاصه بگوییم جبر خطی چیست، بهترین تعریف این است که جبر خطی را علم مطالعه فضای برداری، بردارها، توابع خطی، سیستم معادلات خطی و ماتریس‌ها در نظر بگیریم. پس از تسلط بر این مفاهیم می‌توان برای مباحث پیشرفته‌تری مانند هندسه مدرن و آنالیز تابعی آماده شد. برای جبر خطی بسته به سطح دشواری مباحث مطرح شده در آن، می‌توانیم سه شاخه مختلف را در نظر بگیریم که عبارت‌اند از:

• جبر خطی مقدماتی
• جبر خطی پیشرفته
• جبر خطی کاربردی

هر کدام از این موارد موضوعات مختلفی را پوشش می‌دهند و به جنبه‌ها یا سطوح مختلفی از مفهوم ماتریس‌، بردار و توابع خطی می‌پردازند. در این مطلب بیشتر تمرکز ما روی مباحث جبر خطی مقدماتی است.

جبر خطی مقدماتی چیست؟

یادگیری جبر خطی را بهتر است با جبر خطی مقدماتی شروع کنید. این شاخه شامل مباحثی مانند انواع عملیات ساده روی ماتریس‌ها، محاسبات موردنیاز برای سیستم‌‌های معادلات خطی و جنبه‌‌های خاصی از مفاهیم مربوط به بردارها است. در ادامه این بخش توضیح می‌دهیم مهم‌ترین تعاریف یا عناصر سازنده شاخه‌ مقدماتی از جبر خطی چیست.

جبر خطی به بررسی روابطی می‌پردازد که میان کمیت‌هایی برقرارند که می‌توان آن‌ها را جمع و یا در اعداد ضرب کرد، به گونه‌ای که این عملیات‌ از یک سری قواعد خطی تبعیت کنند. این قواعد خطی دو ویژگی زیر را دارند:

• هم‌افزایی (Additivity): به این معنا که اگر دو ورودی با هم جمع شوند، خروجی نیز برابر با جمع دو خروجی خواهد بود.

$$f(x) + f(y) = f(x+y)$$

• همگنی (Homogeneity): به این مفهوم که اگر ورودی در عددی ضرب شود، خروجی نیز به همان نسبت تغییر می‌کند.

$$cf(x) = f(cx)$$

اگر علاقه‌مند هستید مباحث جبر خطی را با حل مثال‌ها و تمرین‌های متنوع بیازموزید، می‌توانید فیلم آموزش جبر خطی – مرور و حل مساله فرادرس را مشاهده کنید که لینک آن نیز در ادامه برای شما قرار داده شده است:

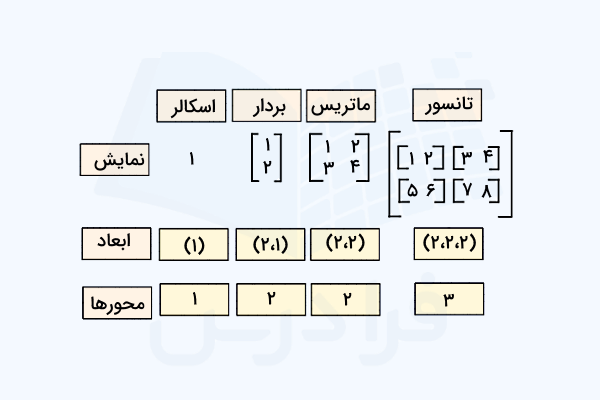
اسکالر

اسکالر به کمیتی گفته می‌شود که فقط اندازه دارد و جهتی برای آن تعریف نشده است. تعریف اسکالر در جبر خطی به ما کمک می‌کند تا بتوانیم فضای برداری را به درستی تعریف کنیم. در جبر خطی اسکالرها معمولا اعداد حقیقی هستند. همچنین باید دقت کنید اگر چه تعریف اسکالر در جبر خطی همان تعریف کمیت اسکالر در فیزیک است، اما مفهوم مهمی که در جبر خطی با دیدن اسکالر به ما منتقل می‌شود این است که با یک داده یا تک نقطه منفرد سروکار داریم که هیچ جهت یا بعد مشخصی ندارد.

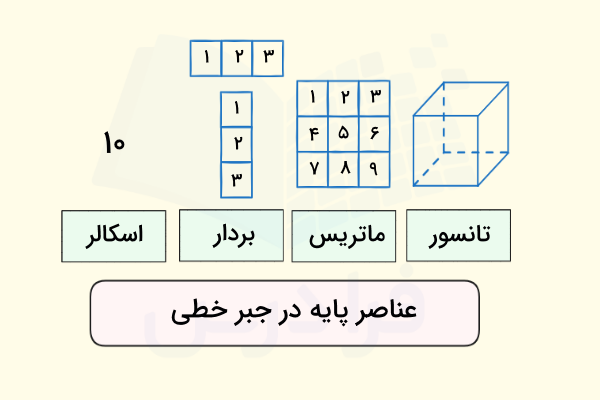
همچنین این تک نقطه یا داده منفرد امکان تقسیم شدن به اجزای دیگر را نیز ندارد. در بخش بعد و در کنار توضیح مفهوم بردار، بهتر می‌توان متوجه شد منظور از اسکالر در جبر خطی چیست. در تصویر بالا عدد $$10$$ یک اسکالر است و همان‌طور که ملاحظه می‌کنید، این عدد یک تک عدد یا تک داده است که هیچ بعدی ندارد. متغیرهایی که به اسکالرها نسبت داده می‌شوند عموما توسط حروف کوچک انگلیسی نمایش داده می‌شوند.

شیوه نمایش این متغیرها به این شکل است که معمولا همراه با فضایی که جزئی از آن هستند، نشان داده می‌شوند. برای مثال، اگر بخواهیم اسکالر $$a$$ را به شیوه درستی و مطابق با اصول جبر خطی نمایش دهیم، آن را به شکل $$a \in R$$ نشان می‌دهیم، به این معنا که اسکالر $$a$$ می‌تواند هر مقداری از مجموعه اعداد حقیقی یا $$R$$ را بپذیرد.

بردار

بردار در جبر خطی به عنوان یکی از عناصر فضای برداری تعریف می‌شود و کمیتی است که هم اندازه و هم جهت را در مورد هر عنصر یا عضو فضای برداری به ما نشان می‌دهد. در واقع اگر چند اسکالر داشته باشیم و بخواهیم به کمک آن‌ها جهت خاصی را در فضای برداری نشان دهیم، آن‌گاه یک بردار خواهیم داشت. بنابراین عناصر سازنده بردارها در جبر خطی، اسکالر‌ها هستند. بردارها در جبر خطی به دو گروه تقسیم می‌شوند:

• بردارهای ردیفی یا Row Vectors که به شکل افقی پر می‌شوند.
• بردارهای ستونی یا Column Vectors که به شکل عمودی پر می‌شوند.

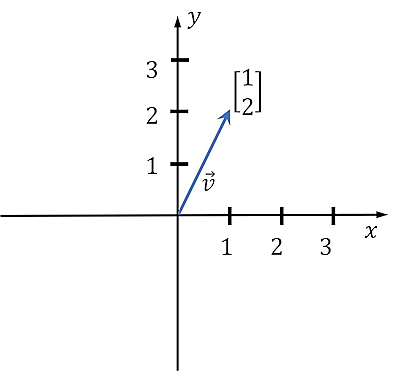
بردارها بر خلاف اسکالرها دارای بعد هستند. اما باید دقت کنیم که این عناصر در جبر خطی در مقایسه با ماتریس‌ها یک بعد دارند یا به عبارت دیگر تک بعدی محسوب می‌شوند. پس بردار در جبر خطی به شکل مجموعه یا آرایه‌ای از چند عدد یا اسکالر تعریف می‌شود. عموما برای نشان دادن بردارها و متمایز کردن آن‌ها از اسکالرها از حروف انگلیسی کوچک بولد شده به شکل $$x$$ استفاده می‌شود. ترتیب عناصری که در یک بردار قرار می‌گیرند، مهم است و به همین علت برای مثال، اولین عنصر یک بردار را با $$x_1$$ نشان می‌دهیم.

همان‌طور که گفتیم، این اجزا اسکالر هستند، پس $$x_1$$ یک اسکالر است و لازم نیست آن را به شکل بولد شده نمایش دهیم. از طرفی با توجه به اینکه بردار دارای بعد است، پس لازم است ابعاد و فضای عددی آن نیز مشخص شود. به همین منظور بردار $$x$$ در جبر خطی توسط $$<b>x</b> \in R^n$$ نشان داده می‌شود، به این معنا که تمام مقادیر $$x$$ حقیقی هستند و این بردار دارای $$n$$ عنصر اسکالر است. از بردار برای مشخص کردن موقعیت یک نقطه در فضا استفاده می‌شود. پس هر کدام از عناصر یا مولفه‌های بردار متناظراند با تصویر بردار روی یکی از محورهای دستگاه مختصات موردنظر.

همچنین در زمینه کار با بردارها بهتر است به مباحثی نظیر انواع بردار، ضرب داخلی، ضرب خارجی و جمع بردارها کاملا مسلط باشید. برای مثال، ضرب داخلی (ضرب نقطه‌ای) این امکان را برای شما فراهم می‌کند تا به اندازه‌گیری زاویه و طول یا نرم بردار در فضای برداری بپردازید. بنابراین اگر ضرب داخلی دو بردار برابر با صفر شود، زاویه بین آن‌ها قائمه است و می‌گوییم آن دو بردار عمود (متعامد) هستند.

فرض کنید دو بردار $$\vec {u}$$  و $$\vec {v}$$ را به شکل $$\vec {u} = (u_1, u_2, u_3)$$ و $$\vec {v} = (v_1, v_2, v_3)$$ دارید. مهم‌ترین فرمول‌‌های جبر خطی متناظر با این دو بردار عبارت‌اند از:

$$\vec {u} + \vec {v} = (u_1 + v_1 , u_2 + v_2 ,u_3 + v_3 )$$

$$\vec {u} - \vec {v} = (u_1 - v_1 , u_2 - v_2 ,u_3 - v_3 )$$

$$|| \vec {u} || = \sqrt{u_1^2 +u_2^2 +u_3^2 }$$

$$\vec {u} . \vec {v} = u_1 v_1 +u_2 v_2 + u_3 v_3$$

$$\vec {u} \times \vec {v} = (u_2 v_3 - u_3v_2, u_3 v_1 - u_1v_3, u_1 v_2 - u_2v_1)$$

فضای برداری

در بخش قبل یاد گرفتیم مفهوم بردار در جبر خطی چیست و دیدیم با اینکه از دید هندسی، بردار پاره‌خطی جهت‌دار و دارای طول و جهت است، اما از دید جبر خطی بردار به مجموعه‌ای مرتب از اعداد گفته می‌شود که دارای ارتباط خاصی با هم هستند. برای مثال، بردار $$\vec {v} = (3,2)$$ در فضای دو بعدی نشان‌ دهنده نقطه‌ای با مختصات $$(3,2)$$ با جهتی از مبدا به سمت این نقطه است.

بردارها را می‌توان با هم جمع کرد یا در عددی ضرب کرد و این دو نوع عملیات، پایه‌های فضای برداری را شکل می‌دهند. اگر $$V$$ را مجموعه‌ای از بردارها در نظر بگیریم که بتوان روی آن‌ها دو عمل جمع و ضرب اسکالر را انجام داد، به‌ گونه‌ای که قوانین خاصی مانند شرکت‌پذیری، وجود بردار صفر و ... همواره برقرار باشد، آنگاه $$V$$ یک فضای برداری نامیده می‌شود. در واقع فضای برداری توسط مجموعه‌ای از اجزا به نام بردارها تعریف می‌شود و این بردارها در چنین فضایی این قابلیت را دارند که با هم جمع شوند یا در هم ضرب شوند.

دقت کنید اگر $$V$$ فضای برداری روی میدان اعداد حقیقی یا $$R$$ باشد، در این صورت هر دو بردار $$u , v \in V$$ و هر عدد حقیقی مانند $$a$$ و $$b$$ لازم است از قوانین زیر پیروی کنند:

• جابجایی: $$u + v = v + u$$
• شرکت‌پذیری: $$w+ (u + v) = (w + v )+ u$$
• وجود بردار صفر یا $$0$$، طوری که $$0 + u = u$$
• وجود بردار قرینه یا $$-v$$، طوری که $$v + (-v) = 0$$
• $$v(ab) = a (vb)$$
• $$v = v.1$$
• $$bv + av = (a+b) v$$
• $$av + au = a (v+u)$$

این ویژگی‌های یک فضای برداری تضمین می‌کنند که می‌توانیم با بردارها دقیقا مانند اعداد رفتار کنیم، با این تفاوت که هر بردار ممکن است چند مولفه داشته باشد.

ماتریس

یک ماتریس شامل گروهی از بردارها است و در ساده‌ترین حالت خود از یک بردار افقی یا یک بردار عمودی ساخته می‌شود. بنابراین عناصر سازنده ماتریس‌ها در جبر خطی، بردارها هستند. ماتریس‌ها در حقیقیت یک آرایه دو بعدی از اعداد یا اسکالرها هستند. یک جدول را می‌توانیم به عنوان مثال ساده‌ای از یک ماتریس در نظر بگیریم. برای نمایش متمایز ماتریس از بردار، به‌جای حروف کوچک از حروف بزرگ انگلیسی و به شکل بولد شده استفاده می‌کنیم. برای مثال، $$X$$ نشان‌دهنده ماتریسی به نام $$X$$ است.

اگر ماتریسی شامل اعداد حقیقی قرار گرفته در $$m$$ ردیف و $$n$$ ستون باشد، آن را با $$<b>X</b> \in R^{mxn}$$ توصیف می‌کنیم. همچنین هر کدام از عناصری که در داخل یک ماتریس قرار می‌گیرند، به ترتیب بعد یا درایه نوشته می‌شوند. برای مثال، اولین عنصر یک ماتریس درایه $$X_{1,1}$$ است که در گوشه بالا سمت چپ قرار می‌گیرد، در حالی که آخرین عنصر یا درایه ماتریس به شکل $$X_{m,n}$$ تعریف می‌شود و متناظر است با گوشه سمت راست و پایین ماتریس.

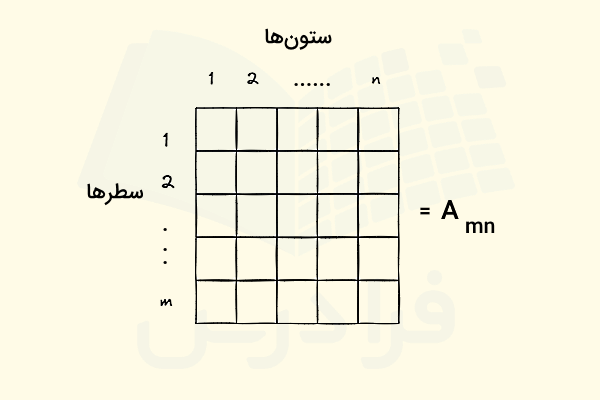
همچنین در زمینه کار با ماتریس‌ها بهتر است به موضوعاتی مانند اپراتورها یا عملگرهای ماتریسی، دترمینان، ترانهاده ماتریس و انواع ماتریس تسلط کافی داشته باشید. برای مثال، اگر دو ماتریس مربعی مانند $$A$$ و $$B$$ داشته باشیم که درایه‌های هر کدام به ترتیب معادل باشند با $$a_{ij}$$ و $$b_{ij}$$، آنگاه فرمول‌های مهم جبر خطی برای این دو ماتریس به شکل زیر خواهند بود:

$$A^{-1}A = 1$$

$$C = A + B , c_{ij} = a_{ij} + b_{ij}$$

$$C = A - B , c_{ij} = a_{ij} - b_{ij}$$

$$kA = ka_{ij}$$

$$C = AB =\sum _ {k=1}^n a_{ik}b{kj}$$

تانسور

تانسور به گروهی از ماتریس‌ها گفته می‌شود که یک فضای سه بعدی را تشکیل می‌دهند. پس تانسور آن جزئی از جبر خطی است که دارای سه بعد است و از کنار هم قرار گرفتن ماتریس‌ها ساخته می‌شود. یک مثال ملموس برای تانسور، مکعب روبیک است. هر کدام از عناصر تانسوری مانند تانسور $$A$$ را به شکل $$A_ {i,j,k}$$ نمایش می‌دهیم. تصویر زیر به عنوان یک جمع‌بندی نشان می‌دهد تفاوت‌ها در شیوه نمایش، ابعاد و محورهای بکار رفته در مورد هر یک از عناصر سازنده جبر خطی چیست:

معادلات خطی

معادلات خطی فرم استادنداری به شکل $$a_1x_1 + a_2x_2 + ... + a_nx_n$$ دارند. این معادلات یکی از پایه‌‌های اصلی جبر خطی را تشکیل می‌دهند. موضوعات زیر در حوزه بررسی معادلات خطی قرار می‌گیرند:

• معادلات خطی با یک متغیر
• معادلات خطی با دو متغیر
• معادلات خطی همزمان
• حل معادلات خطی
• راه‌حل‌های یک معادله خطی
• رسم معادلات خطی

با توجه به اینکه فرمول‌ها بخش مهمی از جبر خطی‌اند و به ما کمک می‌کنند تا محاسبات ساده‌تری داشته باشیم، مهم‌ترین فرمول‌های جبر خطی در زمینه معادلات خطی به شکل زیر فهرست می‌شوند:

• فرم کلی یک معادله خطی: $$ax + by = c$$
• فرم شیب و عرض از مبدا: $$y = mx + b$$
• $$a + b = b + a$$
• $$a + O = O + a = a$$

بر این اساس، دستگاه معادلات خطی نیز به مجموعه‌ای از چند معادله خطی گفته می‌شود که چند مجهول مشترک دارند. هدف از حل یک دستگاه معادلات خطی این است که مقادیری برای متغیرها پیدا کنیم که همزمان در تمام معادلات صادق باشند. همچنین دستگاه معادلات خطی را می‌توان به صورت یک ماتریس ضرایب به نام $$A$$، یک بردار شامل مقادیر مجهول و یک بردار شامل مقادیر ثابت نوشت:

$$b = A x$$

این شیوه نمایش به ما کمک می‌کند تا محاسبات عددی و تحلیلی ساده‌تری داشته باشیم.

روش های حل دستگاه معادلات خطی

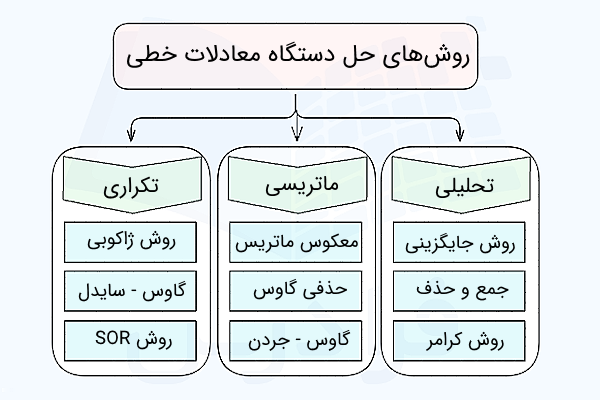
در این بخش به شکلی مختصر توضیح می‌دهیم که روش‌‌های حل دستگاه معادلات خطی در جبر خطی چیست. حل دستگاه معادلات خطی را می‌توان به سه روش کلی شامل روش‌های تحلیلی (دقیق)، روش‌های ماتریسی و روش‌های تکراری حل کرد. در ادامه هر کدام را توضیح می‌دهیم.

روش‌ های تحلیلی

روش‌های تحلیلی یا دقیق حل دستگاه معادلات خطی شامل سه روش زیر هستند:

• روش جایگزینی: یکی از معادلات برای یک متغیر حل می‌شود و سپس در معادلات دیگر جایگذاری می‌شود. این روش برای حل دستگاه‌ معادلات کوچک مناسب است.
• روش جمع و حذف: با جمع یا تفریق معادلات، برخی مجهولات حذف می‌شوند تا دستگاه ساده‌تر شود.
• روش کرامر: برای دستگاه‌های مربع و غیرتکین و با استفاده از دترمینان‌ها جواب‌ها محاسبه می‌شوند. این روش نیز برای حل دستگاه‌ معادلات کوچک مناسب است.

روش‌ های ماتریسی

در ادامه توضیح می‌دهیم روش‌های ماتریسی حل دستگاه معادلات خطی در جبر خطی چیست:

• روش معکوس ماتریس: اگر ماتریس ضرایب $$A$$ معکوس‌پذیر باشد، پاسخ برابر است با $$A^{-1}b = x$$. این روش محاسبات زیادی دارد و برای دستگاه‌ معادلات بزرگ توصیه نمی‌شود.
• روش حذفی گاوس: با انجام یک سری عملیات سطری، ماتریس ضرایب به فرم پلکانی تبدیل شده و مجهولات از آخر به اول به دست می‌آیند.
• روش گاوس – جردن: نسخه پیشرفته‌تری از روش حذفی گاوس است که با انجام عملیات سطری روی ماتریس الحاقی، آن را به فرم سطری، پلکانی و کاهش‌ یافته تبدیل می‌کند تا جواب‌ها مستقیما به دست آیند. فرم سطری پلکانی کاهش‌ یافته فرمی از ماتریس است که در آن هر سطر نسبت به سطر قبل با یک ستون جلوتر شروع می‌شود، عناصر محوری برابر با یک هستند و در هر ستون محوری، بقیه عناصر صفراند.

روش‌ های تکراری

در نهایت روش‌های تکراری را برای حل دستگاه معادلات خطی داریم که شامل موارد زیر هستند:

• روش ژاکوبی: در هر گام، هر مجهول بر اساس مقادیر قبلی تمام مجهولات بروزرسانی می‌شود. سرعت همگرایی این روش کند است.
• روش گاوس – سایدل: این روش مشابه روش ژاکوبی است، اما از مقادیر تازه محاسبه‌ شده بلافاصله استفاده می‌کند و سریع‌تر همگرا می‌شود.
• روش‌های پیشرفته‌تری مانند SOR و Conjugate Gradient: این روش‌ها در حل دستگاه معادلات بسیار بزرگ یا تنک (Sparse) و در مسائل عددی و مهندسی بکار می‌روند.

جبر خطی پیشرفته چیست؟

پس از اینکه یاد گرفتید اصول مقدماتی جبر خطی چیست، مفاهیم پیشرفته‌تر در زمینه معادلات خطی، بردارها و ماتریس‌ها در جبر خطی پیشرفته مطرح می‌شوند. در این مطلب از مجله فرادرس برخی از این مفاهیم مهم از جمله تبدیلات خطی، معکوس ماتریس، بردار ویژه و نگاشت خطی را معرفی می‌کنیم.

تبدیل خطی

در اولین بخش توضیح می‌دهیم معنای تبدیل خطی در جبر خطی چیست. تبدیل خطی به تبدیلی گفته می‌شود که در آن‌ یک تابع از یک فضای برداری به فضای برداری دیگری برده می‌شود. نکته مهم در این نوع تبدیلات این است که ساختار خطی هر فضای برداری نیز حفظ شده است.

معکوس یک ماتریس

اگر معکوس یک ماتریس را بدانیم، با ضرب آن در ماتریس اولیه یک ماتریس همانی به دست خواهیم آورد. پس اگر ماتریس اولیه ما $$A$$ و معکوس آن $$A^{-1}$$  باشد، داریم:

$$A^{-1} A = I$$

در این رابطه $$I$$ نماد ماتریس همانی است.

بردار ویژه

بردار ویژه یا Eigenvector برداری مخالف صفر است که با اعمال یک تبدیل خطی روی آن توسط فاکتور اسکالری به نام ویژه مقدار تغییر می‌کند.

نگاشت خطی

نگاشت خطی یا Linear Map به نگاشت یا تبدیلی گفته می‌شود که عملیات جمع یا ضرب برداری در آن حفظ شده است. در واقع در این تبدیل دو فضای برداری به هم مرتبط می‌شوند. در بخش‌ جبر خطی مقدماتی به دو خاصیت مهم هم‌افزایی و همگنی اشاره کردیم. در واقع تمام توابعی که این دو ویژگی‌ را داشته باشند، نگاشت‌ خطی‌اند. مطالعه نگاشت‌ها و ساختارهایی که روی داده‌ها اعمال می‌کنند، هسته اصلی جبر خطی را تشکیل می‌دهد.

جبر خطی کاربردی چیست؟

در این بخش می‌آموزید مهم‌ترین مباحث مطرح شده در شاخه کاربردی جبر خطی چیست. آشنایی با جبر خطی کاربردی عموما برای دانشجویان تحصیلات تکمیلی و در رشته‌هایی مانند ریاضیات کاربردی، مهندسی و فیزیک مناسب است. در این شاخه تلاش بر این است که مفاهیم ابتدایی و پیشرفته جبر خطی را با کاربردهای عملی آن‌ها پیوند دهیم. موضوعاتی مانند نرم یک بردار، تجزیه QR، مکمل شور یک ماتریس و ... در این حوزه قرار می‌گیرند.

کاربردهای جبر خطی چیست؟

در بخش‌های قبل یاد گرفتیم که مهم‌ترین مفاهیم و اصول در جبر خطی چیست. در این بخش به برخی از کابردهای عملی جبر خطی اشاره می‌کنیم. اغلب الگوریتم‌های ساده با استفاده از مفاهیم پایه در جبر خطی یعنی ماتریس‌ها توسعه پیدا کرده‌اند.

در واقع جبر خطی همان صفحه گسترده‌های کوچکی را در اختیار شما قرار می‌دهد که برای حل و بررسی معادلات ریاضی لازم دارید، به این ترتیب که می‌توان با استفاده از جدول داده‌ها (ماتریس) به ایجاد جداول به‌روزرسانی شده‌‌ای از جداول اولیه پرداخت. در حقیقت این قدرت چنین صفحات گسترده‌ای است که به صورت یک یا چند معادله نوشته می‌شوند. بیشترین کاربردهای جبر خطی را می‌توان در موضوعات زیر خلاصه کرد:

• پردازش سیگنال
• برنامه‌نویسی
• علم داده و علوم کامپیوتر
• توسعه الگوریتم‌ها

پردازش سیگنال

از جبر خطی و محاسبات آن در دستکاری و کدگذاری سیگنال‌هایی مانند سیگنال‌های رادیویی یا ویدئویی استفاده می‌شود. همچنین از فرمول‌های این شاخه از ریاضیات می‌توان در پردازش و تحلیل چنین سیگنال‌‌هایی استفاده کرد.

برنامه‌ نویسی خطی

برنامه‌نویسی خطی یکی از تکنیک‌های بهینه است که با هدف تعیین بهترین خروجی توابع خطی بکار می‌رود.

علوم کامپیوتر و علم داده

دانمشندان داده با کاربرد الگوریتم‌‌های جبر خطی می‌توانند مسائل پیچیده را حل کنند. جهت کسب اطلاعات بیشتر در این زمینه، می‌توانید مطلب «کاربرد جبر خطی در علم داده‌ها و یادگیری ماشین – بخش اول» از مجله فرادرس را مطالعه کنید.

الگوریتم های پیش گویانه

الگوریتم‌های پیش‌گویانه از مدل‌های خطی توسعه داده شده توسط مفاهیم جبر خطی استفاده می‌کنند.