جبر خطی – بررسی کاربردهای عملی در پیش‌بینی هزینه‌های مسیر

در این نوشته به بررسی کاربرد عملی جبر خطی در زمینه پیش‌بینی هزینه‌های مسیر می‌پردازیم. این مسئله از یک مشکل در مسیریابی اوبر الهام گرفته است. تصور کنید شما خدمات نقشه گوگل هستید و مشتری شما می‌خواهد بداند که بهترین مسیر از نقطه الف به نقطه ب کدام است. اگر نقشه شهر را داشته باشید، پاسخ این سؤال آسان به نظر می‌رسد. کافی است از الگوریتم دیکسترا (Dijkstra) برای یافتن کوتاه‌ترین مسیر استفاده کنید و پاسخ را به کاربر عرضه نمایید. اما شاید ما اشتباه می‌کنیم.

تاکسی‌های آنلاین

اگر تاکنون از سرویس‌های تاکسی آنلاین مانند اوبر استفاده کرده باشید، می‌دانید که برخی اوقات کوتاه‌ترین مسیر، آن مسیری است که آسفالت مناسبی ندارد و یا حجم ترافیک آن بالا است. اگر در شهری زندگی می‌کنید که جای‌جای آن نشانه‌هایی از فقر و جرم مشاهده می‌شود، مسلماً مسیرهایی وجود دارند که به هر قیمتی می‌خواهید از آن‌ها اجتناب کنید. چند عامل محیطی وجود دارند که بسته به وضعیت آب‌وهوا، زمان روز و موقعیت مسیر می‌توانند بر مدت سفر تأثیر بگذارند. بنابراین عواملی پیچیده‌تر از صرفاً فاصله جغرافیایی می‌توانند بر این مسیریابی تأثیر بگذارند و این ملاحظات در هنگام جستجو برای مسیر بهینه حائز اهمیت است.

نرم‌افزار ویز (Waze) این برنامه‌ریزی را به طور هوشمندانه‌ای انجام می‌دهد. Waze از نشانگرهای اضافی مانند تصادف‌ها، دوربین‌های پلیس راهنمایی و چاله‌های خیابان‌ها نیز پشتیبانی می‌کند. این برنامه از GPS کاربر برای تخمین سرعت استفاده کرده و از آن برای محاسبه شدت ترافیک بهره می‌گیرد. به همین دلیل است که رانندگان اوبر و تاکسی‌های معمولی در شهرهای شلوغ به استفاده از این برنامه علاقه‌مند هستند. اما مشخص شده است که این اپلیکیشن در اکثر موارد مسیرهای با کیفیت پایین یا موقعیت‌های خطرناک را صرفاً به خاطر اندکی سریع‌تر بودن پیشنهاد می‌دهد.

راهکار چیست؟

این وضعیت را چگونه می‌توان بهتر ساخت؟ به نظر می‌رسد که مدت سفر تنها متغیری نیست که باید در الگوریتم تصمیم استفاده کرد. ما می‌توانیم به طور مصنوعی متغیرها و نشانگرهای دیگری را وارد الگوریتم کرده و وزن نسبی آن‌ها را بسته به اهمیتشان تعیین کنیم؛ اما در نهایت امکان تعمیم آن به شهرها و افراد مختلف که اولویت‌های متفاوتی دارند وجود ندارد. به نظر می‌رسد که محاسبه تابع هزینه به طور ضمنی از بازخوردهای ساده کاربر گزینه‌ای پایدارتر، مقیاس‌پذیرتر و بهتر است. اگر بتوانیم پاسخی قطعی ارائه کنیم، می‌توانیم آن را به گوگل بفروشیم؛ اما مشخص شده است که باید به دنبال رویکردی ساده و کاملاً آمورشی باشیم. این پاسخ تنها شامل اندکی کاربرد جبر خطی است.

بیان مسئله

فرض کنید همه اطلاعاتی که دارید یک نقشه، یک سری مسیرها در آن و طول آن‌ها (به طور کلی هزینه) است. هدف شما این است که مقادیری به هر قطعه از مسیر انتساب دهید، به طوری که بتوانید به سادگی هزینه یک مسیر جدید را با جمع زدن هزینه قطعه‌های مختلف آن محاسبه کنید. اگر نقشه را به صورت یک گراف جهت‌دار (برخی مسیرها تنها یک طرفه هستند) و هر تقاطع، ادغام یا انشعاب را به صورت یک رأس گراف نشان دهیم، در این صورت یال‌های گراف تبدیل به واحدهای قطعه‌ای خواهند شد و هر مسیر به سادگی یک توالی مرتب از رئوس بازدید شده (یا به طور جایگزین یال‌های پیمایش شده) است.

برای این که تعریف فوق را به طور رسمی‌تری بیان کنیم، فرض کنید که یک گراف وزن‌دار به صورت (G = (V, E دارید که به تابع ناشناس ⁺w(e) : e ∊ E ⇾ ℝ مرتبط است و همچنین مجموعه‌ای از چندتایی‌های (pᵤ =({eᵥ}ᵤ, cᵤ وجود دارند که eᵥ ∊ E و ⁺cᵤ ∊ ℝ. هدف آن است که (W(e را بازسازی کنیم. اگر هر (w(e_v را به صورت w_v شمارش کنیم، می‌توانیم از مسیرهای {p_u} سیستمی از معادلات را به صورت زیر استخراج نماییم:

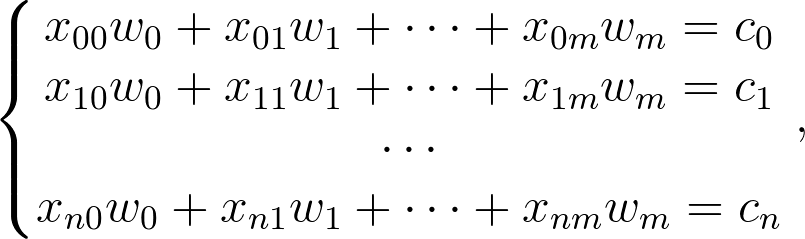
که در آن Xuv به صورت زیر تعریف شده است:

اگر دوست داشته باشید می‌توانید آن را به صورت Xw=c بازنویسی کنید. تا زمانی که rank(X) = m باشد می‌دانیم که دقیقاً چگونه می‌توانیم آن را حل کنیم. اگر چنین نباشد باز می‌توانیم تقریبی از پاسخ داشته باشیم. این وضعیت تا زمانی که c دقیق باشد، راه‌حلی معقول برای مسئله ما محسوب می‌شود؛ اما این حالت در زندگی واقعی بسیار نامحتمل است.

برای داشتن مدلی واقع‌گرایانه‌تر می‌توانیم تصور کنیم که معیارهای داخل مسیر ما در مورد c از سوی یک نویز تصادفی مانند (cᵤ ∼?(μᵤ, σᵤ آشفته می‌شوند. در این وضعیت پیش‌بینی رتبه کافی نیست و احتمالاً تنها تقریبی از راه‌حل را با کمینه‌سازی خطای ‖Xw-c‖ به دست می‌آوریم.

بررسی یک مثال

استفاده از مثال همیشه به یافتن راه‌حل بهتر کمک می‌کند. فرض کنید در یک شرکت مشاور در خصوص کلان‌داده که «Large Data» نام دارد، فعالیت می‌کنید و شهردار خوشحال شهر آرام زیزگی (Zizgy) مشتری شما است. ساکنان این شهر همگی یک نقشه دارند که شهردار خوشحال این شهر هر ماه از هلیکوپتر خود بر فراز شهر پخش می‌کند. مردم همواره از شلوغی شکایت دارند؛ اما لبخند رمزآمیز شهردار همواره باعث عقب‌نشینی آن‌ها می‌شود و همیشه او را می‌بخشند.

برای مدتی همه چیز در شهر زیزگی بر سبیل آرامش بود تا این که اوبر وارد شهر شده و ادعا کرد که نقشه شهر ناکامل است و رانندگانش نمی‌توانند کوتاه‌ترین مسیر را پیدا کنند و این مسئله باعث نارضایتی مشتریانش می‌شود. شهردار هرگز تا آن لحظه در مورد اندازه‌گیری طول مسیرها فکر نکرده بود و وقتی برای این مسئله اقدام کرد، متوجه شد خط‌کشی که دارد، حتی برای اندازه‌گیری کوتاه‌ترین مسیرها نیز کفایت نمی‌کند. خوشبختانه اوبر داده‌های خود را در اختیار شهردار قرار داد. این داده‌ها به صورت شواهدی از میزان علاقه رانندگان مختلف در انتخاب مسیر بین دو نقطه بود. بنابراین به طور طبیعی وی به کارشناسان شرکت شما مراجعه می‌کند تا از آن داده‌ها که بزرگ تصور می‌کرد، استفاده کند.

این داده‌ها شامل اطلاعات کاملی از مسیر انتخاب شده برای هر سفر و همچنین هزینه کلی بوده است. از آنجا که سیاست انتخاب مسیر کاملاً تعریف شده و در دسترس عموم وجود داشت، شما می‌توانید مسافت کلی پیمایش شده را از روی هزینه تخمین بزنید. همچنین از آنجا که شبکه مسیرها را می‌توان به صورت یک گراف نمایش داد، در می‌یابید که این مشکل در واقع یک مسئله کشف وزن یال است!

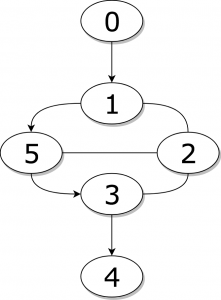
بعد از این که گراف مسیر به صورت تصویر فوق ایجاد شد، مسیرهای کد شده به صورت زیر در می‌آیند:

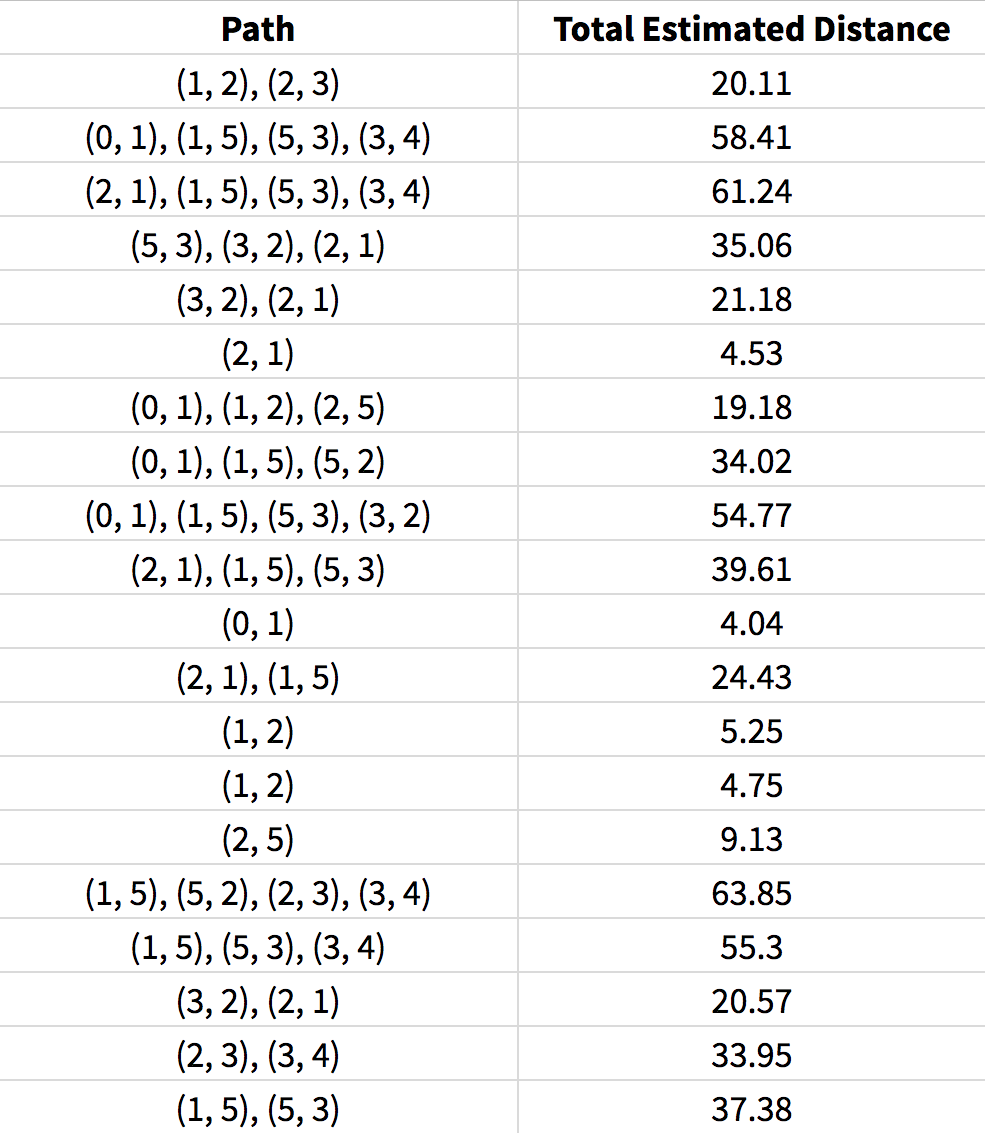
اگر به ترتیب الفبا بیان کنیم:

(0,1)=e₀, (1,2)=e₁, (1,5)=e₂, (2,1)=e₃

و همین طور تا آخر، در این صورت ماتریس نشانگر X به صورت زیر خواهد بود:

با استفاده از X و c می‌توانیم w را با روش کمترین مربعات تقریب بزنیم:

باقیمانده‌های Xw-b انحراف معیاری در حدود 0.65 دارند که معقول به نظر می‌رسد. یعنی این مقادیر به اندازه کافی متمایز هستند که برای یافتن کوتاه‌ترین مسیر مفید باشند. این نتیجه به شهردار ارائه می‌شود و وی در جلسه با لبخندی رضایت خود را اعلام می‌دارد.

فیلم آموزش ماتریس ها و جبر خطی – حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

با این حال وقتی شهردار نقشه شهر را با تقریب‌های مسافت به‌روزرسانی می‌کند، منشی‌اش به وی اعلام می‌کند که اندازه‌های واقعی را در نسخه‌ای قدیمی از نقشه شهر که شهردار قبلی تهیه کرده یافته است. مردم شهر وقتی می‌فهمند که شهردار بودجه شهر را صرف قرارداد مشاوره غیر لازمی کرده است ناراحت می‌شوند؛ اما وقتی شهردار نقشه‌ها را در سطح شهر پخش می‌کند از دیدن لبخند همیشگی وی ناراحتی‌شان را فراموش می‌کنند. آن خوشی خوش است که پایانش خوش باشد!

همان طور که مشخص شد، تخمین‌های ما به طور میانگین اختلافی در حد 0.53 واحد داشته است. گرچه برای مسیر 0 تا 1 خطایی به میزان 1.33 وجود دارد. توجه داشته باشید که در این مثال می‌توانستیم تخمین‌های خود را با بهره‌گیری از این واقعیت که مسیرهای دوطرفه مانند 2 به 5 متقارن هستند و فاصله از 2 تا 5 برابر با مسافت 5 تا 2 است، بهبود بخشیم. این دو مسیر عمداً جدا در نظر گرفته شده‌اند تا چارچوبی کلی‌تر به نمایش درآید که تحت این چارچوب بتوانیم برخی معیارهای هزینه‌ای تجریدی را تقریب بزنیم که به جهت مسیر نیز وابسته هستند (برای مثال حجم ترافیک در یک جهت می‌تواند سنگین‌تر از طرف دیگر باشد).

در صورتی که کنجکاو هستید این نتایج از کجا ناشی می‌شود باید بگوییم که داده‌های سفر از طریق انتخاب یک مسیر تصادفی در گراف و محاسبه مسافت کلی با افزودن نویز (ε∼?(0, 1 به دست آمده است. با داشتن داده‌های کافی می‌توانیم توزیع خطا را حدس بزنیم و توانایی انتخاب یک رویکرد بیزی برای بهبود دادن تخمین‌های مسافت را خواهیم داشت.

کدنویسی یک شبیه‌سازی

اینک که یک مثال را بررسی کردیم، احتمالاً جالب خواهد بود که پیاده‌سازی این چارچوب مدل را با استفاده از تنسورفلو (TensorFlow) مشاهده کنیم. دلیل این که تنسورفلو را انتخاب کردیم آن است که می‌خواهیم نشان دهیم این پلتفرم برای مقاصد یادگیری ماشین عمومی به جز یادگیری عمیق نیز تا چه حد می‌تواند مفید باشد.

فیلم آموزش جبر خطی با متلب در فرادرس

کلیک کنید

این انتخاب همچنین باعث می‌شود که بتوانیم یادگیری آنلاینی داشته باشیم که در آن داده‌های جدید به تدریج تولید می‌شوند و یادگیری بر مبنای آن‌ها صورت می‌گیرد. این حالت تا حدود زیادی نماینده یک پیاده‌سازی دنیای واقعی آماده کاربرد عملی است. در ابتدا کدی که برای تولید مسیرهای منفرد تصادفی از یک ماتریس مجاورت استفاده می‌کنیم را ارائه کرده‌ایم:

import numpy as np

def walk(adj, alpha=0, sigma=0):

    # Recursively visit neighbors until target is reached
    # or until all vertices are exhausted.
    def recurse(u, t, visited, neighbors):
        for v in np.random.permutation(neighbors):
            if v == t:
                return [v], adj[u, v]
            if v not in visited or (v in visited and np.random.sample() < alpha):
                vn = np.argwhere(adj[v] > 0).flatten()
                verts, dist = recurse(v, t, {*visited, v}, vn)
                if verts:
                    return [v, *verts], adj[u, v] + dist
            return [], 0

        # Pick some starting vertex
        start = np.random.randint(0, len(adj))
        # Ensure starting vertex has at least one neighbor
        while sum(adj[start] > 0) == 0:
            start = np.random.randint(0, len(adj))

        # Pick the target vertex
        target = np.random.randint(0, len(adj))
        # Ensure the path has at least one edge
        while target == start:
            target = np.random.randint(0, len(adj))

        # Build path recursively
        un = np.argwhere(adj[start] > 0).flatten()
        verts, dist = recurse(start, target, {start}, un)

        # Return hit matrix and total distance
        hits = np.zeros_like(adj, dtype=np.int32)

        if not verts:
            return hits, 0
        else:
            for u, v in zip([start, *verts], verts):
                hits[u, v] += 1
            return hits, dist + np.random.normal(scale=sigma)

در تصویر زیر نمونه‌ای از ماتریس مجاورتی را می‌بینید که کد ما انتظار دارد دریافت کند:

در این قالب هر عنصر غیر صفر نشان‌دهنده یک یال و مقدار آن نماینده وزن یال است. پارامتر سیگما (σ) انحراف معیار نویز اضافه شده به مسافت کلی را کنترل می‌کند و آلفا (α) احتمال بازدید مجدد از یک رأس را تعیین می‌کند. این پارامتر اخیر بدین منظور به مدل اضافه شده است تا مواردی که راننده‌ای اشتباه کرده و یک حلقه در مسیر خود ایجاد می‌کند را نشان دهد. اگر α = 0 باشد، X همچنان است که قبلاً تعریف کردیم، یعنی ماتریس نشانگر که نشان می‌دهد کدام رئوس در هر سفر بازدید شده‌اند. اگر α > 0 باشد در این صورت X تعداد دفعات بازدید از هر رأس را نمایش می‌دهد. در هر صورت معادله Xw=c تغییری نمی‌یابد و روش حل ما نیز همچنان یکسان است. فقط باید مطمئن شوید که α < 0.5 چون در غیر این صورت الگوریتم به دلیل بررسی مسیرهای چرخه‌ای زیاد، به احتمال زیاد موجب سرریز بافر می‌شود.

نکته‌ای که باید در نظر داشت این است که چون معادله حل‌کننده ما لزوماً از پیش نمی‌داند که کدام یال در گراف وجود دارد، ماتریس X را به صورت V|×|V|× n tensor x | کدگذاری می‌کنیم، که توانایی مدل‌سازی حتی گراف‌های جهت‌دار متراکم دارای حلقه را نیز دارد (توجه کنید که این وضعیت با توجه به تفسیر ما از یک نقشه معنی‌دار است) راه‌حل ما برای w در عمل همان ماتریس مجاورت است. در این ساختار معادله مسئله در واقع به صورت x:w=c است که عملگر دو نقطه (:) نشان‌دهنده فشردگی مضاعف تنسور است؛ اما این وضعیت دقیقاً همانند آن است که X را به صورت یک ماتریس V|²× n| نشان دهیم که ردیف‌های آن به صورت ماتریس‌های مسطح شده از تابع ()walk هستند. ادامه کد چنین است:

import tensorflow as tf

def make_dataset(adj, alpha=0, sigma=0):
    def path_gen():
        while True: # generate non-empty paths forever
            hits, dist = walk(adj, alpha, sigma)
            if np.any(hits):
                yield hits, dist
    return tf.data.Dataset.from_generator(
        path_gen,
        (tf.int32, tf.float32),
        (tf.TensorShape(adj.shape), tf.TensorShape([]))
    )

adj = np.array([
    [0, 5, 0, 0, 0, 0],
    [0, 0, 5, 0, 0, 20],
    [0, 5, 0, 15, 0, 10],
    [0, 0, 15, 0, 20, 0],
    [0, 0, 0, 0, 0, 0],
    [0, 0, 10, 15, 0, 0]
])

ds = make_dataset(adj, alpha=0.4, sigma=5)

sess = tf.Session()

with tf.name_scope("data"):
    iterator = ds.prefetch(1024).batch(1).make_one_shot_iterator()
    hits, dist = iterator.get_next()

with tf.name_scope("model"):
    weights = tf.get_variable("weights", adj.shape, initializer=tf.zeros_initializer)
    est_dist = tf.tensordot(tf.cast(hits, tf.float32), weights, 2)
    loss = tf.losses.mean_squared_error(dist, est_dist)

with tf.name_scope("train"):
    train_op = tf.train.GradientDescentOptimizer(1e-2).minimize(loss, global_step=tf.train.get_global_step())

sess.run(tf.global_variables_initializer())

for i in range(5000):
    sess.run(train_op)

این کد یک شیء مجموعه داده ایجاد می‌کند (که مسیرهای تصادفی را به صورت خلق‌الساعه تولید می‌کند)، ماتریس مجاورت را تعریف می‌کند، گراف محاسبه را تعریف کرده و در حدود 5000 تکرار تمرینی را اجرا می‌کند (در هر تکرار از یک مسیر منفرد استفاده می‌کند). وزن‌های نهایی که با استفاده از کد فوق به دست می‌آیند به صورت زیر است:

خطای میانگین مربعات (نسبت به وزن‌های واقعی) در حدود 0.85 است. این نتیجه به خصوص با توجه به این که 5000 مسیر داده‌های زیادی برای چنین گراف کوچکی محسوب می‌شوند، چندان خوب نیست. از آن جا که به مسیرها همواره یک مقدار نویز اضافه می‌شود، وزن‌ها هرگز در عمل به یک مقدار ثابت همگرا نمی‌شوند، بلکه نوسان می‌کنند.

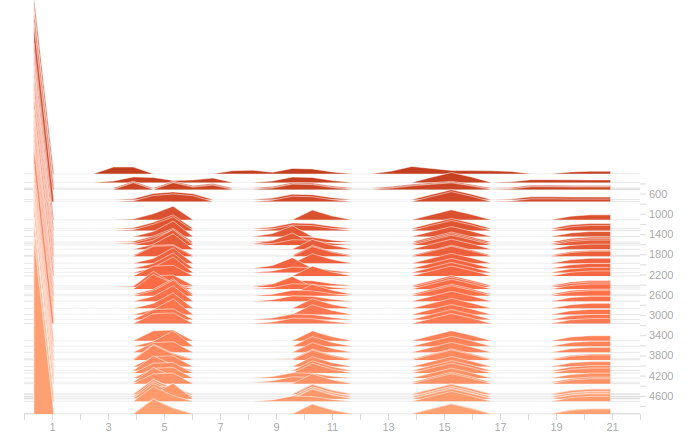
اگر نویزی در داده‌ها وجود نداشته باشد، وزن‌ها دقیقاً به راه‌حل دقیق همگرا خواهند بود.

می‌توانیم از نوسان‌های وزن برای تخمین توزیع احتمال بر روی این مقادیر استفاده کنیم:

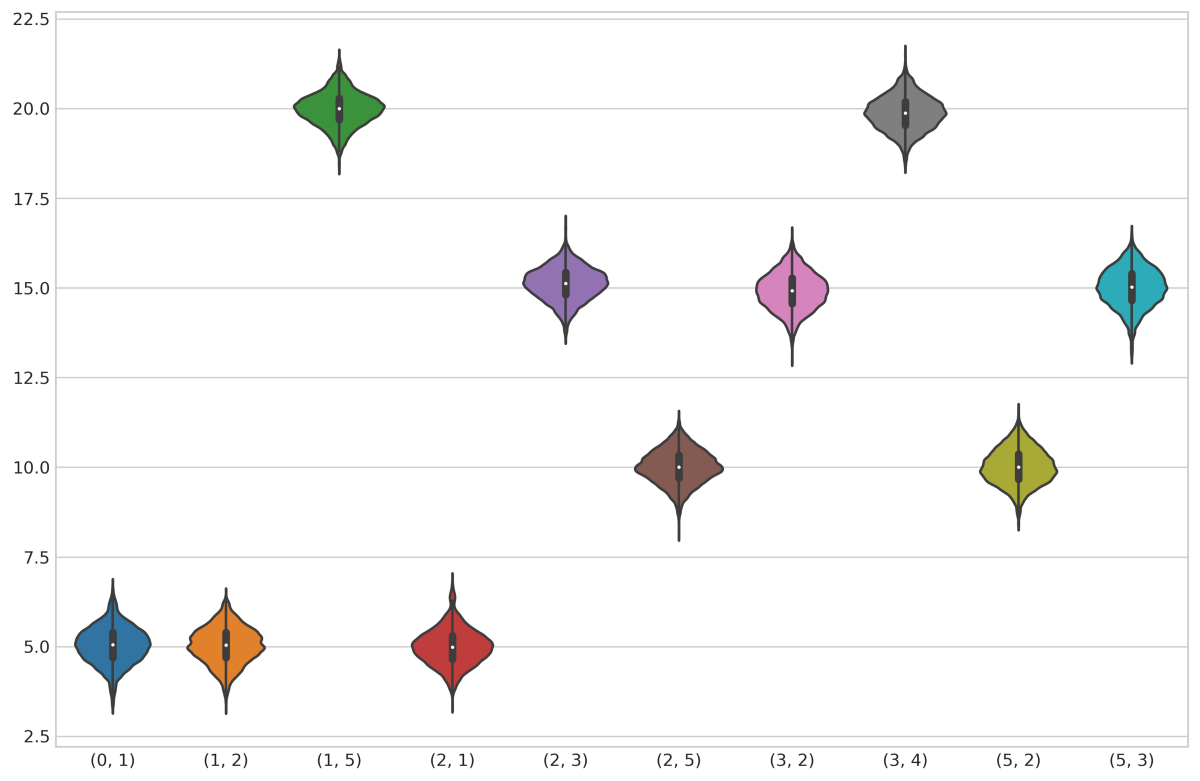
با محاسبه میانگین وزن‌ها بر روی حجم بالایی از تکرارها (یعنی 50،000) می‌توانیم تخمینی بهتر از مقادیر واقعی داشته باشیم:

به علاوه این دسته‌بندی باعث کاهش واریانس می‌شود.

با ترکیب هر دو تکنیک می‌توانیم تا حد امکان به مقادیر واقعی نزدیک شویم. همچنین می‌توانیم از نمونه‌ها برای ذخیره داده‌های تمرینی و احتمالاً یادگیری سریع‌تر بهره بگیریم. توجه داشته باشید که اگر وزن‌های واقعی در طی زمان ثابت نباشند، می‌توانیم داده‌های تمرینی و میانگین‌های وزنی را به یک پنجره اخیر مقید سازیم. در غیر این صورت هر چه داده‌ها را بیشتر تجمیع کنیم، بهتر خواهد بود. برای مشاهده کد کامل می‌توانید از این صفحه استفاده کنید.

سخن پایانی

پس از همه این مباحث بهتر است یک گام به عقب برداریم و تصویری کلی از آنچه انجام دادیم به دست آوریم. در این نوشته مثالی ارائه کردیم که در آن هدفمان تخمین مسافت‌های مسیرها بوده است به طوری که بتوان کوتاه‌ترین مسیر دلخواه را به دست آورد؛ اما در واقعیت مسافت‌های مسیر غالباً با دقتی کافی مشخص هستند و بهترین معیار برای کمینه‌سازی هزینه نیستند. پیشنهاد ما این بوده است که تنها از فاصله یا مدت سفر برای بهینه‌سازی استفاده نکنیم؛ بلکه از یک تابع هزینه ضمنی بهره بگیریم که به محیط و کاربر نیز بستگی دارد.

انتظار می‌رود این تابع همبستگی بالایی با مدت سفر داشته باشد؛ اما همچنین می‌تواند به عواملی که نمی‌توان همواره به طور مستقیم اندازه‌گیری نیز بستگی دارد. این عوامل می‌توانند شامل شرایط مسیر، موانع موقتی و همسایگی باشند. فرض کنید از کاربر می‌خواهیم که به هر سفر مستقل از راننده، امتیازی از 1 تا 5 بدهد. این امتیاز می‌تواند برای محاسبه یک نمونه هزینه ضمنی مورد استفاده قرار گیرد.

چند روش برای تخمین هزینه‌های آتی از این بازخورد وجود دارد؛ اما شاید ساده‌ترین روش این است که فرض کنیم برای هر کاربر هزینه یک تابع ثابت از خود مسیر به تنهایی است و وزن‌ها را به هر قطعه از مسیر انتساب دهیم. حتی اگر این وزن‌ها در طی زمان ثابت نباشند، رویکرد یادگیری آنلاین ما می‌تواند بر این اساس سازگار شود. در کمترین حالت، این نقطه شروعی برای رویکردهای پیچیده‌تر بسته به شرایط مختلف است.

اگر این نوشته مورد توجه شما واقع شده است، موارد زیر نیز احتمالاً برای شما جذاب خواهند بود:

• آموزش جبر خطی
• کاربرد جبر خطی در یادگیری عمیق
• یادگیری ماشین و بازشناسی الگو
• آموزش های رایگان ریاضی و فیزیک
• کاربرد جبر خطی در علم داده‌ها و یادگیری ماشین
• آموزش‌های ریاضیات

==