در آموزش‌های قبلی مجله فرادرس ، با روش ژاکوبی برای حل دستگاه معادلات خطی به فرم A x = b Ax = b A x = b A A A n × n n \times n n × n
روش گوس سایدل
ابتدا روش گوس سایدل را با جزئیات برای معادله‌ها بیان می‌کنیم، سپس فرم ماتریسی آن را ارائه خواهیم کرد.
فرض کنید x ( 0 ) = [ x 1 ( 0 ) x 2 ( 0 ) ⋮ x n ( 0 ) ] x ^ { ( 0 ) } =\begin {bmatrix} x _ 1 ^ { ( 0 ) } \\ x _ 2 ^ { ( 0 ) } \\ \vdots\\ x _ n ^ { ( 0 ) } \end {bmatrix} x ( 0 ) = x 1 ( 0 ) x 2 ( 0 ) ⋮ x n ( 0 ) x x x n n n n n n
E ( 1 ) : a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 E ( 2 ) : a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ E ( n ) : a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n = b n \large \begin {align} \quad \begin {matrix} E ( 1 ) : & a _ { 1 1 } x _ 1 & + & a _ { 1 2 } x _ 2 & + & \cdots & + & a _ { 1 n } x _ n & = & b _ 1 \\ E ( 2 ) : & a _ { 2 1 } x _ 1 & + & a _ { 2 2 } x _ 2 & + & \cdots & + & a _ { 2 n } x _ n & = & b _ 2 \\ \vdots & \vdots & & \vdots & & \ddots & & \vdots & & \vdots \\ E ( n ) : & a _ { n 1 } x _ 1 & + & a _ { n 2 } x _ 2 & + & \cdots & + & a _ { n n } x _ n & = & b _ n & \end {matrix} \end {align} E ( 1 ) : E ( 2 ) : ⋮ E ( n ) : a 11 x 1 a 21 x 1 ⋮ a n 1 x 1 + + + a 12 x 2 a 22 x 2 ⋮ a n 2 x 2 + + + ⋯ ⋯ ⋱ ⋯ + + + a 1 n x n a 2 n x n ⋮ a nn x n = = = b 1 b 2 ⋮ b n
ابتدا متغیر x i x _ i x i i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n E ( i ) E ( i ) E ( i )
x 1 = b 1 − [ a 12 x 2 + a 13 x 3 + . . . + a 1 n x n ] a 11 x 2 = b 2 − [ a 21 x 1 + a 23 x 3 + . . . + a 2 n x n ] a 22 ⋮ x n = b n − [ a n 1 x 1 + a n 2 x 2 + . . . + a n , n − 1 x n − 1 ] a n n \large \begin {align} \quad x _ 1 = \frac { b _ 1 - \left [ a _ { 1 2 } x _ 2 + a _ { 1 3 } x _ 3 + ... + a _ { 1 n } x _ n \right ] } { a _ { 1 1 } } \\ x _ 2 = \frac { b _ 2 - \left [ a _ { 2 1 } x _ 1 + a _ { 2 3 } x _ 3 + ... + a _ { 2 n } x _ n \right ] } { a _ { 2 2 } } \\ \quad \quad \quad \quad \quad \quad \vdots \quad \quad \quad \quad \quad \quad \\ x _ n = \frac { b _ n - \left [ a _ { n 1 } x _ 1 + a _ { n 2 } x _ 2 + ... + a _ { n , n - 1 } x _ { n - 1 } \right ] } { a _ { n n } } \end {align} x 1 = a 11 b 1 − [ a 12 x 2 + a 13 x 3 + ... + a 1 n x n ] x 2 = a 22 b 2 − [ a 21 x 1 + a 23 x 3 + ... + a 2 n x n ] ⋮ x n = a nn b n − [ a n 1 x 1 + a n 2 x 2 + ... + a n , n − 1 x n − 1 ]
اکنون تقریب نخست x ( 1 ) x^{(1)} x ( 1 ) x x x x 1 ( 1 ) x_1^{(1)} x 1 ( 1 ) x ( 0 ) x^{(0)} x ( 0 ) x 2 ( 1 ) x_2^{(1)} x 2 ( 1 ) x 1 ( 1 ) x_1^{(1)} x 1 ( 1 )
x 1 ( 1 ) = b 1 − [ a 12 x 2 ( 0 ) + a 13 x 3 ( 0 ) + a 14 x 4 ( 0 ) + . . . + a 1 n x n ( 0 ) ] a 11 x 2 ( 1 ) = b 2 − [ a 21 x 1 ( 1 ) + a 23 x 3 ( 0 ) + a 24 x 4 ( 0 ) + . . . + a 2 n x n ( 0 ) ] a 22 x 3 ( 1 ) = b 3 − [ a 31 x 1 ( 1 ) + a 32 x 2 ( 1 ) + a 34 x 4 ( 0 ) + . . . + a 3 n x n ( 0 ) ] a 33 ⋮ x n ( 1 ) = b n − [ a n 1 x 1 ( 1 ) + a n 2 x 2 ( 1 ) + a n 3 x 3 ( 1 ) + . . . + a n , n − 1 x n − 1 ( 1 ) ] a n n \large \begin {align} \quad x _ 1 ^ { ( 1 ) } = \frac { b _ 1 - \left [ a _ { 1 2 } x _ 2 ^ { ( 0 ) } + a _ { 1 3 } x _ 3 ^ { ( 0 ) } + a _ { 1 4 } x _ 4 ^ { ( 0 ) } + . . . + a _ { 1 n } x _ n ^ { ( 0 ) } \right ] } { a _ { 1 1 } } \\ x _ 2 ^ { ( 1 ) } = \frac { b _ 2 - \left [ a _ { 2 1 } x _ 1 ^ { ( 1 ) } + a _ { 2 3 } x _ 3 ^ { ( 0 ) } + a _ { 2 4 } x _ 4 ^ { ( 0 ) } + . . . + a _ { 2 n } x _ n ^ { ( 0 ) } \right ] } { a _ { 2 2 } } \\ x _ 3 ^ { ( 1 ) } = \frac { b _ 3 - \left [ a _ { 3 1 } x _ 1 ^ { ( 1 ) } + a _ { 3 2 } x _ 2 ^ { ( 1 ) } + a _ { 3 4 } x _ 4 ^ { ( 0 ) } + . . . + a _ { 3 n } x _ n ^ { ( 0 ) } \right ] } { a _ { 3 3 } } \\ \quad \quad \quad \quad\quad \quad \vdots \quad \quad \quad \quad \quad \quad \\ x _ n ^ { ( 1 ) } = \frac { b _ n - \left [ a _ { n 1 } x _ 1 ^ { ( 1 ) } + a _ { n 2 } x _ 2 ^ { ( 1 ) } + a _ { n 3 } x _ 3 ^ { ( 1 ) } + . . . + a _ { n , n - 1 } x _ { n - 1 } ^ { ( 1 ) } \right ] } { a _ { n n } } \end {align} x 1 ( 1 ) = a 11 b 1 − [ a 12 x 2 ( 0 ) + a 13 x 3 ( 0 ) + a 14 x 4 ( 0 ) + ... + a 1 n x n ( 0 ) ] x 2 ( 1 ) = a 22 b 2 − [ a 21 x 1 ( 1 ) + a 23 x 3 ( 0 ) + a 24 x 4 ( 0 ) + ... + a 2 n x n ( 0 ) ] x 3 ( 1 ) = a 33 b 3 − [ a 31 x 1 ( 1 ) + a 32 x 2 ( 1 ) + a 34 x 4 ( 0 ) + ... + a 3 n x n ( 0 ) ] ⋮ x n ( 1 ) = a nn b n − [ a n 1 x 1 ( 1 ) + a n 2 x 2 ( 1 ) + a n 3 x 3 ( 1 ) + ... + a n , n − 1 x n − 1 ( 1 ) ]
با استفاده از نماد مجموع، برای i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x i ( 1 ) = b i − [ ∑ j = 1 i − 1 a i j x j ( 1 ) + ∑ j = i + 1 n a i j x j ( 0 ) ] a i i \large \begin {align} \quad x _ i ^ { ( 1 ) } = \frac { b _ i - \left [ \sum _ { j = 1 } ^ { i - 1 } a _ { i j } x _ j ^ { (1 ) } + \sum _ { j = i + 1 } ^ { n } a _ { i j } x _ j ^ { ( 0 ) } \right ] } { a _ { i i } } \end {align} x i ( 1 ) = a ii b i − [ ∑ j = 1 i − 1 a ij x j ( 1 ) + ∑ j = i + 1 n a ij x j ( 0 ) ]
به همین ترتیب، برای به دست آوردن تقریب دوم x ( 2 ) x^{(2)} x ( 2 ) x x x
x 1 ( 2 ) = b 1 − [ a 12 x 2 ( 1 ) + a 13 x 3 ( 1 ) + a 14 x 4 ( 1 ) + . . . + a 1 n x n ( 1 ) ] a 11 x 2 ( 2 ) = b 2 − [ a 21 x 1 ( 2 ) + a 23 x 3 ( 1 ) + a 24 x 4 ( 1 ) + . . . + a 2 n x n ( 1 ) ] a 22 x 3 ( 2 ) = b 3 − [ a 31 x 1 ( 2 ) + a 32 x 2 ( 2 ) + a 34 x 4 ( 1 ) + . . . + a 3 n x n ( 1 ) ] a 33 ⋮ x n ( 2 ) = b n − [ a n 1 x 1 ( 2 ) + a n 2 x 2 ( 2 ) + a n 3 x 3 ( 2 ) + . . . + a n , n − 1 x n − 1 ( 2 ) ] a n n \large \begin {align} \quad x _ 1 ^ { ( 2 ) } = \frac { b _ 1 - \left [ a _ { 1 2 } x _ 2 ^ { ( 1 ) } + a _ { 1 3 } x _ 3 ^ { ( 1 ) } + a _ { 1 4 } x _ 4^ { ( 1) } + ... + a _ { 1 n } x _ n ^ { ( 1 ) } \right ] } { a_ { 1 1 } } \\ x _ 2 ^ { ( 2 ) } = \frac { b _ 2 - \left [ a _ { 2 1 } x _ 1 ^ { (2 ) } + a _ { 2 3 } x _ 3 ^ { ( 1 ) } + a _ { 2 4 } x _ 4 ^ { ( 1 ) } + . . . + a _ { 2 n } x _ n ^ { ( 1 ) } \right ] } { a _ { 2 2 } } \\ x _ 3 ^ { ( 2 ) } = \frac { b _ 3 - \left [ a _ { 3 1 } x _ 1 ^ { ( 2 ) } + a _ { 3 2 } x _ 2 ^ { ( 2 ) } + a _ { 3 4 } x _ 4 ^ { ( 1 ) } + ... + a _ { 3 n } x _ n ^ { ( 1 ) } \right ] } { a _ { 3 3 } } \\ \quad \quad \quad \quad\quad \quad \vdots \quad \quad \quad \quad \quad \quad \\ x _ n ^ { ( 2 ) } = \frac { b _ n - \left [ a _ { n 1 } x _ 1 ^ { ( 2 ) } + a _ { n 2 } x _ 2^ { ( 2 ) } + a _ { n 3 } x _ 3 ^ { ( 2 ) } + ... + a _ { n , n - 1 } x _ { n - 1 } ^ { ( 2 ) } \right ] } { a _ { n n } } \end {align} x 1 ( 2 ) = a 11 b 1 − [ a 12 x 2 ( 1 ) + a 13 x 3 ( 1 ) + a 14 x 4 ( 1 ) + ... + a 1 n x n ( 1 ) ] x 2 ( 2 ) = a 22 b 2 − [ a 21 x 1 ( 2 ) + a 23 x 3 ( 1 ) + a 24 x 4 ( 1 ) + ... + a 2 n x n ( 1 ) ] x 3 ( 2 ) = a 33 b 3 − [ a 31 x 1 ( 2 ) + a 32 x 2 ( 2 ) + a 34 x 4 ( 1 ) + ... + a 3 n x n ( 1 ) ] ⋮ x n ( 2 ) = a nn b n − [ a n 1 x 1 ( 2 ) + a n 2 x 2 ( 2 ) + a n 3 x 3 ( 2 ) + ... + a n , n − 1 x n − 1 ( 2 ) ]
با استفاده از نماد مجموع، برای i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x i ( 2 ) = b i − [ ∑ j = 1 i − 1 a i j x j ( 2 ) + ∑ j = i + 1 n a i j x j ( 1 ) ] a i i \large \begin {align} \quad x _ i ^ { ( 2 ) } = \frac { b _ i - \left [ \sum _ { j = 1 } ^ { i - 1 } a _ { i j } x _ j ^ { ( 2 ) } + \sum _ { j = i + 1 } ^ { n } a _ {i j } x _ j ^ { ( 1 ) } \right ] } { a _ { i i } } \end {align} x i ( 2 ) = a ii b i − [ ∑ j = 1 i − 1 a ij x j ( 2 ) + ∑ j = i + 1 n a ij x j ( 1 ) ]
تقریب x x x k ≥ 1 k \ge 1 k ≥ 1 i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n k k k
x 1 ( k ) = b 1 − [ a 12 x 2 ( k − 1 ) + a 13 x 3 ( k − 1 ) + a 14 x 4 ( k − 1 ) + . . . + a 1 n x n ( k − 1 ) ] a 11 x 2 ( k ) = b 2 − [ a 21 x 1 ( k ) + a 23 x 3 ( k − 1 ) + a 24 x 4 ( k − 1 ) + . . . + a 2 n x n ( k − 1 ) ] a 22 x 3 ( k ) = b 3 − [ a 31 x 1 ( k ) + a 32 x 2 ( k ) + a 34 x 4 ( k − 1 ) + . . . + a 3 n x n ( k − 1 ) ] a 33 ⋮ x n ( k ) = b n − [ a n 1 x 1 ( k ) + a n 2 x 2 ( k ) + a n 3 x 3 ( k ) + . . . + a n , n − 1 x n − 1 ( k ) ] a n n \large \begin {align} \quad x _ 1 ^ { ( k ) } = \frac { b _ 1 - \left [ a _ { 1 2 } x _ 2 ^ { ( k -1 ) } + a _ { 1 3 } x _ 3 ^ { ( k - 1 ) } + a _ { 1 4 } x _ 4 ^ { ( k - 1 ) } + . . . + a _ { 1 n } x _ n ^ { ( k - 1 ) } \right ] } { a _ { 1 1 } } \\ x _ 2 ^ { ( k ) } = \frac { b _ 2 - \left [ a _ { 2 1 } x _ 1 ^ { ( k ) } + a _ { 2 3 } x _ 3 ^ { ( k - 1 ) } + a _ { 2 4} x _ 4 ^ { ( k - 1 ) } + . . . + a _ { 2 n } x _ n ^ { ( k - 1 ) } \right ] } { a _ { 2 2 } } \\ x _ 3 ^ { ( k ) } = \frac { b _ 3 - \left [ a _ { 3 1 } x _ 1 ^ { ( k ) } + a _ { 3 2 } x _ 2 ^ { ( k ) } + a _ { 3 4 }x _ 4 ^ { ( k - 1 ) } + . . . + a _ { 3 n } x _ n ^ { ( k - 1 ) } \right ] } { a _ { 3 3 } } \\ \quad \quad \quad \quad\quad \quad \vdots \quad \quad \quad \quad \quad \quad \\ x _ n ^ { ( k ) } = \frac { b _ n - \left [ a _ { n 1 } x _ 1 ^ { ( k ) } + a _ { n 2 } x _ 2 ^ { ( k ) } + a _ { n 3 } x _ 3 ^ { ( k ) } + . . . + a _ { n , n - 1 } x _ { n - 1 } ^ { ( k ) } \right ] } { a _ { n n } } \end {align} x 1 ( k ) = a 11 b 1 − [ a 12 x 2 ( k − 1 ) + a 13 x 3 ( k − 1 ) + a 14 x 4 ( k − 1 ) + ... + a 1 n x n ( k − 1 ) ] x 2 ( k ) = a 22 b 2 − [ a 21 x 1 ( k ) + a 23 x 3 ( k − 1 ) + a 24 x 4 ( k − 1 ) + ... + a 2 n x n ( k − 1 ) ] x 3 ( k ) = a 33 b 3 − [ a 31 x 1 ( k ) + a 32 x 2 ( k ) + a 34 x 4 ( k − 1 ) + ... + a 3 n x n ( k − 1 ) ] ⋮ x n ( k ) = a nn b n − [ a n 1 x 1 ( k ) + a n 2 x 2 ( k ) + a n 3 x 3 ( k ) + ... + a n , n − 1 x n − 1 ( k ) ]
در نهایت، با استفاده از نماد مجموع، برای i = 1 , 2 , . . . , n i = 1, 2, ..., n i = 1 , 2 , ... , n
x i ( k ) = b i − [ ∑ j = 1 i − 1 a i j x j ( k ) + ∑ j = i + 1 n a i j x j ( k − 1 ) ] a i i \large \begin {align} \quad x _ i ^ { ( k ) } = \frac { b _ i - \left [ \sum _ { j = 1 } ^ { i - 1 } a _ { i j } x _ j ^ { ( k ) } + \sum _ { j = i + 1 } ^ { n } a _ { i j } x _ j ^ { ( k -1 ) } \right ] } { a _ { i i } } \end {align} x i ( k ) = a ii b i − [ ∑ j = 1 i − 1 a ij x j ( k ) + ∑ j = i + 1 n a ij x j ( k − 1 ) ]
فرم ماتریسی روش گوس سایدل
در این بخش، فرم ماتریسی روش گوس سایدل را ارائه خواهیم کرد. روش گوس سایدل یک روش تکراری برای حل یک دستگاه مربعی از n n n x \mathbf { x } x
A x = b \large A \mathbf x = \mathbf b A x = b
روش گوس سایدل در حقیقت با تکرار زیر تعریف می‌شود:
L ∗ x ( k + 1 ) = b − U x ( k ) \large L _ * \mathbf { x } ^ { ( k + 1 ) } = \mathbf { b } - U \mathbf { x } ^ { ( k ) } L ∗ x ( k + 1 ) = b − U x ( k )
که در آن، x ( k ) \mathbf{x}^{(k)} x ( k ) k k k x \mathbf {x} x x ( k + 1 ) \mathbf {x} ^ {(k+1)} x ( k + 1 ) k + 1 k + 1 k + 1 x \mathbf {x} x A A A L ∗ L _ * L ∗ U U U A = L ∗ + U A = L _ * + U A = L ∗ + U
برای بررسی جزئیات، A A A x \mathbf {x} x b \mathbf { b } b
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] , x = [ x 1 x 2 ⋮ x n ] , b = [ b 1 b 2 ⋮ b n ] . \large A = \begin {bmatrix} a _ { 1 1 } & a _ { 1 2 } & \cdots & a _ { 1 n } \\ a _ { 2 1 } & a _ { 2 2 } & \cdots & a _ { 2 n } \\ \vdots & \vdots & \ddots & \vdots \\a _ { n 1 } & a _ { n 2 } & \cdots & a _ { n n } \end {bmatrix} , \qquad \mathbf { x } = \begin {bmatrix} x _ { 1 } \\ x _ 2 \\ \vdots \\ x _ n \end {bmatrix} , \qquad \mathbf { b } = \begin {bmatrix} b _ { 1 } \\ b _ 2 \\ \vdots \\ b _ n \end {bmatrix} . A = a 11 a 21 ⋮ a n 1 a 12 a 22 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ a nn , x = x 1 x 2 ⋮ x n , b = b 1 b 2 ⋮ b n .
در ادامه، ماتریس A A A
A = L ∗ + U , L ∗ = [ a 11 0 ⋯ 0 a 21 a 22 ⋯ 0 ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] , U = [ 0 a 12 ⋯ a 1 n 0 0 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 0 ] . \large A = L _ * + U \; , \qquad \text {} \qquad L _ * = \begin {bmatrix} a _ { 1 1 } & 0 & \cdots & 0 \\ a _ { 2 1 } & a _ { 2 2 } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\a _ { n 1 } & a _ { n 2 } & \cdots & a _ { n n } \end {bmatrix} , \quad U = \begin {bmatrix} 0 & a _ { 1 2 } & \cdots & a _ { 1 n } \\ 0 & 0 & \cdots & a _ { 2 n } \\ \vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & 0 \end {bmatrix} . A = L ∗ + U , L ∗ = a 11 a 21 ⋮ a n 1 0 a 22 ⋮ a n 2 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ a nn , U = 0 0 ⋮ 0 a 12 0 ⋮ 0 ⋯ ⋯ ⋱ ⋯ a 1 n a 2 n ⋮ 0 .
دستگاه معادلات خطی را می‌توان به صورت زیر بازنویسی کرد:
L ∗ x = b − U x \large L _ * \mathbf { x } = \mathbf { b } - U \mathbf { x } L ∗ x = b − U x
در اینجا، با استفاده از روش گوس سایدل، x \mathbf { x } x x \mathbf{x} x
x ( k + 1 ) = L ∗ − 1 ( b − U x ( k ) ) . \large \mathbf { x } ^ { ( k + 1) } = L _ * ^ { - 1 } ( \mathbf { b } - U \mathbf { x } ^ { ( k ) } ) . x ( k + 1 ) = L ∗ − 1 ( b − U x ( k ) ) .
اما با بهره‌گیری از فرم مثلثی L ∗ L _ * L ∗ x ( k + 1 ) \mathbf { x } ^ {(k+1)} x ( k + 1 )
x i ( k + 1 ) = 1 a i i ( b i − ∑ j = 1 i − 1 a i j x j ( k + 1 ) − ∑ j = i + 1 n a i j x j ( k ) ) , i = 1 , 2 , … , n . \large x ^ { ( k + 1 ) } _ i = \frac { 1 } { a _ { i i } } \left ( b _ i - \sum _ { j = 1} ^ { i - 1 } a _ { i j } x ^ { ( k + 1 ) } _ j - \sum _ { j = i + 1 } ^ { n } a _ { i j } x ^ { ( k ) }_ j \right ) , \quad i = 1 , 2 , \dots , n . x i ( k + 1 ) = a ii 1 b i − j = 1 ∑ i − 1 a ij x j ( k + 1 ) − j = i + 1 ∑ n a ij x j ( k ) , i = 1 , 2 , … , n .
این روند تا جایی ادامه پیدا می‌کند که تغییرات حاصل از تکرار به مقداری کمتر از یک مقدار مشخص برسد. می‌بینیم که فرمول روش گوس سایدل بسیار شبیه به روش ژاکوبی است.
در محاسبه x ( k + 1 ) { \mathbf{x}} ^ { ( k + 1 )} x ( k + 1 ) x ( k + 1 ) \mathbf {x } ^ { ( k + 1 )} x ( k + 1 ) x ( k ) \mathbf { x } ^ { (k)} x ( k ) k + 1 k +1 k + 1
البته، برخلاف روش ژاکوبی، محاسبات مربوط به هر مؤلفه را نمی‌توان به صورت موازی انجام داد. علاوه بر این، مقادیر هر تکرار به مرتبه معادلات اصلی بستگی دارند.
همگرایی روش گوس سایدل
ویژگی‌های همگرایی روش گوس سایدل به ماتریس A A A
حتی اگر شرایط مذکور بالا برقرار نباشند، گاهی روش گوس سایدل همگرا می‌شود.
مثال‌های روش گوس سایدل
در این بخش، چند مثال را از روش گوس سایدل بررسی می‌کنیم.
مثال ۱
دستگاه خطی A x = b A\mathbf { x } = \mathbf { b } A x = b
A = [ 16 3 7 − 11 ] , b = [ 11 13 ] . \large A = \begin {bmatrix} 16 & 3 \\ 7 & - 1 1 \\ \end {bmatrix} \; , \; \; \; \; b = \begin {bmatrix} 1 1 \\ 1 3 \end {bmatrix} . A = [ 16 7 3 − 11 ] , b = [ 11 13 ] .
می‌خواهیم از معادله x ( k + 1 ) = L ∗ − 1 ( b − U x ( k ) ) \mathbf { x } ^ { ( k + 1 ) } = L _ * ^ { - 1 } ( \mathbf { b } - U \mathbf { x } ^ { ( k ) } ) x ( k + 1 ) = L ∗ − 1 ( b − U x ( k ) )
x ( k + 1 ) = T x ( k ) + C \large \mathbf { x } ^ { ( k + 1 ) } = T \mathbf { x } ^ { ( k ) } + C x ( k + 1 ) = T x ( k ) + C
که در آن، T = − L ∗ − 1 U T = - L _ * ^ { - 1} U T = − L ∗ − 1 U C = L ∗ − 1 b C = L _ * ^ { - 1 } \mathbf { b } C = L ∗ − 1 b
باید ماتریس A A A L ∗ L _ * L ∗ U U U
L ∗ = [ 16 0 7 − 11 ] , U = [ 0 3 0 0 ] . \large L _ * = \begin {bmatrix} 1 6 & 0 \\ 7 & - 1 1 \\ \end {bmatrix} \;\; , \; \; \; \; U = \begin {bmatrix} 0 & 3 \\ 0 & 0 \end {bmatrix} . L ∗ = [ 16 7 0 − 11 ] , U = [ 0 0 3 0 ] .
معکوس ماتریس L ∗ L _ * L ∗
L ∗ − 1 = [ 16 0 7 − 11 ] − 1 = [ 0.0625 0.0000 0.0398 − 0.0909 ] \large L _ * ^ { - 1 } = \begin {bmatrix} 1 6 & 0 \\ 7 & - 1 1 \end {bmatrix} ^ { - 1 } = \begin {bmatrix} 0 . 0 6 2 5 & 0 . 0 0 0 0 \\ 0 . 0 3 9 8 & - 0 . 0 9 0 9 \\ \end {bmatrix} L ∗ − 1 = [ 16 7 0 − 11 ] − 1 = [ 0.0625 0.0398 0.0000 − 0.0909 ]
بنابراین، خواهیم داشت:
T = − [ 0.0625 0.0000 0.0398 − 0.0909 ] × [ 0 3 0 0 ] = [ 0.000 − 0.1875 0.000 − 0.1194 ] , \large T = - \begin {bmatrix} 0 . 0 6 2 5 & 0 . 0 0 0 0 \\ 0.0398 & -0.0909 \end {bmatrix} \times \begin {bmatrix} 0 & 3 \\ 0 & 0 \end {bmatrix} = \begin {bmatrix} 0 . 0 0 0 & - 0 .1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 4 \end {bmatrix} , T = − [ 0.0625 0.0398 0.0000 − 0.0909 ] × [ 0 0 3 0 ] = [ 0.000 0.000 − 0.1875 − 0.1194 ] ,
C = [ 0.0625 0.0000 0.0398 − 0.0909 ] × [ 11 13 ] = [ 0.6875 − 0.7439 ] . \large C = \begin {bmatrix} 0 . 0 6 2 5 & 0 . 0 0 0 0 \\ 0 . 0 3 9 8 & - 0 . 0 9 0 9 \end {bmatrix} \times \begin {bmatrix} 1 1 \\ 1 3 \end {bmatrix} = \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 3 9 \end {bmatrix} . C = [ 0.0625 0.0398 0.0000 − 0.0909 ] × [ 11 13 ] = [ 0.6875 − 0.7439 ] .
اکنون T T T C C C x \mathbf { x } x x ( 0 ) \mathbf{x}^{(0)} x ( 0 )
بنابراین، حدس اولیه را به صورت زیر انتخاب می‌کنیم:
x ( 0 ) = [ 1.0 1.0 ] . \large x ^ { ( 0 ) } = \begin {bmatrix} 1 . 0 \\ 1 . 0 \end {bmatrix} . x ( 0 ) = [ 1.0 1.0 ] .
در نتیجه، خواهیم داشت:
x ( 1 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 1.0 1.0 ] + [ 0.6875 − 0.7443 ] = [ 0.5000 − 0.8636 ] . x ( 2 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 0.5000 − 0.8636 ] + [ 0.6875 − 0.7443 ] = [ 0.8494 − 0.6413 ] . x ( 3 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 0.8494 − 0.6413 ] + [ 0.6875 − 0.7443 ] = [ 0.8077 − 0.6678 ] . x ( 4 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 0.8077 − 0.6678 ] + [ 0.6875 − 0.7443 ] = [ 0.8127 − 0.6646 ] . x ( 5 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 0.8127 − 0.6646 ] + [ 0.6875 − 0.7443 ] = [ 0.8121 − 0.6650 ] . x ( 6 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 0.8121 − 0.6650 ] + [ 0.6875 − 0.7443 ] = [ 0.8122 − 0.6650 ] . x ( 7 ) = [ 0.000 − 0.1875 0.000 − 0.1193 ] × [ 0.8122 − 0.6650 ] + [ 0.6875 − 0.7443 ] = [ 0.8122 − 0.6650 ] . \large \begin {align*} x ^ { ( 1 ) } & = \begin {bmatrix} 0 . 0 0 0 & - 0 . 1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 1 . 0 \\ 1 . 0 \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 5 0 0 0 \\ - 0 . 8 6 3 6 \end {bmatrix} . \\ x ^ { ( 2 ) } & = \begin {bmatrix} 0 . 0 0 0 & - 0 . 1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 0 . 5 0 0 0 \\ - 0 . 8 6 3 6 \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 8 4 9 4 \\ - 0 . 6 4 1 3 \end {bmatrix} . \\ x ^ { ( 3 ) } & = \begin {bmatrix} 0 . 0 0 0 & - 0 . 1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 0 . 8 4 9 4 \\ - 0 . 6 4 1 3 \\ \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 8 0 7 7 \\ - 0 . 6 6 7 8 \end {bmatrix} . \\ x ^ { ( 4 ) } & = \begin {bmatrix} 0 . 0 0 0 & - 0 . 1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 0 . 8 0 7 7 \\ - 0 . 6 6 7 8 \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 8 1 2 7 \\ - 0 . 6 6 4 6 \end {bmatrix} . \\ x ^ { ( 5 ) } & = \begin {bmatrix} 0 . 0 0 0 & - 0 . 1 87 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 0 . 8 1 2 7 \\ - 0 . 6 6 4 6 \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 8 1 2 1 \\ - 0 . 6 6 5 0 \end {bmatrix} . \\ x ^ { ( 6 ) } & = \begin {bmatrix} 0 .0 0 0 & - 0 . 1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 0 . 8 1 2 1 \\ - 0 .6 6 5 0 \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 8 1 2 2 \\ - 0 . 6 6 5 0 \end {bmatrix} . \\ x ^ { ( 7 ) } & = \begin {bmatrix} 0 . 0 0 0 & - 0 . 1 8 7 5 \\ 0 . 0 0 0 & - 0 . 1 1 9 3 \end {bmatrix} \times \begin {bmatrix} 0 . 8 1 2 2 \\ - 0 . 6 6 5 0 \end {bmatrix} + \begin {bmatrix} 0 . 6 8 7 5 \\ - 0 . 7 4 4 3 \end {bmatrix} = \begin {bmatrix} 0 . 8 1 2 2 \\ - 0 . 6 6 5 0 \end {bmatrix} . \end {align*} x ( 1 ) x ( 2 ) x ( 3 ) x ( 4 ) x ( 5 ) x ( 6 ) x ( 7 ) = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 1.0 1.0 ] + [ 0.6875 − 0.7443 ] = [ 0.5000 − 0.8636 ] . = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 0.5000 − 0.8636 ] + [ 0.6875 − 0.7443 ] = [ 0.8494 − 0.6413 ] . = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 0.8494 − 0.6413 ] + [ 0.6875 − 0.7443 ] = [ 0.8077 − 0.6678 ] . = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 0.8077 − 0.6678 ] + [ 0.6875 − 0.7443 ] = [ 0.8127 − 0.6646 ] . = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 0.8127 − 0.6646 ] + [ 0.6875 − 0.7443 ] = [ 0.8121 − 0.6650 ] . = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 0.8121 − 0.6650 ] + [ 0.6875 − 0.7443 ] = [ 0.8122 − 0.6650 ] . = [ 0.000 0.000 − 0.1875 − 0.1193 ] × [ 0.8122 − 0.6650 ] + [ 0.6875 − 0.7443 ] = [ 0.8122 − 0.6650 ] .
همان‌طور که انتظار می‌رود، الگوریتم به جواب دقیق همگرا می‌شود:
x = A − 1 b ≈ [ 0.8122 − 0.6650 ] . \large \mathbf { x } = A ^ { - 1 } \mathbf { b } \approx \begin {bmatrix} 0 . 8 1 2 2 \\ - 0 . 6 6 5 0 \end {bmatrix} . x = A − 1 b ≈ [ 0.8122 − 0.6650 ] .
در حقیقت، ماتریس A A A
مثال ۲
دستگاه خطی A x = b A \mathbf { x } = \mathbf { b } A x = b
A = [ 2 3 5 7 ] , b = [ 11 13 ] . \large A = \begin {bmatrix} 2 & 3 \\ 5 & 7 \\ \end {bmatrix} \; , \; \; \; b = \begin {bmatrix} 1 1 \\ 1 3 \\ \end {bmatrix} . A = [ 2 5 3 7 ] , b = [ 11 13 ] .
می‌خواهیم از معادله x ( k + 1 ) = L ∗ − 1 ( b − U x ( k ) ) \mathbf { x } ^ { ( k + 1 ) } = L _ * ^ { - 1 } ( \mathbf { b } - U \mathbf { x } ^ { ( k ) } ) x ( k + 1 ) = L ∗ − 1 ( b − U x ( k ) )
x ( k + 1 ) = T x ( k ) + C \large \mathbf { x } ^ { ( k + 1 ) } = T \mathbf { x } ^ { ( k ) } + C x ( k + 1 ) = T x ( k ) + C
که در آن، T = − L ∗ − 1 U T = - L _ * ^ { - 1} U T = − L ∗ − 1 U C = L ∗ − 1 b C = L _ * ^ { - 1 } \mathbf { b } C = L ∗ − 1 b
باید ماتریس A A A L ∗ L _ * L ∗ U U U
L ∗ = [ 2 0 5 7 ] , U = [ 0 3 0 0 ] . \large L _ * = \begin {bmatrix} 2 & 0 \\ 5 & 7 \\ \end {bmatrix} \; , \; \; \;\; U = \begin {bmatrix} 0 & 3 \\ 0 & 0 \\ \end {bmatrix} . L ∗ = [ 2 5 0 7 ] , U = [ 0 0 3 0 ] .
معکوس ماتریس L ∗ L _ * L ∗
L ∗ − 1 = [ 2 0 5 7 ] − 1 = [ 0.500 0.000 − 0.357 0.143 ] . \large L _ * ^ { - 1 } = \begin {bmatrix} 2 & 0 \\ 5 & 7 \\ \end {bmatrix} ^ { - 1 } = \begin {bmatrix} 0 . 5 0 0 & 0 . 0 0 0 \\ - 0 . 3 5 7 & 0 . 1 4 3 \\ \end {bmatrix} . L ∗ − 1 = [ 2 5 0 7 ] − 1 = [ 0.500 − 0.357 0.000 0.143 ] .
بنابراین، خواهیم داشت:
T = − [ 0.500 0.000 − 0.357 0.143 ] × [ 0 3 0 0 ] = [ 0.000 − 1.500 0.000 1.071 ] , C = [ 0.500 0.000 − 0.357 0.143 ] × [ 11 13 ] = [ 5.500 − 2.071 ] . \large \begin {align*} T & = - \begin {bmatrix} 0 . 5 0 0 & 0 . 0 0 0 \\ - 0 . 3 5 7 & 0 . 1 4 3 \\ \end {bmatrix} \times \begin {bmatrix} 0 & 3 \\ 0 & 0 \\ \end {bmatrix} = \begin {bmatrix} 0 . 0 0 0 & - 1 . 5 0 0 \\ 0 . 0 0 0 & 1 . 0 7 1 \\ \end {bmatrix} , \\ C & = \begin {bmatrix} 0 . 5 0 0 & 0 . 0 0 0 \\ - 0 . 3 5 7 & 0 . 1 4 3 \\ \end {bmatrix} \times \begin {bmatrix} 1 1 \\ 1 3 \\ \end {bmatrix} = \begin {bmatrix} 5 . 5 0 0 \\ - 2 . 0 7 1 \\ \end {bmatrix} . \end {align*} T C = − [ 0.500 − 0.357 0.000 0.143 ] × [ 0 0 3 0 ] = [ 0.000 0.000 − 1.500 1.071 ] , = [ 0.500 − 0.357 0.000 0.143 ] × [ 11 13 ] = [ 5.500 − 2.071 ] .
اکنون T T T C C C x \mathbf { x } x x ( 0 ) \mathbf{x}^{(0)} x ( 0 )
بنابراین، حدس اولیه را به صورت زیر انتخاب می‌کنیم:
x ( 0 ) = [ 1.1 2.3 ] . \large x ^ { ( 0 ) } = \begin {bmatrix} 1 . 1 \\ 2 . 3 \\ \end {bmatrix} . x ( 0 ) = [ 1.1 2.3 ] .
در نتیجه، خواهیم داشت:
x ( 1 ) = [ 0 − 1.500 0 1.071 ] × [ 1.1 2.3 ] + [ 5.500 − 2.071 ] = [ 2.050 0.393 ] . x ( 2 ) = [ 0 − 1.500 0 1.071 ] × [ 2.050 0.393 ] + [ 5.500 − 2.071 ] = [ 4.911 − 1.651 ] . x ( 3 ) = ⋯ . \large \begin {align*} x ^ { ( 1 ) } & = \begin{bmatrix} 0 & - 1 . 5 0 0 \\ 0 & 1 . 0 7 1 \\ \end {bmatrix} \times \begin {bmatrix} 1 . 1 \\ 2 . 3 \\ \end {bmatrix} + \begin {bmatrix} 5 .5 0 0 \\ - 2 . 0 7 1 \\ \end {bmatrix} = \begin {bmatrix} 2 . 0 5 0 \\ 0 . 3 9 3 \\ \end {bmatrix} . \\ x ^ { ( 2 ) } & = \begin {bmatrix} 0 & - 1 . 5 0 0 \\ 0 & 1 . 0 7 1 \\ \end {bmatrix} \times \begin {bmatrix} 2 . 0 5 0 \\ 0 . 3 9 3 \\ \end {bmatrix} + \begin {bmatrix} 5 .5 0 0 \\ - 2 . 0 7 1 \\ \end {bmatrix} = \begin {bmatrix} 4 . 9 1 1 \\ - 1 . 6 5 1 \\ \end {bmatrix} . \\ x ^ { ( 3 ) } & = \cdots . \, \end {align*} x ( 1 ) x ( 2 ) x ( 3 ) = [ 0 0 − 1.500 1.071 ] × [ 1.1 2.3 ] + [ 5.500 − 2.071 ] = [ 2.050 0.393 ] . = [ 0 0 − 1.500 1.071 ] × [ 2.050 0.393 ] + [ 5.500 − 2.071 ] = [ 4.911 − 1.651 ] . = ⋯ .
اگر همگرایی را آزمایش کنیم، خواهیم دید که الگوریتم واگرا می‌شود. در واقع، ماتریس A A A
x = A − 1 b = [ − 38 29 ] \large \mathbf { x } = A ^ { - 1 } \mathbf { b } = \begin {bmatrix} - 3 8 \\ 2 9 \end {bmatrix} x = A − 1 b = [ − 38 29 ]
مثال ۳
فرض کنید k k k x n \mathbf {x} _ n x n x 0 \mathbf { x } _ 0 x 0 x 1 \mathbf { x } _ 1 x 1 c n + 1 c _ { n + 1 } c n + 1 c n + 2 c _{n + 2 } c n + 2 x n x _ n x n x \mathbf { x } x
برای روشن شدن موضوع، مثال زیر را در نظر بگیرید.
10 x 1 − x 2 + 2 x 3 = 6 , − x 1 + 11 x 2 − x 3 + 3 x 4 = 25 , 2 x 1 − x 2 + 10 x 3 − x 4 = − 11 , 3 x 2 − x 3 + 8 x 4 = 15. \begin {array} {rrrrl} 1 0 x _ 1 & - x _ 2 & + 2 x _ 3 & & = 6 , \\ - x _ 1 & + 1 1 x _ 2 & - x _ 3 & + 3 x _ 4 & = 2 5 , \\ 2 x _ 1 & - x _ 2 & + 1 0 x _ 3 & - x _ 4 & = - 1 1 , \\ & 3 x _ 2 & - x _ 3 & + 8 x _ 4 & = 1 5 . \end {array} 10 x 1 − x 1 2 x 1 − x 2 + 11 x 2 − x 2 3 x 2 + 2 x 3 − x 3 + 10 x 3 − x 3 + 3 x 4 − x 4 + 8 x 4 = 6 , = 25 , = − 11 , = 15.
مجهولات x 1 x _ 1 x 1 x 2 x _ 2 x 2 x 3 x _ 3 x 3 x 4 x _ 4 x 4
x 1 = x 2 / 10 − x 3 / 5 + 3 / 5 , x 2 = x 1 / 11 + x 3 / 11 − 3 x 4 / 11 + 25 / 11 , x 3 = − x 1 / 5 + x 2 / 10 + x 4 / 10 − 11 / 10 , x 4 = − 3 x 2 / 8 + x 3 / 8 + 15 / 8. \large \begin {align} x _ 1 & = x _ 2 / 1 0 - x _ 3 / 5 + 3 / 5 , \\ x _ 2 & = x _ 1 / 1 1 + x _ 3 / 11 - 3 x _ 4 / 11 + 25 / 11 , \\ x _ 3 & = - x _ 1 / 5 + x _ 2 / 10 + x _ 4 /10 - 11 / 10 , \\ x _ 4 & = - 3 x _ 2 /8 + x _ 3 / 8 + 1 5 / 8 . \end {align} x 1 x 2 x 3 x 4 = x 2 /10 − x 3 /5 + 3/5 , = x 1 /11 + x 3 /11 − 3 x 4 /11 + 25/11 , = − x 1 /5 + x 2 /10 + x 4 /10 − 11/10 , = − 3 x 2 /8 + x 3 /8 + 15/8.
تقریب اولیه را ( 0 , 0 , 0 , 0 ) ( 0, 0 , 0 , 0 ) ( 0 , 0 , 0 , 0 )
x 1 = 3 / 5 = 0.6 , x 2 = ( 3 / 5 ) / 11 + 25 / 11 = 3 / 55 + 25 / 11 = 2.3272 , x 3 = − ( 3 / 5 ) / 5 + ( 2.3272 ) / 10 − 11 / 10 = − 3 / 25 + 0.23272 − 1.1 = − 0.9873 , x 4 = − 3 ( 2.3272 ) / 8 + ( − 0.9873 ) / 8 + 15 / 8 = 0.8789. \large \begin {align} x _ 1 & = 3 / 5 = 0 . 6 , \\ x _ 2 & = ( 3 / 5 ) / 1 1 + 2 5 / 1 1 = 3 / 55 + 25 / 11 = 2.3272, \\ x _ 3 & = - ( 3 / 5 ) / 5 + ( 2 . 3 2 7 2 ) / 10 - 11/ 10 = - 3 / 25 + 0 . 2 3272 - 1.1 = - 0. 9 8 7 3 , \\ x _ 4 & = - 3 ( 2.3272 ) / 8 + ( - 0.9873 ) / 8 + 1 5 / 8 = 0.8789 . \end {align} x 1 x 2 x 3 x 4 = 3/5 = 0.6 , = ( 3/5 ) /11 + 25/11 = 3/55 + 25/11 = 2.3272 , = − ( 3/5 ) /5 + ( 2.3272 ) /10 − 11/10 = − 3/25 + 0.23272 − 1.1 = − 0.9873 , = − 3 ( 2.3272 ) /8 + ( − 0.9873 ) /8 + 15/8 = 0.8789.
با استفاده از تقریب‌های به دست آمده، روند تکراری تا زمانی ادامه پیدا می‌کند که دقت مطلوب حاصل شود. جواب‌های تقریبی زیر بعد از چهار تکرار به دست آمده‌اند.
x 1 x 2 x 3 x 4 0.6 2.32727 − 0.987273 0.878864 1.03018 2.03694 − 1.01446 0.984341 1.00659 2.00356 − 1.00253 0.998351 1.00086 2.0003 − 1.00031 0.99985 \large \begin {array} {llll} x _ 1 & x _ 2 & x _ 3 & x _ 4 \\ \hline 0 . 6 & 2 . 3 2 7 2 7 & - 0 . 9 8 7 2 7 3 & 0 . 8 7 8 8 6 4 \\ 1 . 0 3 0 1 8 & 2 . 0 36 9 4 & - 1 . 0 1 4 4 6 & 0 .9 8 43 4 1 \\ 1. 0 06 5 9 & 2 . 0 03 5 6 & - 1 . 0 0 2 5 3 & 0 . 9 9 8 3 5 1 \\ 1 . 0 0 0 8 6 & 2 . 0 0 0 3 & - 1 . 0 0 0 3 1 & 0 . 9 9 9 8 5 \end {array} x 1 0.6 1.03018 1.00659 1.00086 x 2 2.32727 2.03694 2.00356 2.0003 x 3 − 0.987273 − 1.01446 − 1.00253 − 1.00031 x 4 0.878864 0.984341 0.998351 0.99985
جواب دقیق دستگاه ( 1 , 2 , − 1 , 1 ) ( 1 , 2 , - 1 , 1 ) ( 1 , 2 , − 1 , 1 )
الگوریتم پیاده‌سازی روش گوس سایدل
از آنجایی که عناصری را که قبلاً محاسبه شده‌اند می‌توان بازنویسی و جایگزین کرد، فقط به یک بردار ذخیره‌سازی نیاز است و نمایه‌سازی بردار حذف می‌شود. الگوریتم روش گوس سایدل به شرح زیر است:
پیاده‌سازی روش گوس سایدل در پایتون
برنامه زیر، کد پایتون روش گوس سایدل را نشان می‌دهد.
خروجی حاصل از اجرای این برنامه به صورت زیر است:
System of equations :
[ 10 * x1 + - 1 * x2 + 2 * x3 + 0 * x4 ] = [ 6 ]
[ - 1 * x1 + 11 * x2 + - 1 * x3 + 3 * x4 ] = [ 25 ]
[ 2 * x1 + - 1 * x2 + 10 * x3 + - 1 * x4 ] = [ - 11 ]
[ 0 * x1 + 3 * x2 + - 1 * x3 + 8 * x4 ] = [ 15 ]
Iteration 1 : [ 0. 0. 0. 0. ]
Iteration 2 : [ 0.6 2.32727273 - 0.98727273 0.87886364 ]
Iteration 3 : [ 1.03018182 2.03693802 - 1.0144562 0.98434122 ]
Iteration 4 : [ 1.00658504 2.00355502 - 1.00252738 0.99835095 ]
Iteration 5 : [ 1.00086098 2.00029825 - 1.00030728 0.99984975 ]
Iteration 6 : [ 1.00009128 2.00002134 - 1.00003115 0.9999881 ]
Iteration 7 : [ 1.00000836 2.00000117 - 1.00000275 0.99999922 ]
Iteration 8 : [ 1.00000067 2.00000002 - 1.00000021 0.99999996 ]
Iteration 9 : [ 1.00000004 1.99999999 - 1.00000001 1. ]
Iteration 10 : [ 1. 2. - 1. 1. ]
Solution : [ 1. 2. - 1. 1. ]
Error : [ 2.06480930e-08 - 1.25551054e-08 3.61417563e-11 0.00000000e+00 ]
پیاده‌سازی روش گوس سایدل در متلب
کد کوتاه زیر، برنامه حل دستگاه با تعداد معادلات دلخواه و با استفاده از روش گوس سایدل در متلب است که در آن، از فرمول زیر استفاده شده است:
x i ( k + 1 ) = 1 a i i ( b i − ∑ j < i a i j x j ( k + 1 ) − ∑ j > i a i j x j ( k ) ) , i , j = 1 , 2 , … , n \large x ^ { ( k + 1 ) } _ i = \frac { 1 } { a _ { i i } } \left ( b _ i - \sum _ { j < i } a _ { i j } x ^ { ( k + 1 ) } _ j - \sum _ { j > i } a _ { i j } x ^ { ( k) } _ j \right ) , \quad i, j = 1 , 2 , \ldots , n x i ( k + 1 ) = a ii 1 b i − j < i ∑ a ij x j ( k + 1 ) − j > i ∑ a ij x j ( k ) , i , j = 1 , 2 , … , n
برنامه مربوط به فرمول بالا در متلب، به سادگی به صورت زیر نوشته می‌شود:
برنامه متلب زیر نیز یک نسخه دیگر از روش گوس سایدل است که در آن، از فرم ماتریسی استفاده شده است:
پیاده‌سازی روش گوس سایدل در C
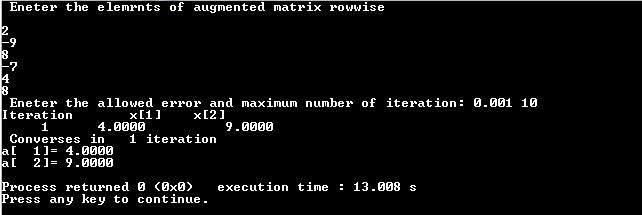
کد زیر، پیاده‌سازی روش گوس سایدل در زبان برنامه‌نویسی C را نشان می‌دهد.
خروجی حاصل از اجرای این برنامه به صورت زیر خواهد بود:
اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
^^
فرادرس
سلام آقای حمیدی وقتتون بخیر امیدوارم حالتون خوب باشه و خدا قوت برای تلاشتون
یک سوال این وسط پیش میاد اگر ما یک ماتریس n×n قطری غالب و مثبت معین داشته باشیم برای n بالای 2000 برای همگرا شدن به جواب ممکنه چند تکرار صورت بگیره
میدونم بستگی به ارور مشخص شده داره ولی ممکنه این تو متلب چقدر طول بکشه ؟
بازم ممنون
به اون آقایی که واسه ژاکوبی تو متلب با مثال رو‌فیلم توضیح میداد بگین واسه گوس سایدل تو متلب هم همینطوری توضیح بدن ممنون☹️?
خیلی عالی و مفید. خسته نباشید.