جستجوی دودویی – به زبان ساده

در این مطلب، الگوریتم جستجوی دودویی (Binary Search) مورد بررسی قرار گرفته و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون انجام شده است.

جستجوی دودویی

در جستجوی دودویی (Binary Search)‌، جستجو در یک آرایه مرتب شده، با تقسیم تکرار شونده بازه جستجو به نصف، انجام می‌شود. کار با بازه‌ای که کل آرایه را پوشش می‌دهد، آغاز می‌شود. اگر مقدار کلید جستجو برابر با عنصر میانی باشد، اندیس آن بازگردانده می‌شود.

فیلم آموزش درخت جستجوی دودویی (AVL) در ساختمان داده ها (رایگان) در فرادرس

کلیک کنید

در غیر این صورت، اگر مقدار کلید جستجو کمتر از عنصری باشد که در میانه بازه قرار دارد، بازه شکسته شده و جستجو در نیمه کمتر ادامه پیدا می‌کند. در صورتی که مقدار کلید جستجو بزرگ‌تر از اندیس میانی آرایه باشد، جستجو در نیمه بیشتر (حاوی مقادیر بزرگ‌تر) آرایه ادامه پیدا می‌کند. کار شکستن آرایه به دو نیم و انتخاب نیمه‌ای که جستجو باید در آن انجام شود، مکررا و تا هنگامی که عنصر مورد نظر در آرایه یافته شود و یا مشخص شود که عنصر مورد نظر در آرایه وجود ندارد، ادامه خواهد داشت.

مثالی از جستجوی دودویی

آرایه مرتب شده []arr شامل n عنصر موجود است. هدف، نوشتن تابعی است که یک عنصر داده شده x را در آرایه مذکور ([]arr) جستجو کند. یک رویکرد ساده برای انجام این کار، استفاده از «جستجوی خطی» (Linear Search) است. پیچیدگی زمانی الگوریتم جستجوی خطی، (O(n است.

رویکرد دیگر، انجام کار مشابهی با استفاده از «جستجوی دودویی» (Binary Search) است. ایده اصلی نهفته در پس جستجوی دودویی، استفاده از اطلاعات موجود در آرایه مرتب شده و کاهش پیچیدگی زمانی به (O(Log n است. در جستجوی دودویی اساسا نیمی از عناصر تنها پس از یک مقایسه حذف می‌شوند. برای انجام جستجو، از الگوریتم زیر استفاده می‌شود.

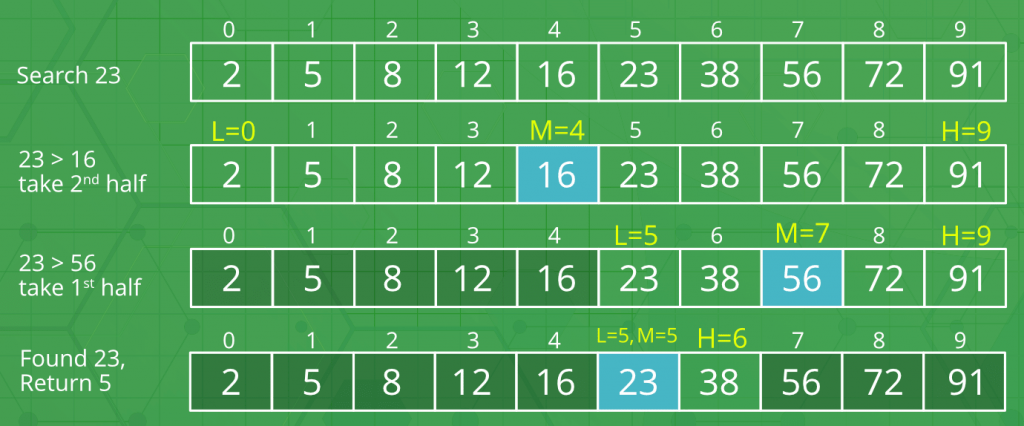
1. x با عنصر میانی آرایه مقایسه می‌شود.
2. اگر x با عنصر میانی آرایه یکی بود، اندیس عنصر میانی را بازگردان.
3. در غیر این صورت، اگر x بزرگ‌تر از عنصر میانی بود، امکان دارد x در نیمه سمت راست آرایه، پس از عنصر میانی، قرار داشته باشد (شایان توجه است که همانطور که پیش‌تر اشاره شد، آرایه مرتب شده است. پس در این حالت، نیمه‌ای با مقادیر بزرگ‌تر برای ادامه جستجو گزینش می‌شود).
4. در غیر این صورت، اگر x از عنصر میانی آرایه کوچک‌تر باشد، آرایه به دو نیمه شکسته شده و جستجو در نیمه سمت چپ (با مقادیر کوچک‌تر از میانه)، ادامه پیدا می‌کند.

در ادامه، پیاده‌سازی الگوریتم جستجوی دودویی به صورت بازگشتی، در زبان‌های برنامه‌نویسی C++ ،C، «جاوا» (Java)، «پایتون» (Python)، «سی‌شارپ» (#C) و PHP ارائه شده است.

کد بازگشتی الگوریتم جستجوی دودویی در C

کد بازگشتی الگوریتم جستجوی دودویی در ++C

کد بازگشتی الگوریتم جستجوی دودویی در جاوا

کد بازگشتی الگوریتم جستجوی دودویی در پایتون

کد بازگشتی الگوریتم جستجوی دودویی در #C

کد بازگشتی الگوریتم جستجوی دودویی در PHP

خروجی

Element is present at index 3

در ادامه، کد مربوط به پیاده‌سازی الگوریتم جستجوی دودویی به صورت «تکرار شونده» (Iterative) ارائه شده است.

فیلم آموزش ساختمان داده ها – مرور و تست کنکور ارشد در فرادرس

کلیک کنید

کد تکرار شونده الگوریتم جستجوی دودویی در C

کد تکرار شونده الگوریتم جستجوی دودویی در ++C

کد تکرار شونده الگوریتم جستجوی دودویی در جاوا

کد تکرار شونده الگوریتم جستجوی دودویی در پایتون

کد تکرار شونده الگوریتم جستجوی دودویی در #C

کد تکرار شونده الگوریتم جستجوی دودویی در PHP

خروجی

Element is present at index 3

پیچیدگی زمانی

پیچیدگی زمانی جستجوی دودویی را می‌توان به صورت زیر نوشت:

T(n) = T(n/2) + c

رابطه بازگشتی بالا را می‌توان با استفاده از روش «درخت بازگشتی» (Recursive tree) یا «قضیه اصلی واکاوی (تحلیل) الگوریتم‌ها» (Master method) حل کرد. این رابطه، در حالت دوم قضیه اصلی تحلیل الگوریتم‌ها صدق می‌کند و راهکار بازگشتی به صورت (Theta(Logn است.

«فضای کمکی» (Auxiliary Space)، اگر پیاده‌سازی به صورت تکرار شونده باشد برابر با  (O(1 و در صورتی که بازگشتی باشد، از مرتبه (O(Logn فضای پشته فراخوانی بازگشتی است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده
• الگوریتم جست و جوی دودویی در جاوا اسکریپت — به زبان ساده

^^