الگوریتم های مهم پایتون که باید آنها را بدانید — راهنمای کاربردی

برخی الگوریتم‌های خاص هستند که استفاده زیادی در زمان برنامه‌نویسی دارند. در این راهنما به بررسی چند الگوریتم مهم پایتون که جزء رایج‌ترین انواع این الگوریتم‌ها هستند به همراه مثال می‌پردازیم. این الگوریتم‌ها شامل جستجو، مرتب‌سازی و افزودن/حذف کردن آیتم به لیست پیوندی هستند. ایده‌های پیرامون این مثال‌ها در مورد الگوریتم‌های زیاد دیگری نیز صدق می‌کند. درک این سه مثال و الگوریتم به شما کمک می‌کنند تا اطلاعات خوبی در مورد روش برخورد با مسائل مرتبط با الگوریتم‌های دیگر نیز کسب کنید و در این زمینه اعتماد به نفس داشته باشید.

جستجوی دودویی

«جستجوی دودویی» (Binary Search) یک الگوریتم ضروری جستجو است که روی آرایه‌های مرتب اجرا می‌شود و اندیس یک مقدار را که به دنبالش هستیم بازگشت می‌دهد. این کار به صورت زیر اجرا می‌شود:

1. نقطه میانی آرایه مرتب را پیدا کنید.
2. نقطه میانی را با مقدار مورد نظر مقایسه کنید.
3. اگر نقطه میانی بزرگ‌تر از مقدار مورد نظر باشد، جستجوی باینری در نیمه راست آرایه تکرار می‌شود.
4. اگر نقطه میانی کوچک‌تر از مقدار مورد جستجو باشد، جستجوی باینری روی نیمه چپ آرایه تکرار می‌شود.
5. این مراحل را تا زمانی که نقطه میانی برابر با مقدار مورد نظر باشد یا این که بدانیم مقدار مورد جستجو در آرایه وجود ندارد تکرار می‌کنیم.

از روی مراحل فوق مشخص است که راه‌حل ما می‌تواند به صورت «بازگشتی» (recursive) باشد. ما در هر تکرار یک آرایه کوچک‌تر را به متد خود ارسال می‌کنیم تا این که تنها یک مقدار که مورد نظر ما است باقی بماند. بخش‌های دشوار این راه‌حل اندیس‌گذاری صحیح آرایه و ردگیری افست اندیس در هر تکرار است به طوری که بتوان اندیس مقدار مورد جستجو را در آرایه اصلی پیدا کرد. در کد زیر نسخه‌ای از الگوریتم جستجوی دودویی را مشاهده می‌کنید:

1def binary_search(arr, value, offset=0)
2  mid =  (arr.length) / 2
3  
4  if value < arr[mid] binary_search(arr[0...mid], value, offset) elsif value > arr[mid]
5     binary_search(arr[(mid + 1)..-1], value, offset + mid + 1)
6  
7  else
8     return offset + mid
9  end
10end

جستجوی دودویی پیچیدگی زمانی برابر با (O(logn دارد. می‌دانیم که در این حالت وقتی اندازه آرایه ورودی را دو برابر کنیم، باید یک تکرار بیشتر برای یافتن مقدار مطلوب در الگوریتم خود اضافه کنیم. به همین دلیل است که جستجوی باینری چنین الگوریتم کارآمدی در علوم رایانه محسوب می‌شود.

مرتب‌سازی ادغامی

«مرتب‌سازی ادغامی» (Merge Sort) از روش‌شناسی مشابه «تقسیم و حل» (divide and conquer) برای مرتب‌سازی کارآمد آرایه‌ها بهره می‌گیرد. مراحل زیر در مورد شیوه پیاده‌سازی مرتب‌سازی ادغامی است.

1. اگر آرایه تنها یک عنصر داشته باشد، بازگرد زیرا چنین آرایه‌ای مرتب محسوب می‌شود.
2. آرایه را به طور متوالی دو نیمه تقسیم کن، تا این که دیگر نتوان بیش از آن تقسیم کرد.
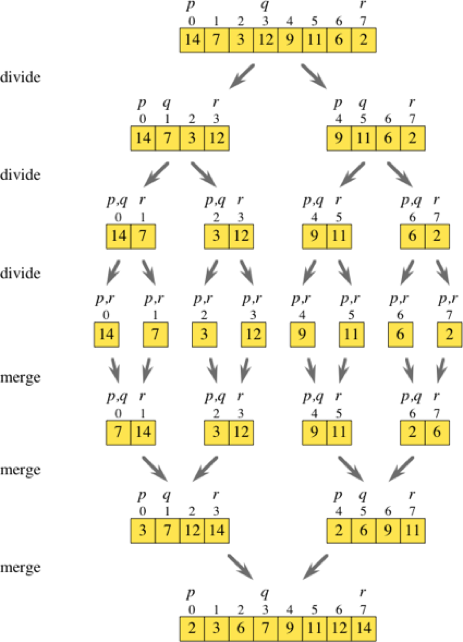
3. آرایه‌های کوچک‌تر را به صورت مرتب با هم ادغام کن تا این که به آرایه اصلی مرتب‌سازی شده برسی.

برای پیاده‌سازی مرتب‌سازی ادغامی، دو متد را تعریف خواهیم کرد. یکی از متدها اختصاص به افراز کردن آرایه دارد و دیگری وظیفه ادغام کردن مجدد دو آرایه مرتب را به صورت یک آرایه مرتب‌سازی شده بر عهده دارد. متد تقسیم کردن (merge_sort) به صورت بازگشتی فراخوانی می‌شود تا این که آرایه تنها یک عنصر طول داشته باشد. سپس این آرایه‌های فرعی با هم ترکیب می‌شوند تا نهایتاً یک آرایه مرتب بازگشت یابد. به مثال زیر توجه کنید:

1def merge_sort(array)
2  return array if array.length == 1
3  mid_point = array.length / 2
4  left = array[0...mid_point]
5  right = array[mid_point..-1]
6  merge(merge_sort(left), merge_sort(right))
7end
8def merge(left, right)
9    merged_arr = []
10    until left.empty? && right.empty?
11      if left.length == 0
12        merged_arr << right.shift
13      elsif right.length == 0
14        merged_arr << left.shift
15      elsif left[0] <= right[0]
16        merged_arr << left.shift
17      elsif right[0] <= left[0]
18        merged_arr << right.shift
19      end
20    end
21    merged_arr
22end

مرتب‌سازی ادغامی دارای پیچیدگی زمانی (O(nlog n است که بهترین پیچیدگی زمانی برای یک الگوریتم مرتب‌سازی محسوب می‌شود. ما می‌توانیم با بهره‌گیری از تقسیم و حل کردن، کارآیی مرتب‌سازی را که اصولاً یک پردازش پرهزینه از نظر محاسباتی است به میزان زیادی افزایش دهیم.

فیلم آموزش برنامه نویسی پایتون پیشرفته – ترفندهای Python در فرادرس

کلیک کنید

افزودن و حذف کردن آیتم از لیست پیوندی

لیست پیوندی یکی از ساختمان‌های داده بنیادی در علوم کامپیوتر محسوب می‌شود که دلیل آن به خاطر زمان ثابت درج و حذف است. با استفاده از گره‌ها و اشاره‌گرها می‌توانیم برخی پردازش‌ها را به روشی کارآمدتر از زمانی که از آرایه استفاده می‌کردیم اجرا کنیم. به نمودار شماتیک زیر توجه کنید:

یک لیست پیوندی از گره‌هایی تشکیل یافته است که هر یک بخشی از داده‌ها و یک اشاره‌گر به گره بعدی دارند. این وضعیت در Ruby با یک struct به نام Node نمایش پیدا می‌کند که دو آرگومان به نام‌های data: و:next_node دارد. اینک کافی است دو متد به نام‌های insert_node و delete_node تعریف کنیم که یک گره head و یک location برای مکانی که حذف/درج رخ می‌دهد می‌پذیرد.

متد insert_node یک آرگومان دیگر به نام node نیز دارد که همان struct گرهی است که می‌خواهیم درج کنیم. سپس حلقه‌ای تعریف می‌کنیم تا موقعیتی را که می‌خواهیم آیتمی را در آن درج یا حذف کنیم بیابیم. زمانی که به مکان مطلوب برسیم، اشاره‌گرها را طوری مجدداً چیدمان می‌کنیم تا عملیات درج/حذف ما را بازتاب دهند.

1Node = Struct.new(:data, :next_node)
2def insert_node(head, node, location)
3  current_node = head
4  current_location = 0
5  until current_location == location
6    previous_node = current_node
7    current_node = current_node.next_node
8    current_location += 1
9  end
10  if previous_node
11    previous_node.next_node = node
12    node.next_node = current_node
13  else
14    node.next_node = current_node
15  end
16  head
17end
18def delete_node(head, location)
19  current_node = head
20  current_location = 0
21  until current_location == location
22    previous_node = current_node
23    current_node = current_node.next_node
24    current_location += 1
25  end
26  if previous_node
27    previous_node.next_node = current_node.next_node
28  else
29    head = current_node.next_node
30  end
31  head
32end

در یک لیست پیوندی می‌توان آیتم‌ها را از میانه یک مجموعه بدون نیاز به تغییر دادن بقیه ساختمان داده در حافظه حذف کرد و این وضعیت کارایی بیشتری نسبت به ساختمان داده آرایه ‌ایجاد می‌کند. بدین ترتیب می‌بینیم که با انتخاب بهترین ساختمان داده بر اساس نیازها می‌توان به کارایی مناسبی دست یافت.

فیلم آموزش برنامه نویسی پایتون پیشرفته – ترفندهای Python در فرادرس

کلیک کنید

سخن پایانی

سه نسخه الگوریتمی که در این مقاله معرفی کردیم، تنها جزء کوچکی از الگوریتم‌های بنیادی هستند که باید برای خلق برنامه‌های کارآمد و موفقیت در مصاحبه‌های فنی بدانید. لیستی از الگوریتم‌های دیگر که در این زمینه توصیه می‌شود مطالعه کنید به شرح زیر هستند:

• الگوریتم Quicksort
• پیمایش یک درخت جستجوی دودویی
• درخت کمینه پوشا
• الگوریتم Heapsort
• معکوس سازی یک رشته به صورت درجا

البته مفاهیم دیگری نیز وجود دارند که باید بیاموزید، بنابراین توصیه می‌کنیم به تمرین کردن و درک مثال‌های بیشتری از الگوریتم‌ها ادامه بدهید.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌نویسی پایتون Python
• مجموعه آموزش‌های برنامه‌‌نویسی
• گنجینه آموزش های برنامه نویسی پایتون (Python)
• زبان برنامه نویسی پایتون (Python) — از صفر تا صد
• آموزش الگوهای طراحی (Design Patterns) در پایتون (Python)
• نحوه نوشتن الگوریتم – آموزش کامل و به زبان ساده

==