فشار چیست؟ – در فیزیک و به زبان ساده

فشار در فیزیک به صورت نسبت نیروی اعمال شده بر جسم بر مساحت سطح تماس، تعریف و رابطه آن به صورت $$\frac { F} { A}$$ نوشته می‌شود. پاسکال، واحد اصلی فشار در سیستم SI است. انواع مختلف فشار عبارت هستند از: فشار مطلق، فشار اتمسفر، فشار جزیی و فشار پیمانه‌ای. در این مطلب، ابتدا به پرسش فشار چیست به زبان ساده پاسخ می‌دهیم، سپس در مورد فشار در شاره‌ها، فشارسنج‌ها، انواع مختلف فشار و بالابر هیدرولیکی صحبت می‌کنیم. پس از خواندن این مطلب می‌دانیم: تعریف فشار چیست، واحد اندازه‌گیری فشار چیست، رابطه کلی فشار چیست، رابطه فشار در شاره‌ها چیست، فشار مطلق و پیمانه‌ای چیست و چه تفاوتی با یکدیگر دارند و بالابر هیدرولیک چیست.

فشار چیست ؟

هنگامی که می‌خواهید میخی را در دیوار فرو کنید از چکش کمک می‌گیرید. برای آن‌که میخ داخل دیوار قرار بگیرد، با استفاده از چکش بر قسمت مسطح میخ، نیرو وارد می‌کنید. قسمت تیز میخ که در تماس با دیوار قرار دارد، بر دیوار نیرو وارد می‌کند و در دیوار فرو می‌رود. اگر قسمت مسطح میخ را روی دیوار قرار دهید و با چکش بر قسمت تیز میخ ضربه وارد کنید، چه اتفاقی رخ می‌دهد؟ آیا میخ داخل دیوار فرو می‌رود؟ در این حالت، میخ داخل دیوار فرو نمی‌رود، حتی اگر با استفاده از چکش، ضربه‌های محکمی بر قسمت تیز میخ وارد کنیم.

آیا می‌دانید چرا این اتفاق رخ می‌دهد؟ دلیل این موضوع به کمیتی به نام فشار برمی‌گردد. فشار وارد شده بر دیوار از طرف نوک تیز میخ، بیشتر از فشار وارد شده از سمت مسطح آن است. چرا؟ به این نکته توجه داشته باشید که مساحت یا سطح مقطع قسمت تیز میخ، کمتر از مساحتِ قسمت مسطح آن است. به همین دلیل، مساحت سطحی که نیرو بر آن وارد می‌شود، بسیار مهم و تا‌ثیرگذار است. قبل از صحبت در مورد تاثیر مساحت، ابتدا فشار را تعریف می‌کنیم.

پس از پاسخ به پرسش فشار چیست، رابطه ریاضی آن را به‌دست می‌آوریم.

رابطه فشار چیست ؟

فشار برابر نسبتِ نیروی عمودی وارد شده بر سطح جسم بر مساحت سطح موردنظر است. تعریف فشار بسیار ساده به نظر می‌رسد، نیروی وارد شده بر واحد سطح. واحد نیرو در SI برابر نیوتن(N) و واحد سطح برابر مترمربع ($$m^ 2$$) است. بنابراین، واحد فشار در SI برابر $$\frac { N} { m^ 2 }$$ یا نیوتن بر متر مربع است. به واحد فشار، پاسکال (Pa)‌ نیز گفته می‌شود. چرا به واحد فشار پاسکال گفته می‌شود؟ نام پاسکال از نام دانشمندی فرانسوی به نام «بلز پاسکال» (Blaise Pascal) گرفته شده است.

$$P = \frac { F } { A }$$

به معادله نوشته شده برای فشار دقت کنید. مساحت در مخرج کسر قرار گرفته است. این مساحت، همان مساحتی است که نیرو بر آن وارد می‌شود. اگر نیروی وارد شده بر سطح ثابت باشد و مساحت سطح افزایش یابد، فشار چگونه تغییر می‌کند؟ بر طبق ریاضیات دبیرستان می‌دانیم هرگاه صورت کسر ثابت نگه داشته شود و مخرج کسر افزایش یابد، کل کسر کاهش خواهد یافت. بنابراین، با ثابت نگه‌ داشتن نیرو و افزایش سطح، فشار کاهش می‌یابد.

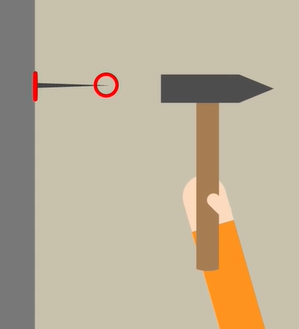
اجازه دهید بار دیگر به مثال چکش و میخ در ابتدای متن بازگردیم. نیروی وارد شده بر دیوار، بر سطح آن عمود و زاویه بین میخ و دیوار برابر ۹۰ درجه است. مساحت قسمت تیزِ میخ خیلی کمتر از مساحت قسمت مسطح آن است. بنابراین، سطح تماس قسمت تیز میخ و دیوار بسیار کمتر از سطح تماس قسمت مسطح آن با دیوار خواهد بود. در نتیجه، فشار وارد شده از سمت تیز میخ بیشتر از فشار وارد شده از سمت مسطح میخ است. به همین جهت، نوک تیز میخ بسیار راحت‌تر وارد دیوار می‌شود.

برای سوراخ کردن دیوار می‌توان از دریل نیز استفاده کرد. همان‌طور که در تصویر زیر مشاهده می‌شود، نوک دریل بسیار کوچک و تیز است. به همین دلیل، دیوار را به راحتی سوراخ می‌کند. برای بریدن میوه‌ها از قسمت تیز چاقو استفاده می‌کنیم. اگر برای بریدن میوه‌ها به جای لبه تیز چاقو، از لبه صاف آن استفاده کنیم، فرو کردن چاقو در میوه‌ها یا پوست کندن آن‌ها بسیار مشکل خواهد بود. آیا می‌دانید چرا؟ اگر به لبه‌های چاقو با دقت نگاه کنید، لبه تیز آن از نقطه‌های تیز و کوچکی به شکل مثلث تشکیل شده است.

لبه دیگر چاقو کاملا صاف است. بنابراین، اگر از لبه تیز چاقو برای بریدن میوه‌ها و خرد کردن سبزیجات استفاده کنیم، سطح تماس بین چاقو و سبزی یا میوه کاهش می‌یابد. از این‌رو، فشار بیشت

ری از سمت چاقو وارد می‌شود. برای قطع درختان از تبرهایی با لبه تیز استفاده می‌شود. دلیل این موضوع نیز به کاهش سطح تماس تبر با درخت و افزایش فشار وارد شده بر درخت، مربوط می‌شود. مثال‌هایی که تا اینجا بیان کردیم به ما نشان می‌دهد چگونه فشار زیاد می‌تواند برای پیشبرد کارهای روزمره مفید باشد.

اما سوالی که ممکن است مطرح شود آن است که آیا همیشه وارد کردن فشار زیاد برای انجام کارهای روزمره مفید است. در برخی موارد، فشار کم مزیت بیشتری نسبت به فشار زیاد دارد. برای راه رفتن روی برف از کفش‌های زمستانی با سطح تماس بزرگ استفاده می‌کنیم. بنابراین، به هنگام راه رفتن روی برف، فشار زیادی ایجاد نمی‌شود و داخل برف فرو نمی‌رویم. اگر هنگام راه رفتن روی برف از کفش‌های معمولی یا تابستانی استفاده کنیم، به دلیل سطح تماس کوچک‌تر و ایجاد فشار بزرگ‌تر، در برف فرو خواهیم رفت.

تا اینجا می‌دانیم فشار چیست و چه نقش مهمی در زندگی روزمره ایفا می‌کند، در ادامه می‌خواهیم بدانیم یکای فشار چیست.

یکای فشار چیست ؟

در مطالب بالا فشار را به صورت نسبت نیرو بر سطح تعریف کردیم:

$$P = \frac { F } { A }$$

رابطه بالا بدان معنا است که واحد فشار برابر نیوتن بر مترمربع خواهد بود. به نیوتن بر مترمربع، پاسکال نیز گفته می‌شود.

تا اینجا می‌دانیم فشار چیست و با رابطه کلی آن آشنا شدیم. قبل از حل مثال‌های مختلف توجه به این نکته مهم است که در رابطه داده شده برای فشار، سه نوع مسئله ممکن است مطرح شود:

1. مساحت و نیرو داده شده‌اند. در این صورت فشار وارد شده را از تقسیم نیرو بر مساحت به‌دست می‌آوریم.
2. مساحت و فشار داده شده‌اند. در این صورت نیروی وارد شده را از حاصل‌ضرب فشار در مساحت به‌دست می‌آوریم.
3. فشار و نیرو داده شده‌اند. در این صورت مساحت سطح را از تقسیم نیرو بر فشار به‌دست می‌آوریم.

برای داشتن درک بهتری از سه حالت بالا، به مثلث نشان داده شده در تصویر زیر توجه کنید. برای محاسبه هر یک از کمیت‌های خواسته شده می‌توان از این مثلث استفاده کرد. در این مثلت، خط افقی و عمودی رسم شده داخل مثلث به ترتیب نشان‌دهنده تقسیم و ضرب هستند. به عنوان مثال، برای به‌دست آوردن فشار، انگشت اشاره خود را روی $$P$$ قرار می‌دهیم. کمیت‌های باقی‌مانده نیرو و مساحت هستند که توسط خط افقی از یکدیگر جدا شده‌اند. بنابراین، برای محاسبه فشار، تنها کافی است نیروی وارد شده را بر مساحت سطح تقسیم کنیم.

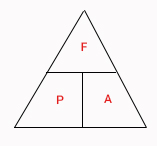
همچنین، اگر بخواهیم نیرو را به‌دست آوریم، تنها کافی است انگشت اشاره خود را روی $$F$$ قرار دهیم. کمیت‌های باقی‌مانده فشار و مساحت هستند که توسط خط عمودی از یکدیگر جدا شده‌اند. بنابراین، برای محاسبه نیرو، تنها کافی است فشار را در مساحت سطح ضرب کنیم.

تا اینجا با تعریف فشار آشنا شدیم و می‌دانیم یکا و رابطه فشار چیست. در ادامه، چند مثال در مورد چگونگی محاسبه فشار حل می‌کنیم.

مثال های محاسبه فشار

در ادامه و برای درک بهتر این مفهوم مثال‌هایی را با یکدیگر حل می‌کنیم.

مثال اول محاسبه فشار

نیرویی برابر ۱۵ نیوتن بر سطحی به مساحت ۰/۶ مترمربع اعمال می‌شود. فشار وارد شده بر سطح را به‌دست آورید.

پاسخ

در این مثال، با داشتن نیرو و مساحت سطح، باید فشار وارد شده را به‌دست آوریم. فشار با استفاده از رابطه زیر به‌دست می‌آید:

$$P = \frac { F } { A }$$

با قرار دادن نیرو و مساحت در رابطه بالا، داریم:

$$P = \frac { 15 N } { 0.6 m ^ 2 } = 25 \frac { N} { m ^ 2 } P = 25 Pa$$

مثال دوم محاسبه فشار

فشاری برابر ۵۰ پاسکال بر سطحی به مساحت ۵ مترمربع وارد می‌شود. مقدار نیروی F را به‌دست آورید.

پاسخ

در این مثال، با داشتن فشار و مساحت سطح، باید نیروی وارد شده را به‌دست آوریم. برای انجام این کار باید فشار را در مساحت ضرب کنیم:

$$F = P \times A = 50 Pa \times 5 m^ 2 F = 250 Pa.m ^ 2 = 250 N$$

مثال سوم محاسبه فشار

دانش‌آموزی به وزن ۶۰۰ نیوتن روی زمین ایستاده است. کفش‌های او در تماس با زمین قرار دارند و مساحت سطح تماس برابر ۰/۰۱۲ مترمربع است. فشار وارد شده از طرف دانش‌آموز بر زمین را به‌دست آورید.

پاسخ

در این مثال، نیروی وارد شده بر زمین همان نیروی وزن دانش‌آموز و برابر ۶۰۰ نیوتن است. با داشتن نیرو و مساحت سطح، باید فشار وارد شده را به‌دست آوریم. فشار با استفاده از رابطه زیر به‌دست می‌آید:

$$P = \frac { F } { A }$$

با قرار دادن نیرو و مساحت در رابطه بالا، داریم:

$$P = \frac { 600 N } { 0.012 m ^ 2 } = 5 \times 10 ^ 4 \frac { N} { m ^ 2 } P = 5 \times 10 ^ 4 Pa$$

مثال چهارم محاسبه فشار

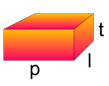
آجری به جرم ۳ کیلوگرم و به طول ۰/۳ متر ($$p =  0.3 m$$)، عرض ۰/۱۵ متر ($$0.15 m$$) و ارتفاع ۰/۱ متر ($$0.1 m$$) به صورت نشان داده شده در تصویر زیر روی میز قرار داده شده است. فشار وارد شده از طرف آجر بر میز را به‌دست آورید.

پاسخ

برای محاسبه فشار، باید نیروی وارد شده از طرف آجر بر میز و مساحتِ در تماس با میز را محاسبه کنیم. ابتدا، مساحت تماس را به‌دست آوریم. آجر، مکعب مستطیلی با ۶ وجه که دو به دو با یکدیگر برابر هستند:

• دو وجه با مساحتی برابر $$A = p \times l$$
• دو وجه با مساحتی برابر $$A = l \times t$$
• دو وجه با مساحتی برابر $$A = p \times t$$

آجر از سطح $$p \times l$$ روی میز قرار گرفته است، بنابراین مساحت سطح برابر است با:

$$A = p \times l A = 0. 3 \times 0.15 =  0.045 m ^ 2$$

نیروی وارد شده از طرف آجر بر میز همان نیروی وزن و برابر است با:

$$F = W = m g = 3 \times 10 = 30 N$$

بنابراین، فشار وارد شده بر میز از سمت آجر برابر است با:

$$P = \frac { F } { A } P = \frac { 30 } { 0.045} = 666.7 Pa$$

مثال پنجم محاسبه فشار

دختری به وزن ۶۰ کیلوگرم، کفش‌های پاشنه بلند پوشیده است و سعی دارد تعادل خود را روی یک پاشنه حفظ کند. اگر پاشنه کفش او دایره‌ای کوچک به قطر ۱/۵ سانتی‌متر باشد، فشار وارد شده از طرف پاشنه بر کف اتاق را به‌دست آورید.

پاسخ

داده‌های مثال عبارت هستند از:

• جرم که برابر ۶۰ کیلوگرم است.
• قطر پاشنه برابر ۱/۵ سانتی‌متر است، بنابراین شعاع آن برابر $$r = \frac { 1.5 \times 10 ^ -2 } { 2 }$$ خواهد بود.

نیروی وارد شده از سمت دختر برابر $$F = mg$$ است. همچنین، مساحت سطح تماس پاشنه با کف اتاق برابر $$A = \pi r ^ 2$$ خواهد بود. فشار وارد شده از طرف پاشنه بر کف اتاق برابر است با:

$$P = \frac { mg } { \pi r ^ 2 } = \frac { 60 \times 9.8 } { 3.142 \times ( 0.75 \times 10 ^ { -2 } ) ^ 2} P = 3.32 \times 10 ^ 6 Pa$$

مثال ششم محاسبه فشار

مثال هفتم محاسبه فشار

مثال هشتم محاسبه فشار

پس از پاسخ به پرسش فشار چیست و صحبت در مورد فشار وارد شده از طرف اجسام جامد بر سطحی مشخص، در مورد فشار در شاره‌ها (سیالات یا مایعات) صحبت می‌کنیم.

فشار در شاره ها

بیشتر دانش‌آموزان دبیرستان به هنگام پاسخ به پرسش فشار چیست، به فشار در شاره‌ها فکر می‌کنند. در این بخش، رابطه فشار در شاره‌ها را به‌دست می‌آوریم. قبل از توضیح در مورد فشار در شاره‌ها یا سیالات، ابتدا کمی در مورد شاره (سیال) صحبت می‌کنیم. سیال، شکل مشخصی ندارد و شکل ظرفی که در آن ریخته شده است را به خود می‌گیرد. فرض کنید ظرفی شیشه‌ای به شکل کره داریم و آن را به طور کامل با آب پر می‌کنیم. در این حالت، آب به شکل ظرف شیشه‌ای کروی درمی‌آید. اگر آبِ داخل ظرف کروی را به داخل ظرف دیگری با شکلی نامشخص و حجم یکسان منتقل کنیم، آب به شکل ظرف جدید درمی‌آید.

شاره‌ها به دو قسمت تقسیم می‌شوند:

• مایعات
• گازها

گازها و مایعات، شکل ظرفی که در آن قرار دارند را به خود می‌گیرند. سوالی که ممکن است مطرح شود آن است که فرق مایع و گاز چیست. گازها، تراکم‌پذیر هستند، اما مایعات تراکم‌پذیر نیستند. ظرفی شیشه‌ای به شکل U در تصویر زیر نشان داده شده است. همان‌طور که در تصویر دیده می‌شود سطح مقطع سرهای بازِ ظرف برابر نیستند. این ظرف را با مایعی مانند آب یا هر مایع دیگری پر می‌کنیم.

کار برابر حاصل‌ضرب نیرو در جابجایی است:

$$W = F . D$$

کار وارد شده به سیستم برابر کار خارج شده از آن است. این بیان، قانون پایستگی انرژی را نشان می‌دهد.

$$W _ { \in } = W _ { out } F_ { \in } D _ { i n } = F _ { out } D _ { out }$$

فرض کنید در ستون سمت چپ، پیستونی قرار می‌دهیم و آن را با نیروی F به اندازه $$d_1$$ به سمت پایین فشار می‌دهیم. سوالی که می‌خواهیم به آن جواب دهیم آن است که چه مقدار آب جابجا می‌شود. پیستون به اندازه $$d_1$$ به سمت پایین حرکت کرده است. برای آن‌که بدانیم چه مقدار آب جابجا شده است باید حجم استوانه‌ای به ارتفاع $$d_1$$ و سطح $$A_ 1$$ را به‌دست آوریم.

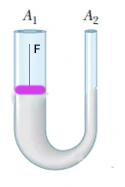
این حجم برابر است با :

$$V_ 1 = A_1 \times d_1$$

از آنجا که مایعات تراکم‌ناپذیر هستند، مایع جابجا شده در اثر فشار پیستون باید به مکان دیگری منتقل شده باشد. با فشار پیستون و کاهش ارتفاع مایع در ستون سمت چپ، ارتفاع مایع در ستون سمت راست افزایش می‌یابد. بنابراین، مایع جابجا شده در اثر فشار پیستون سبب افزایش ارتفاع مایع در ستون سمت راست ظرف می‌شود. فرض کنید ارتفاع مایع در ستون سمت راست به اندازه $$d_2$$ افزایش می‌یابد. از آنجا که سطح مقطع ستون‌ها با یکدیگر برابر نیستند، ارتفاع $$d_1$$ نیز با ارتفاع $$d_2$$ برابر نیست.

حجم مایع جابجا شده در ستون سمت راست برابر حجم استوانه‌ای به ارتفاع $$d_2$$ و مساحت $$A_2$$ است:

$$V_ 2 = A_2 \times d_2$$

از آنجا که مایع تراکم‌ناپذیر است، حجم‌های $$V_1$$ و $$V_2$$ با یکدیگر برابر هستند:

$$V_ 1 = V _ 2 A_1 d _1 = A_2 d _ 2$$

در مطالب بالا گفتیم بر طبق اصل پایستگی انرژی، کار یا انرژی وارد شده به سیستم برابر انرژی یا کار خارج شده از سیستم است. در ابتدا پیستونی را در ستون سمت چپ تعبیه کردیم و آن را با نیروی $$F_1$$ به سمت پایین فشار دادیم. بنابراین، ارتفاع مایع در این ستون به اندازه $$d_1$$، کاهش می‌یابد. از آنجا که مایعات تراکم‌ناپذیر هستند، مایع در ستون سمت راست به اندازه $$d_2$$ بالا می‌رود به گونه‌ای که حجم‌های $$V_1$$ و $$V_2$$ با یکدیگر برابر می‌شوند.

پیستونی را در ستون سمت راست، به شکل زیر قرار می‌دهیم و فرض می‌‌کنیم با نیروی $$F_2$$ به سمت بالا هل داده می‌شود.

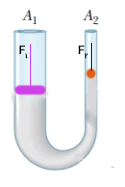
بر طبق اصل پایستگی انرژی داریم:

$$W _ { \in } = W _ { out } F_ { \in } D _ { i n } = F _ { out } D _ { out }$$

سمت چپ و راست رابطه بالا را به ترتیب در $$A_1$$ و $$A_2$$ ضرب و بر $$A_1$$ و $$A_2$$ تقسیم می‌کنیم.

$$\frac { F_ 1 } { A _ 1 } A _ 1 d_ 1 = \frac { F _2 } { A _ 2 } A_ 2 d _ 2$$

کسرهای $$\frac { F_ 1 } { A _ 1 }$$ و $$\frac { F_ 1 } { A _ 1 }$$ چه کمیتی را نشان می‌دهند؟ در مطالب بالا فشار را به صورت نیرو بر سطح تماس تعریف کردیم. بنابراین، این دو کسر فشار را نشان می‌دهند. همچنین حاصل‌ضرب مساحت در جابجایی، حجم مایع جابجا شده در ستون‌ها را بیان می‌کند. بنابراین، رابطه بالا به شکل زیر نوشته می‌شود:

$$P _1 V_ 1  = P _ 2 V _ 2$$

حجم‌های $$V_1$$ و $$V_ 2$$ با یکدیگر برابر هستند، بنابراین به راحتی از طرفین تساوی $$P _1 V_ 1  = P _ 2 V _ 2$$ ساده می‌شوند. در نتیجه، داریم:

$$P _ 1 = P _2$$

به بیان دیگر، فشاری که از سمت بیرون به سیستم وارد می‌شود برابر فشاری است که از سمت سیستم به محیط اطراف وارد می‌شود. به بیان دیگر، هر فشاری به سیستم از سمت محیط اطراف وارد شود، به طور مساوی و یکنواخت در سراسر آن توزیع خواهد شد. این تعریف به عنوان اصل پاسکال شناخته می‌شود.

در مطلب بالا به پرسش‌های فشار چیست، رابطه و یکای فشار چیست پاسخ دادیم و در مورد فشار در شاره‌ها صحبت کردیم. در ادامه، فشار در عمق مشخصی از سیال را به‌دست می‌آوریم.

فشار در عمق سیال

در مطالب بالا گفتیم هر فشار خارجی وارد شده بر مایع در محفظه، در سراسر آن به صورت یکنواخت توزیع می‌شود. توزیع یکنواخت فشار خارجی در سراسر مایع، اصل پاسکال نامیده می‌شود. اصل پاسکال، تنها برای فشار خارج از مایع به کار برده می‌شود. سوالی که ممکن است مطرح شود آن است که فشار داخل مایع چگونه تغییر می‌کند. آیا تا به حال از ارتفاع مشخصی به داخل استخر شیرجه زده‌اید؟

اگر این کار را انجام داده باشید، به طور حتم متوجه شده‌اید که هرچه در عمق بیشتری از آب فرو می‌روید، فشار بیشتری بر شما وارد می‌شود. اجازه دهید تغییرات فشار داخلی مایع با ارتفاع از سطح آن را با دقت بیشتری بررسی کنیم. استوانه‌ای با ارتفاع مشخص را به صورت نشان داده شده در تصویر زیر در نظر بگیرید که توسط مایعی دلخواه پر شده است. فرض کنید این استوانه در سیاره‌ای بدون اتمسفر و با جرمی برابر با جرم زمین قرار دارد. بنابراین، محیط اطراف استوانه خلأ است.

حجم بسیار کوچکی را داخل مایع و در عمق h از سطح، به صورت نشان داده شده در تصویر انتخاب می‌کنیم. دلیل این انتخاب آن است که بدانیم آیا مایع حرکت می‌کند یا خیر. از آنجا که مایع به طور کامل ساکن است، حجم کوچک انتخاب شده نیز ساکن باقی می‌ماند. از قوانین نیوتن می‌دانیم برای آن‌که جسمی ساکن بماند، برایند نیروهای وارد شده بر آن باید برابر صفر باشد. این حالت برای حجم انتخاب شده در عمق h نیز صدق می‌کند. بنابراین، برایند نیروهای وارد شده بر آن باید برابر صفر باشد، $$F_ { up } = F _ { down }$$.

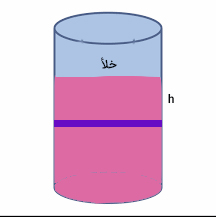
سوالی که ممکن است مطرح شود آن است که نیروهای رو به پایین و رو به بالای وارد شده بر حجم انتخابی درون مایع چه نیروهایی هستند؟ $$F_ { down}$$ برابر نیروی وزن مقدار مایع قرار گرفته بالای حجم انتخاب شده است. اگر جرم مایع قرار گرفته بالای حجم موردنظر برابر $$m_ l$$ باشد، $$F_ { down}$$ برابر است با:

$$F _ { Down} = m _ l . g$$

$$m _ 1$$ چه مقدار است؟ برای به‌دست آوردن $$F_ { down}$$ باید مقدار $$m _ 1$$ را محاسبه کنیم. برای انجام این کار باید از کمیتی به نام چگالی استفاده کنیم. به مقدار ماده قرار گرفته در حجمی مشخص، چگالی گفته می‌شود و به صورت زیر نوشته می‌شود.

$$\rho = \frac { m } { V}$$

واحد اندازه‌گیری چگالی، کیلوگرم بر مترمکعب است. با توجه به رابطه نوشته شده برای چگالی، $$m_l$$ را می‌توان به صورت زیر نوشت:

$$m_ l = \rho _ l . V _ l$$

با قرار دادن رابطه بالا در فرمول $$F _ { Down} = m _ l . g$$ داریم:

$$F _ { Down} = m_ l = \rho _ l . V _ l . g$$

در مرحله بعد باید $$V_ l$$ را به‌دست آوریم. این حجم برابر حاصل‌ضرب مساحت سطح مقطع استوانه در ارتفاع h است. اگر مساحت سطح مقطع استوانه برابر A باشد، $$V_ l$$ برابر با $$A h$$ خواهد بود. در نتیجه، نیروی $$F _ { down}$$ به صورت زیر نوشته می‌شود:

$$F _ { down } = \rho _ l . h . A . g$$

تا اینجا، مقدار نیروی $$F _ { down }$$ وارد شده بر حجم انتخاب شده در مایع را به‌دست آوردیم. در ادامه، فشار وارد شده بر حجم موردنظر را محاسبه می‌کنیم. همان‌طور که در مطالب بالا گفتیم فشار برابر نسبت نیرو بر مساحت سطح تماس است:

$$P = \frac { F } { A}$$

بنابراین، فشار وارد شده بر حجم انتخابی درون مایع برابر است با:

$$P _ { down } = \frac { F _ { down }} { A} = \frac { \rho h A g } { A} P _ { down} = \rho h g$$

از آنجا که نیروی رو به پایین با نیروی رو بالا با یکدیگر برابر هستند، فشارهای رو به پایین و رو به بالا نیز با یکدیگر برابر خواهند بود. اگر مایع موردنظر آب باشد، چگالی برابر ۱۰۰۰ کیلوگرم بر مترمکعب است. فشار در عمق ۱۰ متری از سطح آب چه مقدار است؟ برای محاسبه فشار در عمق ۱۰ متری از سطح آب از رابطه $$P = \rho g h$$ استفاده می‌کنیم:

$$P = \rho g h P = 1000 \times 10 \times 10 P = 10 ^ 5 Pa$$

این فشار برابر فشار یک اتمسفر است. برای محاسبه فرمول فشار مایع در عمق مشخصی از آن، فشار جو را در نظر نگرفتیم و محیط اطراف مایع را خلأ در نظر گرفتیم. سوالی که به طور حتم برای شما مطرح می‌شود آن است که اگر محیط اطراف مایع خلأ نباشد، چه کاری باید انجام داد؟ هوا در همه جا وجود دارد. با در نظر گرفتن هوای بالای مایع، فشار کل یا فشار مطلق در ارتفاع h از سطح آن برابر است با:

$$P _ { total}  = \rho g h + P _ { at m }$$

چرا به جای $$P _ { at m }$$ از رابطه $$\rho _ { air } g h$$ استفاده نمی‌کنیم؟ دلیل این موضوع آن است که عمق ما در جو زمین برای هر اندازه‌گیری به طور تقریب ثابت در نظر گرفته می‌شود. این بدان معنا است که فشار اتمسفر در سطح زمین تقریبا ثابت در نظر گرفته می‌شود. مقدار این فشار در سطح زمین در حدود $$1.01 \times 10 ^ 5 Ps$$ است. به دلیل الگوهای آب‌و‌هوایی، این عدد ممکن است نوسان داشته باشد. اما در حل مسئله‌های فیزیک مقدار آن را یکسان و برابر مقدار داده شده در نظر می‌گیریم.

$$P _ { total}  = \rho g h + 1.01 \times 10 ^ 5 Pa$$

برای پاسخ به پرسش فشار چیست، تنها تعریف فشار و آشنایی با رابطه کلی آن کافی نیست. بلکه باید بدانیم انواع فشار چیست و چه تفاوتی با یکدیگر دارند.

تفاوت فشار مطلق و فشار پیمانه ای چیست ؟

در بیشتر موارد به هنگام اندازه‌گیری فشار، مقدار فشار کل مهم نیست. در واقع، اختلاف فشار با فشار اتمسفر مهم است. دلیل این موضوع آن است که فشار اتمسفر مقداری ثابت روی سطح زمین در نظر گرفته می‌شود و همواره وجود دارد. بنابراین، گاهی مواقع در نظر گرفتن آن در محاسبات کاری بیهوده به نظر می‌رسد. به همین دلیل،‌ بیشتر تجهیزات گیج و نظارتی از فشاری به نام فشار پیمانه‌ای استفاده می‌کنند. به فشار اندازه‌گیری شده نسبت به فشار اتمسفر یا فشار جو، فشار پیمانه‌ای گفته می‌شود.

فشار پیمانه‌ای می‌تواند:

• برای فشارهایی بالاتر از فشار جو، مثبت باشد.
• برای فشارهایی برابر فشار جو، صفر باشد.
• برای فشارهایی پایین‌تر از فشار جو، منفی باشد.

به فشار کل (شامل فشار جو)، فشار مطلق گفته می‌شود. به بیان دیگر، فشار مطلق، فشار را نسبت به خلأ مطلق اندازه می‌گیرد. بنابراین، مقدار آن برای تمام فشارهای بالاتر از خلأ مطلق مثبت و برای خلأ مطلق برابر صفر است. مقدار فشار مطلق هرگز نمی‌تواند منفی باشد. فشار مطلق برابر حاصل جمع فشار پیمانه‌ای و فشار اتمسفر است:

$$P _ {absolute} = P _ {gauge} + P _ { atm}$$

برای به‌دست آوردن فشار در عمق h برای مایعی ساکن و در تماس با هوا در نزدیکی سطح زمین، فشار پیمانه‌ای و فشار مطلق به صورت زیر نوشته می‌شوند:

$$P _ { gauge} = \rho g h P _ { absolute} = \rho g h + 1.01 \times 10 ^ 5 Pa$$

برای آشنایی بیشتر با فشار پیمانه‌ای و مطلق و تفاوت آن‌ها، چند مثال را با یکدیگر حل می‌کنیم.

مثال اول فشار مطلق و فشار پیمانه‌ای

فشار داخلی مخزنی در سطح دریا برابر ۴.۲ اتمسفر است. مقدار فشار پیمانه‌ای داخل مخزن را به‌دست آورید.

پاسخ

فشار پیمانه‌ای با استفاده از رابطه زیر به‌دست می‌آید:

$$P_ {gauge} = P_ {total} - P _ {atm}$$

به فشار اندازه‌گیری شده نسبت به فشار اتمسفر، فشار پیمانه‌ای گفته می‌شود. با توجه به مثال داده شده، فشار کل داخل مخزن برابر ۴/۲ اتمسفر است، بنابراین فشار پیمانه‌ای برابر است با:

$$P _ {gauge} = 4.2 - 1 = 3.2 atm$$

مثال دوم فشار مطلق و فشار پیمانه‌ای

فشار داخلی مخزنی در سطح دریا برابر ۰/۹ اتمسفر است. مقدار فشار پیمانه‌ای داخل مخزن را به‌دست آورید.

پاسخ

فشار پیمانه‌ای با استفاده از رابطه زیر به‌دست می‌آید:

$$P_ {gauge} = P_ {total} - P _ {atm}$$

با توجه به مثال داده شده، فشار کل داخل مخزن برابر ۰/۹ اتمسفر است، بنابراین فشار پیمانه‌ای برابر است با:

$$P _ {gauge} = 0.9 - 1 = - 0.1 atm$$

مثال سوم فشار مطلق و فشار پیمانه‌ای

غواصی در عمق ۵۰ متری اقیانوس قرار دارد.

1. فشار پیمانه‌ای در این نقطه چه مقدار است؟
2. فشار مطلق را به‌دست آورید. (چگالی آب دریا برابر ۱۰۲۵کیلوگرم بر مترمکعب است)

پاسخ

غواص در عمق ۵۰ متری اقیانوس قرار دارد. ابتدا فشار پیمانه‌ای را به‌دست می‌آوریم. فشار در حالت کلی با استفاده از رابطه زیر به‌دست می‌آید:

$$P= \frac { F} { A}$$

در قسمت اول می‌خواهیم فشار پیمانه‌ای ناشی از آب اقیانوس را به‌دست آوریم. برای به‌دست آوردن این فشار از رابطه بالا استفاده می‌کنیم. برای انجام این کار باید نیروی حاصل از تمام مولکول‌های آبِ بالای غواص را بر مساحت غواص تقسیم کنیم. نیروی وارد شده از طرف مولکول‌های آبِ قرار گرفته بالاتر از غواص همان نیروی وزن کل آبِ بالای سر غواص است.

$$F = mg$$

از آنجا که آب، سیال است، به طور مستقیم از جرم برای محاسبه وزن استفاده نمی‌کنیم، بلکه از رابطه زیر جرم را برحسب چگالی و حجم می‌نویسیم:

$$\rho = \frac { m } { \rho } m = \rho V$$

رابطه به‌دست آمده برای جرم را در رابطه فشار پیمانه‌ای قرار می‌دهیم:

$$P_G = \frac { \rho V g } { A}$$

حجم از حاصل‌ضرب مساحت در ارتفاع به‌دست می‌آید:

$$P_G = \frac { \rho A h g } { A}$$

با ساده کردن A از صورت و مخرج رابطه بالا، فشار پیمانه‌ای به صورت زیر نوشته می‌شود:

$$P_G = \rho h g$$

مقدارهای داده شده را در رابطه بالا قرار می‌دهیم:

$$P_G = 1025 (9.8) (50) P _ G = 502250 Pa$$

فشار مطلق در نقطه‌ای که غواص قرار دارد برابر مجموع فشار اتمسفر و فشار ناشی از وزن آب بالای غواص است.

$$P _ { total } = P _ G + P _ { atm} P _ T = 502250 + 101323 603550 Pa$$

مثال چهارم فشار مطلق و فشار پیمانه‌ای

در تصویر نشان داده شده در ادامه، ارتفاع آب و نفت به ترتیب برابر ۲۵ متر و ۸ متر است. محفظه، باز و در معرض هوا قرار دارد. مطلوب است:

1. فشار مطلق و فشار پیمانه‌ای در مرز بین آب و نفت.
2. فشار مطلق و فشار پیمانه‌ای در کف محفظه.

چگالی نفت برابر ۷۵۰ کیلوگرم بر مترمکعب است.

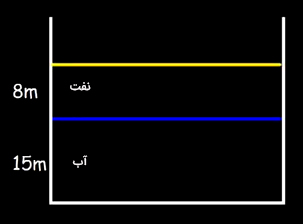
پاسخ

ابتدا فشار مطلق و پیمانه‌ای را در مرز آب و نفت به‌دست می‌آوریم. فشار پیمانه‌‌ای در این نقطه برابر است با:

$$P _ { G \, oil} = \rho _ { oil} g h = 750 \times 9.8 \times 8 = 58800 Pa$$

فشار مطلق برابر مجموع فشار پیمانه‌ای و فشار جو است:

$$P _ {total} = P _ { G \, oil} + P _ {atm} = 58800+ 101325 = 160125 Pa$$

در ادامه، فشار مطلق و پیمانه‌ای را در کف محفظه به‌دست می‌آوریم. فشار پیمانه‌‌ای در این نقطه برابر است با:

$$P _ { G } = P_ {oil } + P_ { water} = \rho _ { oil} g h_{ oil } + \rho _ { water } g h _ { water}  = 750 \times 9.8 \times 8 + 1000 \times 9.8 \times 15 = 205800 Pa$$

فشار مطلق برابر مجموع فشار پیمانه‌ای و فشار جو است:

$$P _ {total} = P _ { G \, oil} + P _ {atm} =  205800 + 101325 = 307100 Pa$$

تاکنون می‌دانیم انواع فشار چیست و چه تفاوتی با یکدیگر دارند. علاوه بر فشارهای مطلق و پیمانه‌ای، نوع دیگری از فشار به نام فشار جزیی نیز وجود دارد که در ادامه، در مورد آن صحبت خواهیم کرد.

محاسبه ارتفاع مایع در فشارسنج

تا اینجا می‌دانیم:

• فشار چیست.
• یکای فشار چیست.
• رابطه کلی فشار چیست.
• انواع فشار چیست.
• اصل پاسکال در مبحث فشار چیست.
• فشار در عمق مشخصی از سطح مایع چگونه به‌دست می‌آید.

در ادامه، ارتفاع مایع را در فشارسنج به‌دست می‌آوریم. ظرفی را در نظر بگیرید که با جیوه پر شده است. لوله‌ آزمایشگاهی را برمی‌داریم و آن را به صورت وارونه درون ظرف حاوی جیوه فرو می‌کنیم. لوله آزمایشگاه را به گونه‌ای درون جیوه فرو می‌بریم که هیچ هوایی درون آن باقی نماند. بنابراین، محیط درون لوله را خلأ در نظر می‌گیریم. محیط اطراف لوله خلأ نیست. همچنین، فرض می‌کنیم ظرف حاوی جیوه و لوله درون آن در سطح دریا قرار دارند.

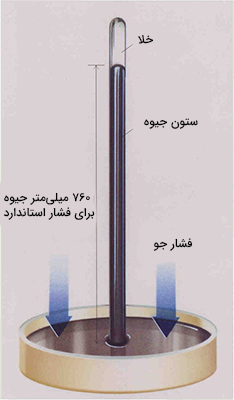
از آنجا که آزمایش را در سطح دریا و در فشاری برابر یک اتمسفر انجام می‌دهیم، فشار هوای وارد شده بر جیوه برابر یک اتمسفر خواهد بود. از آنجا که داخل لوله خلأ است و هیچ فشاری در آنجا وجود ندارد و به دلیل آن‌که فشار محیط اطراف بیشتر از فشار داخل لوله است، جیوه تا ارتفاع مشخصی داخل لوله بالا می‌رود. در ادامه، می‌خواهیم ارتفاع جیوه در لوله را به‌دست آوریم. برای انجام این کار به نکته زیر توجه کنید:

• چگالی نسبی جیوه برابر ۱۳/۶ است. به نسبت چگالی ماده‌ای مشخص به ماده مرجع، چگالی نسبی گفته می‌شود. چگالی نسبی جیوه نسبت به آب سنجیده می‌شود. این بدان معنا است که جیوه ۱۳/۶ چگال‌تر از آب است. از آنجا که چگالی آب برابر ۱۰۰۰ کیلوگرم بر سانتی‌متر مکعب است، چگالی جیوه برابر $$13.6 \times 1000$$ کیلوگرم بر سانتی‌متر مکعب خواهد بود.

برای محاسبه ارتفاع جیوه در لوله آزمایش، کف لوله و محل ورود آن به داخل جیوه را در نظر بگیرید (خط قرمز در تصویر نشان داده شده در ادامه).

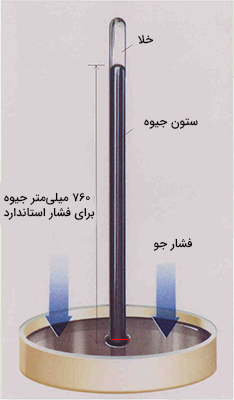
در مطالب بالا آموختیم فشار وارد شده به سیستم برابر فشار خروجی از آن است. از آنجا که فشار وارد شده به سیستم (جیوه) از طرف محیط اطراف برابر یک اتمسفر است، فشار وارد شده بر محل تلاقی لوله و سطح جیوه (فشار به سمت بالا) نیز برابر یک اتمسفر خواهد بود. می‌دانیم فشار به سمت بالا در نقطه موردنظر برابر فشار به سمت پایین در این نقطه است. در نتیجه، فشار به سمت پایین نیز برابر یک اتمسفر خواهد بود.

مقدار فشار رو به پایین برابر است با:

$$P = \rho g h$$

بنابراین، حاصل‌ضرب چگالی جیوه، ارتفاع آن و شتاب جاذبه زمین در یکدیگر برابر یک اتمسفر خواهد بود:

$$13600 \frac { k g } { m ^ 3 } \times h \times 9.8 \frac { m } { s ^ 2 } = 103000 Ps h = \frac { 103000 \frac Pa } { 13600 \frac {kg } { m ^ 3 } \times 9.8 \frac { m} { s ^ 2 } } h = 0.77 m h = 77.2 cm$$

تا اینجا یکای فشار را برحسب پاسکال بیان کردیم. میلی‌متر جیوه یکای رایج دیگری برای اندازه‌گیری فشار است. در ادامه، در مورد این واحد و چگونگی تبدیل یکای پاسکال به آن صحبت می‌کنیم.

واحد میلی متر جیوه در اندازه گیری فشار چیست ؟

mmHg یا میلی‌متر جیوه محاسبات بسیار مهمی در فیزیک و یکی از واحدهای اندازه‌گیری فشار در واحد «مانومتریک» (manometric) است. یک میلی‌متر جیوه برابر ۱۳۳/۳۲۲ پاسکال است. یک میلی‌متر جیوه مقدار فشاری است که توسط یک میلی‌متر جیوه در ستون عمودی در دمای صفر درجه سلسیوس وارد می‌شود. از آنجا که یک میلی‌متر جیوه برابر ۱۳۳/۳۲۲ پاسکال است، فشار یک اتمسفر نیز در حدود ۷۶۰ میلی‌متر جیوه خواهد بود.

مثال تبدیل میلی‌متر جیوه به پاسکال

اگر فشار خون برابر ۱۲۰ میلی‌متر جیوه باشد، مقدار آن را برحسب پاسکال به‌دست آورید.

پاسخ

فشار وارد شده از طرف جیوه در ستون عمودی بارومتر برابر است با:

$$P = \rho _ { Hg } g h$$

در رابطه فوق، h ارتفاع جیوه در لوله عمودی بارومتر است. چگالی جیوه برابر ۱۳۶۰۰ کیلوگرم بر مترمکعب، شتاب جاذبه زمین برابر ۹/۸ متر بر مجذور ثانیه است. ارتفاع جیوه چه مقدار است؟ فشار خون برابر ۱۲۰ میلی‌متر جیوه است، بنابراین ارتفاع جیوه برابر ۱۲۰ میلی‌متر یا ۰/۱۲ متر خواهد بود. با قرار دادن مقدارهای داده شده در رابطه بالا، فشار خون را برحسب پاسکال به‌دست می‌آوریم:

$$P = 136000 (9.8) ( 0.12) = 15993.6 Pa$$

گفتیم فشار یک اتمسفر برابر ۷۶۰ میلی‌متر جیوه و یک اتمسفر نیز برابر ۱۰۱۳۲۵ پاسکال است. بنابراین، داریم:

$$101325 Pa = 760 mmHg$$

طرفین رابطه بالا را در $$\frac { 1 } { 760 }$$ ضرب می‌کنیم:

$$1 mmHg = 1 Pa \times \frac { 101325 } { 760 }$$

با ساده کردن سمت راست رابطه بالا داریم:

$$1 mmHg = Pa \times 0.0075$$

به عنوان مثال، اگر بخواهیم فشاری برابر ۳۶۰۰۰ پاسکال را برحسب میلی‌متر جیوه به‌دست آوریم، به صورت زیر عمل می‌کنیم:

$$P = 36000 \times 0.0075 = 270.02 mmHg$$

تا اینجا می‌دانیم فشار چیست و با استفاده از چه رابطه‌ای به‌دست می‌آید. همچنین، با فشار در شاره‌ها، محاسبه فشار در عمق مشخصی از مایعات، تفاوت فشار پیمانه‌ای و مطلق و محاسبه ارتفاع مایع در فشارسنج آشنا شدیم. در ادامه مثال‌هایی در مورد فشارسنج‌های مانومتر حل می‌کنیم.

فشارسنج شاره ها (مانومتر)

فشار گاز در محفظه بسته در همه جا یکسان است. «مانومتر» (Manometer) برای اندازه‌گیری فشار گاز در محفظه بسته مورد استفاده قرار می‌گیرند. دو نوع مانومتر وجود دارد. مانومتر یا فشارسنج به شکل U هستند و به طور معمول توسط جیوه پر شده‌اند. اگر یکی از لوله‌های مانومتر باز و در معرض هوا باشد، به آن مانومتر نوع باز گفته می‌شود. اگر دو انتها بسته باشند، به آن مانومتر بسته می‌گوییم.

مانومتر بسته

همان‌طور که در تصویر زیر دیده می‌شود، یک انتهای مانومتر به محفظه حاوی گاز متصل و انتهای دیگر آن نیز بسته است. نقطه‌های $$x$$ و $$y$$ هم‌تراز هستند، بنابراین فشار وارد شده بر این دو نقطه با یکدیگر برابر خواهند بود. فشار در نقطه $$x$$ برابر فشار گاز و فشار در نقطه $$y$$ برابر فشار وارد شده از طرف وزن جیوه است.

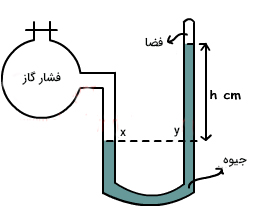
در این سیستم فشار گاز با استفاده از رابطه زیر به‌دست می‌آید:

$$P_ {gas} = \rho g h$$

اثبات: همان‌طور که گفتیم نقطه‌های $$x$$ و $$y$$ هم‌تراز هستند، بنابراین فشار وارد شده در این دو نقطه با یکدیگر برابر هستند:

$$P _ x = P _ y$$

فشار در نقطه $$x$$ برابر فشار گاز و فشار در نقطه $$y$$ برابر فشار وارد شده از طرف وزن جیوه است:

$$P _ {gas} = rho_ { mercury} g h$$

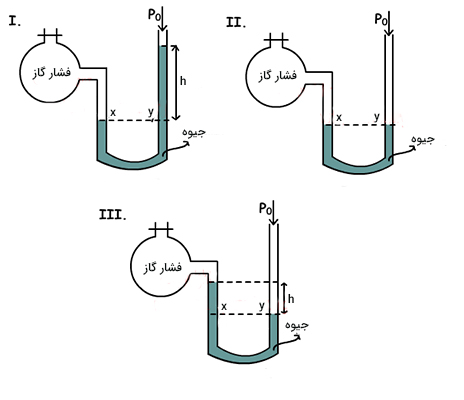
مانومتر لوله باز

همان‌طور که در تصویر زیر دیده می‌شود، یک انتهای مانومتر به محفظه حاوی گاز متصل و انتهای دیگر آن در معرض فشار هوا قرار دارد.

در مطالب بالا گفتیم نقش فشارسنج در تعیین مقدار فشار چیست. در ادامه، این وسیله را با حل چند مثال توضیح می‌دهیم.

حل مثال مانومتر لوله باز

در ادامه، چند مثال در مورد مانومترهای لوله‌باز حل می‌کنیم.

مثال اول مانومتر لوله‌باز

مانومتر لوله‌بازی حاوی جیوه با چگالی ۱۳۶۰۰ کیلوگرم بر مترمربع در تصویر زیر نشان داده شده است. مطلوب است:

1. فشار گاز داخل شیشه کروی را به‌دست آورید.
2. فشار پیمانه‌ای را محاسبه کنید.

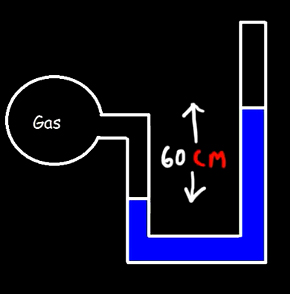
پاسخ

ابتدا قسمت یک را حل می‌کنیم. برای حل مثال‌هایی در مورد لوله‌ها یا فشارسنج‌های U شکل، ابتدا سطح مرجع را پیدا می‌کنیم. سطح مرجع برای فشارسنج نشان داده شده در تصویر بالا به صورت زیر نشان داده شده است.

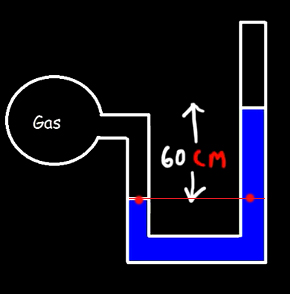
فشارهای رو به پایین در دو نقطه قرمزرنگ قرار گرفته روی خط مرجع (تصویر بالا) با یکدیگر برابر هستند:

$$P _ { \left} = P _ { \right}$$

برای آن‌که سیستم در حالت تعادل باقی بماند، نیروهای وارد شده در دو نقطه نشان داده شده نیز باید با یکدیگر برابر باشند. فشار برابر نسبت نیروی اعمال شده بر مساحت سطح است. از آنجا که مساحت دو سمت لوله U شکل با یکدیگر برابر هستند، فشار با نیرو به صورت مستقیم متناسب خواهد بود. در سمت چپ فشارسنج، فشار گاز تنها فشاری که به سمت پایین بر جیوه وارد می‌شود. لوله سمت راستِ فشارسنج، باز و در معرض فشار هوا قرار دارد.

بنابراین، در سمت راست فشارسنج، فشار اتمسفر بر جیوه وارد می‌شود. همچنین، وزن جیوه بالای خط مرجع بر نقطه قرمزرنگ نیرو وارد می‌کند:

$$ P _ { \left} = P _ {\right} P _ { gas} = P _ { atm} + \rho _ { Hg } g h$$

در این مثال، فشار جو داده نشده است. هرگاه در مثال یا مسئله‌ای مقدار فشار جو داده نشود، آن مثال یا مسئله در سطح دریا در نظر گرفته شده است. فشار جو در سطح دریا را برابر ۱۰۱۳۲۵ پاسکال در نظر می‌گیریم. با قرار دادن مقدارهای داده شده در رابطه بالا، فشار گاز را به‌دست می‌آوریم:

$$P _ { gas} = 101325 Pa + 13600 ( 9.8 ) ( 0.6 ) P _ { gas } = 181293 Pa$$

قسمت ۲: در این قسمت، فشار پیمانه‌ای را به‌دست می‌آوریم. فشار پیمانه‌ای برابر تفاضل فشار مطلق و فشار اتمسفر است:

$$P _{ gauge} = P _ {gas} - P _ { atm} P _ {gauge} = 181293 - 101325 = 79938 Pa$$

مثال دوم مانومتر لوله‌باز

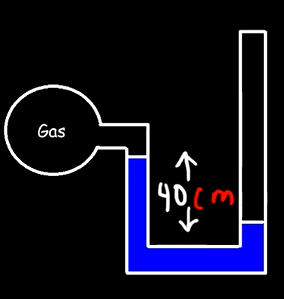
مانومتر لوله‌بازی حاوی جیوه با چگالی ۱۳۶۰۰ کیلوگرم بر مترمربع در تصویر زیر نشان داده شده است. مطلوب است:

1. فشار گاز داخل شیشه کروی را به‌دست آورید.
2. فشار پیمانه‌ای را محاسبه کنید.

پاسخ

ابتدا قسمت یک را حل می‌کنیم. این مثال نیز همانند مثال اول است، با این تفاوت که ارتفاع مایع در لوله متصل به گاز بیشتر از لوله باز است. خط مرجع به صورت زیر در تصویر نشان داده شده است.

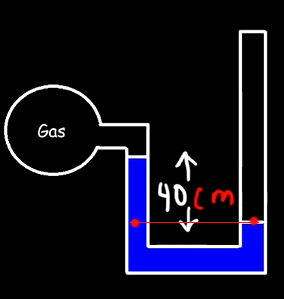
فشارهای رو به پایین در دو نقطه قرمزرنگ قرار گرفته روی خط مرجع (تصویر بالا) با یکدیگر برابر هستند:

$$P _ { \left} = P _ { \right}$$

در سمت راست فشارسنج، فشار هوا تنها فشاری که به سمت پایین بر جیوه وارد می‌شود. به این نکته توجه داشته باشید که لوله سمت راستِ فشارسنج، باز و در معرض فشار هوا قرار دارد. در سمت چپ دو فشار داریم:

• فشار گاز
• فشار حاصل از وزن جیوه بالای نقطه قرمزرنگ روی خط مرجع

$$ P _ { \left} = P _ {\right} P _ { gas} + \rho _ { Hg } g h  = P _ { atm} +$$

$$P _ {gas} = P _ {atm} - \rho _ { Hg } g h$$

$$P _ { gas} = 101325 Pa - 13600 ( 9.8 ) ( 0.4 ) P _ { gas } = 48013 Pa$$

قسمت ۲: در این قسمت، فشار پیمانه‌ای را به‌دست می‌آوریم. فشار پیمانه‌ای برابر تفاضل فشار مطلق و فشار اتمسفر است:

$$P _{ gauge} = P _ {gas} - P _ { atm} P _ {gauge} = 48013 - 101325 = - 53212 Pa$$

مثال سوم مانومتر لوله‌باز

فشارسنج U شکل نشان داده شده در تصویر زیر با مایعی با چگالی نامعلوم پر شده و اختلاف ارتفاع مایع در دو لوله برابر ۱/۳ متر است. اگر فشار گاز برابر ۹۲۰۰۰ پاسکال و لوله سمت چپ در معرض هوا قرار داشته باشد، چگالی مایع را به‌دست آورید. (فشارسنج در سطح دریا قرار دارد)

پاسخ

این مثال نیز همانند مثال‌های اول و دوم است، با این تفاوت که فشار گاز را می‌دانیم و باید چگالی مایع را به‌دست آوریم. خط مرجع به صورت زیر در تصویر نشان داده شده است.

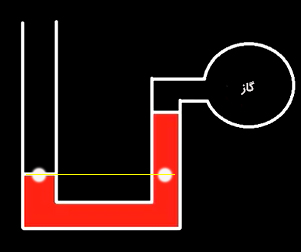
فشارهای رو به پایین در دو نقطه سفیدرنگ قرار گرفته روی خط مرجع (تصویر بالا) با یکدیگر برابر هستند:

$$P _ { \left} = P _ { \right}$$

در سمت چپ فشارسنج، فشار هوا تنها فشاری که به سمت پایین بر جیوه وارد می‌شود. به این نکته توجه داشته باشید که لوله سمت چپِ فشارسنج باز، و در معرض فشار هوا قرار دارد. در سمت راست دو فشار داریم:

• فشار گاز
• فشار حاصل از وزن جیوه بالای نقطه سفیدرنگ روی خط مرجع

$$P _ { \left} = P _ {\right} P_{atm} = P _ { gas} + \rho g h P _ { atm} - P _ { gas} = \rho g h 101325 - 92000 = \rho g h 9325 Pa = \rho (9.8 ) ( 1.3) 9325 = 12.74 \rho \rho = 732 \frac { kg } { m ^ 3 }$$

مثال چهارم مانومتر لوله‌باز

در تصویر زیر دو مانومتر باز و یک مانومتر بسته نشان داده شده‌اند. رابطه بین فشار گازهای $$x$$ و $$y$$ و $$z$$ را به دست آورید.

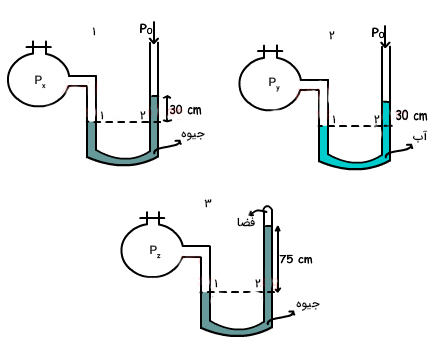
پاسخ

همان‌طور که در تصویر بالا دیده می‌شود، مانومترهای یک و سه با جیوه و مانومتر دو با آب پر شده‌اند. نخستین نکته‌ای که در حل این مثال باید به آن توجه کنیم آن است که چگالی آب کمتر از چگالی جیوه است:

$$\rho _ {water} <\; rho_ {Hg}$$

محاسبه فشار $$P _ x$$

ابتدا فشار گاز $$x$$ در مانومتر شماره یک را به‌دست می‌آوریم. خط مرجع به صورت خط‌چین در هر مانومتر نشان داده شده است. فشار در دو نقطه یک و دو با یکدیگر برابرند:

$$P_1 = P _2$$

فشار $$P_1$$ برابر فشار گاز $$x$$ و فشار $$P_2$$ برابر مجموع فشار جو و فشار حاصل از وزن جیوه قرار گرفته بالای نقطه ۲ است:

$$P _ x = P _ { atm} + \rho _ { Hg} g h P_ x  = 101325 + 13600 (9.8) (0.3) P _x = 141309 Pa$$

محاسبه فشار $$P _ y$$

در ادامه، فشار گاز $$y$$ در مانومتر شماره دو را به‌دست می‌آوریم. به این نکته توجه داشته باشید که این مانومتر به جای جیوه، با آب پر شده است. فشار در دو نقطه یک و دو با یکدیگر برابرند:

$$P_1 = P _2$$

فشار $$P_1$$ برابر فشار گاز $$x$$ و فشار $$P_2$$ برابر مجموع فشار جو و فشار حاصل از وزن آبِ قرار گرفته بالای نقطه ۲ است:

$$P _ y = P _ { atm} + \rho _ { water} g h P_ x  = 101325 + 1000 (9.8) (0.3) P _x = 104265 Pa$$

محاسبه فشار $$P _ z$$

در انتها، فشار گاز $$z$$ در مانومتر شماره سه را به‌دست می‌آوریم. توجه به این نکته مهم است که این مانومتر، مانومتری بسته و لوله سمت راست آن در معرض هوا قرار نگرفته است. مشابه دو حالت قبل، فشار در دو نقطه یک و دو با یکدیگر برابرند:

$$P_1 = P _2$$

فشار $$P_1$$ برابر فشار گاز $$x$$ و فشار $$P_2$$ برابر فشار حاصل از وزن جیوه قرار گرفته بالای نقطه ۲ است:

$$P _ z = \rho _ { Hg} g h P_ z  =  13600 (9.8) (0.75) P _x = 13607 Pa$$

با توجه به نتایج به‌دست آمده می‌بینیم فشار گاز $$x$$ بیشترین مقدار و فشار گاز $$z$$ کمترین مقدار را دارند.

مثال پنجم مانومتر لوله‌باز

اگر فشار اتمسفر برابر ۷۶۰ میلی‌متر جیوه باشد، فشار گاز درون مانومتر را در یک از حالت‌های زیر به‌دست آورید:

1. ارتفاع جیوه در لوله باز (در معرض فشار اتمسفر) به اندازه ۶۰ میلی‌متر بالاتر از ارتفاع آن در لوله متصل به گاز باشد.
2. ارتفاع جیوه در لوله متصل به گاز به اندازه ۵۰ میلی‌متر کمتر از ارتفاع آن در لوله باز (در معرض فشار اتمسفر) باشد.

پاسخ

در ابتدا قسمت یک را حل می‌کنیم. در این حالت، مانومتر به شکل نشان داده شده در تصویر زیر است. به این نکته توجه داشته باشید که در حالت یک، ارتفاع جیوه در لوله باز برابر ۶۰ میلی‌متر است.

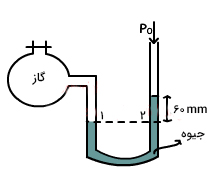
فشار گاز برابر مجموع فشار جو و فشار جیوه یا تفاضل این دو مقدار است. برای آن‌که بدانیم پاسخ قسمت یک، مجموع دو فشار یا تفاضل آن دو است باید بدانیم فشار گاز از فشار اتمسفر بیشتر است یا کمتر. برای پاسخ به این پرسش باید به ارتفاع جیوه در لوله توجه کنیم. فشار را به صورت نسبت نیرو به مساحت سطح تعریف کردیم. بنابراین، فشار اتمسفر، نیرویی به سمت پایین بر جیوه در لوله باز وارد می‌کند. به طور مشابه، گاز نیز نیرویی به سمت پایین بر جیوه اعمال می‌کند.

کدام فشار قوی‌تر است، فشار اتمسفر یا فشار گاز؟ هر دو به سمت پایین بر جیوه وارد می‌شوند. کدام فشار، جیوه را بیشتر به سمت پایین هل داده است؟ برای پاسخ به این پرسش، به سطح جیوه در هر لوله نگاه می‌کنیم. سطح جیوه در لوله متصل به گاز پایین‌تر از سطح آن در لوله باز است. بنابراین، فشار گاز، قدرت بیشتری نسبت به فشار اتمسفر دارد و جیوه را بیشتر به سمت پایین هل داده است. از این‌رو، فشار گاز باید بزرگ‌تر از فشار اتمسفر باشد. در نتیجه، فشار گاز برابر مجموع فشار اتمسفر و فشار جیوه است:

$$P _ { gas} = 760 mmHg + 60 mmHg = 820 mmHg$$

در ادامه، قسمت دوم مثال را حل می‌کنیم. در این قسمت، مانومتر به شکل نشان داده شده در تصویر زیر است. به این نکته توجه داشته باشید که در حالت دو، ارتفاع جیوه در لوله متصل به گاز برابر ۵۰ میلی‌متر یا اختلاف ارتفاع جیوه در دو لوله برابر ۵۰ میلی‌متر است.

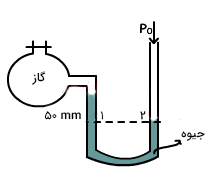
ارتفاع جیوه در لوله باز کمتر از ارتفاع آن در لوله متصل به گاز است. بنابراین، فشار اتمسفر بیشتر از فشار گاز خواهد بود. مقدار فشار اتمسفر برابر ۷۶۰ میلی‌متر جیوه است. از آنجا که فشار گاز کمتر از فشار اتمسفر است، مقدار آن برابر است با:

$$P _ { gas} = 760 mmHg - 50 mmHg = 710 mmHg$$

 تا اینجا فهمیدیم چگونه با استفاده از مانومتر، فشار گازهای مختلف را می‌توان به‌دست آورد. فشار گاز با استفاده از رابطه زیر به‌دست می‌آید:

$$P _ { gas} = P _ { atm} \pm P _ { Hg}$$

تا اینجا می‌دانیم نقش فشارسنج در تعیین مقدار فشار چیست. در ادامه، چند مثال در رابطه با لوله‌های U شکل متشکل از چند مایع غیرقابل‌امتزاج حل می‌کنیم.

 فشار در لوله های U شکل

پس از پاسخ به پرسش فشار چیست و به‌دست آوردن رابطه فشار در عمق مشخصی در شاره‌ها، چند مثال در رابطه با فشار در لوله‌های U شکل حل می‌کنیم.

مثال اول فشار در لوله U شکل

لوله U شکل نشان داده شده در تصویر زیر از آب و نفت پر شده است. اگر ارتفاع آب در این لوله برابر ۸۰ سانتی‌متر باشد، ارتفاع نفت چه مقدار است؟ (چگالی آب و نفت به ترتیب برابر ۱۰۰۰ و ۷۵۰ کیلوگرم بر مترمکعب است)

پاسخ

همان‌طور که در مطالب بالا گفته شد، فشار رو پایین در ستون چپ باید برابر فشار رو به پایین در ستون راست باشد:

$$P_ L= P _ R$$

ستون‌های راست و چپ در معرض هوا قرار دارند. بنابراین، فشار اتمسفر در هر دو سمت وجود دارد. فشار رو به پایین در ستون سمت چپ برابر مجموع فشار اتمسفر و فشار ناشی از وزن نفت و فشار در ستون راست برابر مجموع فشار اتمسفر و فشار ناشی از وزن آب است؛

$$P _ { atm } + P_ { oil} = P _ { atm} + P_ { H_2 O}$$

فشار اتمسفر از طرفین رابطه بالا حذف می‌شود.

$$P _ { oil} = P _ { H _ 2 O }$$

فشار در عمق مشخصی از شاره با استفاده از رابطه $$\rho g h$$ به‌دست می‌آید.

$$rho_1 g h_ 1 = rho_ 2 g h_ 2 rho_1 = h_ 1 = \rho _ 2 h_ 2  ( 750 ) h_ 1 = 1000 (\times (0.8 ) h_ 1 = 1.07 m$$

مثال دوم فشار در لوله U شکل

لوله U شکلی از آب با چگالی ۱۰۰۰ کیلوگرم بر مترمکعب در ستون سمت راست و نفت در ستون سمت چپ پر شده است. چگالی نفت چه مقدار است؟

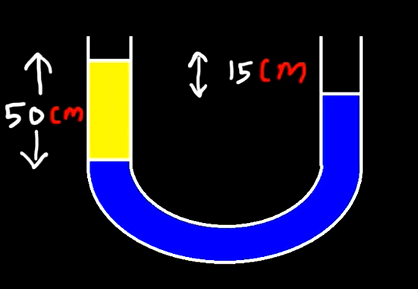
پاسخ

ابتدا خط مرجع را رسم می‌کنیم.

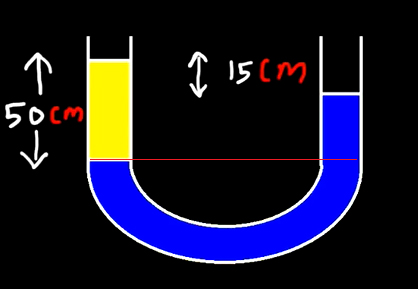
ارتفاع آب بالای خط مرجع برابر $$h = 50 cm - 15 cm = 35 cm$$ است.

$$P _ { oil} = P _ {H_ 2 O} rho_{oil}g h_ { oil} = \rho _ {H2 O} g h_ {H_2 O} rho_{oil} ( 0.5) = 1000 \times 0.35 rho_{oil} = 700 \frac { kg} { m ^ 3}$$

مثال سوم فشار در لوله U شکل

بالابر هیدرولیک چیست ؟

فشار نقش مهمی در زندگی روزمره ایفا می‌کند. یکی از مهم‌ترین کاربردهای فشار در صنعت، استفاده از آن در بالابرهای هیدرولیک است. در بالابرهای هیدرولیک از سیستم استوانه‌ای هیدرولیک برای بالا بردن، حرکت و جابجایی اجسام سنگین استفاده می‌شود. گرچه طراحی‌های بالابرهای هیدرولیک با توجه به کاربرد آن‌ها متغیر است، اجزای مشابهی در ساخت آن‌ها استفاده می‌شود. بالابرهای هیدرولیکی در فیزیک به شکل آسانسوری هستند که توسط فشار مایعی مناسب کار می‌کنند. هیدرولیک بالابر ساده‌ای در تصویر زیر نشان داده شده است.

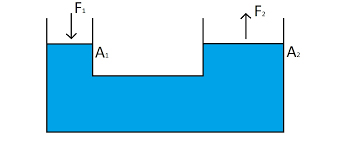
اگر نیرویی به بزرگی $$F_1$$ بر پیستون سمت چپ به مساحت $$A_1$$ وارد شود، نیرویی برابر $$F_2$$ بر پیستون سمت راست به مساحت $$A_2$$ وارد می‌شود به گونه‌ای که:

$$\frac { F_ 1} { A_ 1} = \frac { F_ 2 } { A_ 2}$$

اثبات: هنگامی که نیروی $$F_1$$ بر پیستون سمت چپ در تصویر نشان داده شده در بالا وارد می‌شود، فشار ناشی از این نیرو برابر است با:

$$\triangle P = \frac { F_ 1} { A_ 1}$$

این فشار از طریق مایع درون هیدرولیک به پیستون سمت راست منتقل می‌شود:

$$\triangle P = \frac { F_ 2} { A_ 2}$$

در نتیجه، رابطه $$\frac { F_ 1} { A_ 1} = \frac { F_ 2 } { A_ 2}$$ اثبات می‌شود.

مثال اول بالابر هیدرولیک

نیرویی برابر $$F_ 1 = 100 N$$ بر پیستون سمت چپِ هیدرولیک بالابر به مساحت ۰/۰۲ مترمربع وارد می‌شود. اگر مساحت پیستون سمت راست برابر ۰/۰۸ مترمربع باشد،‌ مقدار نیروی $$F_ 2$$ رابه‌دست آورید.

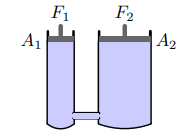
پاسخ

از آنجا که فشار وارد شود توسط نیروی $$F_ 1$$ در پیستون سمت چپ، از طریق مایع درون هیدرولیک به پیستون دیگر منتقل می‌شود، داریم:

$$\frac { F_ 1} { A_ 1} = \frac { F_ 2 } { A_ 2}$$

با قرار دادن مقدارهای داده شده در مثال، مقدار نیروی $$F_ 2$$ را به‌دست می‌آوریم:

$$F_ 2 = \frac { F _ 1 A_2 } { A_ 1 } F_ 2 = \frac { 100 \times 0.08 } { 0.0} = 100 \times 4 = 400 N$$

مثال دوم بالابر هیدرولیک

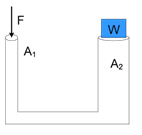
هیدرولیک بالابری به شکل نشان داده شده در تصویر زیر داریم. مساحت پیستون باریک برابر ۵ سانتی‌متر مربع و مساحت پیستون پهن برابر ۵۰ سانتی‌متر مربع است. اگر وزن جسم W برابر ۱۸۰۰ نیوتن باشد، بزرگی نیروی F برای بالا بردن جسم W چه مقدار خواهد بود؟

پاسخ

از آنجا که فشار وارد شود توسط نیروی $$F_ 1$$ در پیستون سمت چپ، از طریق مایع درون هیدرولیک به پیستون دیگر منتقل می‌شود، داریم:

$$\frac { F_ 1} { A_ 1} = \frac { F_ 2 } { A_ 2}$$

با قرار دادن مقدارهای داده شده در مثال، مقدار نیروی $$F_ 2$$ را به‌دست می‌آوریم:

$$F_ 2 = \frac { F _ 1 A_2 } { A_ 1 } F_ 2 = \frac { 1800 \times 5 } { 50} = 180  N$$

مثال سوم بالابر هیدرولیک

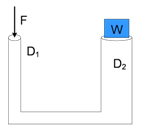
بالابر هیدرولیکی با پیستون‌هایی به قطرهای $$D_ 1$$ و $$D_2$$ در تصویر زیر نشان داده شده است. اگر $$D_ 1 = 5 cm$$ و $$D_ 1 = 15 cm$$ و وزن جسم $$W$$ برابر ۱۸۰۰ نیوتن باشد، کمینه نیروی F برای بالا بردن این جسم چه مقدار است؟

پاسخ

همان‌طور که در مطالب بالا اشاره شد فشار ایجاد شده توسط نیروی $$F_ 1$$ در پیستون سمت چپ، از طریق مایع درون هیدرولیک به پیستون دیگر منتقل می‌شود، داریم:

$$\frac { F_ 1} { A_ 1} = \frac { F_ 2 } { A_ 2}$$

در این مثال، قطر هر یک از ستون‌های استوانه‌ای داده شده است. از آنجا که  سطح مقطع استوانه‌ها به شکل دایره است، مساحت آن‌ها برابر $$\pi r ^2$$ خواهد بود. با قرار دادن رابطه مساحت در فرمول بالا داریم:

$$\frac { F _ 1 } {\pi ( \frac { D_ 1} { 2 } ) ^ 2 = \frac { F _ 2 } {\pi ( \frac { D_ 2} { 2 } ) ^ 2 } \frac { F_ 1} { D _ 1 ^ 2 } = \frac { F_ 2 } { D_ 2^ 2} }$$

با قرار دادن مقدارهای داده شده در رابطه بالا داریم:

$$\frac { F _ 1 } { 5 ^ 2 } = \frac { 1800} {15 ^ 2 } F = 1800 \times ( \frac { 5 } { 15 } ) ^ 2 = \frac { 1800 } { 9} = 200$$

توجه به این نکته مهم است که قطرهای داده شده به متر تبدیل نشدند، زیرا $$10 ^ { -2}$$ از طرفین ساده می‌شدند.

مثال چهارم بالابر هیدرولیک

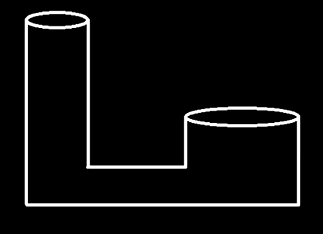
بالابر هیدرولیکی در تصویر زیر نشان داده شده است. نیرویی برابر ۱۰۰ نیوتن و به سمت پایین بر پیستون کوچک این بالابر به قطر ۵۰ سانتی‌متر وارد می‌شود.

1. نیروی رو به بالای وارد شده از طرف پیستون بزرگ‌تر به قطر ۲ متر را به‌دست آورید.
2. بازده مکانیکی این بالابر هیدرولیکی چه مقدار است؟
3. اگر نیروی ۱۰۰ نیوتنی، پیستون کوچک‌تر را به اندازه ۲ متر به سمت پایین حرکت دهد، پیستون بزرگ‌تر تا چه ارتفاعی بالا خواهد رفت؟

پاسخ

از آنجا که فشار وارد شود توسط نیروی $$F_ 1$$ در پیستون سمت چپ، از طریق مایع درون هیدرولیک به پیستون دیگر منتقل می‌شود، داریم:

$$\frac { F_ 1} { A_ 1} = \frac { F_ 2 } { A_ 2}$$

نیروی $$F_1$$ نیروی وارد شده بر پیستون کوچک‌تر و به سمت پایین (نیروی ورودی) و نیروی $$F_2$$ نیروی وارد شده بر پیستون بزرگ‌تر و به سمت بالا (نیروی خروجی) است. رابطه بالا را برحسب $$F_ 2$$ مرتب می‌کنیم:

$$F_ 2 = F_ 1 \times \frac { A_2 } {A _ 1}$$

اگر نیروی رو به پایینی بر پیستون کوچک‌تر وارد کنیم، نیروی رو بالای بزرگ‌تری بر پیستون بزرگ‌تر وارد می‌شود. بنابراین، هرچه سطح مقطع پیستونی بزرگ‌تر باشد، نیروی وارد شده بر آن نیز بزرگ‌تر خواهد بود. در ابتدا قسمت یک را پاسخ می‌دهیم.

قسمت ۱: مساحت برابر $$\pi r ^ 2$$ است. در این مثال، قطر پیستون‌ها داده شده است، بنابراین برای به‌دست آوردن مساحت هر پیستون باید قطر داده شده را بر دو تقسیم کنیم:

$$F_ 2 = 100 \times \frac {\pi (1) ^ 2  } {\pi ( 0.25^ 2} F _ 1 = 1600 N$$

قسمت ۲: در این قسمت بازده مکانیکی بالابر را به‌دست می‌آوریم. بازده مکانیکی به صورت نسبت نیروی خارجی به نیروی وارد شده تعریف می‌شود. نیروی خارجی، نیروی وارد شده از طرف بالابر و نیروی داخلی، نیروی وارد شده بر بالابر است:

$$Mechanical advantage = \frac { F_ { out}} { F_ { \in} }$$

$$MA = \frac { 1600 N} { 100 n} = 16$$

قسمت ۳: نیروی وارد شده بر پیستون کوچک‌تر آن را به اندازه ۲ متر به سمت پایین جابجا می‌کند. در این قسمت می‌خواهیم بدانیم پیستون بزرگ‌تر تا چه ارتفاعی به سمت بالا حرکت می‌کند. دو راه برای حل این قسمت وجود دارد.

راه حل اول

توجه به این نکته مهم است که حجم مایع داخل بالابر هیدرولیک در سراسر آن یکسان است. از این‌رو، تغییر حجم مایع در پیستون کوچک‌تر باید برابر تغییر حجم آن در پیستون بزرگ‌تر باشد. دلیل این موضوع آن است که حجم مایع ثابت است و نمی‌تواند تغییر کند.

$$V_ 1 = V _ 2$$

حجم از حاصل‌ضرب ارتفاع در مساحت به‌دست می‌آید.

$$A_ 1 h _ 1 = A_2 h _2 \pi r _ 1 ^ 2 h _ 1 = \pi r_ 2 ^ 2 h_ 2 (0.25) ^ 2 \times 2 = ( 1 ) ^ 2 \times h_2 h_ 2 = 0.125 m$$

راه حل دوم

کار انجام شده توسط نیروی کوچک‌تر برابر کار انجام شده توسط نیروی بزرگ‌تر است:

$$W_ 1 = W_ 2$$

دلیل این تساوی به پایستگی انرژی مربوط می‌شود.

$$F_ 1 h _ 1 = F_ 2 h  _ 2$$

مقدارهای نیروها و جابجایی پیستون کوچک‌تر را در رابطه بالا قرار می‌دهیم و جابجایی پیستون بزرگ‌تر را به‌دست می‌آوریم:

$$100 ( 2 ) = 1600 ( h _ 2 ) h _ 2 = 0.125 m$$

مثال پنجم بالابر هیدرولیک

اتومبیلی به جرم ۱۵۰۰ کیلوگرم روی پیستون بزرگ‌تر بالابر هیدرولیکی به شعاع ۴ متر قرار گرفته است.

1. کمینه نیروی لازم برای بالا بردن اتومبیل چه مقدار است؟
2. اگر بازده مکانیکی این بالابر برابر ۲۰ باشد، کمینه نیروی وارد شده به سمت پایین برای بالا بردن اتومبیل چه مقدار است؟
3. شعاع پیستون کوچک‌تر را به‌دست آورید.
4. فشار وارد شده از طرف پیستون بزرگ‌تر چه مقدار است؟
5. برای بالا بردن ماشین به اندازه ۲ متر، پیستون کوچک‌تر باید تا چه ارتفاعی به سمت پایین حرکت کند؟

پاسخ

قسمت ۱: نیروی جاذبه زمین، نیرویی به سمت پایین و برابر mg بر ماشین وارد می‌کند. در مقابل، پیستون نیز نیرویی برابر $$F _ 2$$ به سمت بالا بر ماشین وارد می‌کند. بنابراین، مقدار کمینه نیروی وارد شده از طرق پیستون برای بالا بردن ماشین  با سرعت ثابت، برابر mg است. اگر مقدار $$F_ 2$$ از mg بیشتر شود، ماشین با شتاب شروع به حرکت به سمت بالا خواهد کرد. برای آن‌که ماشین را با سرعت ثابت به سمت بالا حرکت دهیم، نیروی $$F_2$$ باید برابر mg باشد.

$$F_ 2 = mg = 1500 ( 9.8) = 147000 N$$

قسمت ۲: در این قسمت با داشتن بازده مکانیکی بالابر هیدرولیکی باید مقدار کمینه نیروی به سمت بالا از طرف پیستون بزرگ‌تر را به‌دست آوریم. همان‌طور که در مطالب بالا گفتیم، نیروی کوچک‌تر بر پیستون کوچک‌تر و نیروی بزرگ‌تر بر پیستون بزرگ‌تر وارد می‌شود. از آنجا که بازده مکانیکی برابر ۲۰ است، نیروی کوچک‌تر یعنی $$F_ 1$$ باید $$\frac { 1 } { 20 }$$ نیروی $$F_2$$ باشد. از این‌رو، مقدار نیروی $$F_1$$ برابر است با:

$$F_ 1 = \frac { F_ 2 } { 20} = \frac { 147000} { 20 } F_ 1 = 735 N$$

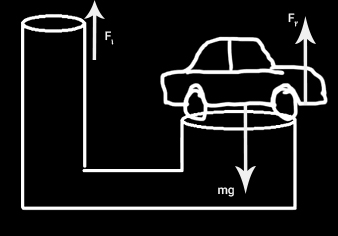
قسمت ۳: بر طبق اصل پاسکال، فشار وارد شده بر هر پیستون باید با یکدیگر برابر باشند:

$$P _ 1 = P _ 2$$

از آنجا که فشار برابر نیرو بر مساحت است، رابطه بالا را به صورت زیر می‌نویسیم:

$$\frac { F_ 1 } { A_ 1 } = \frac { F_ 2 } { A_ 2}$$

معادله بالا را کمی مرتب‌تر می‌نویسیم:

$$F_1 A_2 = F_2 A_1$$

طرفین رابطه بالا را هم‌زمان بر $$F_1$$ و $$A_ 1$$ تقسیم می‌کنیم:

$$\frac { F_ 1 A_ 2 } {F_ 1 A_ 1 } = \frac { F_ 2 A_ 1 } { F_ 1 A_ 1 }$$

در سمت راست رابطه، $$A_ 1$$ و در سمت چپ رابطه $$F_ 1$$ ساده می‌شوند:

$$\frac { F_ 2 } { F_ 1 } = \frac { A_ 2 } { A_ 1}$$

بر طبق رابطه بالا، نسبت نیروها برابر نسبت مساحت‌ها با یکدیگر است. بازده مکانیکی به صورت نسبت نیروی خروجی به نیروی ورودی تعریف می‌شود.

$$MA = \frac { F_ 2 } { F_ 1}$$

با توجه به رابطه بالا، بازده مکانیکی را می‌توان به صورت زیر نیز نوشت:

$$MA = \frac { A_ 2 } { A_ 1 }$$

از آنجا که سطح مقطع پیستون‌ها به شکل دایره است، مساحت آن‌ها برابر $$\pi r ^ 2$$ است:

$$MA = \frac {\pi r _ 2 ^ 2 } { \pi r _ 1 ^ 2 }$$

بازده مکانیکی برابر ۲۰ و شعاع پیستون بزرگ‌تر برابر ۴ متر است:

$$20 = \frac  { 4 ^ 2 } { r _ 1 ^ 2 } 16 = 20 r _1^ 2 r_ 1 = 0.89 m$$

بنابراین، با دانستن بازده مکانیکی و شعاع یکی از پیستون‌ها، شعاع پیستون دیگر را می‌توانیم به راحتی به‌دست آوریم.

قسمت ۴: در این قسمت، فشار وارد شده از طرف پیستون بزرگ‌تر را به‌دست می‌آوریم.

$$P_ 2 = \frac { F_ 2 } { A_ 2 } P_2 = \frac {147000 N} { \pi (4)^ 2  } P_2 = 292. 4 Pa$$

قسمت ۵: در این قسمت فرض شده است که ماشین به کمک بالابر هیدرولیکی به اندازه ۲ متر به سمت بالا جابجا می‌شود. برای انجام این کار باید بدانیم، پیستون کوچک‌تر چه اندازه به سمت پایین حرکت می‌کند. راحت‌ترین راه برای حل این قسمت، استفاده از پایستگی انرژی است. بنابراین، کار انجام شده توسط پیستون کوچک‌تر برابر کار انجام شده توسط پیستون بزرگ‌تر است:

$$W_ 1 = W_ 2$$

کار، برابر حاصل‌ضرب نیرو در جابجایی است:

$$$$F_ 1 d_ 1 = F_2 d_2 735 N d_1 = 147000 times ( 2 ) d_1  = frac { 147000 times 2 } { 735}  d_1 = 40 m

نکته: به هنگام حل مسائل مربوط به بالابر هیدرولیکی به فرمول‌های زیر نیاز داریم:

• بازده مکانیکی برابر نسبت نیروی خروجی به نیروی ورودی است:

$$MA = \frac {F_ 2 } { F_ 1 } = \frac { A_ 2 } { A_ 1 } = \frac {d_1} { d_2}$$

• اگر مساحت پیستون را افزایش دهیم، نیروی خروجی نیز افزایش می‌یابد. اما مقدار جابجایی پیستونِ بزرگ‌تر کاهش خواهد یافت.
• نیروی خارجی را می‌توانیم با استفاده از رابطه زیر به‌دست آوریم:

$$F_ 2 = F_ 1 \times \frac { A_2 } { A_ 1 }$$

• کار انجام شده توسط پیستون کوچک‌تر برابر کار انجام شده توسط پیستون بزرگ‌تر است:

  $$W_ 1 = W_ 2$$

• فشار و حجم در بالابر هیدرولیک ثابت هستند:

$$V_ 1 = V_ 1 P _ 1 = P _ 2$$

تا اینجا می‌دانیم فشار چیست و در شاره‌ها چگونه به‌دست می‌آید. همچنین، در مطالب بالا فهمیدیم انواع فشار چیست. در ادامه، در مورد نوع دیگری از فشار به نام فشار جزیی به صورت خلاصه صحبت می‌کنیم.

فشار جزیی چیست ؟

در مطالب بالا فهمیدیم فشار چیست و با استفاده از چه روابطی به‌دست می‌آید. همچنین، با تعریف فشارهای مطلق و پیمانه‌ای آشنا شدیم. در این بخش در مورد فشار جزیی صحبت می‌کنیم. محفظه‌ای را در نظر بگیرید که با چند گاز مختلف پر شده است. هر گاز بر دیواره‌های محفظه فشار وارد می‌کند. به فشار وارد شده از طرف هر گاز در مخلوطی از گازهای مختلف، فشار جزیی گفته می‌شود. در زندگی روزمره، به هنگام استفاده از فشارسنج برای بررسی فشار اتمسفر در بیرون، فشار گاز را اندازه می‌گیریم. با انجام این کار، مشخصه فیزیکی ماکروسکوپی تعداد زیادی از مولکول‌های گاز را اندازه گرفته‌ایم. در مقیاس مولکولی، فشار به دلیل نیروی وارد شده بر دیواره ظرف پس از برخورد مولکول‌های گاز به آن، ایجاد می‌شود.

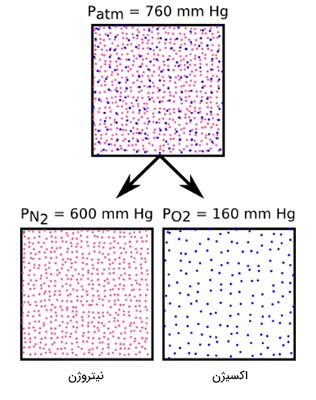
اکنون می‌دانیم انواع فشار چیست. فشار جزیی یکی از انواع فشار است که برای محاسبه مقدار آن از نظریه گاز کامل استفاده می‌شود.

گاز ایده ال و فشار جزیی

در این بخش، گازهای مختلف در مخلوط گازی داخل محفظه را به صورت گاز ایده‌ال در نظر می‌گیریم. این فرضیه تا هنگامی صحیح است که دمای گاز خیلی پایین نباشد و فشار در محدوده یک اتمسفر باشد. این بدان معنا است دو فرضیه مهم را در مورد مولکول‌های گاز در نظر گرفته‌ایم:

• مولکول‌های گاز هیچ حجمی را اشغال نکرده‌اند.
• هیچ جاذبه بین‌مولکولی بین مولکول‌های گاز وجود ندارد. این بدان معنا است که مولکول‌های گاز مستقل از یکدیگر فعالیت می‌کنند.

با استفاده از این فرضیه‌ها می‌توانیم سهم گازهای مختلف در مخلوط را در فشار کلی به‌دست آوریم. به فشار اعمال شده توسط هر گاز در مخلوط، فشار جزیی می‌گوییم. فشار جزیی را می‌توانیم با استفاده از قانون گاز ایده‌ال محاسبه کنیم.

مثال محاسبه فشار جزیی

فرض کنیم مخلوطی از گاز هیدروژن،‌ $$H_ 2 ( g )$$ و گاز اکسیژن، $$O _ 2 ( g )$$ داریم. این مخلوط از ۶/۷ مول گاز هیدروژن و ۳/۳ مول گاز اکسیژن تشکیل شده است. مخلوط گازها در محفظه‌ای به حجم ۳۰۰ لیتر و در دمای ۲۷۳ کلوین قرار دارد. اگر فشار کل مخلوط گازی برابر ۰/۷۵ اتمسفر باشد، فشار جزیی گاز هیدروژن را به‌دست آورید.

پاسخ

سهم گاز هیدروژن در فشار کل همان فشار جزیی این گاز است. از آنجا که مولکول‌های گاز ایده‌ال مستقل از گازهای دیگر در مخلوط رفتار می‌کنند، فشار جزیی گاز هیدروژن برابر مقدار فشار در حالتی است که هیچ گاز دیگری در محفظه وجود ندارد. در نتیجه، برای به‌دست آوردن فشار جزیی این گاز می‌توانیم به طور کامل گاز هیدروژن را نادیده بگیریم و از قانون گاز ایده‌ال به صورت زیر استفاده کنیم:

$$P _ { H _ 2} V = n_ {H _ 2 } RT$$

رابطه بالا را برحسب $$P _ { H _ 2 }$$ مرتب می‌کنیم:

$$P _{ H_ 2 } = \frac {n_ { H _ 2 } RT}  { V}$$

با قرار دادن مقدارهای داده شده در مثال، فشار جزیی گاز هیدروژن را به‌دست می‌آوریم:

$$P _{ H_ 2 } = \frac {(6.7 mol )  ( 0.08206 \frac { atm. L } { mol . K  } ) ( 273 K)}  { 300 L} = 0.50 atm$$

جمع‌بندی

در این مطلب، موارد زیر را به طور کامل با مثال بررسی کردیم.

• آموختیم فشار چیست و با استفاده از رابطه کلی $$P = \frac { F } { A}$$ به‌دست می‌آید.
• فهمیدیم یکای فشار چیست. پاسکال و میلی‌متر جیوه دو واحد اصلی اندازه‌گیری فشار هستند.
• فشار در شاره‌ها را به‌دست آوردیم و در مورد اصل پاسکال صحبت کردیم.
• فشار در عمق مشخصی از شاره را به‌دست آوردیم. فشار در عمق مشخصی از شاره با استفاده از رابطه $$$$rho g h به‌دست می‌آید.
• چگونگی اندازه‌گیری فشار گاز در فشارسنج را با حل مثال‌های مختلف توضیح دادیم.
• فهمیدیم انواع فشار چیست و با فشارهای جزیی، مطلق و پیمانه‌ای آشنا شدیم.
• با بالابرهای هیدرولیک با حل چند مثال آشنا شدیم.