فشار پیمانه ای چیست؟ – به زبان ساده با مثال و تمرین


فشار انواع مختلفی دارد، مانند فشار جو، فشار مطلق و فشار خلاء. یکی از مهمترین انواع فشار، «فشار پیمانه ای» (Gauge Pressure) یا فشار گیج است که به آن «فشار نسبی» هم گفته میشود. اگر فشار جو را از کل فشاری که به یک ماده وارد میشود، کم کنیم، فشار پیمانه ای بهدست میآید. در این مطلب از مجله فرادرس ابتدا توضیح میدهیم که فشار پیمانه ای چیست. سپس با توضیح انواع فشار، معرفی فرمولهای هر کدام و حل مثالهای مختلف، به شما کمک میکنیم تا نحوه تشخیص و محاسبه فشار پیمانه ای را در موقعیتها و مسائل مختلف بیاموزید.
فشار پیمانه ای چیست؟
اگر فشار کل (فشار مطلق) وارد بر یک جسم برابر با P باشد و فشار جو (فشار اتمسفر یا فشار هوا) را P0 در نظر بگیریم، در این صورت فشار پیمانه ای Pg (فشار گیج) برابر است با اختلاف بین فشار جو و فشار مطلق که با فرمول نشان داده میشود. از طرفی با توجه به اینکه فشار در شارهها برابر است با ، بنابراین فشار پیمانه ای در شارهها از رابطه زیر بهدست میآید:
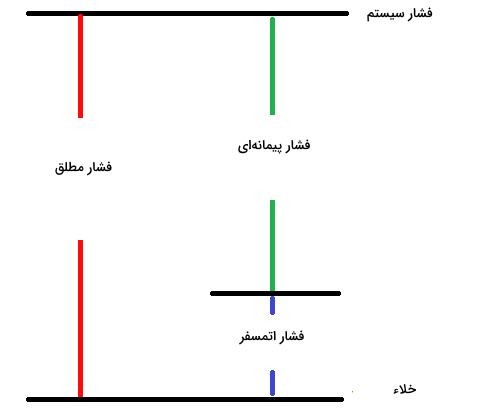
نمودار بالا ارتباط بین سه نوع فشار شامل فشار مطلق، فشار جو و فشار پیمانه ای را بهخوبی نشان میدهد. مشخص است که از مجموع مقادیر فشار پیمانه ای و فشار جو، فشار مطلق یا فشار کل سیستم حاصل میشود. بنابراین اگر بخواهیم فشار پیمانه ای یک سیستم را پیدا کنیم، لازم است فشار جو را از فشار کل سیستم کم کنیم.
واحد فشار پیمانه ای
در این قسمت میخواهیم ببینیم واحدهای فشار پیمانه ای چیست. بسته به نوع کاربرد و ترجیح ما، فشار پیمانه ای توسط واحدهای مختلفی میتواند بیان شود. دو مورد از مرسومترین واحدهای بکار رفته برای این نوع فشار عبارتاند از:
- پاسکال (Pa)
- پوند بر اینچ مربع (psi)
واحد استاندارد یا SI برای بیان فشار پیمانه ای، پاسکال است و در متون آموزشی و حل مسائل، معمولا فشار پیمانه ای بر حسب این واحد نوشته میشود. یک پاسکال برابر است با یک نیوتن (N) بر متر مربع (m2):
از این واحد فشار پیمانه ای بیشتر در صنعت استفاده میشود. یک psi فشاری است که توسط نیرویی برابر با یک پوند (Ib) بر سطحی با مساحت یک اینچ مربع (in2) وارد میشود:
تبدیل psi به Pa با استفاده از رابطه بالا انجام میشود. واحدهای دیگری مانند میلیمتر جیوه (mmHg)، اینچ ستون آب (inH2O) و بار (bar) نیز برای فشار پیمانه ای بکار میروند. در برخی متون برای اینکه نشان دهند فشار اندازهگیری شده فشار پیمانه ای است، حرف g را در انتهای واحد مینویسند (برای مثال psig).

واحدهای بالا برای بیان فشار مطلق هم بکار میروند، اما واحدی به نام اتمسفر (atm) معمولا فقط برای بیان فشار مطلق و فشار اتمسفر استفاده میشود. همچنین در واحدی به شکل psia، حرف a در انتهای psi بیانگر این است که عدد اعلام شده مربوط به مقدار فشار مطلق است. در بخشهای بعد، پس از مطالعه فرمول کلی فشار، متوجه خواهید شد که چگونه پاسکال و psi تعریف شدهاند.
یادگیری فشار پیمانه ای با فرادرس
تا اینجا متوجه شدیم فشار پیمانه ای چیست. پیش از اینکه به بررسی تفاوتهای این نوع فشار با فشار مطلق بپردازیم، اگر دانشآموز هستید، میدانید که مبحث «فشار و آثار آن» در درس سوم از کتاب علوم نهم آموزش داده میشود و در کتاب درسی فیزیک دهم نیز، با توضیح مبحث «فشار در شارهها» به فشار پیمانه ای اشاره شده است. با مشاهده فیلمهای آموزشی مربوط به این کتابهای درسی، میتوانید یادگیری بهتری را با فرادرس در این زمینه کسب کنید:

- فیلم آموزش علوم نهم بخش فیزیک فرادرس
- فیلم آموزش فیزیک دهم فرادرس
- فیلم آموزش فیزیک دهم مرور و حل تمرین فرادرس
تفاوت فشار پیمانه ای و فشار مطلق
پس از اینکه یاد گرفتیم تعریف و فرمول فشار پیمانه ای چیست، مهم است که تفاوت آن را با فشار مطلق بدانیم. اگر دقت کنید در تصویر زیر برای هر کدام از سه نوع فشار مطلق، پیمانه ای و اتمسفر، یک مبدا یا نقطه صفر وجود دارد. نقطه صفر تعریف فشار اتمسفر و فشار مطلق، فشار خلاء است، در حالی که مبدا تعریف فشار پیمانه ای، فشار اتمسفر یا فشار جو است. طبق این تصویر، بهطور کلی دو مبدا برای تعریف فشار داریم: اتمسفر و خلاء.
- فشار کل یا فشار مطلق: فشاری است که نسبت به خلاء کامل سنجیده میشود. منظورمان از خلاء کامل، نبود مطلق هیچ نوع فشاری است، یعنی داریم P=۰.
- فشار پیمانه ای یا فشار نسبی یا فشار گیج: فشاری است که نسبت به اتمسفر سنجیده میشود.
در جدول زیر تفاوتهای این دو نوع فشار بیان شده است:
| انواع فشار | فشار پیمانه ای (Pg) | فشار مطلق (P) |
| فرمول | ||
| مبدا اندازهگیری | فشار اتمسفر | خلاء (فشار مطلق صفر) |
| کاربردها | سیستمهای پنوماتیک و هیدرولیک، مخازن تحت فشار | سیستمهای خلاء، ترمودینامیک |
| وسایل اندازهگیری | مانومتر | بارومتر |
فشارسنج و فشار پیمانه ای
حالا ممکن است سوالات مهمی مطرح شوند، اینکه فشارسنجها کدام نوع فشار را اندازه میگیرند؟ فشار پیمانه ای یا فشار مطلق؟ وسیله اندازهگیری فشار پیمانه ای چیست؟ فشاری که در فشارسنجها اندازهگیری میشود، فشار پیمانه ای است. برای اینکه بتوانیم به این سوالات پاسخ دهیم، لازم است دو نکته را در مورد فشار اتمسفر بدانیم. اولین نکته این است که اثر فشار جو در تمام اندازهگیریهای ما همیشه وجود دارد، به جز در شرایط خاص، مثل اینکه سیستم در خلاء کامل باشد.
نکته بعدی این است که مقدار فشار اتمسفر تقریبا ثابت است، . بنابراین اگر فشارسنج فشار مطلق را اندازهگیری کند، همیشه بخشی از عدد به دست آمده مربوط به فشار اتمسفر است و اگر بخواهیم فشار واقعی سیستم را بدانیم، نیاز است را از عدد اعلام شده توسط فشارسنج، کم کنیم. اما اگر فشارسنج فشار پیمانه ای را اندازهگیری کند، عدد اعلام شده شامل عدد فشار جو نیست. پس مطمئن هستیم که این عدد با فشار سیستم موردنظرمان کاملا برابر است.

به عبارت دیگر، این روش اندازهگیری به ما اجازه میدهد روی فشار واقعی اعمال شده توسط سیستم یا فرآیند مدنظرمان تمرکز کنیم، بدون اینکه درگیر آثار فشار محیط باشیم. پس در مرجع فشار پیمانه ای، مقدار فشار اتمسفریک یا فشار هوا در محاسبات وارد نمیشود. در عوض، فشار پیمانه ای از فشار هوا بهعنوان نقطه صفر خود استفاده میکند. یکی از ملموسترین اندازهگیریهای فشار پیمانه ای، اندازهگیری فشار خون است.
فرمول فشار
برای اینکه بهتر یاد بگیریم فشار پیمانه ای چیست، لازم است ابتدا با مفهوم فشار و انواع آن بیشتر آشنا شویم تا بتوانیم از فرمول فشار پیمانه ای بهدرستی استفاده کنیم. اما پیش از آن پیشنهاد میکنیم اگر دانشجو هستید و به دنبال حل تمرین بیشتر در زمینه «فشار و شارهها»، از فیلم آموزشی فیزیک ۳ – حل تمرین فرادرس که لینک آن در ادامه برای شما قرار داده شده است، استفاده کنید:
فشار یک کمیت فیزیکی نردهای یا عددی محسوب میشود و برابر است با مقدار نیروی عمودی وارد بر سطح یک ماده. طبق این تعریف، فرمول کلی فشار به شکل زیر است:
در رابطه بالا اندازه نیروی F بر حسب نیوتن (N) و سطح مقطع A بر حسب متر مربع (m2) است. بنابراین واحد فشار، نیوتن بر متر مربع یا پاسکال است که با Pa نشان داده میشود. انواع مختلف فشار ممکن است با واحدهای مختلفی بیان شوند، اما واحد استاندارد برای تمام انواع فشار در سیستم بینالمللی واحدها یا SI، پاسکال است.
از تعریف و فرمول بالا برای فشار مشخص است که دو عامل خیلی مهم در فشار وارد شده به یک جسم موثراند:
- مقدار نیرویی که بهصورت عمودی به سطح یک جسم وارد میشود.
- مساحت سطحی که نیرو به آن وارد میشود یا نیرو روی آن توزیع میشود.
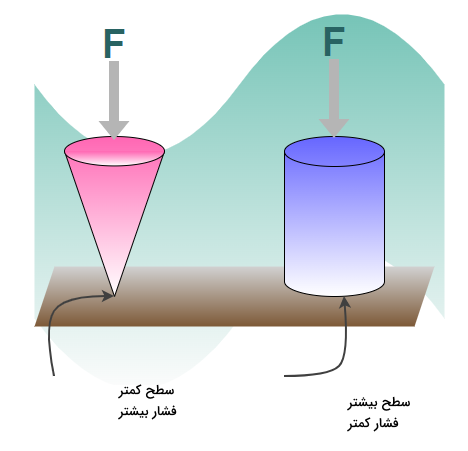
در مورد اول، هر چه مقدار نیرویی عمودی وارد بر سطح یک جسم بیشتر باشد، فشار وارد بر آن هم بیشتر است. یعنی بین نیروی F و فشار P رابطه مستقیم وجود دارد:
در مورد دوم، هر چه سطح مقطعی که نیرو به آن اعمال میشود، کوچکتر باشد، فشار بیشتری خواهیم داشت. پس بین A و P رابطه معکوسی برقرار است:
در انتهای این بخش، پیشنهاد میکنیم چنانچه دانشآموز پایه دهم هستید، مطلب «فرمول های فیزیک دهم در یک نگاه» از مجله فرادرس را مطالعه کنید. در این نوشته، خلاصهای از فرمولهای فیزیک دهم که شامل فرمولهای مبحث فشار پیمانه ای نیز میشود، گردآوری شده است.
فرمول فشار پیمانه ای در شارهها
در این بخش لازم است مبحث فشار در شارهها مطرح شود تا ببینیم در شارهها فرمول فشار پیمانه ای چیست. گفتیم فرمول کلی فشار پیمانه ای بهصورت زیر است:
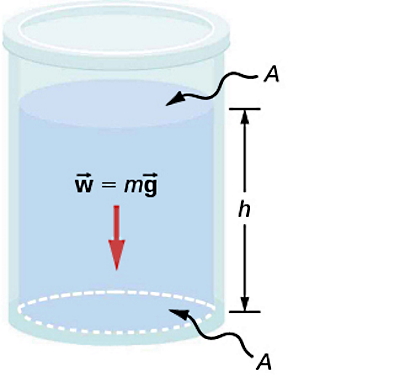
فرض کنید شارهای به شکل بالا در حالت تعادل و بدون هیچ گونه حرکتی است، یعنی دنبال فشار استاتیک هستیم. منظورمان از شاره یا سیال، انواع مایعات و گازها است، اما در این بخش شاره را یک مایع در نظر میگیریم. میخواهیم ببینیم فشاری که این شاره با چگالی ρ به ته ظرفی با ارتفاع h و سطح مقطع A وارد میکند، چقدر است و فرمول آن را به دست آوریم. از فرمول کلی فشار شروع میکنیم:
ابتدا باید ببینیم نیرویی که در اینجا به سطح پایینی یا کف ظرف وارد میشود، چیست. این نیرو، نیروی وزن مایع یا شارهای است که روی این سطح قرار گرفته است. بنابراین . با قرار دادن این نیرو در رابطه بالا داریم:
از طرفی میتوانیم جرم شاره را بر حسب چگالی آن بازنویسی کنیم. میدانیم فرمول چگالی برابر است با . بنابراین :
هنوز هم امکان سادهسازی بیشتر رابطه بالا هست. اگر حجم ظرف استوانهای شکل را بخواهیم حساب کنیم، باید از فرمول حجم استوانه استفاده کنیم:
پس فشاری که این شاره به کف ظرف وارد میکند، برابر است با:
طبق فرمول این فشار فقط و فقط به چگالی شاره، عمق آن و مقدار شتاب جاذبه زمین بستگی دارد. پس فشار ناشی از یک شاره در حالت سکون، ناشی از نیروی وزن آن است. حالا میخواهیم ببینیم این فشار از چه نوعی است، یعنی آیا فشار پیمانه ای محسوب میشود یا فشار مطلق است؟ اگر بخواهیم دقیقتر بررسی کنیم، فشار هوا نیز میتواند روی فشار کلی که بر کف ظرف وارد میشود، اثر گذار باشد.

بنابراین برای محاسبه فشار کل وارد بر کف ظرف (P) که ناشی از نیروی وزن مایع (Pg) و فشار هوای روی سطح مایع است (P0)، باید بنویسیم:
این فشار همان فشار مطلق است که در مورد آن صحبت کردهایم. بنابراین فشار ناشی از وزن شاره، همان فشار پیمانه ای است و میتوانیم برای محاسبه فشار پیمانه ای در شارهها فرمول زیر را بنویسیم:
دقت کنید فشار در گازها بهعنوان نوع دیگری از شارهها، به عواملی مثل دما نیز وابسته است. در نتیجه مبحث پیچیدهتری ایجاد میکند که در این مطلب نمیگنجد. نکته مهمی که در مورد فشار در مایعات وجود دارد این است که همواره فشار برای دو نقطه از یک مایع که در عمق برابری قرار دارند، یکسان است.
حل مثال و تمرین از فشار پیمانه ای
پس از اینکه کاملا یاد گرفتیم مفهوم فشار پیمانه ای چیست و تفاوت آن را با سایر انواع فشار فرا گرفتیم، در این بخش با حل مثالها و تمرینهای متنوع به شما کمک میکنیم تا به نحوه استفاده از فرمولهای این مبحث مسلط شوید.
مثال ۱
فشار پیمانه ای ناشی از آب جمع شده پشت سدی با ارتفاع ۱۰ m، چقدر است؟ (شتاب g برابر است با و چگالی آب است)
پاسخ
برای محاسبه فشار پیمانه ای ناشی از یک شاره، از فرمولی که در انتهای بخش قبل گفتیم، استفاده میکنیم:
مثال ۲
اگر یک محفظه مربع شکل با ۵۰۰ L آب کاملا پر شده باشد، فشار پیمانه ای و فشار کل وارد بر کف این محفظه چند پاسکال است؟ (شتاب g برابر است با و چگالی آب است)
پاسخ
برای محاسبه فشار پیمانه ای باید از فرمول زیر استفاده کنیم:
اما مقدار h را نداریم و لازم است به اطلاعات صورت سوال مراجعه کنیم. در سوال حجم آب داخل محفظه داده شده است. محفظه یک مکعب است و تمام آن با آب کاملا پر شده است. پس اگر آب داخل محفظه را مکعبی با ضلع a در نظر بگیریم و از فرمول حجم مکعب استفاده کنیم، خواهیم داشت:
دقت کنید با محاسبه یک ضلع مکعب، در واقع h را پیدا کردهایم. در سوال حجم بر حسب لیتر داده شده است. ولی برای داشتن فشار بر حسب پاسکال لازم است طول h را به متر داشته باشیم. یعنی باید لیتر به متر مکعب تبدیل شود. میدانیم هر متر مکعب برابر است با هزار لیتر:
اگر دو طرف رابطه بالا را در ۱۰-۳ ضرب کنیم، خواهیم داشت:
مجددا دو طرف رابطه بالا در عدد ۵۰۰ ضرب میکنیم:
پس حجم آب بر حسب متر مکعب بهدست آمد. حالا میتوانیم عمق آب را محاسبه کنیم:
با داشتن h، حالا میتوانیم فشار پیمانه ای را پیدا کنیم:
همچنین مقدار فشار کل یا فشار مطلق هم خواسته شده است. پس باید فشار اتمسفر را با این مقدار جمع کنیم:

مثال ۳
در مورد یه منبع گازی با دانستن اینکه فشار اتمسفریک ۱۴ psi و فشار پیمانه ای اندازهگیری شده ۳۹ psi است، فشار کل را برای این فشار پیمانه ای خوانده شده محاسبه کنید:
پاسخ
فشار کل همان فشار مطلق است که از مجموع فشار پیمانه ای و فشار هوا بهدست میآید:
چون در سوال ذکر نشده است که فشار کل بر حسب چه واحدی محاسبه شود، بنابراین نیازی به تغییر واحد نیست.
مثال ۴
در عمق ۱۱ m از سطح دریا، فشار پیمانه ای و فشار مطلق آب به ترتیب چقدر هستند اگر فشار اتمسفر را ۱۰۲٫۲۱۳ kN.m2 در نظر بگیریم (شتاب g برابر است با و چگالی آب است):
پاسخ
فشار پیمانه ای برای آب دریا در یک عمق مشخص، از رابطهای که برای فشار پیمانه ای در شارهها نوشتیم، حاصل میشود:
با قرار دادن مقادیر عددی خواهیم داشت:
دقت کنید واحد پاسکال برابر بود با نیوتن بر متر مربع یا N/m2. بنابراین فشار اتمسفر با مقدار ۱۰۲٫۲۱۳ kN.m2 در واقع دارای همین واحد است، فقط به کیلو تبدیل شده است. پس برای اینکه راحتتر کار کنیم، میتوانیم فشار پیمانه ای محاسبه شده را بر حسب کیلو پاسکال بنویسیم تا بهراحتی با فشار اتمسفر جمع شده و فشار مطلق حاصل شود:
حالا میرویم سراغ حساب کردن فشار مطلق با فرمول زیر:
مثال ۵
اگر هر کدام از ظرفهای زیر تا ارتفاع ۱۰ cm با آب پر شده باشند، در کدام یک مقدار فشار پیمانه ای در کف ظرف بیشتر است؟
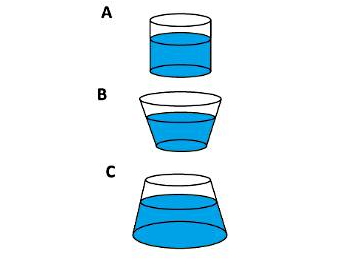
پاسخ
فشار پیمانه ای ناشی از یک مایع برابر است با فشار ناشی از ستون مایع. در اینجا فشار در کف هر ظرف خواسته شده است. طبق فرمول ، مقدار فشار پیمانه ای در کف هر ظرف فقط و فقط به چگالی مایع یعنی چگالی آب و ارتفاع یا عمق مایع در ظرف وابسته است. با توجه به اینکه چگالی و عمق برای هر سه طرف برابر است، پس مقدار فشار پیمانه ای در کف هر سه ظرف یکسان است.
تمرین ۱
عبارت ریاضیاتی درست برای فشار پیمانه ای چیست، اگر ستونی از مایع با چگالی ρ و ارتفاع h در معرض فشار هوا با مقدار ۱۰۵ قرار داشته باشد؟
گزینه آخر درست است. همانطور که گفتیم فشار پیمانه ای یا فشار گیج برای ستونی از مایع برابر است با فشار در مایعات که با فرمول محاسبه میشود.
تمرین ۲
فشار خون فشار مطلق محسوب میشود.
درست
غلط
گزینه دوم درست است. فشار خون نوعی فشار پیمانه ای است.
تمرین ۳
فرض کنید دو تانک آب داریم که هر دو تا ارتفاع یکسانی پر شدهاند. اگر سطح مقطع تانک اول دو برابر سطح مقطع تانک دوم باشد، ارتباط بین مقادیر فشار پیمانه ای در کف دو تانک چگونه است؟
فشار پیمانه ای در کف هر دو تانک با هم برابر است.
فشار پیمانه ای در کف تانک اول نصف فشار در کف تانک دوم است.
فشار پیمانه ای در کف تانک اول دو برابر فشار در کف تانک دوم است.
هیچکدام
گزینه اول درست است. اگر به فرمول فشار پیمانه ای در مایعات توجه کنید، فشار پیمانه ای فقط به عمق مایع و چگالی آن بستگی دارد. در این سوال چگالی مایع و ارتفاع آن برای هر دو تانک یکی است. پس فشار پیمانه ای برای هر دو برابر است.
تمرین ۴
اگر فشار مطلق خوانده شده برای یک ابزار ۳۸٫۸ psi و فشار هوا ۱۵ psi باشد، فشار پیمانه ای کدام گزینه است؟
گزینه دوم درست است. برای محاسبه فشار پیمانه ای، کافی است فشار اتمسفر را از فشار کل کم کنیم:
تمرین ۵
فشار پیمانه ای در عمق ۹۹۰ m از یک اقیانوس چند اتمسفر است، اگر چگالی آب اقیانوس ۱٫۰۲×۱۰۳ kg/m۳ باشد (شتاب g برابر است با )؟
فشار پیمانه ای در لولههای U شکل (مانومتر)
در این بخش میآموزیم که روش اندازهگیری فشار پیمانه ای چیست. گفتیم که مقدار فشار برای تمام نقاطی از یک مایع که در یک عمق قرار دارند، مقدار یکسانی است. از این نتیجهگیری در ساخت وسیلهای به نام «مانومتر» (Manometer) استفاده میشود. مانومتر وسیلهای است که برای اندازهگیری فشار پیمانه ای بکار میرود و کاربرد دیگر آن، محاسبه چگالی مایعات مختلف است.
نحوه اندازهگیری فشار در مانومتر بر اساس این نکته است که اگر فشار در یک سمت لوله U شکل بیشتر از سمت دیگر باشد، این اختلاف فشار برابر است با فشار پیمانه ای که از اندازهگیری اختلاف ارتفاع ستون مایع در دو طرف لوله بهدست میآید. کافی است اختلاف ارتفاع اندازهگیری شود (h) و طبق فرمول زیر، در چگالی مایع و شتاب جاذبه ضرب شود تا فشار پیمانه ای محاسبه بهدست آید:
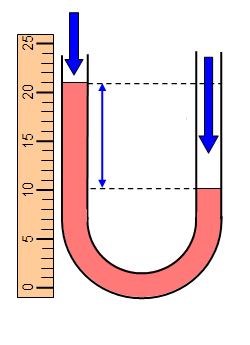
برای نمونه فرض کنید میخواهید از مانومتری به شکل بالا برای اندازهگیری فشار پیمانه ای ریههای خود استفاده کنید. کافی است در یک طرف لوله بدمید (سمت راست لوله در تصویر بالا) و تغییرات ارتفاع مایع را در سمت دیگر با یک خطکش اندازه بگیرید. اگر مایع داخل مانومتر آب باشد، شتاب گرانش زمین ۱۰ m/s2 در نظر گرفته شود و اختلاف ارتفاعی به اندازه ۱۱ cm ایجاد شده باشد، در این صورت مقدار فشار پیمانه ای در ریههای شما برابر است با:
دقت کنید در محاسبه بالا برای اینکه فشار بر حسب پاسکال بهدست آید، حتما باید اختلاف ارتفاع از سانتیمتر به متر تبدیل شود. در ادامه این بخش، با بررسی سه حالت مختلف مفهوم فشار پیمانه ای در لولههای U شکل یا مانومتر را کاملا متوجه خواهید شد.
نکته: منظورمان از فشار پیمانه ای همان فشاری است که بالاتر از فشار اتمسفریک است.
نکته: معمولا در مسائل کلمه پیمانه ای بکار نمیرود، اما در واقع فشاری که از شما خواسته میشود، همان فشار پیمانه ای است.
حالت اول
شکل زیر یک لوله U شکل یا مانومتری را نشان میدهد که از یک نوع مایع با چگالی ρ تا نیمه پر شده است. دو طرف این لوله باز است و هر دو طرف در معرض فشار هوا قرار دارند. انتظار داریم فشار در دو نقطه با عمق برابر مثل نقاط A و B برابر باشد، یعنی .
همچنین با توجه به اینکه مایع از دو طرف بهصورت یکسان در معرض هوا قرار دارد، باید ارتفاع ستون مایعی که بالای نقطه B قرار دارد با ارتفاع ستون مایعی که بالای نقطه A قرار دارد، برابر باشد، یعنی داشته باشیم . در ادامه میخواهیم درستی این رابطه را نشان دهیم.
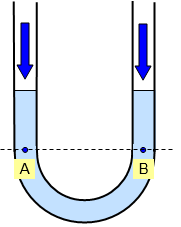
فشار کل در نقطه A برابر است با مجموع فشار ستون مایع بالای نقطه A و فشار هوا. در نقطه B نیز فشار کل برابر است با مجموع فشار ستون مایع بالای این نقطه و فشار هوا. تمام توضیحاتی که دادیم، در روابط زیر خلاصه میشوند:
با حذف فشار هوا از دو طرف تساوی، خواهیم داشت:
چون مایع در دو طرف یکسان است، پس چگالی ρ و شتاب جاذبه g نیز از دو طرف ساده میشوند. بنابراین ثابت میشود که اگر هر دو دهانه لوله U شکل پر شده از یک نوع مایع، بهصورت یکسان درمعرض هوا قرار بگیرند، ارتفاع ستون مایع در دو طرف لوله برابر است.
حالت دوم
میخواهیم ببینیم در دومین حالتی که برای لولههای U شکل در نظر گرفتهایم، وضعیت فشار پیمانه ای چیست. در این حالت، فرض کنید در دهانه سمت راست لوله هوا دمیده شده است (P1). باز هم انتظار داریم فشار در دو نقطه A و B برابر باشد، چون در هر دو نقطه عمق مایع از سطح متناظر با کف لوله یکسان است. میخواهیم نشان دهیم در این موقعیت ارتفاع ستون مایعی که بالای نقطه B قرار میگیرد، نسبت به ارتفاع ستون مایعی که بالای نقطه A قرار گرفته است، کمتر خواهد شد، یعنی داریم . سپس فرمول فشار پیمانه ای را برای این موقعیت مینویسیم.
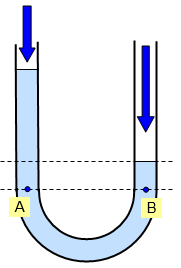
ابتدا فشار کل در نقطه A را بررسی میکنیم که برابر است با مجموع فشار ستون مایع بالای نقطه A و فشار هوا. ولی در این حالت فشار کل در نقطه B با فشار کل در نقطه B در حالت اول متفاوت است و برابر میشود با مجموع فشار ستون مایع بالای این نقطه، فشار هوا یا P0 و فشاری که در این بخش از لوله دمیده شده است (P1). پس میتوانیم روابط زیر را بنویسیم:
با حذف فشار هوا از دو طرف تساوی، به رابطه زیر میرسیم:
به تفاوت این رابطه با رابطه مشابه در حالت اول دقت کنید. در اینجا یک جمله اضافی داریم به نام P1. پس امکان ندارد که ارتفاع ستون دو مایع در دو طرف لوله یعنی hA و hB با هم برابر باشند. اما میتوانیم یک نتیجهگیری دیگر داشته باشیم. اگر دو طرف این رابطه را بر ρg تقسیم کنیم، خواهیم داشت:
با توجه به اینکه مقدار چگالی مایع، شتاب جاذبه زمین و P1 همگی مثبت هستند، پس جمله بهعنوان یک عدد مثبت با ارتفاع hB جمع میشود تا با hA برابر شود. پس همیشه hB از hA کوچکتر است:
پس در این حالت محاسبه فشار پیمانه ای با فرمول زیر امکانپذیر است:
حالت سوم
در آخرین حالتی که بررسی میکنیم، فرض شده است که لوله U شکل مانومتر از دو نوع مایع مختلف پر شده است. پس در این حالت دو چگالی مختلف بهصورت ρA و ρB داریم. همچنین فرض کنید که مقدار چگالی مایع زرد رنگ یعنی ρB از چگالی مایع آبی یعنی ρA بیشتر است. انتظار داریم در چنین شرایطی باز هم مانند حالت دوم، ارتفاع ستون مایع در سمت راست لوله یعنی hB از ارتفاع ستون مایع در سمت راست یعنی hA کمتر شود. در ادامه این مسئله را ثابت میکنیم.
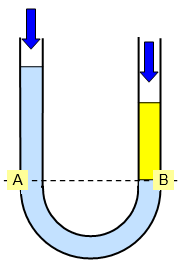
دقت کنید با اینکه در این حالت ستون مایع بالای نقاط A و B از دو مایع متفاوت تشکیل شده است، اما باز هم فشار در نقاط A و B باید برابر باشد. علت این است که فشار این نقاط بر اساس عمقی از مایع که زیر این نقاط قرار میگیرد، محاسبه میشود. زیر هر دو نقطه A و B، یک نوع مایع داریم. فشار کل در نقطه A برابر است با مجموع فشار ستون مایع بالای نقطه A و فشار هوا. همچنین فشار کل در نقطه B نیز میشود مجموع فشار ستون مایع بالای این نقطه و فشار هوا. پس خواهیم داشت:
در نوشتن روابط بالا باید دقت کنیم که چون دو نوع مایع مختلف داریم، پس مقادیر چگالی متفاوت هستند و قابلیت ساده شدن چگالیها مانند حالتهای قبل وجود ندارد.
با ساده کردن P0 از دو طرف، به عبارت زیر میرسیم:
میتوانیم g را هم از دو طرف خط بزنیم:
این عبارت بیشتر از این امکان سادهسازی ندارد. اما با توجه به اینکه میدانیم ، پس برای برقراری تساوی بالا لازم است داشته باشیم:
نکته: فرمول در شرایطی که چگالی یک مایع مشخص است، برای محاسبه چگالی مایع دوم بکار میرود.
حل مثال و تمرین از فشار پیمانه ای در لولههای U شکل
پس از اینکه یاد گرفتید انواع حالتهای ممکن در مانومتر برای فشار پیمانه ای چیست و نحوه محاسبه آن در لولههای U شکل چگونه است، در این بخش چند مثال عددی و تمرین برای شما در نظر گرفتهایم تا به این مبحث نیز کاملا مسلط شوید.
مثال ۱
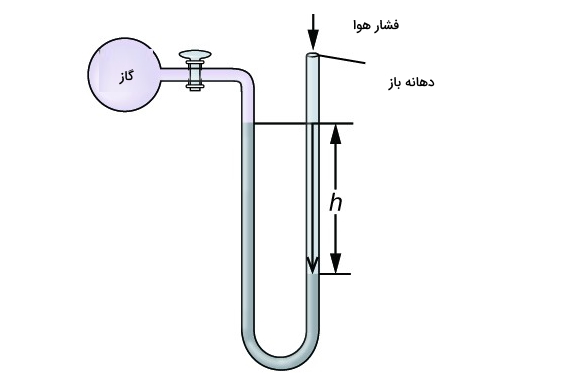
یک مانومتر جیوهای برای اندازهگیری فشار گاز داخل یک فلاسک بکار میرود. فرض کنید سطح جیوه در بازوی متصل به فلاسک بالاتر باشد و اختلاف سطح جیوه در دو طرف مانومتر ۴۳ mm اندازهگیری شود. فشار گاز را بر حسب الف) میلیمتر جیوه، ب) کیلو پاسکال و ج) اتمسفر حساب کنید (فشار بارومتریک = ۷۳۷ mmHg):
پاسخ
برای اینکه موقعیت مانومتر را تجسم کنید، بهتر است شکل آن را رسم کنید. با در نظر گرفتن فشار گاز داخل محفظه بهصورت P و فشار هوا بهصورت P0، طبق شکل زیر مجموع فشار گاز و فشار ستون جیوه از سمت راست و فشار هوا از سمت چپ به سطح جیوه داخل مانومتر وارد میشوند.
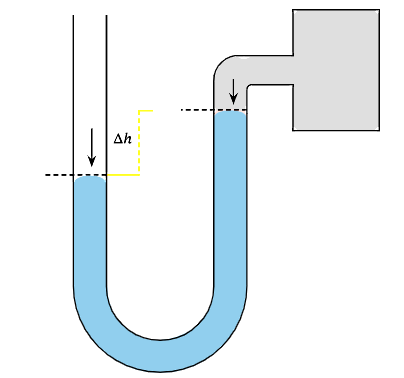
حالا دو نقطه هم سطح مثل A و B در نظر میگیریم، طوری که نقطه A در بازوی سمت چپ شکل و کاملا روی سطح جیوه قرار داشته باشد. نقطه B را نیز در بازوی راست مانومتر و کاملا همسطح با نقطه A در نظر میگیریم. میدانیم که مقدار فشار برای دو نقطه A و B با عمق برابر، مساوی است. پس داریم:
فشار گاز داخل محفظه از رابطه بالا بهدست میآید. حالا دقت کنید در قسمت الف مقدار فشار بر حسب mmHg خواسته شده است. چون در این سوال شاره موردنظر ما جیوه است، پس برای داشتن فشار پیمانه ای بر حسب میلیمتر جیوه کافی است عمق شاره را به میلیمتر بنویسیم. یعنی فشار پیمانه ای ستون جیوه در معادله بالا برابر است با ۴۳ mmHg:
همچنین مقدار فشار بارومتریک که همان فشار هوا است، به میلیمتر جیوه داده شده است. پس محاسبه فشار گاز با واحد میلیمتر جیوه خیلی سر راست است:
حالا میرویم سراغ قسمت ب در سوال. برای پاسخ دادن به این قسمت نیاز داریم تبدیل واحد میلیمتر جیوه به پاسکال را بدانیم. در بخشهای بعدی با توضیح بارومتر متوجه خواهید شد که . با استفاده از این رابطه فشار داخل محفظه گازی را به پاسکال تبدیل میکنیم:
فراموش نکنید که فشار بر حسب کیلو پاسکال خواسته شده بود. در نهایت قسمت ج را جواب میدهیم که فشار بر حسب واحد اتمسفر یا atm خواسته شده است. با توجه به تبدیل واحد زیر و با استفاده از جواب قسمت ب، خواهیم داشت:
مثال ۲
شکل زیر یک لوله U شکل را نشان میدهد که از آب و مایع P پر شده است. فرض کنید مایع P قابلیت حل شدن در آب را ندارد. با توجه به اینکه چگالی آب ۱۰۰۰ kg/m3 است، چگالی مایع P چقدر است؟
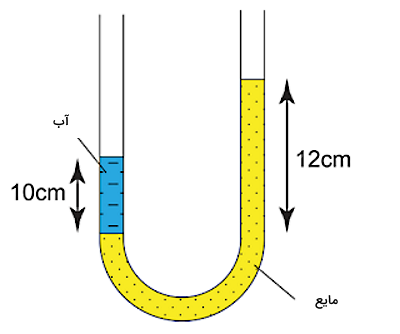
پاسخ
شرایط در شکل بالا مشابه حالت سوم از بخش قبل است. برای اینکه بتوانیم چگالی مایع P را بهدست آوریم، کافی است مقدار فشار را در دو نقطه هم ارتفاع A و B که بهصورت زیر در نظر گرفته میشوند، بنویسیم:
- نقطه A را ابتدای ستون آبی رنگ آب در نظر میگیریم.
- نقطه B هم دقیقا در همین ارتفاع ولی در سمت دیگر لوله و در مایع P قرار دارد.
- فشار مایع P در این دو نقطه یکسان است، چون هر دو نقطه روی عمق برابری از ماده P قرار گرفتهاند. پس داریم: .
حالا در رابطه بالا عددگذاری میکنیم. فراموش نشود که مقادیر ارتفاع بر حسب سانتیمتر هستند که میتوانند به متر تبدیل شوند. در این نوع مثالها چون نسبتها مهم هستند، تغییر واحد الزامی نیست:
مثال ۳
در شکل زیر برای هر کدام از دو حالت، فشار پیمانه ای کدام یک از مقادیر Pgas ،PL و Patm محسوب میشود و چه ارتباطی با دو فشار دیگر دارد؟
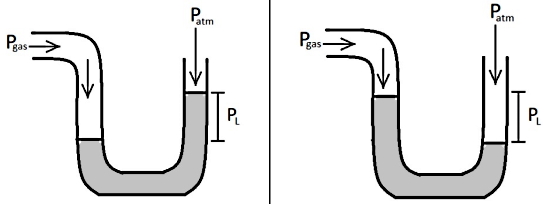
پاسخ
- ابتدا به بررسی تصویر سمت راست میپردازیم:
در این تصویر اگر دو نقطه با عمق برابر در مایع در نظر بگیریم، طوری که یک نقطه در بازوی راست لوله U و دقیقا روی سطح مایع باشد (A) و نقطه دیگر همسطح با آن و در بازوی چپ لوله (B)، در این صورت فشار این دو نقطه برابر است. یعنی داریم:
در بازوی راست این لوله، تنها فشاری که به نقطه A وارد میشود، فشار هوا یا Patm است:
در بازوی سمت چپ لوله، فشار وارد بر نقطه B برابر است با مجموع فشار ستون مایع بالای این نقطه یا PL که همان فشار پیمانه ای است و فشار گاز یا Pgas:
حالا از برابری این دو فشار خواهیم داشت:
پس رابطه فشار پیمانه ای با دو فشار دیگر برای تصویر سمت راست به این صورت شد.
- حالا تصویر سمت چپ در شکل سوال را بررسی میکنیم:
باز هم دو نقطه با عمق برابر مثل A و B داخل مایع در نظر میگیریم، به این صورت که نقطه A در بازوی راست لوله کاملا همسطح با نقطه B در بازوی چپ قرار میگیرد. نقطه B را کاملا روی سطح مایع انتخاب میکنیم. حالا از مساوی بودن فشار این دو نقطه استفاده میکنیم:
فشار در نقطه A در بازوی راست برابر است با مجموع فشار ستون مایع یا همان فشار پیمانه ای PL و فشار اتمسفر یا Patm:
این در حالی است که فشار در نقطه B در بازوی چپ لوله بفقط ناشی از فشار گاز یا Pgas است:
با مساوی قرار دادن این دو فشار و سادهسازی، فشار پیمانه ای به شکل زیر بهدست خواهد آمد:
پس فشار پیمانه ای در هر دو حالت برابر است با فشار ستون مایع یا PL.
مثال ۴
طبق شکل زیر، فشار یک مخزن گازی در سطح دریا توسط یک مانومتر جیوهای با یک بازوی بسته اندازهگیری میشود. فشار گاز چند پاسکال است؟
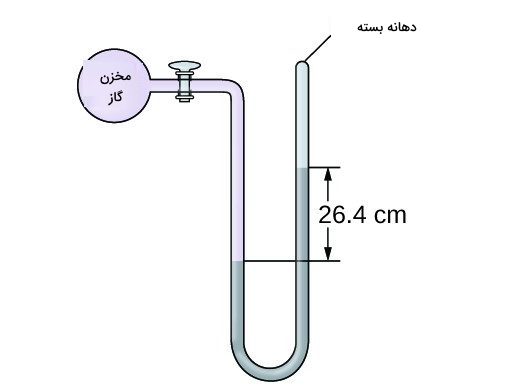
پاسخ
ابتدا نقاط هم عمق در داخل مایع جیوه را تعیین میکنیم. نقطه A در بازوی راست لوله در ابتدای ارتفاع ۲۶٫۴ cm انتخاب میشود و نقطه B کاملا همسطح با این نقطه در بازوی چپ روی سطح مایع. فشار در این دو نقطه برابر است:
فشاری که به A وارد میشود ناشی از ستون مایعی است که بالای این نقطه قرار دارد (فشار پیمانه ای). چون دهانه لوله در این قسمت بسته است، پس هوا وارد این بخش نشده است و خلاء داریم. بنابراین فشار در بخش بالای لوله صفر است:
فشار وارد بر نقطه B ناشی از فشار گاز داخل محفظه است:
پس فشار گاز در این مانومتر با فشار پیمانه ای برابر است. حالا برای محاسبه فشار پیمانه ای بهجای ضرب کردن مقادیر چگالی و جاذبه و ارتفاع h، چون مایع داخل مانومتر جیوه است، میتوانیم از راه سادهتری استفاده کنیم. با تبدیل ارتفاع بر حسب میلیمتر، فشار گاز که همان فشار پیمانه ای است، میشود ۲۶۴ mmHg:
در سوال فشار بر حسب پاسکال خواسته شده است. با توجه به اینکه میدانیم ، پس فشار گاز بر حسب گاز میشود:
مثال ۵
مانومتر جیوهای زیر به یک مخزن آب متصل است. به توجه به اطلاعات داده شده، فشار نقطه C که در ابتدای مخزن آب و سر بازوی چپ قرار دارد، چند پاسکال است (g=۹٫۸ m/s۲)؟
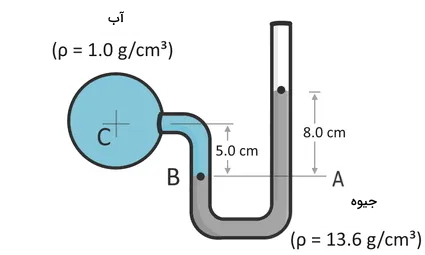
پاسخ
در این مانومتر دو نوع مایع داریم، پس احتمالا از فرمول فشار در مایعات باید دو بار استفاده کنیم. برای حل این سوال هم دو نقطه A و B را مطابق شکل بالا، همسطح هم و در یک نوع مایع، طوری که در ابتدای یک ارتفاع داده شده قرار بگیرد، در نظر میگیریم. دقت کنید که چون هر دو نقطه در یک مایع یعنی جیوه قرار دارند، پس میتوانیم از اصل برابری فشار در این دو نقطه استفاده کنیم. اما اگر نقطه A کمی بالاتر انتخاب شود، دیگر فشار برابری با نقطه B نخواهد داشت:
فشار نقطه A برابر است با فشار ستون جیوه روی آن. همچنین با توجه به بسته بودن انتهای بازوی راست، قسمت بالای این لوله خلاء است و فشار آن صفر است:
دقت کنید حتما باید مقادیر چگالی و ارتفاع اندیس جیوه (Hg) یا آب (w) داشته باشند تا در محاسبات اشتباه نکنید. از طرفی فشار نقطه B برابر است با مجموع فشار ستون آبی که روی آن قرار دارد و ارتفاع آن مشخص است به اضافه فشار مخزن آب که همان PC در نظر میگیریم:
حالا کافی است که عددگذاری کنیم. اما قبل از آن، چون فشار به پاسکال خواسته شده است، باید چگالیها بر حسب واحد استاندارد kg/m۳ نوشته شوند. میدانیم پیشوند سانتی در کنار هر واحدی به معنای ۱۰-۲ است:
در آخرین مرحله از این نکته استفاده کردیم که هر کیلوگرم برابر است با ۱۰۰۰ گرم:
تمرین ۱
در شکل زیر کدام گزینه در مورد فشار پیمانهای صحیح است؟
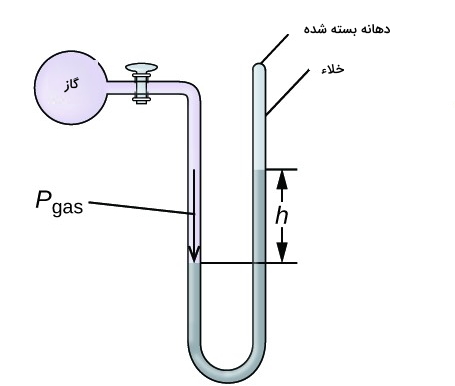
تمرین ۲
در شکل زیر کدام گزینه در مورد فشار پیمانهای صحیح است؟
تمرین ۳
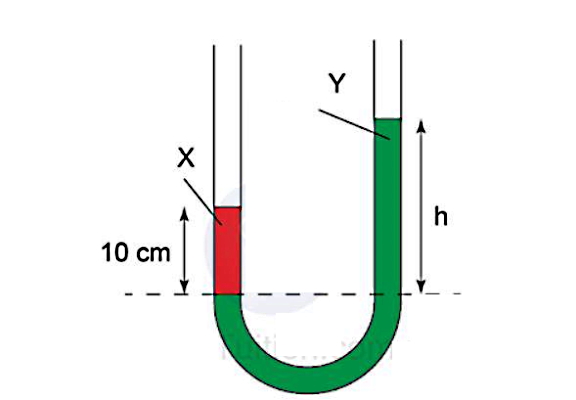
شکل زیر لوله U شکلی را نشان میدهد که از دو نوع مایع با نامهای X و Y پر شده است. اگر چگالی دو مایع X و Y بهترتیب برابر باشد با ۱۲۰۰ kg/m۳ و ۸۰۰ kg/m۳، مقدار h در شکل کدام گزینه است؟
فشار پیمانه ای منفی
تا اینجا آموختیم که مرجع فشار پیمانه ای چیست. منظورمان از مرجع فشار پیمانه ای این است که در اندازهگیریها یا محاسبات خود به دنبال یافتن مقدار فشار پیمانه ای هستیم، نه فشار مطلق. انتخاب درست مرجع مناسب برای فشار، در اندازهگیریهای دقیق صنعتی خیلی مهم است و نیازمند داشتن اطلاعاتی است که در این بخش توضیح میدهیم.
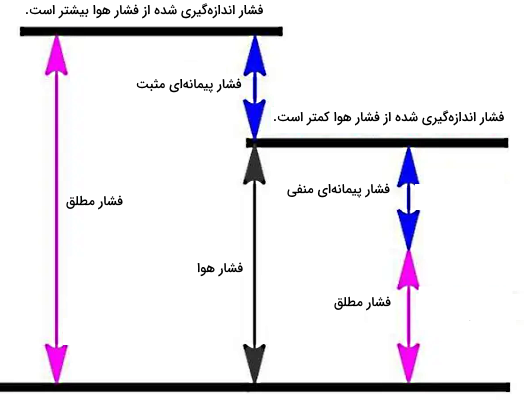
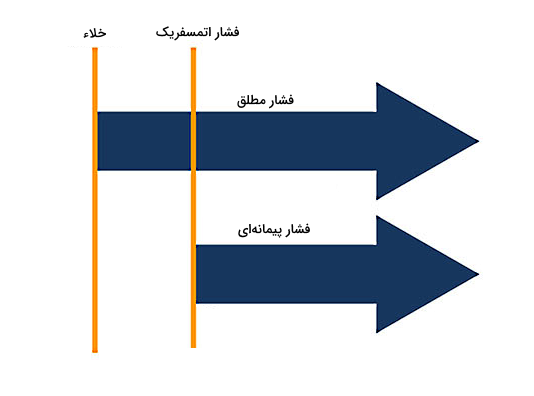
اگر خاطرتان باشد در ابتدای مطلب، به تفاوت فشار پیمانه ای و فشار مطلق و مبدا این دو نوع فشار اشاره کردیم. در عمل، فشار پیمانه ای میتواند مثبت یا منفی باشد. به شکل بالا دقت کنید:
- فشار پیمانه ای مثبت (سمت چپ تصویر) نشاندهنده این است که فشار اندازهگیری شده از فشار اتمسفر بیشتر است.
- فشار پیمانه ای منفی (سمت راست تصویر) که به آن فشار خلاء هم گفته میشود، علامت این است که فشار اندازهگیری شده از فشار اتمسفر کمتر است.
پس طبق نمودار در شرایطی که فشار پیمانه ای منفی است، فشار اتمسفر یا فشار جو برابر است با مجموع فشار پیمانه ای منفی و فشار مطلق:
در اکثر آزمایشهای فیزیک نیازمند شرایط ویژهای هستیم و لازم است آزمایش در یک محفظه خلاء انجام شود. یک محفظه خلاء طوری طراحی میشود که هوای آن به سمت خارج پمپ شود. بنابراین فشار هوا در داخل چنین محیطی از فشار هوای بیرون کمتر است و فشارسنج این محفظه، فشار گیج منفی گزارش میکند.

بنابراین مهم است که با توجه به علامت فشار پیمانه ای بتوانیم تشحیص دهیم فشار کل چه وضعیتی دارد. بخصوص اینکه در برخی موارد نیاز است حتما فشار مطلق را بدانیم. برای مثال در سیستم یخچال، فشار گیج برای اندازهگیری فشار در خطوط سردکننده مهم است. این در حالی است که برای تحلیل عملکرد پمپهای خلاء و کمپرسور، اطلاع از فشار مطلق اهمیت دارد.
فشار اتمسفر چیست؟
در ادامه یادگیری خود راجع به این موضوع که فشار پیمانه ای چیست، در این قسمت به توضیح فشار اتمسفر میپردازیم. فشاری که توسط هوای اطراف به یک جسم وارد میشود، فشار اتمسفریک (Atmospheric Pressure) یا فشار هوا نامیده میشود. از آنجا که اتمسفر زمین با هوا پر شده است، پس این هوا با دریافت نیروی جاذبه زمین میتواند به تمام اجسام و سطوح روی زمین فشار وارد کند.
واحد مرسوم برای بیان فشار هوا، اتمسفر است که با atm نشان داده میشود. به فشار هوا، فشار اتمسفر یا فشار بارومتریک هم گفته میشود. در بخش اول گفتیم که مقدار این فشار، تقریبا عدد ثابتی است و برابر است با:
همانطور که ملاحظه میکنید، فشار هوا عدد بزرگی است. یک اتمسفر همان متوسط فشار هوا در سطح دریا و در دمای ۱۵ C است. با توجه به بزرگی مقدار فشار هوا، ممکن است این سوال برای شما بوجود بیاید که چرا بدن ما فشاری با این مقدار را حس نمیکند؟
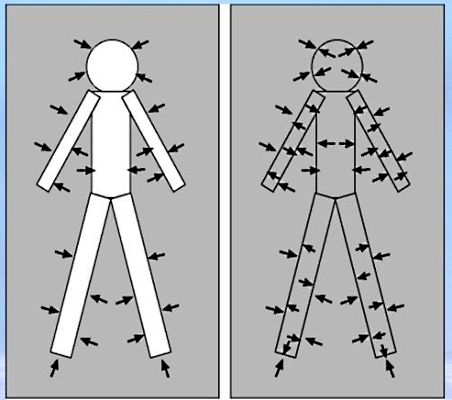
پاسخ این است که در داخل بدن انسان نیز فشاری برابر با مقدار فشار اتمسفر وجود دارد. در نتیجه برآیند اثر این دو فشار روی بدن صفر است و به همین علت است که بدن ما فشار هوا را حس نمیکند. مقدار فشار اتمسفر با توجه به افت و خیزهایی که در اتمسفر وجود دارد یا بر اثر تغییرات دمایی، متغیر است ولی عامل تعیینکننده در مقدار این نوع فشار، وزن هوا است. در بخش بعد توضیح میدهیم که چگونه میتوانیم با بررسی آزمایش توریچلی فشار هوا را اندازه بگیریم.
بارومتر چیست؟
اگر بخواهیم بهتر متوجه شویم تفاوت نحوه اندازهگیری فشار اتمسفر با فشار پیمانه ای چیست، بهتر است با طرز کار وسیله اندازهگیری آن دقیقتر آشنا شویم. بارومتر جیوهای وسیلهای است که برای اندازهگیری فشار اتمسفر بکار میرود و از یک لوله حاوی جیوه تشکیل شده است. این لوله ابتدا در داخل تشت پر از جیوه قرار دارد و سپس با برعکس شدن ناگهانی و قرار گرفتن بهصورت عمود طبق شکل زیر، در قسمت بالای آن خلاء شکل میگیرد.
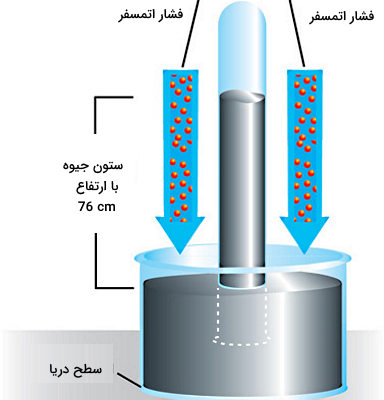
با وارد شدن فشار هوا به سطح جیوه داخل تشت (پیکانهای آبی)، جیوه در لوله بالا میرود. پس از اینکه جیوه به تعادل رسید و سطح آن در لوله تغییر نکرد، با استفاده از قوانین فشار در شارهها میتوانیم بگوییم فشار ستون جیوه با فشار هوا برابر است. به همین دلیل ارتفاع جیوه در لوله دیگر تغییری نمیکند. بنابراین فشاری که بارومتر بهعنوان فشار اتمسفر اندازهگیری میکند، از فرمول زیر به دست میآید:
در رابطه بالا ρ چگالی جیوه بر حسب کیلوگرم بر متر مکعب (kg/m3)، g شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه (m/s2) و h ارتفاع ستون جیوه در بارومتر بر حسب متر (m) است. چگالی جیوه را میدانیم و شتاب جاذبه هم معلوم است. پس کافی است ارتفاع ستون جیوه در لوله را از سطح جیوه در تشت اندازهگیری کنیم که برابر میشود با ۷۶ cm. با قرار دادن این اعداد، مقدار فشار هوا میشود.
نکته: طبق اندازهگیری بارومتر، میتوانیم بگوییم تبدیل فشار هوا از واحد پاسکال به واحد میلیمتر جیوه با رابطه زیر انجام میشود:
انواع دیگر فشار چیست؟
در توضیحات بخش اول دیدیم که برای اینکه بهتر متوجه شویم مفهوم فشار پیمانه ای چیست، لازم است انواع دیگر فشار، مانند فشار مطلق یا فشار اتمسفر را نیز بشناسیم. بهطور کلی انواع فشار بهصورت زیر طبقهبندی میشوند:

- فشار اتمسفر
- فشار مطلق
- فشار پیمانه ای
- فشار دیفرانسیلی
- فشار محیط
- فشار خلاء
با سه نوع فشار اول آشنا شدیم. در ادامه انواع دیگر فشار را بهصورت مختصر توضیح میدهیم.
فشار محیط
فشار محیط یا Ambient Pressure، اصطلاحی است که برای بیان فشار وارد شده از سمت هر نوع محیطی به یک جسم بکار میرود. محیط اطراف یک جسم میتواند شامل مایع، گاز یا هر نوع محیط دیگری باشد.
فشار خلاء
در بخشهای قبل یاد گرفتیم علت منفی شدن فشار پیمانه ای چیست و چه نام دارد. در خلاء کامل، فشار صفر است. معمولا از خلاء کامل برای تعریف فشار مطلق استفاده میشود، به این صورت که فشار مطلق در خلاء کامل برابر با صفر است. اما در واقعیت دستیابی به خلاء کامل مشکل است. اگر فشار یک سیستم از مقدار فشار هوا کمتر شود، در این صورت خلاء ایجاد میشود و فشار پیمانه ای در این شرایط همان فشار خلاء است.
فشار دیفرانسیلی
فشار دیفرانسیلی برابر است با هر نوع اختلاف فشاری که از کم کردن یک مقدار فشار از دیگری بهدست میآید:
اگر دقت کنید، فشار پیمانه ای هم نوعی اختلاف فشار یا فشار دیفرانسیلی محسوب میشود. اما هر نوع فشار دیفرانسیلی لزوما فشار پیمانه ای نیست.
یادگیری فشار در سیالات با فرادرس
در این نوشته آموختیم که فشار پیمانه ای چیست و با حل مثال و تمرین به توضیح چگونگی محاسبه آن پرداختیم. مسائلی که حل کردیم، در حوزه سیالات ساکن قرار میگیرند، در حالی که مباحث مربوط به دینامیک سیالات پیچیدهتر است. اگر تمایل دارید در این زمینه، یعنی «مکانیک سیالات» که جزء دروس اصلی رشته مهندسی مکانیک محسوب میشود، اطلاعات خوبی در قالب صدا و تصویر بهدست آورید، فیلمهای آموزشی زیر از فرادرس را ببینید:
- فیلم آموزش فیزیک پایه ۳ فرادرس
- فیلم آموزش فیزیک ۳ حل تمرین فرادرس
- فیلم آموزش مکانیک سیالات ۱ فرادرس
- فیلم آموزش مکانیک سیالات ۱ مرور و حل تمرین فرادرس
- فیلم آموزش مکانیک سیالات مرور و حل تست کنکور ارشد فرادرس
- فیلم آموزش مقدماتی مکانیک سیالات ۲ فرادرس
جمعبندی
در این مطلب از مجله فرادرس یاد گرفتیم فشار پیمانه ای چیست و چه تفاوتهایی با انواع دیگر فشار از جمله فشار مطلق دارد. همچنین نحوه محاسبه این فشار را در موقیعتهای مختلف با حل مثال و تمرین آموختیم. فشار پیمانه ای فشاری است که معمولا در فشارسنجها اندازهگیری میشود و مبدا آن فشار اتمسفر است. تفاوت مهمی که فشار پیمانه ای با فشار مطلق دارد در این است فشار مطلق نسبت به خلاء کامل سنجیده میشود.
برای پیدا کردن فشار پیمانه ای کافی است فشار جو را از فشار مطلق کم کنیم: . همچنین باید دقت کنیم که اگر فشار اندازهگیری شده سیستم از فشار جو کمتر باشد، در این صورت فشار پیمانه ای مقداری منفی دارد که فشار خلاء نامیده میشود.












