فرمول نیرو چیست؟ – محاسبه نیرو به زبان ساده
نیرو یکی از مهمترین مباحث فیزیک است. بر طبق قانون دوم نیوتن، نیرو برابر با حاصلضرب جرم جسم در شتاب حرکت آن است و با واحد نیوتن اندازهگیری میشود. بنابراین، با دانستن جرم و شتاب، نیرو به دست خواهد آمد. در این مطلب از مجله فرادرس، ابتدا با فرمول نیرو در حالت کلی آشنا میشوید. در ادامه، فرمول نیروهای مختلف همراه با حل مثالهای گوناگون آموزش داده خواهد شد.


فرمول نیرو چیست ؟
بر طبق قانون دوم نیوتن، نیرو از حاصلضرب جرم در شتاب به دست میآید. واحد شتاب، متر بر مجذور ثانیه یعنی است. واحد جرم نیز کیلوگرم است. در نتیجه، واحد نیرو برابر یا نیوتن است. به مثال ساده زیر توجه کنید.
مثال ۱
مریم در تلاش است جعبهای به جرم ۲ کیلوگرم را از زمین بلند کند و بر روی قفسه قرار دهد. اگر جعبه با شتاب دو متر بر مجذور ثانیه جابجا شود، نیروی وارد شده از طرف مریم بر جعبه را به دست آورید.
پاسخ
برای حل این مثال، جرم جعبه را در شتاب حرکت آن ضرب کنید.
جرم جعبه × شتاب حرکت جعبه = نیروی وارد شده بر جعبه
نیوتن ۴ = ۲ × ۲ = نیروی وارد شده بر جعبه
بنابراین، نیرویی که مریم بر جعبه وارد میکند برابر با چهار نیوتن است.
ذکر این نکته مهم است که در فیزیک، تمام کمیتها واحد یا یکا دارند. در این مطلب، در مورد انواع نیروهای موجود در طبیعت و فرمول مربوط به آنها با ذکر مثالها گوناگون صحبت میکنیم. لیست این نیروها همراه با فرمول در جدول زیر ارائه شده است.
| نام نیرو | فرمول نیرو |
| نیروی وزن |
m = جرم جسم g = شتاب جاذبه در سطح زمین |
| نیروی اصطکاک |
نیروی اصطکاک ایستایی = نیروی اصطکاک جنبشی= = ضریب اصطکاک ایستایی = ضریب اصطکاک جنبشی N = نیروی عمودی سطح |
| نیروی الکتریکی |
= بار الکتریکی جسم ۱ = بار الکتریکی جسم ۲ = فاصله بین دو جسم k = ثابت تناسب یا ثابت قانون کولن |
| نیروی مغناطیسی |
q = بار الکتریکی ذره متحرک در میدان مغناطیسی v = سرعت حرکت ذره باردار در میدان مغناطیسی B = میدان مغناطیسی = زاویه بین سرعت ذره با میدان مغناطیسی |
| نیروی گریز از مرکز یا مرکزگرا |
m = جرم جسم v = سرعت حرکت جسم r = شعاع مسیر دایرهای |
| نیروی شناوری |
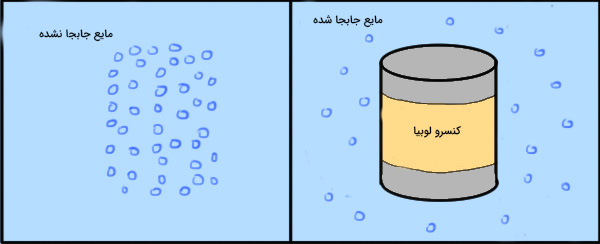
= چگالی شارهای که جسم در آن قرار گرفته است. g = شتاب جاذبه در سطح زمین = حجم مایع یا شاره جابجا شده |
| نیرو محرکه القایی |
= نیرو محرکه القایی E = انرژی موجود در مدار Q = بار موجود در مدار I = جریان = نیرو محرکه القایی R = مقاومت مدار r = مقاومت داخلی باتری |
| نیرو مقاومت هوا |
F = نیروی ناشی از مقاومت هوا k = ضریب ثابتی که شامل چگالی، ضریب درگ و مساحت است. v = سرعت حرکت جسم = چگالی هوا = ضریب درگ A = مساحت تماس جسم با هوا |
به دست آوردن کمیت های دیگر
با استفاده از فرمول نیرو میتوان کمیتهای دیگر را نیز به دست آورد. به عنوان مثال، با داشتن مقدارهای جرم و نیرو، شتاب حرکت را میتوان محاسبه کرد. اگر در درک این موضوع کمی مشکل دارید استفاده از دایره نشان داده شده در تصویر زیر بسیار مفید خواهد بود.

ابتدا دایرهای رسم کنید. سپس، با رسم خطی افقی دایره را به دو قسمت مساوی تقسیم کنید. نیمه پایینی دایره را با رسم خطی عمودی به دو بخش تقسیم کنید. F یا نیرو را در نیمه بالایی دایره بنویسید. جرم یا m را در یکی از قسمتهای پایینی دایره و شتاب یا a را در قسمت دیگر یادداشت کنید. در این دایره، خط افقی نشاندهنده تقسیم و خط عمودی بیانکننده ضرب است.
به هنگام حل مساله، کمیت مجهول یا خواسته شده را با انگشت بپوشانید. به عنوان مثال، فرض کنید کمیت خواسته شده شتاب است. بنابراین، انگشت خود را بر روی a قرار دهید (تصویر نشان داده شده در ادامه). تنها F و m باقی ماندهاند. F در بالای خط افقی و m پایین آن قرار گرفتهاند. در نتیجه، برای به دست آوردن شتاب، نیرو را بر جرم تقسیم میکنیم.

مثال ۲
عمه علی میخواهد زیر آفتاب بنشیند. علی صندلی به جرم ۳۰۰ کیلوگرم را با نیرویی برابر ۳۰۰ نیوتن هل میدهد. شتاب حرکت صندلی را به دست آورید.
پاسخ
برای حل این مثال از دایره نشان داده شده در بالا استفاده میکنیم. شتاب را با دست میپوشانیم و نیرو را بر جرم صندلی تقسیم میکنیم. در نتیجه، شتاب حرکت آن مقداری برابر یک متر بر مجذور ثانیه به دست میآید.
تا اینجا فرض کردیم که تنها یک نیرو بر جسم وارد میشود. در صورتی که نیروهای مختلفی بر آن وارد شوند مساله چگونه حل میشود؟
وارد شدن نیروهای مختلف بر جسم
در ابتدا ذکر این نکته مهم است که نیرو کمیتی برداری و دارای اندازه و جهت است. بنابراین، اگر تعداد N نیروی مختلف بر جسمی وارد شوند، نیروی کلی وارد شده بر آن برابر با جمع برداری نیروهای اعمال شده است.
در رابطه بالا ، و ... نیروهای وارد شده بر جسم هستند. به نیروی F، نیروی کل یا نیروی خالص وارد شده بر جسم گفته میشود. بر طبق قانون دوم نیوتن، نیروی کل وارد شده سبب حرکت جسم با شتاب معینی خواهد شد.
در توضیحات بالا، فرمول نیرو برای حالتی که تنها یک نیرو بر جسم وارد شود به دست آورده شد. هنگامی که نیروهای مختلفی بر جسم وارد شوند نیز حالت مشابهی برقرار است. بزرگی نیروی کل وارد شده بر هر جسمی برابر حاصلضرب جرم جسم در شتاب حرکت آن است.
اگر نیروی کل وارد شده بر جسم برابر صفر باشد، شتاب حرکت آن برابر صفر خواهد بود. در این حالت، جسم در تعادل است. برای جسم در حال تعادل دو اتفاق ممکن است رخ بدهد:
- جسم در حالت سکون قرار دارد.
- با سرعت ثابت در حال حرکت است.
در ادامه، با چگونگی به دست آوردن نیروی کل وارد شده بر جسم آشنا میشویم.
محاسبه نیروی کل
برای به دست آوردن نیروی کل وارد شده بر جرم، به نکتههای زیر دقت کنید:
- ابتدا جهت نیروی وارد شده را تعیین کنید. این جمله بدان معنا است که افقی یا عمودی بودن نیروی وارد شده را باید تعیین کنیم. همچنین، باید زاویه بین نیرو با محورهای افقی (x) یا عمودی (y) را بدانیم.
- اگر نیرو با محورهای افقی یا عمودی زاویه ساخته بود، باید مولفههای آن را با توجه به تجزیه بردارها به دست آوریم.
- با توجه به جمع و تفریق بردارها، مولفههای نیروی کل را در راستای x و y به دست میآوریم. ذکر این نکته مهم است، که بردارهای موازی همجهت با یکدیگر جمع و بردارهای موازی خلاف جهت از یکدیگر کم میشوند.
تصویر زیر جمع برداری نیروهای مختلفی را نشان میدهد.
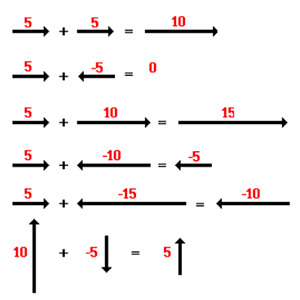
با توجه به تصویر فوق، نیروی وارد شده به سمت پایین، تمام یا قسمتی از نیروی اعمال شده به سمت بالا را خنثی میکند. همچنین، نیرویی که به سمت چپ وارد میشود، تمام یا قسمتی از نیروی وارد شده به سمت راست را خنثی خواهد کرد.
مثال اول محاسبه نیروی کل
تصویر زیر نیروهای وارد شده بر جسمی را در چهار حالت مختلف نشان میدهد. نیروی کل وارد شده بر جسم را در هر حالت به دست آورید.
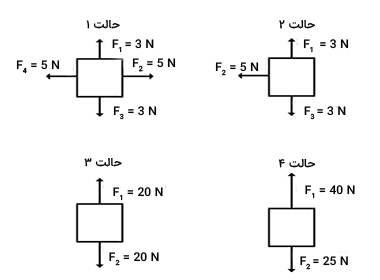
پاسخ
حالت (۱): در این حالت چهار نیرو شامل دو نیروی افقی و دو نیروی عمودی بر جسم وارد شدهاند. نیروهای عمودی و افقی در خلاف جهت یکدیگر قرار گرفتهاند. با توجه به آنکه اندازه دو نیروی عمودی با یکدیگر و دو نیروی افقی با هم برابر هستند، در نتیجه جمع برداری آنها برابر صفر خواهد بود. در نیجه نیروی کل وارد شده بر جسم برابر صفر است.
حالت (۲): در این حالت دو نیرو در جهت عمودی و یک نیرو در جهت افقی بر جسم وارد شده است. اندازه دو نیروی عمودی با یکدیگر برابر و خلاف جهت یکدیگر هستند. در نتیجه، جمع برداری آنها برابر صفر است. تنها نیروی اعمال شده بر جسم، نیروی افقی با اندازه ۵ نیوتن و به سمت چپ است. آیا میدانید جسم در چه جهتی حرکت میکند؟ جعبه به سمت چپ حرکت خواهد کرد. زیرا نیروی کل وارد شده بر آن، افقی و جهت آن به سمت چپ است.
حالت (۳): در این حالت، تنها دو نیروی عمودی با اندازههای 20 نیوتن بر جعبه وارد شدهاند. اما از آنجایی که این دو نیرو در خلاف جهت یکدیگر قرار دارند، نیروی کل وارد شده بر جعبه برابر صفر خواهد بود.
حالت (۴): در این حالت نیز دو نیروی عمودی با اندازههای متفاوت بر جسم وارد شدهاند. در نتیجه، نیروی کل وارد شده بر جسم برابر 15 نیوتن و جهت آن به سمت بالا است.
مثال دوم محاسبه نیروی کل
نیروهای وارد شده بر جعبهای در چهار حالت مختلف در تصویر زیر نشان داده شده است. نیروی کل برای هر حالت داده شده است. مقدار نیروهای مجهول را برای هر حالت به دست آورید.
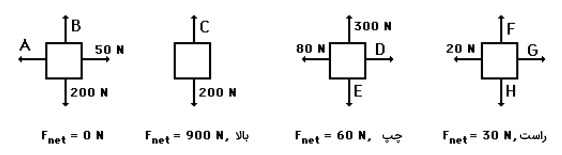
پاسخ
برای حل این مثال جهت بالا و جهت راست را مثبت در نظر میگیریم.
حالت (۱): در حالت ۱، اندازه نیروی کل برابر صفر است. در نتیجه، جمع نیروهای وارد شده در جهت افقی و عمودی برابر صفر خواهد بود. بنابراین داریم:
حالت (۲): در حالت ۲، اندازه نیروی کل وارد شده بر جعبه برابر ۹۰۰ نیوتن و جهت آن به سمت بالا است.
حالت (۳): در این حالت، اندازه نیروی کل وارد شده بر جسم برابر ۶۰ نیوتن و جهت آن به سمت چپ است. از آنجایی که جهت نیروی کل افقی و به سمت چپ است، نیروهای عمودی یکدیگر را خنثی خواهند کرد. در نتیجه اندازه نیروی E برابر ۳۰۰ نیوتن خواهد بود. برای نیروی D داریم:
حالت (۴): در حالت ۴، اندازه نیروی کل وارد شده بر جعبه برابر ۳۰ نیوتن و جهت آن به سمت راست است. در نتیجه، برای نیروی G داریم:
دو نیروی F و G نیز با یکدیگر برابر هستند و اندازه آنها هر مقداری دلخواهی خواهد بود.
تاکنون به پرسش فرمول نیرو چیست در حالت کلی پاسخ دادیم.
در طبیعت نیروهای مختلفی وجود دارد. اولین و مهمترین نیرویی که بر هر جسمی بر روی سطح زمین وارد میشود، نیروی وزن ناشی از جاذبه زمین است. نیروی مهم دیگر نیروی اصطکاک است. اگر جسمی بر روی سطح زبری حرکت کند، نیرویی در خلاف جهت حرکت از طرف سطح بر آن وارد میشود.
اگر جسم بارداری در میدان الکتریکی خارجی قرار بگیرد، از سمت میدان الکتریکی بر آن نیرویی وارد خواهد شد. جهت نیروی وارد شده به مثبت یا منفی بودن بار جسم بستگی دارد. نیروهای مغناطیسی، نیروی گرانشی، نیروی گریز از مرکز، نیروی شناوری و نیروی محرکه القایی نیز از جمله نیروهای مهم دیگری هستند که در ادامه فرمول و نحوه محاسبه آنها شرح داده میشود.
فرمول نیروی وزن چیست ؟
هر جسمی را رها یا به سمت بالا پرتاب کنید، به سمت زمین برمیگردد. چه عاملی باعث برگشت اجسام به سمت زمین میشود؟ پاسخ به این پرسش، نیروی جاذبه است. به اندازه نیروی جاذبه که سبب کشش اجسام به طرف زمین میشود، وزن میگوییم.
نیروی وزن به دو عامل بستگی دارد:
- جرم: مقدار ماده تشکیل دهنده اجسام.
- شتاب رو به پایین جسم به دلیل جاذبه.
ذکر این نکته مهم است که اندازه شتاب جاذبه در همه جای زمین یکسان است.
همانگونه که در مطالب بالا عنوان شد، فرمول نیرو در حالت کلی به صورت زیر نوشته میشود:
در رابطه بالا، به جای a، شتاب جاذبه را قرار میدهیم. شتاب جاذبه با حرف g نشان داده میشود و مقدار آن برابر ۹/۸۰ متر بر مجذور ثانیه است. در نتیجه، فرمول نیرو براب وزن به صورت زیر نوشته میشود:
محاسبه وزن
تمام اجسام بر روی زمین به دلیل جاذبه به سمت پایین شتاب میگیرند. بنابراین، با دانستن جرم جسم، وزن آن به راحتی به دست خواهد آمد:
مثال ۱: اگر جرم شما برابر ۵۰ کیلوگرم باشد، وزن خود را بر حسب نیوتن به دست آورید.
پاسخ: با جایگذاری جرم در رابطه بالا، وزن به دست میآید:
مثال ۲: اگر وزن فردی بر روی ماه برابر ۵۰۰ نیوتن باشد، جرم او را به دست آورید. مقدار شتاب جاذبه بر روی سطح ماه برابر ۱/۶۲ متر بر مجذور ثانیه است.
پاسخ: برای حل این مثال از دایره گفته شده در ابتدای متن استفاده میکنیم. مقدار مجهول در اینجا، جرم فرد است. در نتیجه، انگشت خور را بر روی جرم قرار میدهیم. با تقسیم کردن نیروی وزن بر شتاب جاذبه، جرم فرد به دست خواهد آمد:
اگر جسمی بر روی سطح زبری حرکت کند، از طرف سطح نیرویی به نام نیروی اصطکاک در خلاف جهت حرکت به آن وارد میشود. در ادامه در مورد فرمول نیرو برای اصطکاک و محاسبه آن توضیح میدهیم.
فرمول نیروی اصطکاک چیست ؟
در حالت کلی فرمول نیرو برای اصطکاک به صورت حاصلضرب نیروی عمودی سطح در ضریب اصطکاک تعریف میشود. در ادامه، ابتدا نیروی اصطکاک و انواع آن و همچنین محاسبه این نیرو با حل مثالهای مختلف، توضیح داده میشود.
نیروی اصطکاک چیست ؟
نیروی اصطکاک به دو نوع ایستایی و جنبشی تقسیم میشود. نیروی اصطکاک ایستایی () نیروی بین دو سطح است که از لغزش یا لیز خوردن این سطوح بر روی یکدیگر جلوگیری میکند. این حالت مشابه نیرویی است که به شما در هنگام دویدن، شتاب رو به جلو میدهد. به دلیل وجود نیروی اصطکاک ایستایی سطوح بر روی یکدیگر نمیلغزند. اگر هیچ نیروی اصطکاکی بین پای شما و زمین وجود نداشت، دویدن غیرممکن بود و در همان مکان اولیه در جا میزدید (مانند دویدن بر روی سطوح یخزده).
اگر دو سطح بر روی یکدیگر بلغزند، نیروی اصطکاک بین آنها نیروی اصطکاک جنبشی () خواهد بود. نیروی اصطکاک جنبشی همواره مخالف حرکت لغزشی دو سطح و در تلاش برای کاهش سرعت لغزش سطوح بر روی یکدیگر است.

فرمول نیرو برای نیروی اصطکاک جنبشی چیست ؟
اگر دستان خود را محکم به یکدیگر بمالید، نیروی اصطکاک جنبشی بزرگتر از حالتی خواهد بود که دستان خود را آهسته به یکدیگر میمالید. این به دلیل آن است که نیروی اصطکاک جنبشی بین دو سطح، هنگامی که محکم به هم فشار داده میشوند بزرگتر خواهد بود (نیروی عمودی سطح بزرگتر است).
اگر نوع یا جنس سطح تغییر کند، بزرگی نیروی اصطکاک جنبشی نیز تغییر خواهد کرد. زبری بین دو سطحی که بر روی یکدیگر میلغزند با کمیتی به نام ضریب اصطکاک جنبشی یا مشخصهیابی میشود. این کمیت تنها به سطوح در تماس بستگی دارد و مقدار آن برای سطوح متفاوت، تغییر خواهد کرد (به عنوان مثال چوب و یخ یا آهن و سیمان). مقدار ضریب اصطکاک جنبشی برای دو سطحی که به سختی بر روی یکدیگر میلغزند، بزرگتر خواهد بود.

با توجه به توضیحات فوق، فرمول نیرو برای اصطکاک جنبشی به صورت زیر نوشته میشود:
رابطه بالا به صورت زیر نیز نوشته میشود:
در نتیجه، ضریب اصطکاک جنبشی بدون بعد است.
فرمول نیرو برای نیروی اصطکاک ایستایی چیست ؟
نیروی اصطکاک ایستایی کمی با نیروی اصطکاک جنبشی متفاوت است. مقدار نیروی اصطکاک ایستایی به توجه به اندازه نیروی وارد شده بر جسم ساکن، تغییر خواهد کرد. به عنوان مثال، تصور کنید در تلاش برای حرکت جعبهای بر روی سطح سیمانی هستید. ممکن است نیروی زیادی بر جعبه وارد کنید، اما نتوانید آن را حرکت دهید. در این صورت، نیروی اصطکاک ایستایی به نیروی وارد شده از سمت شما بر جعبه، پاسخ داده است.
هر چقدر نیروی اعمال شده بر جعبه افزایش یابد، نیروی اصطکاک ایستایی در جهت مخالف افزایش خواهد یافت. ناگهان در یک لحظه حس میکنید که جعبه از حالت سکون شروع به حرکت میکند. در این هنگام، حفظ حرکت راحتتر از شروع حرکت است. در نتیجه، مقدار نیروی اصطکاک جنبشی کمتر از بیشینه نیروی اصطکاک ایستایی خواهد بود.
اگر بر روی جعبه موردنظر آجری قرار دهید (افزایش نیروی عمودی سطح)، برای به حرکت درآوردن و حفظ حرکت آن نیازمند اعمال نیروی بیشتری خواهید بود. همچنین، اگر بر روی سطح سیمانی روغن بریزید (کاهش ضریب اصطکاک ایستایی)، به حرکت درآوردن جعبه بسیار راحتتر خواهد بود. با توجه به نکات بیان شده، بیشینه نیروی اصطکاک ایستایی به صورت زیر نوشته می شود:
توجه به این نکته مهم است که تنها مقدار بیشینه ممکن برای نیروی اصطکاک ایستایی را میدهد. مقدار واقعی این نیرو با استفاده رابطه فوق به دست نمیآید. به عنوان مثال، فرض کنید مقدار نیروی اصطکاک ایستایی بیشینه بین کف آشپزخانه و ماشین لباسشویی برابر 50 نیوتن است.
اگر برای به حرکت درآوردن ماشین لباسشویی بر آن نیروی 30 نیوتن وارد کنید، مقدار نیروی اصطکاک ایستایی نیز برابر 30 نیوتن خواهد بود. اگر مقدار نیروی اعمالی برابر ۴۰ نیوتن باشد، اندازه نیروی اصطکاک ایستایی نیز به ۴۰ نیوتن افزایش خواهد یافت. افزایش اندازه نیروی اصطکاک ایستایی تا جایی ادامه پیدا میکند که نیروی اعمال شده از 50 نیوتن بیشتر شود. در این هنگام، ماشین لباسشویی شروع به حرکت خواهد کرد. به محض به حرکت درآمدن ماشین لباسشویی، تنها نیروی بین سطوح، نیروی اصطکاک جنبشی است.
محاسبه نیروی اصطکاک
تاکنون با فرمول نیرو برای اصطکاک ایستایی و جنبشی آشنا شدید. در ادامه، با حل مثالهایی، چگونگی استفاده از این فرمولها توضیح داده خواهد شد.
مثال اول فرمول نیروی اصطکاک
یخچالی به جرم ۱۱۰ کیلوگرم در آشپزخانه قرار دارد. ضریب اصطکاک ایستایی و جنبشی بین یخچال و کف آشپزخانه به ترتیب برابر ۰/۶۰ و ۰/۴۰ هستند. شخصی با سه نیروی داده شده در ادامه، یخچال را هل میدهد.
- ۴۰۰ نیوتن
- ۶۰۰ نیوتن
- ۸۰۰ نیوتن
برای هر یک از نیروهای داده شده، اندازه نیروی اصطکاک بین کف یخچال و زمین را به دست آورید.
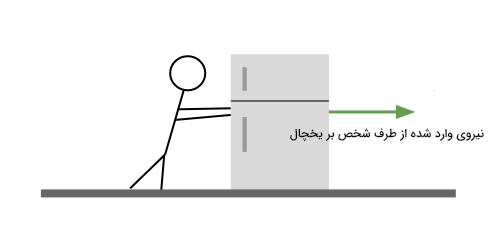
پاسخ
برای شروع، بیشینه مقدار نیروی اصطکاک ایستایی را به دست میآوریم:
مقدار نیروی عمودی سطح برابر نیروی وزن یخچال است. در نتیجه داریم:
با جایگذاری مقادیر داده شده در رابطه فوق داریم:
اکنون مقدار بیشینه نیروی اصطکاک ایستایی را میدانیم.
حالت (۱): در این حالت شخص با نیرویی برابر ۴۰۰ نیوتن یخچال را هل میدهد. این مقدار از مقدار بیشینه نیروی اصطکاک ایستایی یعنی ۶۴۷ نیوتن کمتر است. در نتیجه، یخچال از جای خود حرکت نخواهد کرد و مقدار نیروی اصطکاک ایستایی برابر ۴۰۰ نیوتن است.
حالت (۲): شخص با نیروی بیشتری، یعنی ۶۰۰ نیوتن، یخچال را هل می دهد. همچنان اندازه این نیرو کمتر از بیشینه نیروی اصطکاک ایستایی خواهد بود. در نتیجه یخچال در مکان خود ساکن میماند و مقدار نیروی اصطکاک ایستایی برابر ۶۰۰ نیوتن است.
حالت (۳): در این حالت شخص یخچال را با نیرویی برابر ۸۰۰ نیوتن هل میدهد. اندازه نیروی وارد شده از بیشینه نیروی اصطکاک ایستایی بیشتر خواهد بود. در نتیجه، یخچال شروع به حرکت میکند و نیروی وارد شده بین سطوح از نوع اصطکاک جنبشی است. اندازه این نیرو به صورت زیر محاسبه میشود:
مثال دوم فرمول نیروی اصطکاک
جعبهای به جرم ۱/۳ کیلوگرم با استفاده از طناب بر روی سطح میزی با سرعت ثابت حرکت میکند. طناب با سطح افقی زاویه ۶۰ درجه ساخته است و نیروی کشش آن برابر ۴ نیوتن است. ضریب اصطکاک ایستایی جنبشی بین میز و جعبه را به دست آورید.
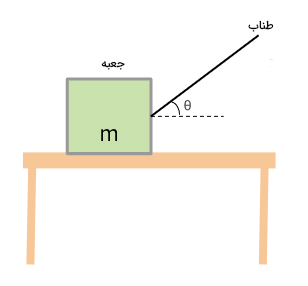
پاسخ
از آنجایی که مقدار ضریب اصطکاک جنبشی را نمیدانیم، از فرمول استفاده نمیکنیم. اما مقدار شتاب در راستای افقی را میدانیم. همچنین، جعبه با سرعت ثابتی حرکت میکند، در نتیجه مقدار شتاب برابر صفر خواهد بود. بنابراین، برای حل این مثال از قانون دوم نیوتن استفاده میکنیم.
به هنگام استفاده از قانون دوم نیوتن، از نمودار جسم آزاد استفاده و تمام نیروهای وارد بر جسم را مشخص میکنیم:
- نیروی وزن به سمت پایین
- نیروی کشش طناب (ُT)
- نیروی عمودی سطح به سمت بالا
نیروی کشش طناب با راستای افقی زاویه ۶۰ درجه ساخته است. در نتیجه، T را در دو راستای x و y به صورت زیر تجزیه میکنیم:
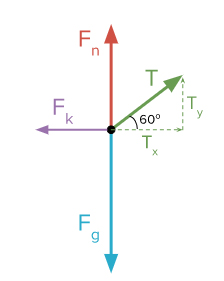
بر طبق قانون دوم نیوتن در راستای محور x داریم:
همانگونه که گفتیم، مقدار شتاب در راستای افقی برابر صفر است. در نتیجه داریم:
با قرار دادن مقدار نیروی کشش طناب در راستای افقی در رابطه بالا داریم:
اکنون باید مقدار نیروی عمودی سطح را به دست آوریم. آیا مقدار آن برابر نیروی وزن یعنی mg است؟ پاسخ به این پرسش خیر است. زیرا نیروی کشش طناب نیز مولفهای در راستای عمودی و به سمت بالا خواهد داشت. در نتیجه، اندازه N کمتر از mg است.
در نتیجه، برای ضریب اصطکاک جنبشی داریم:
تاکنون با فرمول نیرو برای نیروهای وزن و اصطکاک آشنا شدیم. در ادامه، فرمول نیرو را برای نیروهای الکتریکی و مغناطیسی با حل مثالهای مختلف توضیح میدهیم.
فرمول نیروی الکتریکی چیست ؟
برهمکنش بین اجسام باردار از نوع نیروی غیرتماسی است که تا فاصله مشخصی وارد میشود. به این سه کلمه دقت کنید:
بار، بار و فاصله
هر برهمکنش الکتریکی شامل نیرویی است که به سه کلمه بیان شده در بالا وابسته است. جنس و نوع اجسام باردار مهم نیستند. مقدار و بزرگی برهمکنش الکتریکی به اندازه بار الکتریکی دو جسم و فاصله بین آنها بستگی دارد.
نیروی الکتریکی، مانند همه نیروها، کمیتی برداری است و با واحد نیوتن اندازهگیری میشود. جهت نیروی الکتریکی به همنام یا غیرهمنام بودن بار الکتریکی دو جسم و جهتگیری فضایی آنها بستگی دارد. با دانستن نوع بار الکتریکی دو جسم، جهت نیروی الکتریکی وارد شده بر یکی از اجسام تعیین خواهد شد. در تصویر زیر، اجسام A و B بار الکتریکی یکسانی دارند. در نتیجه، یکدیگر را دفع میکنند. بنابراین، نیروی وارد شده بر جسم A به سمت چپ و نیروی وارد شده بر جسم B به سمت راست است.
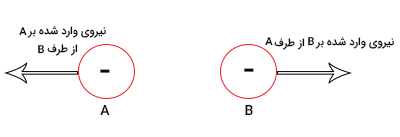
اکنون دو جسم C و D با بارهای غیریکسان را در نظر بگیرید. این دو جسم یکدیگر را جذب میکنند. بنابراین، نیروی وارد شده بر جسم C به سمت راست و به سمت جسم D است. همچنین، نیروی وارد شده بر جسم D به سمت چپ و به سمت جسم C خواهد بود.
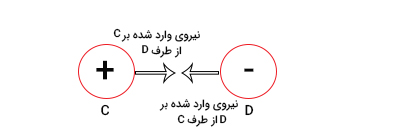
نیروی الکتریکی علاوه بر جهت دارای اندازه نیز است. فاکتورهای مشخصی بر اندازه این نیرو تاثیر میگذارند. دو جسم با بار الکتریکی همسان یکدیگر را دفع میکنند. سه عامل بر اندازه نیروی بین آنها تاثیر خواهد گذاشت.
- اندازه بار جسم A بر بزرگی نیروی دافعه تاثیر میگذارد. هر اندازه بار الکتریکی آن بزرگتر باشد، نیروی دافعه بین A و B نیز بزرگتر خواهد بود.
- اندازه بار جسم B نیز بر بزرگی نیروی دافعه تاثیر میگذارد. همانند مورد ۱، هر اندازه بار الکتریکی آن بزرگترباشد، نیروی دافعه بین A و B نیز بزرگتر خواهد بود.
- فاصله بین دو جسم A و B تاثیر بسزایی بر اندازه نیروی دافعه خواهد داشت. اندازه نیروی دافعه هنگامی که دو جسم در نزدیکترین فاصله از یکدیگر قرار دارند، بیشترین مقدار خواهد بود. در واقع، اندازه نیروی دافعه با فاصله بین دو جسم نسبت عکس دارد.
قانون کولن
در توضیحات بالا بیان شد که نیروی الکتریکی به اندازه با دو جسم و فاصله بین آنها بستگی دارد. بیان ریاضی این موضوع به عنوان قانون کولن شناخته میشود. بر طبق این قانون، نیروی الکتریکی بین دو جسم باردار با حاصلضرب اندازه بار الکتریکی دو جسم نسبت مستقیم و با مجذور فاصله بین آنها نسبت عکس دارد. بیان ریاضی این قانون به صورت زیر نوشته میشود:
اندازه بار جسم ۱ =
اندازه بار جسم ۲ =
فاصله بین دو جسم بر حسب متر = d
ثابت تناسب یا ثابت قانون کولن = k
مقدار k به محیطی که بارهای الکتریکی در آن قرار گرفتهاند بستگی دارد. اگر محیط هوا باشد، مقدار آن در حدود است. اگر بارهای الکتریکی در آب باشند، مقدار k در حدود ۸۰ برابر کوچکتر خواهد شد.
هرگاه دو جسم باردار به صورت ذرات نقطهای در نظر گرفته شوند، معادله قانون کولن توصیف دقیقی از نیروی بین آنها ارائه خواهد داد. برهمکنش بین کرهای باردار با اجسام باردار دیگر به گونهای خواهد بود که گویا تمام بار الکتریکی کره در مرکز آن جمع شده است. از آنجایی که قانون کولن در مورد بارهای نقطهای صدق میکند، d فاصله بین مرکزهای اجسام است.
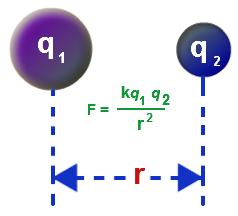
نمادهای و در معادله قانون کولن بیانگر اندازه بار الکتریکی دو جسم برهمکنش کننده هستند. از آنجایی که بار الکتریکی اجسام مثبت یا منفی است، این دو مقدار به صورت مقدارهای مثبت یا منفی بیان میشوند. در بیشتر مواقع، به هنگام محاسبه نیروی الکتریکی از اندازههای بارها بدون در نظر گرفتن علامت آنها استفاده میشود. در حالت کلی به یاد داشته باشید که:
- نیروی وارد شده بین بارهای همنام دافعه، و بین بارهای غیرهمنام جاذبه است.
نکته: قانون کولن شباهت بسیاری به قانون گرانش نیوتن دارد:
همانند نیروی گرانش که اندازه آن با جرم افزایش مییابد، اندازه نیروی الکتریکی نیز با اندازه بار الکتریکی افزایش خواهد یافت. هر دو نیرو در امتداد خط فرضی متصل کننده دو جسم، وارد میشوند. همچنین، اندازه این دو نیرو با مجذور فاصله بین دو جسم نسبت عکس دارد.
تفاوت اصلی نیروی گرانش و نیروی الکتریکی مقدارهای نسبی آنها است که به نسبت بین G به k مربوط میشود. نیروی الکترواستاتیکی بین الکترون و پروتون چندین مرتبه بزرگتر از نیروی گرانش بین آنها است.
مثال اول فرمول نیروی الکتریکی
دو بار الکتریکی یکسان در فاصله ۵ سانتیمتری از یکدیگر قرار گرفتهاند و بر یکدیگر نیرویی برابر وارد میکنند.
(۱) اندازه هر یک از بارهای الکتریکی را به دست آورید.
(۲) جهت نیروی الکترواستاتیکی بین آنها را تعیین کنید.
پاسخ
بزرگی نیروی بین دو بار ساکن q و 'q که در فاصله d از یکدیگر قرار گرفتهاند برابر است با:
در صورت مثال فرض شده است که اندازه دو بار یکسان است. در نتیجه داریم:
با جایگذاری مقدارهای داده شده در مثال داریم:
در رابطه بالا، r به متر تبدیل شده است.
جهت نیروی الکتریکی بستگی به علامت بارها دارد. از آنجایی که اندازه و علامت دو بار یکسان است، نیروی بین آنها دافعه خواهد بود.
مثال دوم فرمول نیروی الکتریکی
بار نقطهای q با اندازه در فاصله ۳ سانتیمتری از بار 'q با اندازه قرار گرفته است. اندازه نیروی الکتریکی بین دو بار را به دست آورید. این نیرو دافعه یا جاذبه است؟
پاسخ
مقدارهای معلوم عبارتند از:
با استفاده از قانون کولن، اندازه نیروی بین این دو بار را به دست میآوریم:
از آنجایی که علامت دو بار مخالف یکدیگر است، نیروی الکتریکی بین آنها جاذبه خواهد بود.
مثال سوم فرمول نیروی الکتریکی
دو ذره باردار بر یکدیگر نیروی الکتریکی به بزرگی وارد میکنند. اگر فاصله بین آنها دو برابر شود، اندازه نیروی وارد شده بر آنها چه مقدار خواهد شد؟
پاسخ
با استفاده از قانون کولن داریم:
r فاصله اولیه دو بار است. در ادامه دو بار از یکدیگر دور میشوند و در فاصله 'r از یکدیگر قرار میگیرند:
همانگونه که میدانیم، با افزایش فاصله بین دو بار، اندازه نیروی الکتریکی کاهش مییابد. بنابراین، داریم:
مثال چهارم فرمول نیروی الکتریکی
چهار بار الکتریکی در راسهای مربعی به طول قرار گرفتهاند. مقدار نیروی کل وارد شده بر بار q- را به دست آورید.
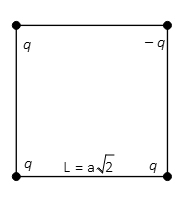
پاسخ
در ابتدا، نیروی الکتریکی وارد شده از طرف سه بار دیگر را بر بار q- به دست میآوریم. سپس، جمع برداری آنها را به حساب میکینم. اندازه بارهای الکتریکی و با یکدیگر برابر هستند و در فاصله یکسانی از بار قرار گرفتهاند. در نتیجه، اندازه نیروی الکتریکی وارد شده از سمت این دو بار بر بار برابر خواهند بود:
از آنجایی که دو بار علامتهای مخالف دارند، نیروی به سمت چپ و نیروی به سمت پایین خواهند بود (تصویر نشان داده شده در ادامه). در نتیجه، نیروی کل F حاصل از این دو نیرو برابر یا است.
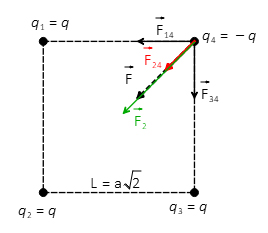
به طور مشابه، نیروی وارد شده از سمت بار را بر بار به دست میآوریم:
فاصله بین بارهای و برابر با قطر مربع است که با استفاده از قضیه فیثاغورث به دست میآید.
علامت بارهای و مخالف یکدیگر است. بنابراین، نیروی الکتریکی بین آنها جاذبه و جهت آن در امتداد قطر مربع و به سمت داخل است.
اندازه نیروی کل وارد شده بر بار برابر جمع برداری دو نیروی F و است. از آنجایی که این دو نیرو در یک امتداد و جهت قرار دارند، جمع آنها برابر جمع جبری اندازههای آنها خواهد بود.
مثال پنجم فرمول نیروی الکتریکی
دو بار الکتریکی و در فصله ۳۰ سانتیمتر از هم قرار گرفتهاند. بار q به گونهای قرار میگیرد که سه بار در حالت تعادل قرار بگیرند. اندازه و علامت بار q را به دست اورید.
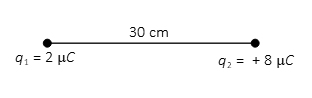
پاسخ
برای یافتن مکان بار سوم، به صورت آزمایشی بار مثبت یا منفی را در نقطهای مابین و قرار میدهیم. از آنجایی که همه بارها مثبت (منفی) هستند. بنابراین، بر طبق قانون کولن، نیروهای الکتریکی بر روی بار آزمایشی دافعه (جاذبه) و به سمت چپ (راست) و راست (چپ) آن خواهند بود. در این حالت، نیروی الکتریکی کل در فاصله x از بار صفر است.
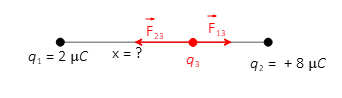
اکنون، نیروهای وارد شده از طرف بارهای و بر بار را مساوی یکدیگر قرار میدهیم:
در محاسبات فوق، بار از طرفین معادله حذف شد. در نتیجه، برای یافتن مقدار و علامت آن، نیروهای وارد شده بر بار را برابر قرار میدهیم:
نیروی نیروی دافعه و جهت آن در راستای منفی محور x است. از آنجایی که نیروی الکتریکی کل بر روی هر ۳ بار برابر صفر است، علامت بار باید منفی باشد. در این صورت، نیروی جاذبهای در خلاف جهت نیروی و در راستای مثبت محور x ایجاد خواهد شد.
فرمول نیروی مغناطیسی چیست ؟
به نیروی وارد شده بر جسمی که ناشی از برهمکنش آن با میدان مغناطیسی است، نیروی مغناطیسی میگوییم. در بیان کلی، این نیرو به صورت ضرب خارجی برداری سرعت جسم در میدان مغناطیسی تعریف میشود. مانند هر نیروی دیگری، واحد این نیرو نیز نیوتن است.
آیا تا به حال دو آهنربای دائمی را کنار یکدیگر نگه داشتهاید؟ اگر این کار را انجام دهید، وجود نیروی مغناطیسی را حس خواهید کرد. اگر قطبهای جنوب یا شمال را در نزدیکی یکدیگر قرار دهیم، نیروی مغناطیسی دافعه است و آهنرباها یکدیگر را در جهتهای مخالف دفع خواهند کرد. همچنین، قطبهای غیرهمنام یکدیگر را جذب میکنند.

منشا اصلی میدان مغناطیسی، بار متحرک است. در سطح میکروسکوپی، میدان مغناطیسی به دلیل حرکت الکترونها در اتمهای مواد مغناطیسی ایجاد میشود.
رابطه ریاضی نیروی مغناطیسی
قانون نیروی لورنتس بیانگر رابطه بین میدان مغناطیسی با نیرویی است که توسط بار متحرک یا جریان احساس میشود. این قانون به صورت زیر بیان میشود:
اگر بار q با سرعت v در میدان مغناطیسی B حرکت کند، اندازه نیروی وارد شده بر آن از سمت میدان مغناطیسی برابر است با:
در رابطه فوق، زاویه بین سرعت ذره باردار و میدان مغناطیسی است. اگر ذره در راستای عمود بر میدان حرکت کند، نیروی وارد شده بر آن بیشینه خواهد بود. همچنین، اگر راستای حرکت ذره موازی B باشد، هیچ نیرویی بر آن وارد نخواهد شد.
رابطه بالا در مورد سیم قرار گرفته در میدان B و به طول L که از آن جریان I میگذرد نیز صدق خواهد کرد:
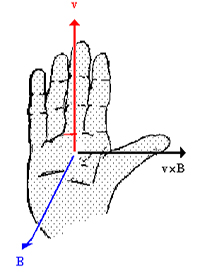
نکته: جهت نیروی لورنتس با استفاده از قانون دست راست تعیین میشود. اگر انگشت اشاره دست راست را در جهت حرکت بار مثبت و انگشت میانی را در جهت میدان مغناطیسی قرار دهید، انگشت شصت جهت نیرو را نشان خواهد داد (برای بار منفی جهت برعکس میشود).
مثال اول فرمول نیرو برای نیروی مغناطیسی
ذرهای با بار , با سرعت عمود بر میدان مغناطیسی به بزرگی ۰/۰۵ تسلا در حال حرکت است. اندازه نیروی وارد بر ذره را به دست آورید.
پاسخ
نیروی وارد بر ذرهای باردار که در میدان مغناطیسی حرکت میکند به صورت زیر به دست میآید:
رابطه فوق به صورت زیر نیز نوشته میشود:
در این مثال زاویه بین جهت حرکت بار الکتریکی و میدان مغناطیسی برابر 90 درجه است. در نتیجه مقدار برابر یک خواهد بود.
مثال دوم فرمول نیرو برای نیروی مغناطیسی
سیمی به طول هشت سانتیمتر در میدان مغناطیسی به اندازه ۶ تسلا قرار گرفته و با خطوط موازی میدان زاویه ۳۶ درجه ساخته است. اگر از این سیم جریانی با اندازه دو آمپر عبور کند، نیروی وارد شده بر سیم از طرف میدان مغناطیسی را حساب کنید.
پاسخ
نیروی وارد شده بر سیم حامل جریان در میدان مغناطیسی به صورت زیر محاسبه میشود:
در رابطه فوق، F بر حسب نیوتن، جریان I بر حسب آمپر و میدان مغناطیسی B بر حسب تسلا بیان میشوند. از آنجایی که سیم بر خطوط میدان عمود نیست، بیشینه نیرو را حس نخواهد کرد. این سیم، sin(36^o) از نیروی بیشینه را حس میکند.
مثال سوم فرمول نیرو برای نیروی مغناطیسی
میدان مغناطیسی در صفحه xy بر پروتونی که با سرعت حرکت میکند اعمال میشود. نیروی وارد شده بر پروتون را به دست آورید.
پاسخ
با استفاده از رابطه جهت نیروی وارد شده بر پروتون و اندازه آن را به دست میآوریم:
بنابراین، جهت نیروی مغناطیسی در راستای منفی محور z است.
مثال چهارم فرمول نیرو برای نیروی مغناطیسی
پروتونی () تحت تاثیر میدان مغناطیسی، داخل صفحه در مسیر دایرهای به دور محور ثابتی میچرخد. میدان مغناطیسی عمود بر صفحه و جهت آن به سمت داخل صفحه است. اگر شعاع حرکت دایره برابر ۹ سانتیمتر و سرعت حرکت پروتون برابر ۱/۶ کیلومتر بر ثانیه باشد، مقدار میدان مغناطیسی را به دست آورید.
پاسخ
ذره به هنگام حرکت در مسیر دایرهای، نیروی مرکزگرا را تجربه میکند. در این حالت، این نیرو توسط میدان مغناطیسی بر ذره وارد میشود. با استفاده از قانون دوم نیوتن در مورد حرکتهای دایرهای داریم:
در رابطه فوق بردار یکهای در راستای شعاع دایره و به سمت مرکز آن است. از آنجایی که نیروی مغناطیسی به سمت مرکز و زاویه بین میدان مغناطیسی و جهت حرکت پروتون برابر ۹۰ درجه است، داریم:
مثال پنجم فرمول نیرو برای نیروی مغناطیسی
بر روی سطح تپاختر یا ستاره پروتونی، اندازه میدان مغناطیسی بسیار قوی و در حدود تسلا است. الکترونی در اتم هیدروژن را بر روی سطح این ستاره در نظر بگیرید. فاصله متوسط بین الکترون و پروتون در حدود و سرعت متوسط الکترون برابر متر بر ثانیه است. بزرگی نیروی الکتریکی وارد شده بر الکترون که ناشی از میدان الکتریکی پروتون است را با بیشینه نیروی مغناطیسی وارد شده بر الکترون از طرف میدان مغناطیسی ستاره نوترونی مقایسه کنید. آیا انتظار دارید اتم هیدروژن تحت تاثیر میدان مغناطیسی در سطح ستاره نوترونی به طور کامل تغییر شکل دهد؟
پاسخ
فرضیههای مثال به صورت زیر است:
- الکترون در اتم هیدروژن در فاصله از پروتون قرار گرفته است.
- نیروی الکتریکی وارد شده بر الکترون با استفاده از رابطه به دست میآید.
- بیشینه نیروی مغناطیسی وارد شده بر الکترونی که با سرعت v در میدان B حرکت می کند با استفاده از رابطه محاسبه میشود.
با جایگزینی دادههای مثال در رابطه مربوط به نیروی الکتریکی داریم:
برای نیروی مغناطیسی داریم:
بیشینه نیروی مغناطیسی وارد شده بر الکترون در حدود 1000 برابر قویتر از نیروی الکتریکی وارد شده بر آن است. در نتیجه، انتظار داریم که اتم هیدروژن بر روی سطح ستاره نوترونی تغییر شکل دهد یا از بین برود.
تاکنون با فرمول نیرو برای نیروهای الکتریکی، مغناطیسی و وزن آشنا شدیم. در ادامه فرمول نیرو را برای نیروهای گریز از مرکز، نیروی شناوری و نیروی محرکه القایی بیان میکنیم.
فرمول نیروی گریز از مرکز و مرکز گرا چیست ؟
جسمی به جرم m را در نظر بگیرید که با سرعت v در مسیر دایرهای به شعاع r حرکت میکند. نیروی گریز از مرکز وارد شده بر این جسم با حاصلضرب جرم در مجذور سرعت حرکت آن رابطه مستقیم و با شعاع دایره نسبت عکس دارد. در ادامه، نیروی گریز از مرکز را تعریف و فرمول ریاضی آن را بیان میکنیم.
تعریف نیروی گریز از مرکز
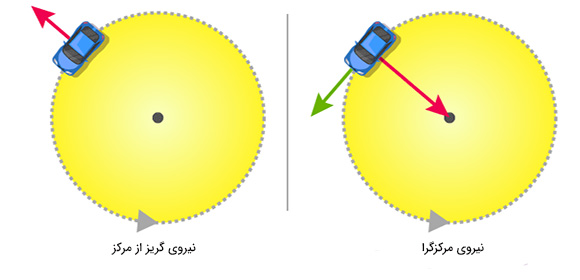
نیروی گریز از مرکز نیروی مجازی یا ساختگی به سمت بیرون است که توسط ذرهای در حال حرکت بر روی مسیر دایرهای حس میشود.
- جهت این نیرو به سمت خارج محور چرخش و موازی با آن است.
- نیروی گریز از مرکز از لحاظ بعد و اندازه با نیروی مرکزگرا برابر است. اما جهت نیروی مرکزگرا به سمت مرکز مسیر دایرهای است.
- عبارت ساختگی یا مجازی برای این نیرو استفاده میشود. زیرا این نیرو تنها زمانی حس خواهد شد که نیروی مرکزگرا وجود داشته باشد.
- این نیرو وابسته به جرم جسم، فاصله آن از مرکز و سرعت چرخش جسم است.
- از نیروی گریز از مرکز در بسیاری از وسایل چرخشی مانند جادههای ساحلی و سانتریفیوژهای چرخان استفاده میشود.
- یکای این نیرو، نیوتن است.
فرمول ریاضی نیروی گریز از مرکز و مرکز گرا
فرمول نیرو برای نیروی گریز از مرکز به صورت زیر نوشته میشود:
در رابطه فوق، v سرعت جسم متحرک، r فاصله جسم متحرک از مرکز و m جرم آن است.
اگر سرعت زاویهای جسم متحرک مشخص باشد، نیروی گریز از مرکز از رابطه زیر به دست خواهد آمد:
در رابطه فوق سرعت زاویهای، r فاصله جسم متحرک از مرکز و m جرم آن است.
نیروی گریز از مرکز چگونه محاسبه میشود ؟
فرض کنید سنگی به انتهای طنابی بسته شده است و شخصی آن را به دور سر خود میچرخاند. به منظور محاسبه نیروی گریز از مرکزی که سنگ حس میکند، گامهای زیر را طی میکنیم:
- جرم سنگ را تعیین میکنیم. فرض کنید سنگ 5 کیلوگرم است.
- طول نخ را به دست میآوریم. فرض کنید طول آن 10 متر باشد.
- سرعت حرکت سنگ را مشخص میکنیم. فرض میکنیم سرعت مماسی برابر ۵ متر بر ثانیه است. ذکر این نکته مهم است که سرعت مماسی (v) یا زاویهای () است. سرعت مماسی به صورت به دست میآید.
- نیروی گریز از مرکز را با استفاده از رابطه گفته شده در بالا به دست میآوریم.
مثال اول محاسبه نیروی گریز از مرکز یا نیروی مرکز گرا
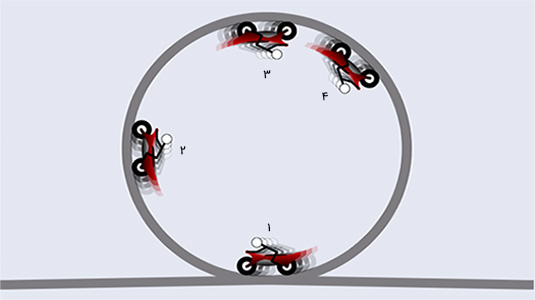
موتورسیکلتی به جرم 250 کیلوگرم با سرعت ثابت 11 متر بر ثانیه در مسیر دایرهای به قطر 12 متر حرکت میکند.
(الف) نیروهای عمودی و اصطکاک را در چهار حالت زیر به دست آورید.
- در پایینترین قسمت مسیر دایرهای و در حال بالا رفتن.
- پس از طی نصف مسیر به سمت بالا.
- در بالاترین نقطه.
- هنگامی که از بالاترین نقطه به اندازه زاویه ۴۵ درجه به سمت پایین حرکت کرد.
(ب) کمینه ضریب اصطکاک ایستایی به منظور اتمام این شیرینکاری را به دست آورید.
(جرم موتورسیکلت شامل جرم راننده و موتورسیکلیت است)
پاسخ
قسمت (الف): تنها نیروهای این مثال، نیروی وزن به سمت پایین، نیروی عمودی سطح به سمت مرکز مسیر دایرهای و نیروی اصطکاک مماس بر مسیر دایرهای هستند. وزن موتورسیکلت ثابت است. اندازه نیروی عمودی سطح از مقدار بیشینه در پایینترین نقطه مسیر دایرهای به مقدار کمینه در بالاترین نقطه این مسیر تغییر میکند. هنگامی که موتورسیکلت به سمت بالا حرکت میکند، نیروی وزن در خلاف جهت حرکت آن و به سمت پایین وارد میشودو بنابراین، نیروی اصطکاک در راستای حرکت موتورسوار بر آن اعمال میشود.
اما هنگامی که موتورسیکلت به سمت پایین حرکت میکند، نیروی وزن سعی در افزایش سرعت حرکت آن دارد. از این رو، نیروی اصطکاک در خلاف جهت حرکت بر آن وارد خواهد شد. موتورسوار سرعت خود را زیاد یا کم نمیکند، بلکه جهت آن را تغییر میدهد. این بدان معنا است که نیروی خالص همواره به سمت مرکز مسیر دایرهای است.
قسمت ۱: در این حالت، نیروی وزن به سمت پایین و نیروی عمودی سطح به سمت بالا است. جهت نیروی عمودی به سمت مرکز حرکت دایرهای . مقدار آن مثبت است. نیروی خالص کل، نیروی مرکزاگرا است و به صورت زیر نوشته میشود:
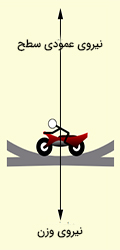
در این حالت به نیروی اصطکاک نیازی نیست، زیرا موتورسیکلت در مسیر افقی شتابی ندارد:
قسمت ۲: نیروی عمودی سطح در راستای افقی و به سمت مرکز قرار گرفته است. این نیرو با هیچ نیروی دیگری خنثی نمیشود. بنابراین، این نیرو، نیروی خالص افقی و نیروی مرکزگرا است:
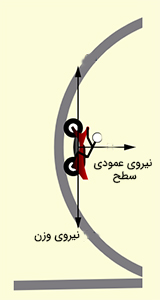
نیروی عمودی با نیروی وزن خنثی نمیشود، زیرا در خلاف جهت یکدیگر نیستند. موتورسیکلت هنگام حرکت به سمت بالا شتابی ندارد و با سرعت ثابت حرکت میکند. بنابراین، نیروی وزن باید با نیروی دیگری خنثی شود. این نیرو، نیروی اصطکاک است.
قسمت ۳: هر دو نیروی وزن و عمودی سطح به سمت پایین هستند.
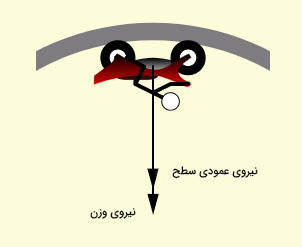
بنابراین نیروی خالص برابر جمع این دو نیرو است و به صورت زیر نوشته میشود:
مانند قسمت ۱، نیروی اصطکاک برابر صفر است، زیرا موتورسیکلت در راستای افق با سرعت ثابت حرکت میکند و شتابی ندارد.
قسمت ۴: نیروی عمودی سطح و نیروی اصطکاک بر یکدیگر عمود هستند. جهت نیروی عمودی سطح به سمت مرکز قرار گرفته است، بنابراین یکی از نیروهای مشارکت کننده در نیروی مرکزگرا است. نیروی اصطکاک بر مسیر حرکت مماس است و هیچ دخالتی در نیروی مرکزگرا ندارد. بردار وزن باید به مولفههای خود تجزیه شود. مولفهای که در راستای مرکز است، در نیروی مرکزگرا مشارکت دارد.
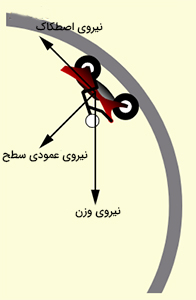
برای نیروی عمودی سطح داریم:
همچنین، مولفه نیروی وزن که مماس بر مسیر حرکت است، با نیروی اصطکاک خنثی میشود (سرعت حرکت ثابت است).
برای این مثال، راه حل سادهتری نیز وجود دارد. چه نیروهایی در این مثال ثابت هستند؟ وزن و نیروی مرکزگرا. چه چیزی تغییر میکند؟ جهت حرکت. نیروهای وزن و مرکزگرا را به دست میآوریم.
برای نیروی وزن داریم:
همچنین برای نیروی گریز از مرکز داریم:
در قسمت ۱ نیروی وزن به سمت پایین و نیروی عمودی سطح به سمت بالا قرار گرفتهاند. تفاوت این دو نیرو (نیروی خالص) برابر نیروی مرکزگرا است. بنابراین داریم:
از آنجایی که حرکت در راستای افقی با سرعت ثابت است، نیروی اصطکاک برابر صفر است.
در قسمت ۲، نیروی عمودی به سمت مرکز قرار گرفته است. در نتیجه، این نیرو، نیروی مرکزگرا است.
نیروی اصطکاک با نیروی وزن خنثی میشود. در این صورت موتورسیکلت به حرکت خود با سرعت ثابت ادامه خواهد داد.
در قسمت ۳، نیروهای وزن و عمودی به سمت پایین و به طرف مرکز قرار گرفتهاند. جمع آنها برابر نیروی مرکزگرا است.
مانند قسمت ۲، نیروی اصطکاک برابر صفر است.
در قسمت ۴، زوایه ۴۵ درجه است و مقدارهای سینوس و کسینوس آن با هم برابر هستند. در نتیجه به محاسبات کمتری نیاز است.
جهت نیروهای عمودی سطح و مولفه نیروی وزن به سمت مرکز است. بنابراین، جمع آنها برابر نیروی مرکزگرا است:
مولفه دیگر وزن برابر (مولفه موازی دایره) با نیروی اصطکاک خنثی میشود. در نتیجه، نیروی خالص مماسی برابر صفر است (حرکت با سرعت ثابت است).
قسمت (ب): نیروی اصطکاک ایستایی هنگامی که موتورسیکلت در حالت عمودی قرار دارد، بیشترین مقدار را دارد. نیروی اصطکاک بین لاستیک و کف باید با نیروی وزن خنثی شود. در این صورت، شتاب مماسی بر مسیر دایرهای برابر صفر خواهد بود.
در دو نقطه، نیروی اصطکاک برابر نیروی وزن و نیروی عمودی سطح برابر نیروی مرکزگرا است.
- هنگامی که موتورسوار به سمت پایین حرکت میکند.
- هنگامی که موتورسوار به سمت بالا میرود.
این قسمت را نیز با استفاده از دو روش حل میکنیم.
در روش اول داریم:
در روش دوم داریم:
فرمول نیروی شناوری چیست ؟
به زبان ساده، نیروی شناوری متناسب با چگالی مایع، شتاب جاذبه زمین یا g و حجم مایع جابجا شده است. اما سوالی که ممکن است مطرح شود آن است که نیروی شناوری چیست؟ در ادامه، تعریف سادهای از این نیرو ارائه میشود و رابطه ریاضی آن با حل مثالهای گوناگون توضیح داده میشود.
نیروی شناوری چیست ؟
آیا تاکنون عینک شنا را در عمیقترین قسمت استخر انداختهاید و برای برداشتن آن شنا کردهاید؟ اگر این کار را انجام داده باشید، به طور حتم متوجه شدهاید که کار بسیار سختی است. زیرا هنگامی که در تلاش برای شنا کردن به سمت پایین هستنید، نیرویی از سمت آب شما را به سمت بالا و سطح هل میدهد. به این نیروی رو به بالا که بر اجسام غوطهور در مایعات وارد میشود، نیروی شناوری گفته میشود.

رابطه ریاضی فرمول نیروی شناوری چیست ؟
نیروی شناوری با استفاده از فرمول زیر به دست میآید:
با استفاده از رابطه بالا میتوان نیروی شناوری وارد شده بر هر جسمی را که به طور کامل یا جزیی در مایعی غوطهور شده باشد به دست آورد. در این رابطه چگالی مایعی است که جسم در آن قرار گرفته است. g شتاب جاذبه زمین و حجم مایع جابجا شده است.
خوشبختانه، نیروی شناوری به عمق کلی که جسم در مایع غوطهور شده است بستگی ندارد. به بیان دیگر، تا هنگامی که جسمی به طور کامل در مایع غوطهور شده است، بردن آن به قسمت عمیقتر مایع، تغییری در اندازه نیروی شناوری ایجاد نخواهد کرد. شاید در نگاه اول، توضیح قبل درست به نظر نرسد. زیرا با افزایش عمق، مقدار فشار افزایش مییابد. اما توجه به این نکته مهم است که فشار در قسمت بالا و پایین جسم به اندازه یکسانی افزایش مییابند و یکدیگر را خنثی میکنند.
اصل ارشمیدس چیست ؟
فرمول نیرو برای نیروی شناوری را به صورت زیر مینویسیم:
اگر به رابطه بالا دقت کنید، به نتیجه جالبی خواهید رسید. عبارت برابر با چگالی مایع جابجا شده در حجم آن است. با توجه به تعریف چگالی به صورت ، جرم به صورت تعریف خواهد شد. در نتیجه، برابر جرم مایع جابجا شده خواهد بود. بنابراین، رابطه فوق به صورت زیر نوشته میشود:
به رابطه به دست آمده دقت کنید. حاصلضرب جرم مایع جابجا شده در شتاب جاذبه زمین برابر وزن مایع جابجا شده است. بنابراین، فرمول نیروی شناوری به صورت زیر نوشته خواهد شد:
این رابطه به اصل ارشمیدس معروف است. بر طبق اصل ارشمیدس، نیروی شناوری اعمال شده بر جسم برابر با وزن مایع جابجا شده توسط آن جسم است.
مثال اول فرمول نیروی شناوری
مجسمه کوچکی به وزن ۰/۶۵۰ کیلوگرم به داخل دریاچهای انداخته میشود و تا عمق ۳۵ متری دریاچه پایین میرود. این مجسمه جامد است (بدون هیچ حفرهای) و حجم کلی را اشغال کرده است. اگر چگالی آب دریاچه برابر باشد، مقدار نیروی شناوری وارد شده بر مجسمه را به دست آورید.
پاسخ
فرمول نیروی شناوری عبارت است از:
با جایگذاری دادههای مثال در رابطه بالا داریم:
مثال دوم فرمول نیروی شناوری
مکعبی به وزن ۲/۳۳ کیلوگرم را در نظر بگیرید. کمینه طول مکعب چقدر باید باشد تا در آب دریا با چگالی ، شناور بماند؟
پاسخ
اگر جسمی بخواهد بر روی آب شناور بماند باید نیروی شناوری با وزن آن برابر باشد.
با نوشتن فرمول نیرو برای وزن و نیروی شناوری داریم:
حجم مکعب برابر است، با قرار دادن آن در رابطه فوق، داریم:
مثال سوم فرمول نیروی شناوری
بالون کروی پر شده از هلیومی به وزن ۹/۲۰ کیلوگرم به شکل گاو طراحی و به کمک طنابی بر روی زمین بسته شده است. اگر قطر بالون برابر ۳/۵۰ متر و چگالی هوا برابر باشد، نیروی کشش طناب را به دست آورید.
پاسخ
در ابتدا نمودار جسم آزاد را برای بالون رسم میکنیم.
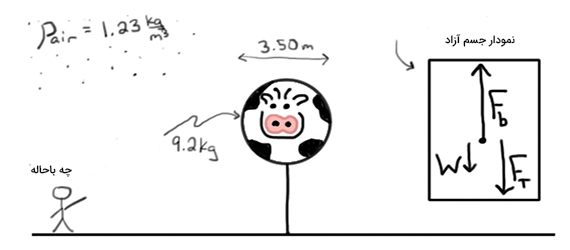
در این مثال، شاره مورد نظر هوا است. از آنجایی که بالون ساکن است، نیروهای وارد شده با یکدیگر در حالت تعادل قرار دارند. بنابراین، جمع نیروهای رو به بالا برابر با جمع نیروهای رو به پایین است.
با قرار دادن فرمول نیروی شناوری و وزن در رابطه بالا داریم:
نیروی کشش طناب برابر است با:
فرمول نیرو محرکه القایی چیست ؟
برای محاسبه نیرو محرکه القایی از دو فرمول استفاده میشود.
| فرمول نیرو محرکه القایی | تعریف پارامترهای مورد استفاده |
| = نیرو محرکه القایی
E = انرژی موجود در مدار Q = بار موجود در مدار | |
| I = جریان
= نیرو محرکه القایی R = مقاومت مدار r = مقاومت داخلی باتری |
فرمول نیروی مقاومت هوا چیست ؟
هنگامی که جسمی به سمت بالا پرتاب میشود، از طرف هوا بر آن نیرویی در خلاف جهت حرکت وارد میشود. نام این نیرو، نیروی مقاومت هوا است. در بیشتر مسائل فیزیک، این نیرو نادیده گرفته میشود.
اما به منظور داشتن درک بهتری از حرکت اجسام سریع مانند هواپیماها، در نظر گرفتن این نیرو بسیار حیاتی است. اندازه این نیرو به چگالی هوا، مساحت جسم در حرکت، سرعت حرکت آن و ضریب درگ بستگی دارد. ضریب درگ به دیگر مشخصات جسم مانند زبری سطح و آشوب آن بستگی دارد. به نیروی مقاومت هوا، نیروی درگ نیز میگویند و واحد اندازهگیری آن نیوتن است.
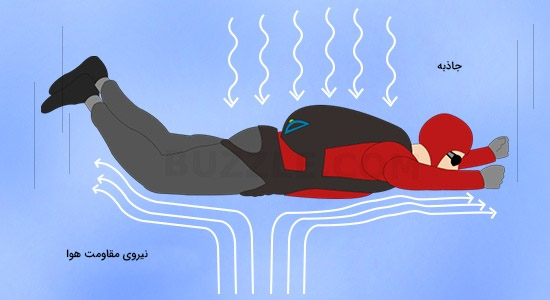
F = نیروی ناشی از مقاومت هوا
k = ضریب ثابتی که شامل چگالی، ضریب درگ و مساحت است.
v = سرعت حرکت جسم
= چگالی هوا
= ضریب درگ
A = مساحت تماس جسم با هوا
مثال اول فرمول نیروی مقاومت هوا
هواپیمایی با سرعت ۲۵۰/۰ متر بر ثانیه حرکت میکند. مساحت بالهای هواپیما که در معرض هوا است، برابر ۵۰۰ متر مربع است. اگر چگالی هوا در ارتفاعی که هواپیما پرواز میکند برابر باشد، نیروی مقاومت هوا را بر هواپیما به دست آورید. فرض کنید ضریب درگ برابر ۰/۰۲۴ است.
پاسخ
نیروی مقاومت هوا با استفاده از فرمول زیر به دست میآید:
با جایگذاری دادههای مثال، در رابطه بالا داریم:
مثال دوم فرمول نیروی مقاومت هوا
چتربازی پس از پرش از هواپیما، به سمت زمین با سرعت ثابت حرکت میکند. نیروی وارد شده به دلیل جاذبه برابر 500 نیوتن است. اگر چگالی هوا برابر ، مساحت چتر برابر ۷۵/۰ متر مربع و ضریب درگ برابر ۱/۷۵ باشد، سرعت حرکت چترباز چقدر خواهد بود؟
پاسخ
سرعت حرکت چترباز با استفاده از فرمول نیروی مقاومت هوا به صورت زیر به دست میآید:
طبق صورت مثال، چترباز با سرعت ثابت حرکت میکند. در نتیجه، نیروی وزن برابر نیروی مقاومت هوا خواهد بود. بنابراین، مقدار نیروی مقاومت هوا نیز برابر 500 نیوتن است.
فرمول نیروی عمودی سطح چیست ؟
هنگامی که جسمی بر روی سطح افقی قرار گرفته است، فرمول نیرو برای نیروی عمودی سطح برابر نیروی وزن است. اما اگر جسم بر روی سطح شیبدار یا سطوح مشابهی قرار داشته باشد، فرمول نیروی برای نیروی عمودی سطح متفاوت خواهد بود.
فرمول نیرو و سرعت
تاکنون با فرمول نیرو برای نیروهای مختلف آشنا شدید. اما سوالی که ممکن است مطرح شود آن است که رابطه نیرو با سرعت حرکت جسم چیست؟ در ادامه، این رابطه به اخنصار توضیح داده میشود.
نیرو به صورت تغییرات تکانه بر حسب زمان تعریف میشود:
تکانه برابر با حاصلضرب جرم در سرعت است. بنابراین، نیرو برابر تغییرات جرم در سرعت نسبت به زمان است:
در بیشتر موقعها جرم ثابت در نظر گرفته میشود. اما این فرض یک روند کلی نیست و گاهی سرعت ثابت است و جرم تغییر میکند. با فرض ثابت بودن جرم، نیرو به صورت زیر نوشته میشود:
اگر جسمی با سرعت ثابت حرکت کند، نیروی وارد شده بر آن برابر صفر خواهد بود.
گاهی مواقع، جرم و سرعت هر دو تغییر میکنند. به عنوان مثال، موشکی را در نظر بگیرید که در حال شتاب گرفتن سوخت از آن خارج می شود.
معرفی فیلم آموزش علوم تجربی پایه نهم - بخش فیزیک
مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش علوم تجربی پایه نهم - بخش فیزیک برای دانشآموزان پایه نهم کرده که این مجموعه آموزشی از چهار درس تشکیل شده است.
در درس یکم، حرکت و انواع آن آموزش داده شده است. در این درس، سرعت و شتاب لحظهای و متوسط را همراه با حل تمرین و انجام آزمایش فرا میگیرید. در این مطلب در مورد فرمول نیرو برای انواع نیروهای مختلف توضیح داده شد. بنابراین، تماشای درس دوم در مورد مبحث نیرو کمک شایانی به درک بهتر فرمول انواع نیروها خواهد کرد. در این درس، با انواع نیرو، نیروهای متوازن و نامتوازن، اثرات نیرو بر یک جسم، نیروی خالص موثر بر شتاب و نیروهای کنش و واکنش آشنا میشوید. در نتیجه، پس از خواندن این مطلب و تماشای درس دوم به درک بهتری از فرمول نیرو برای نیروهای مختلف خواهید رسید.
فشار گازها، مایعات و جامدات در درس سوم توضیح داده میشود. در درس چهارم این مجموعه ماشین و انواع آن را فرا خواهید گرفت.
- برای دیدن فیلم آموزش علوم تجربی پایه نهم - بخش فیزیک + اینجا کلیک کنید.
معرفی فیلم آموزش فیزیک عمومی ۲ - حل مساله
مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک عمومی ۲ - بحل مساله برای دانشجویان رشتههای فنی و مهندسی و فیزیک کرده که این مجموعه آموزشی از هفت درس تشکیل شده است.
در درس یکم میدان و پتانسیل الکتریکی آموزش داده میشود. در این مطلب با فرمول نیرو برای نیروی الکتریکی و قانون کولن آشنا شدید. پس از تماشای درس اول این مجموعه آموزشی درک بهتری از نیروی الکتریکی وارد شده بر اجسام مختلف باردار در میدان الکتریکی خارجی خواهید داشت. همچنین، فرمول نیروی مغناطیسی را در درس پنجم یاد خواهید گرفت. در این درس، نیروی مغناطیسی وارد بر بار نقطهای، نیروی مغناطیسی وارد بر هادی حامل جریان و نیروی وارد بر حلقه حامل جریان در میدان مغناطیسی محاسبه شده است. در نتیجه، خواندن این مطلب در کنار تماشای این مجموعه آموزشی به شما درک بهتری از فرمول نیرو برای نیروهای الکتریکی و مغناطیسی خواهد داد.
- برای دیدن فیلم آموزش فیزیک عمومی ۲ - حل مساله + اینجا کلیک کنید.
جمعبندی
در این مطلب از مجله فرادرس با فرمول نیرو برای انواع نیروهای مختلف همراه با حل مثالهای گوناکون آشنا شدید. در حالت کلی، نیرو به صورت حاصلضرب جرم جسم بر حسب کیلوگرم در سرعت حرکت جسم بر حسب متر تعریف میشود.
آزمون فرمول نیرو
۱. فرمول اصلی نیرو طبق قانون دوم نیوتن و متغیرهای آن چیست؟
نیرو تفاوت شتاب (a) و سرعت اولیه جسم است.
نیرو برابر است با حاصل ضرب جرم (m) در شتاب (a) جسم.
نیرو جمع مساحت سطح و چگالی جسم است.
نیرو حاصل جمع جرم (m) و شتاب (a) است.
طبق قانون دوم نیوتن، نیرو با ضرب کردن مقدار جرم (m) در شتاب (a) جسم به دست میآید.
۲. در سیستم SI، واحد استاندارد نیرو چیست و چگونه با دیگر یکاهای فیزیکی مرتبط میشود؟
ژول (Joule) است و بر پایه کیلوگرم در متر بر ثانیه تعریف میشود.
نیوتون (Newton) است و برابر با حاصل ضرب کیلوگرم در متر بر مجذور ثانیه است.
پاسکال (Pascal) است و به نسبت جرم به شتاب بستگی دارد.
وات (Watt) است و معادل نیوتون ضربدر متر است.
نیرو در سیستم SI با واحد نیوتون (Newton) سنجیده میشود. طبق قانون دوم نیوتن، یک نیوتون مقدار نیرویی است که به جسمی با جرم یک کیلوگرم شتاب یک متر بر مجذور ثانیه بدهد. بنابراین، نیوتون با حاصل ضرب کیلوگرم (kg) در متر بر مجذور ثانیه (m/s²) مرتبط است.
۳. کدام ویژگی نیرو باعث میشود جهت آن در حل مسائل اهمیت ویژهای داشته باشد؟
نیرو یک کمیت برداری است و جهت مشخص دارد.
نیرو مستقل از مسیر اثر خود عمل میکند.
جهت نیرو همواره ثابت میماند و تغییر نمیکند.
نیرو فقط بزرگی دارد و جهت ندارد.
خاصیت برداری بودن نیرو به این معناست که نیرو هم اندازه و هم جهت دارد و جهت آن در تعیین نتیجه حرکت یا وضعیت جسم نقش اساسی ایفا میکند. به همین دلیل در حل مسائل، جهت نیرو باید به دقت در نظر گرفته شود.
۴. کدام عبارت به درستی تفاوت جرم و وزن را در فیزیک بیان میکند؟
جرم مقدار نیروی وارد شده به جسم است اما وزن مقدار ماده جسم را نشان میدهد.
جرم و وزن همواره مقدار عددی برابری دارند.
جرم و وزن هر دو فقط در حضور گرانش تغییر میکنند.
جرم مقدار ماده جسم است و وزن نیروی جاذبه زمین بر جسم است.
در فیزیک جرم (mass) تعریفی مستقل از نیرو دارد و نشاندهنده میزان ماده موجود در جسم است، در حالی که وزن (weight) نیرویی است که بر اثر کشش جاذبه زمین بر جرم آن وارد میشود.
۵. وقتی چند نیرو به طور همزمان به یک جسم وارد شود، منظور از برآیند برداری نیروها چیست و باید به کدام ویژگی توجه کرد؟
حاصلجمع نیروها با توجه به جهت هریک برای پیدا کردن نیروی کل
نیروی بیشینه هر نیرو به طور جداگانه معیار اصلی محاسبه است.
نیروی حاصل جمع جبری همه نیروهای واردشده است، بدون در نظر گرفتن جهت آنها.
نیروها همیشه برهم منطبق هستند و جمع آنها تفاوتی ایجاد نمیکند.
برآیند برداری نیروها یعنی برای محاسبه نیروی کل باید هم مقدار و هم جهت هر نیرو را در نظر گرفت، زیرا نیرو یک کمیت برداری است و فقط جمع کردن مقادیر بدون توجه به جهت ممکن است نتیجه نادرست بدهد. عبارت «حاصلجمع نیروها با توجه به جهت هریک» دقیق است زیرا نیروهایی که همجهت باشند تقویت و نیروهای خلاف جهت از هم کم میشوند.
۶. نیروی وزن یک جسم چگونه محاسبه میشود و شتاب جاذبه چه نقشی در این فرمول دارد؟
وزن برابر با شتاب جسم تقسیم بر جرم است.
وزن مجموع جرم و شتاب جاذبه است.
وزن حاصلضرب جرم در شتاب جاذبه است.
وزن فقط به جرم جسم بستگی دارد و به شتاب جاذبه بستگی ندارد.
وزن یک جسم توسط رابطه حاصلضرب جرم در شتاب جاذبه به دست میآید، یعنی اگر جرم جسم مشخص باشد و مقدار شتاب جاذبه (g) نیز معلوم باشد، وزن را میتوان مستقیما محاسبه کرد.
۷. برای محاسبه نیروی اصطکاک جنبشی طبق اصول بیانشده، به کدام عوامل و فرمول نیاز است؟
نیروی عمودی سطح و ضریب اصطکاک جنبشی در فرمول Fk = μk × N
جرم جسم و شتاب گرانشی در فرمول F = m × g
سرعت و چگالی هوا طبق فرمول مقاومت هوا
بار الکتریکی و فاصله طبق فرمول کولن
نیروی اصطکاک جنبشی با استفاده از نیروی عمودی سطح و ضریب اصطکاک جنبشی به دست میآید و فرمول آن Fk = μk × N است. این رابطه دقیقا اشاره به نقشی دارد که جنس سطح و شدت تماس (نیروی عمودی) در مقدار اصطکاک دارند. استفاده از جرم و شتاب گرانشی، صرفا وزن را مشخص میکند. بار الکتریکی و فاصله به نیروی الکتریکی مرتبط است و سرعت و چگالی هوا نیز تنها در نیروی مقاومت هوا اهمیت دارند.
۸. از نظر فیزیکی، تفاوت اصلی اصطکاک ایستایی و اصطکاک جنبشی چیست و هر کدام در چه شرایطی به کار میروند؟
اصطکاک ایستایی قبل از حرکت جسم عمل میکند و بزرگتر از اصطکاک جنبشی است. اصطکاک جنبشی هنگام حرکت جسم فعال است.
اصطکاک ایستایی در سطح زبر وجود ندارد و اصطکاک جنبشی فقط در سطوح صاف عمل میکند.
اصطکاک ایستایی مربوط به سیالات است ولی اصطکاک جنبشی در جامدات رخ میدهد.
اصطکاک ایستایی تنها برای اجسام سبک به کار میرود. اصطکاک جنبشی برای اجسام سنگین استفاده میشود.
اصطکاک ایستایی زمانی ظاهر میشود که جسم هنوز شروع به حرکت نکرده و نیروی لازم برای غلبه بر آن معمولا بیشتر از اصطکاک جنبشی است. هنگامی که جسم شروع به حرکت کند، اصطکاک جنبشی وارد عمل میشود و مقدارش نسبت به حالت ایستایی کمتر است.
۹. کدام عاملها به طور مستقیم بیشترین تاثیر را بر مقدار نیروی اصطکاک دارند؟
فقط جرم جسم مقدار نیروی اصطکاک را تعیین میکند و عوامل دیگر بی تاثیرند.
نیروی اصطکاک مستقل از نیروی عمودی سطح و فقط وابسته به نوع سطوح است.
افزایش سرعت جسم همواره باعث افزایش نیروی اصطکاک میشود حتی اگر سایر عوامل ثابت بمانند.
هرچه ضریب اصطکاک و نیروی عمودی سطح بیشتر شوند، نیروی اصطکاک نیز بیشتر میشود.
نیروی اصطکاک به صورت حاصلضرب ضریب اصطکاک و نیروی عمودی سطح به دست میآید، بنابراین هر دو عامل یعنی «ضریب اصطکاک» و «نیروی عمودی سطح» افزایش یابند، مقدار نیروی اصطکاک نیز افزایش خواهد یافت.
۱۰. طبق قانون کولن، کدام حالت باعث بیشترین نیروی الکتریکی میان دو بار میشود؟
بارها زیاد باشند اما فاصله بسیار زیاد باشد.
بارها بیشترین مقدار را داشته باشند و فاصله کم باشد.
بارها کوچک باشند و فاصله زیاد باشد.
بارها اندازه متوسط داشته باشند و فاصله کم باشد.
بیشترین نیروی الکتریکی طبق قانون کولن زمانی رخ میدهد که مقدار هر دو بار زیاد باشد و فاصله میان آنها کم باشد. نیروی الکتریکی با مقدار بارها نسبت مستقیم و با فاصله نسبت معکوس مجذور دارد. پس اگر «بارها بیشترین مقدار را داشته باشند و فاصله کم باشد»، حاصلضرب بارها زیاد و مخرج کسر کوچک میشود و نیروی بیشینه به دست میآید.
۱۱. بر اساس قانون کولن، اگر فاصله بین دو بار الکتریکی افزایش یابد، مقدار نیروی بین آنها چگونه تغییر میکند؟
نیروی بین دو بار تغییر نمیکند مگر بارها یکسان باشند.
نیروی بین دو بار ثابت میماند.
نیروی بین دو بار افزایش مییابد.
نیروی بین دو بار کاهش مییابد.
طبق قانون کولن، نیروی الکتریکی میان دو بار، رابطه معکوس با مجذور فاصله دارد. به این معنا که اگر فاصله زیاد شود، مقدار نیرو کاهش مییابد. فاصله همیشه بر نیرو اثرگذار است و بارها چه برابر چه متفاوت باشند این رابطه برقرار است.
۱۲. اگر نیروی وارد بر جسم و شتاب آن را داشته باشیم، چگونه میتوان جرم جسم را به دست آورد؟
شتاب را از نیرو کم میکنیم.
جرم را بر نیرو ضرب میکنیم.
نیرو و شتاب را با هم جمع میکنیم.
نیرو را بر شتاب تقسیم میکنیم.
برای پیدا کردن جرم وقتی نیرو و شتاب داده شده باشد، باید مقدار نیرو را بر مقدار شتاب تقسیم کنیم. فرمول اصلی نیرو برابر است با جرم ضربدر شتاب (F = m × a) و اگر جرم مجهول باشد، از همین رابطه نتیجه میگیریم که جرم برابر است با «نیرو بر شتاب».
۱۳. وقتی موتورسیکلتی با سرعت ثابت v در مسیر دایرهای حرکت میکند، کدام نیرو باعث ماندن آن روی مسیر است و این نیرو چه رابطهای با جرم و شعاع حرکت دارد؟
نیروی وزن. برابر با حاصلضرب جرم و شتاب جاذبه
نیروی اصطکاک جنبشی. متناسب با جرم و سرعت
نیروی مرکزگرا. برابر با حاصلضرب جرم، مربع سرعت و معکوس شعاع
نیروی گریز از مرکز. متناسب با جرم و شعاع حرکت
در حرکت دایرهای، نیروی مرکزگرا همان نیرویی است که جسم را به سمت مرکز دایره نگه میدارد. طبق فرمول مطرح شده، مقدار این نیرو برابر است با جرم ضربدر مربع سرعت، تقسیم بر شعاع مسیر. عبارت دقیقا برابر با است. نیروی گریز از مرکز واقعی نبوده و از دیدگاه چارچوب غیرلخت مطرح میشود، و نقشی در نگه داشتن جسم روی مسیر ندارد.
۱۴. فرمول نیروی عمودی سطح برای جسمی روی سطح شیبدار بدون اصطکاک با زاویه θ و جرم m چیست؟
N = m × g × tanθ
N = m × g × cosθ
N = m × g / cosθ
N = m × g × sinθ
فرمول صحیح برای نیروی عمودی سطح در شرایط بدون اصطکاک برابر با "N = m × g × cosθ" است، زیرا نیروی عمودی برابر مولفه وزن عمود بر سطح است.
۱۵. طبق اصل ارشمیدس، نیروی شناوری وارد بر یک جسم غوطهور چگونه به چگالی مایع و حجم جابجا شده وابسته است؟
نیروی شناوری فقط به جرم جسم وابسته است و ربطی به چگالی مایع ندارد.
نیروی شناوری تنها وابسته به حجم جسم و شتاب جاذبه است و چگالی تاثیر ندارد.
نیروی شناوری برابر است با حاصلضرب چگالی مایع، حجم جابجا شده و شتاب گرانشی.
نیروی شناوری تنها به چگالی جسم نسبت به هوا وابسته است.
بر اساس اصل ارشمیدس، نیروی شناوری معادل با وزن مایع جابجا شده توسط جسم است، یعنی حاصلضرب چگالی مایع، حجم جابجا شده و شتاب گرانشی.
۱۶. در بررسی وضعیت جسمی که چند نیرو با جهتهای مختلف دریافت میکند، کدام روش برای تشخیص تعادل یا عدم تعادل کل سیستم صحیح است؟
جمع نیروها به صورت برداری و بررسی صفر شدن نیروی کلی
استفاده از فرمول جرم ضربدر شتاب برای هر نیرو به تنهایی
مقایسه اندازه بزرگترین نیرو با مجموع نیروهای دیگر
جمع کردن عددی همه نیروها بدون توجه به جهت
زمانی که چند نیرو بر جسمی اثر میگذارند، فقط با جمع برداری همه نیروها میتوان وضعیت کل سیستم را تعیین کرد. اگر جمع برداری نیروها برابر صفر باشد، سیستم در حالت تعادل است.
۱۷. وقتی جرم و سرعت یک موشک همزمان تغییر میکند، چگونه رابطه بین نیرو و تکانه برقرار است و تحلیل درست کدام است؟
نیرو برابر با حاصلضرب جرم ثابت در تغییر شتاب است.
نیرو فقط برابر با جرم ضربدر شتاب است و تغییر جرم اثری ندارد.
در این حالت نیرو ثابت باقی میماند و تغییری نمیکند.
نیرو برابر با تغییر تکانه نسبت به زمان است حتی اگر جرم تغییر کند.
وقتی جرم و سرعت موشک هر دو تغییر میکنند، نیرو با مشتق تکانه نسبت به زمان تعریف میشود. این یعنی تغییر ترکیبی جرم و سرعت بر نیروی وارد اثر میگذارد و باید از مفهوم مشتق تکانه برای بیان نیرو استفاده کرد. فرمول معمول نیرو=جرم×شتاب فقط برای جرم ثابت صدق میکند.













سلام مطلب بسيار اموزنده بود من را ياد دوران تحصيل انداخت در اون روزگار دبيران محترم چقدر زحمت ميكشيدند تا اين مطالب را به دانش اموزان تفهيم كنند ولى مطالب فوق اينقدر زيبا وراحت بيان شده كه كاقيه فقط دانش اموز يكبار اين مطلب را با دقت مطالعه كنه
خیلی کامل و عالی 🙌
دم شما گرم 🌹