داده دو وضعیتی و تحلیل پانلی | پیاده سازی GEE در SPSS

پدیده‌های بسیاری در دنیای واقعی وجود دارند که با قالب داده‌های پانلی مطابقت دارند. در حقیقت سری‌های زمانی چند متغیره را می‌توان به نوعی داده پانلی تصور کرد. حال در نظر بگیرید که داده دو وضعیتی و تحلیل پانلی را بخواهیم در محیط SPSS مورد بررسی قرار داده و مدلی را بر مبنای تکنیک ناپارامتری «معادلات برآوردیابی تعمیم یافته» (Generalize Estimating Equations) یا GEE ایجاد کنیم. در این نوشتار، به این موضوع پرداخته و کدهای مربوط به داده دو وضعیتی و تحلیل پانلی را در محیط Syntax نرم افزار SPSS توضیح خواهیم داد.

در نوشتارهای دیگر از مجله فرادرس موضوع داده پانلی و همچنین روش یا تکنیک GEE مورد بحث قرار گرفته است. بنابراین اگر درباره این دو موضوع، احتیاج به اطلاعاتی بیشتری دارید، بهتر است قبل از مطالعه این مطلب، با خواندن معادلات برآوردیابی تعمیم یافته (GEE) در آمار | به زبان ساده و داده‌ پانلی (Panel Data) — از صفر تا صد برخی اصطلاحات رایج در این حوزه را بشناسید. همچنین خواندن نوشتارهای آزمون هاسمن برای داده‌ پانلی (Hausman Test) — به زبان ساده و تحلیل داده پانلی در SPSS — راهنمای کاربردی نیز خالی از لطف نیست.

داده دو وضعیتی و تحلیل پانلی

معمولا متغیرهای پاسخ برای مدل‌بندی داده‌های پانلی، مقادیر کمی و از نوع پیوسته هستند. البته متغیرهای پاسخ با مقادیر دو دویی یا «دو وضعیتی» (Binary Response Variables)، در تحلیل داده پانلی نیز می‌توانند به کار گرفته شوند. کافی است که توزیع مورد نظر برای متغیرهای موجود در مدل را با «توزیع دو جمله‌ای» (Binomial Distribution) یکسان در نظر بگیرید. در ادامه این مطلب، از یک مثال واقعی براساس داده‌های «افسردگی بعد از زایمان» (Postnatal Depression) استفاده کرده و نحوه مدل‌سازی و برآورد پارامترها را به کمک تکنیک GEE در محیط SPSS، اجرا خواهیم کرد.

فیلم آموزش تحلیل رگرسیون لجستیک دو حالتی در SPSS اس پی اس اس در فرادرس

کلیک کنید

فرض کنید که برای یک نمونه از بیماران دارای افسردگی پس از زایمان، شاخص یا «مقیاس افسردگی پس از زایمان ادینبورگ» (EPDS یا Edinburgh Postnatal Depression Scale) اندازه‌گیری شده است. این اطلاعات در فایل depressed01.sav ذخیره و در دسترس شما قرار دارند. به منظور دریافت این فایل با قالب فشرده (zip)، کافی است، اینجا کلیک کنید. مشخص است که پس از خارج کردن این فایل از حالت فشرده، می‌توانید آن را در نرم‌افزار SPSS‌ فراخوانی کنید. البته با فرض اینکه محل فایل در درایو D‌ باشد، از کد زیر نیز می‌توانید کمک بگیرید.

1get file = 'D:depressed01.sav'.

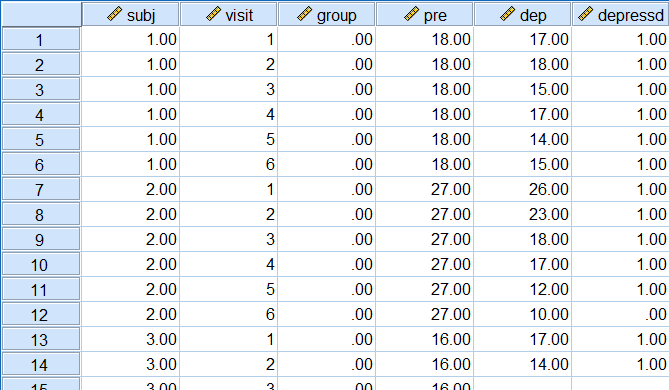
ابتدا بهتر است به ساختار این مجموعه داده نگاهی بیاندازیم. در تصویر ۱، نمونه‌ه‌ای از این داده‌ها را در برگه Data View نرم‌افزار SPSS، مشاهده می‌کنید.

متغیر subj نشانگر کد یا شماره سریال بیمار است. ۶۱ بیمار مورد بررسی قرار گرفته و در دو گروه درمان به کمک دارونما (با کد group = 0) و گروه درمان با دارو (group = 1) تفکیک شده‌اند. متغیر visit نیز نشانگر ماه مورد نظر برای اندازه‌گیری در یک دوره شش ماهه است. از آنجایی که حداکثر مراجعات بیمار برای اندازه‌گیری، برابر با شش خواهد بود، مقادیر این متغیر، از ۱ تا ۶ تغییر می‌کنند.

همانطور که گفته شد، متغیر group تعیین می‌کند که آیا بیمار در گروه کنترل (دارونما) یا در گروه تیمار (درمان با دارو) قرار دارد. کد ۱ نشانگر گروه تیمار و کد صفر نشانگر گروه کنترل است.

همچنین، قبل از اجرای برنامه درمان، میزان افسردگی بیماران اندازه‌گیری شده و در متغیر pre ثبت شده است. میزان افسردگی در هر دوره نیز در متغیر dep مشخص شده.

در متغیری به نام depressed که یک متغیر دو وضعیتی است، تعیین شده که چه بیماری، در هر ماه از دوره شش ماهه درمان، میزان افسردگی بیشتر یا مساوی با ۱۱ دارد. بنابراین کد صفر نشانگر کمتر بودن میزان افسردگی از ۱۱ را نشان می‌دهد و کد ۱، نمایانگر بیشتر بودن میزان افسردگی از مقدار مرجع یا همان ۱۱ است.

واضح است که هر بیمار، با توجه به اندازه‌گیری ماهانه، باید شش اندازه مختلف داشته باشد، مگر آنکه در یک یا چند ماه برای بررسی آماری، مراجعه نکرده باشد. در تصویر ۱، نمونه‌ای از اطلاعات این بیماران مشخص شده، هر چند تعداد ۶۱ بیمار مورد بررسی قرار گرفته‌اند، ولی چون از هر بیمار بیش از یک بار اندازه‌گیری صورت گرفته، تعداد مشاهدات (سطرهای کاربرگ) برابر با ۳۶۶ خواهد بود.

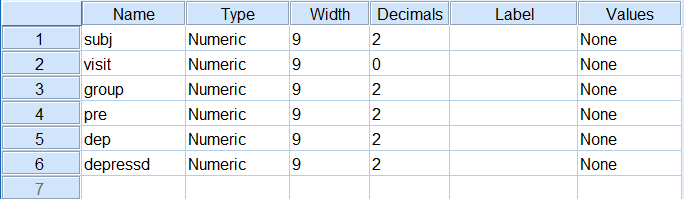
در تصویر ۲، نیز ساختار متغیرهای این مجموعه داده را در برگه Variable View مشاهده می‌کنید.

از آنجایی که برای استفاده از تکنیک GEE باید یک توزیع خاص را برای متغیر وابسته در نظر بگیریم، در این متن، از توزیع دو جمله‌ای کمک گرفته‌ایم. همچنین برای به دست آوردن مدل، «تابع پیوند» را «لوجیت» (logit) تنظیم خواهیم کرد. از طرفی از «ساختار ماتریس همبستگی» (Working Correlation Matrix) را با شیوه‌های مختلف معرفی کرده و برای مدل GEE استفاده می‌کنیم. به این ترتیب، برآورد پارامترهای مدل برای داده دو وضعیتی و تحلیل پانلی را به صورت‌های گوناگون انجام خواهیم داد.

داده دو وضعیتی و تحلیل پانلی با ساختار استقلال

کدی که در ادامه مشاهده می‌کنید، به منظور ایجاد یک مدل با تکنیک GEE با توجه به ساختار استقلال در ماتریس همبستگی، نوشته شده است.

1genlin depressd (reference = first) with visit group
2 /model visit group distribution = binomial link = logit
3 /repeated subject = subj
4 /print modelinfo cps solution workingcorr.
5            <div class="faradars-courses faradars-courses-single">
6                <a href="https://faradars.org/courses/statistical-software-spss-fvst9912?utm_source=blog.faradars&utm_medium=referral-post&utm_campaign=related-courses-inline-5&utm_term=a.reybod&utm_content=statistics" target="_blank">
7                    <div class="card card-course">
8                        <div class="card-image">
9                            <img class="pop-img" src="https://faradars.org/wp-content/uploads/2021/03/17/6051dd030c242-fvst9912-svg.svg" alt="آموزش نرم افزار اس پی اس اس SPSS">
10                        </div>
11                        <div class="card-body">
12                            <div class="card-title">
13                                فیلم آموزش نرم افزار اس پی اس اس SPSS در فرادرس
14                            </div>
15                        </div>
16                        <div class="card-action ml-3">
17                            <div class="fdb-btn">کلیک کنید</div>
18                        </div>
19                    </div>
20                </a>
21            </div>
22        

همانطور که می‌بینید، توزیع متغیر وابسته «دو جمله‌ای» (Binomial) در نظر گرفته شده و تابع پیوند نیز logit‌ است. پارامتر repeated نیز با متغیر subj‌ مقدار دهی شده است. همچنین «ساختار ماتریس همبستگی» (Working Correlation Matrix Structure) یا به نوعی «ماتریس واریانس کوواریانس» (Variance-Covariance Matrix)، با توجه به استقلال، ساخته شده که به طور پیش‌فرض در این دستور قرار دارد.

نکته: با توجه به ساختار ماتریس کوواریانس یا ماتریس همبستگی در تحلیل داده پانلی با تکنیک GEE، بهتر است نقش این ماتریس را در مطلب معادلات برآوردیابی تعمیم یافته (GEE) در آمار | به زبان ساده مطالعه کنید.

خروجی حاصل از این دستورات به صورت زیر است. ابتدا اطلاعات مدل طبق تصویر 3، ظاهر می‌شود.

توجه داشته باشید که مقدار ۱ برای متغیر پاسخ به سطح یا گروه اثر در نظر گرفته شده و مقدار صفر، نشانگر گروه مرجع یا کنترل است. به این ترتیب، بیمارانی که دارای اندازه افسردگی بیش از ۱۱ هستند با بیمارانی که میزان افسردگی آن‌ها کمتر از ۱۱ است، برحسب نوع تیمار و درمان به کار رفته، مقایسه می‌شوند.

مشاهدات معتبر و دارای مقدار گمشده نیز در جدول بعدی که با عنوان Case Processing Summary مشخص شده است، دیده می‌شوند. این جدول را در تصویر 4، می‌بینید. گزینه exclude نشانگر مشاهداتی که است که برای بعضی از سطرها از مجموعه داده، دارای مقدار گمشده است. این سطرها، هنگام محاسبه پارامترهای مدل، کنار گذاشته می‌شوند.

در ادامه نیز درست به مانند تصویر 5، داده‌های جدول «برآورد پارامترها» (Parameter Estimates) دیده می‌شوند که برای هر یک از متغیرهای visit و group یک ضریب را مشخص کرده است. با توجه به مقدار Sig هر دو این متغیرها، از لحاظ آماری، معنی‌دار هستند.

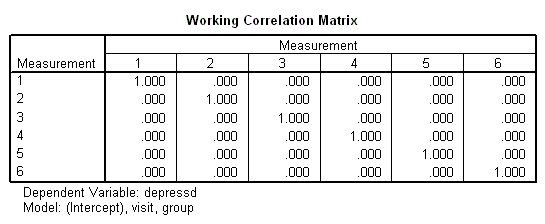
«ماتریس همبستگی» (Working Correlation Matrix) با توجه به شرط استقلال نیز به مانند تصویر 6، خواهد بود. واضح است که عناصر قطر اصلی همگی برابر با ۱ و خارج از قطر، صفر خواهند بود. صفر بودن عناصر خارج از قطر، نشانگر عدم وابستگی سطوح مختلف متغیر depressed است.

نکته: در داده‌های پانلی، اعتقاد داریم که متغیرهای وابسته، علاوه بر متغیرهای مستقل، با یکدیگر نیز وابستگی دارند.

داده دو وضعیتی و تحلیل پانلی با ساختار تعویض‌پذیر

این بار ساختار ماتریس کوواریانس را به صورت «تعویض‌پذیر» (Exchangeable) در نظر می‌گیریم و خروجی‌ها را مورد بررسی قرار می‌دهیم. کد مربوطه در ادامه دیده می‌شود.

1genlin depressd (reference = first) with visit group
2 /model visit group distribution = binomial link = logit
3 /repeated subject = subj corrtype = exchangeable
4 /print modelinfo cps solution workingcorr.

در ادامه فقط خروجی‌هایی که با قسمت‌های قبلی متفاوت هستند، آورده خواهد شد. در تصویر 7، که مربوط به معرفی مدل است، بخش Working Correlation Matrix Structure مقدار Exchangeable را نشان می‌دهد که نشان از تعویض‌پذیری ماتریس هبمستگی یا واریانس-کوواریانس دارد.

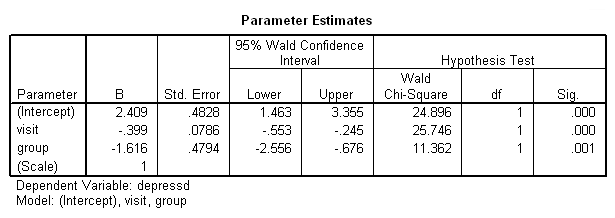
پارامترها نیز در جدول Parameter Estimates و مطابق با تصویر 8، قابل مشاهده‌اند. در اینجا هم همه پارامترها، معنی‌دار تلقی شده‌اند. زیرا مقدار Sig کوچکتر از ۰٫۰۵ است. از طرفی، همانطور که می‌بینید، هیچکدام از فاصله اطمینان‌های حاصل، شامل صفر نیستند. در نتیجه فرض صفر یا بی‌اثر بودن عامل‌ها، رد می‌شود. همچنین مشخص است که این فاصله‌های اطمینان، دارای کران‌های منفی هستند، درنتیجه اثر متغیرهای مربوطه روی متغیر وابسته، به شکل معکوس است.

این امر به این معنی است که با افزایش تعداد بازدیدها (visit) و تغییر از گروه کنترل به گروه درمان (تغییر از صفر به یک)، مقدار متغیر وابسته (میزان افسردگی) کاهش خواهد یافت.

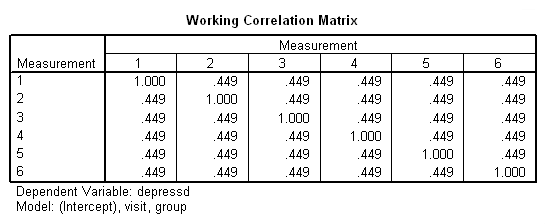
در تصویر 9 نیز خروجی Working Correlation Matrix را مشاهده می‌کنید که به ساختار ماتریس همبستگی اشاره دارد. تقارن بین همبستگی‌ها به طور کامل دیده می‌شود.

داده دو وضعیتی و تحلیل پانلی بدون ساختار برای ماتریس همبستگی

این بار در کد زیر، ماتریس همبستگی را بدون ساختار در نظر می‌گیریم. به این ترتیب همبستگی‌ها براساس مقادیر داده‌ها، برآورد خواهند شد.

1genlin depressd (reference = first) with visit group
2 /model visit group distribution = binomial link = logit
3 /repeated subject = subj corrtype = unstructured
4 /print modelinfo cps solution workingcorr.
5            <div class="faradars-courses faradars-courses-single">
6                <a href="https://faradars.org/courses/fvst9408-correlation-and-linear-regression-with-spss?utm_source=blog.faradars&utm_medium=referral-post&utm_campaign=related-courses-inline-5&utm_term=a.reybod&utm_content=statistics" target="_blank">
7                    <div class="card card-course">
8                        <div class="card-image">
9                            <img class="pop-img" src="https://faradars.org/wp-content/uploads/2015/11/fvst9408-svg.svg" alt="آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS">
10                        </div>
11                        <div class="card-body">
12                            <div class="card-title">
13                                فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس
14                            </div>
15                        </div>
16                        <div class="card-action ml-3">
17                            <div class="fdb-btn">کلیک کنید</div>
18                        </div>
19                    </div>
20                </a>
21            </div>
22        

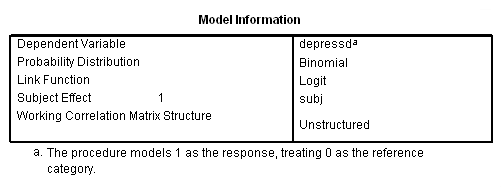
و خروجی‌ها را به صورت زیر دریافت می‌کنیم. بدون ساختار بودن توسط پارامتر Unstructured تعیین شده است.

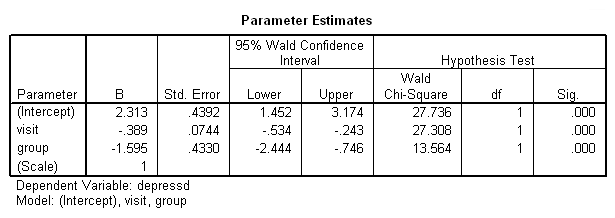
به این ترتیب برآورد پارامترهای مدل خطی بین متغیر وابسته و متغیرهای مستقل در تحلیل پانلی، مطابق با تصویر 11 و در جدول Parameter Estimates، ظاهر خواهند شد.

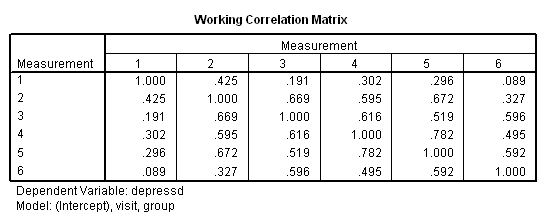
در تصویر ۱2 نیز ماتریس همبستگی را در حالت بدون ساختار مشاهده می‌کنید. هر خانه از این جدول، ضریب همبستگی بین متغیرها را به صورت برآورد شده، نشان می‌دهد.

داده دو وضعیتی و تحلیل پانلی با ساختار اتورگرسیو مرتبه اول

با توجه به خروجی‌های ظاهر شده در تصویر ۱2، به نظر می‌رسد که ماتریس همبستگی باید دارای ساختار اتورگرسیو مرتبه اول یا (AR(1 باشد. زیرا بیشترین همبستگی بین متغیرهای وابسته در یک سطح با سطح بعدی دیده می‌شود. مثلا اندازه ۳ با ۲، ۴ با ۵ یا ۱ با ۲، بیشترین همبستگی را دارد. بنابراین در گام بعدی از مدل «همبستگی سریالی» (Serial Correaltion) یا همان اتورگرسیو مرتبه اول، استفاده می‌کنیم.

1genlin depressd (reference = first) with visit group
2 /model visit group distribution = binomial link = logit
3 /repeated subject = subj withinsubject=visit corrtype = ar(1) covb=model
4 /print modelinfo cps solution workingcorr.

خروجی‌ها مطابق با تصاویر زیر ظاهر می‌شوند. مشخص است که مدل اتورگرسیو مرتبه اول برای ساختار ماتریس همبستگی به کار رفته است. برآوردها و ماتریس همبستگی نیز در ادامه دیده می‌شوند.

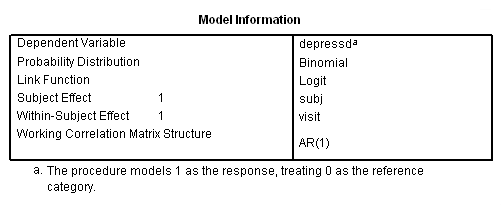
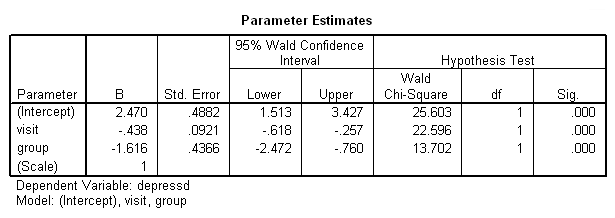
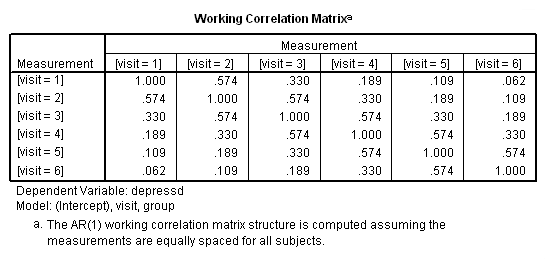
همچنین می‌توان خروجی را برحسب «اندازه نسبت بخت» (Odds ratio metric) و با انتخاب گزینه exponentiated ایجاد کرد. کدهای زیر به این منظور تهیه شده‌اند. به زیربخش print توجه کنید که در آن عبارت exponentiated به کار رفته است.

1genlin depressd (reference = first) with visit group
2 /model visit group distribution = binomial link = logit
3 /repeated subject = subj corrtype = ar(1)
4 /print solution (exponentiated) modelinfo.

بنابراین خروجی برای پارامترها تغییر کرده و مطابق با تصویر 16 خواهد بود.

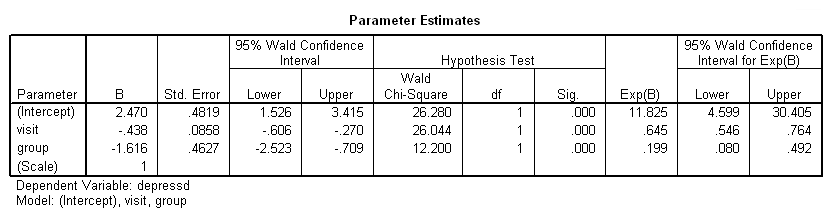
همانطور که مشخص است، همه متغیرها با معنی شده و همچنین ضرایب رابطه توانی نیز در قسمت (Exp(B دیده می‌شوند. برای هر یک از ضرایب نیز یک ستون برای کران پایین (Lower) و یک ستون نیز برای کران بالای (Upper) فاصله اطمینان اختصاص یافته است.

فیلم آموزش تحلیل های رگرسیونی با اس پی اس اس SPSS در فرادرس

کلیک کنید

در گام بعدی متغیر pre و همچنین اثرات متقابل متغیر group را با متغیر visit‌ مبنا قرار می‌دهیم. به کد زیر توجه کنید. ابتدا حاصل ضرب group در visit محاسبه، سپس مدل GEE برازش شده است.

1compute gxv = group*visit.
2
3genlin depressd (reference = first) with pre group visit gxv
4 /model pre group visit gxv distribution = binomial link = logit
5 /repeated subject = subj corrtype = ar(1)
6 /print solution modelinfo.

نتیجه برای پارامترها به صورت زیر خواهد بود.

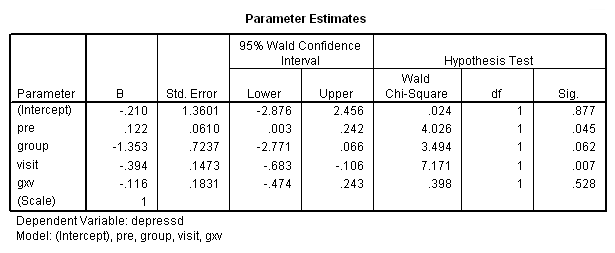
مشخص است که متغیر gxv که اثرات متقابل را اندازه‌گیری می‌کند، در مدل معنی‌دار نیست. در گام بعدی از متغیر طبقه‌ای visit استفاده خواهیم کرد. ابتدا این متغیر را به متغیرهای دو دویی دیگر تفکیک کرده تا به صورت یک مجموعه متغیر مجازی با نام‌های visit2 تا visit5، تبدیل شود. این کار را در قطعه کد زیر انجام داده‌ایم.

1compute visit2 = 0.
2if visit = 2 visit2 = 1.
3compute visit3 = 0.
4if visit = 3 visit3 = 1.
5compute visit4 = 0
6if visit = 4 visit4 = 1.
7compute visit5 = 0.
8if visit = 5 visit5 = 1.
9compute visit6 = 0.
10if visit = 6 visit6 = 1.
11exe.
12
13genlin depressd (reference = first) with pre group visit2 visit3 visit4 visit5 
14 /model pre group visit2 visit3 visit4 visit5 distribution = binomial link = logit
15 /repeated subject = subj corrtype = ar(1)
16 /print solution modelinfo.

به این ترتیب متغیرهای visit2‌ تا visit5 برای طراحی مدل به کار رفته‌اند. واضح است که هر کدام از این متغیرهای نشانگر،  با توجه به مقدار ۰ و ۱ اندازه گرفته و در هفته مورد نظر ساخته شده‌اند. توجه دارید که visit6 به علت فرض رابطه اتورگرسیو، حذف شده‌‌ است.

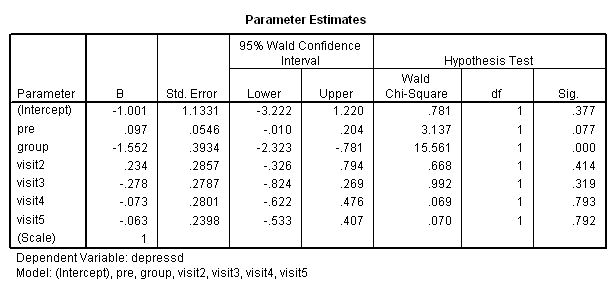
همانطور که در تصویر ۱8 دیده می‌شود، فقط متغیرهای group و pre برای داده دو وضعیتی و تحلیل پانلی معنی‌دار شده‌اند و بقیه متغیرها را می‌توان نادیده گرفت. در گام بعدی متغیر visit را نیز به این مدل اضافه می‌کنیم.

1genlin depressd (reference = first) with pre group visit visit2 visit3 visit4 visit5 
2 /model pre group visit visit2 visit3 visit4 visit5 distribution = binomial link = logit
3 /repeated subject = subj corrtype = ar(1)
4 /print solution modelinfo.

خروجی‌ها به صورت زیر خواهند بود.

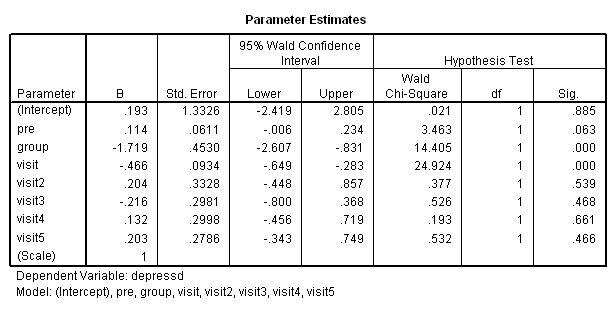
در جدول نمایش داده شده در تصویر ۱۹، متغیرهای group و visit معنی دار بوده و بقیه متغیرها از لحاظ آماری معنی‌دار نیستند. بنابراین تنها عامل‌هایی که روی بهبود بیماری افسردگی تاثیر گذار هستند، زمان‌های مربوط به متغیر visit و همچنین گروه درمانی یا group است. البته توجه دارید که این ضرایب منفی هستند و بنابراین تاثیر عکس در میزان افسردگی پس از زایمان بیماران دارند.

خلاصه و جمع‌بندی

در این نوشتار با نحوه اجرای روش GEE روی داده دو وضعیتی و تحلیل پانلی تمرکز کردیم و برای پیاده‌سازی محاسبات از کدهای دستوری نرم‌افزار SPSS کمک گرفتیم. البته در این بین به کمک مدل اتورگرسیو، بهترین برآوردها، حاصل شد. از طرفی به منظور نمایش اثرات متقابل نیز از متغیر کمکی استفاده کرده ولی نشان دادیم که اثرات متقابل متغیر group و visit روی متغیر وابسته (که به صورت دو دویی است) وجود ندارد. ساختارهای مختلفی نیز برای ماتریس همبستگی در نظر گرفته شد که بهترین مدل از طریق ساختار اتورگرسیو مرتبه اول برای داده دو وضعیتی و تحلیل پانلی مثال مورد نظر ایجاد گردید. این امر به علت ساختار موجود در داده‌ها بوجود آمد که در ماتریس همبستگی بدون ساختار مشخص شده بود.