داده‌ پانلی (Panel Data) — از صفر تا صد

داده‌ پانلی (Panel Data) در تحلیل‌های آماری بخصوص در اقتصاد سنجی (Econometric) به مجموعه اطلاعاتی گفته می‌شود که چند بُعدی (Multidimensional) بوده و در مقاطع زمانی مختلف اندازه‌گیری می‌شوند. به این ترتیب به تحلیل‌هایی که روی داده‌ پانلی صورت می‌گیرد، تحلیل‌های پانلی (Panel Analysis) نیز گفته می‌شود. از همین رو و بر اساس آنچه گفته شد می‌توان داده پانلی را به نوعی داده مکان-زمان (Spacial-Time Data) نیز در نظر گرفت.

شناخت داده پانلی و نحوه تحلیل آن بخصوص برای کسانی که در حوزه یادگیری ماشین (Machine Learning) و علم داده (Data Science) فعالیت می‌کنند ضروری است تا به کمک این تکنیک آماری قادر به تجزیه و تحلیل پدیده‌های تصادفی شوند.

برای آشنایی بیشتر با انواع داده بهتر است مطلب جامعه آماری — انواع داده و مقیاس‌های آن‌ها را مطالعه کنید. همچنین برای درک تکنیک‌هایی که در تحلیل داده‌های پانلی انجام می‌شود خواندن نوشتارهای رگرسیون خطی — مفهوم و محاسبات به زبان ساده و تحلیل سری زمانی — تعریف و مفاهیم اولیه نیز خالی از لطف نیست.

داده‌ پانلی

داده پانلی (Panel Data) که در برخی موارد به عنوان داده طولی (Longitude) یا مقطع-متقابل سری زمانی (Cross-Sectional Time Series) نیز شناخته می‌شوند، داده‌هایی هستند که از تعداد مشاهدات معمولاً اندک در مقاطع طولانی زمانی تولید می‌شوند.

فیلم آموزش مبانی و روش های اقتصاد سنجی با ایویوز Eviews در فرادرس

کلیک کنید

داده پانلی شامل مشاهدات پدیده‌های تصادفی متعدد است که داده‌های آن در طی چندین دوره زمانی مختلف برای همان مشاهدات جمع‌آوری و ثبت شده است. در نتیجه می‌توان داده‌های سری زمانی (Time series Data) را حالت خاصی از داده‌های پانلی در نظر گرفت. از طرفی تحلیل سری زمانی نیز یکی از حالت‌های تحلیل داده‌ پانلی محسوب می‌شود زیرا در سری زمانی متغیر پاسخ یک بُعدی است در حالیکه داده‌ پانلی به صورت چند متغیره در نظر گرفته می‌شود.

نکته‌ای که داده‌ پانلی را دارای اهمیت می‌کند، وجود اثر متغیرهای عامل در یک مدل رگرسیونی است. این تاثرات ممکن است براساس یک اثر تصادفی (Random Effect) صورت گرفته باشد یا مدل تحت تاثیر یک متغیر عامل ثابت (Fixed Effect) باشد.

به این ترتیب تحلیل داده‌ پانلی درست به مانند یک تحلیل واریانس است که به صورت چند متغیره با یک تحلیل سری زمانی مخلوط و اثر عوامل تصادفی یا ثابت در مدل مورد بررسی قرار می‌گیرد.

مثال 1: فرض کنید داده‌های مربوط به افراد مختلف در یک جدول ثبت شده است که شامل درآمد و سن آن‌ها است. این متغیرها در طول زمان (year) تغییر می‌کنند. از طرفی ویژگی‌های انحصاری هر فرد در ستون شخص (person) و جنسیت (sex) نوشته شده است که در طول زمان تغییر نخواهند کرد. به نظر می‌رسد که ویژگی‌های نفر اول برای سال‌های ۲۰۱۶ تا ۲۰۱۸ ثبت شده است. همین عمل نیز برای فرد دوم صورت گرفته است.

$${\displaystyle {\begin{matrix}\mathrm {person} &\mathrm {year} &\mathrm {income} &\mathrm {age} &\mathrm {sex} \\1&2016&1300&27&1\\1&2017&1600&28&1\\1&2018&2000&29&1\\2&2016&2000&38&2\\2&2017&2300&39&2\\2&2018&2400&40&2\end{matrix}}}$$

داده پانلی متوازن (Balanced Panel Data)

چنین مجموعه‌ای از اطلاعات را داده‌ پانلی متوازن (Balanced Panel) می‌گویند، زیرا مشاهدات برای هر یک از افراد به صورت یکسان و در سه سال پیاپی ثبت شده است. در عوض اگر مجموعه داده‌ها به صورت زیر باشد، با داده پانلی نامتوازن (Unbalanced Panel Data) مواجه هستیم، زیرا تعداد مشاهدات برای هر یک از هویت‌ها برابر نیست.

$${\displaystyle {\begin{matrix}\mathrm {person} &\mathrm {year} &\mathrm {income} &\mathrm {age} &\mathrm {sex} \\1&2016&1600&23&1\\1&2017&1500&24&1\\2&2016&1900&41&2\\2&2017&2000&42&2\\2&2018&2100&43&2\\3&2017&3300&34&1\end{matrix}}}$$

(داده پانلی نامتوازن) Unbalanced Panel Data

همانطور که در مثال مشخص شد، داده‌ پانلی به صورت یک ماتریس $$N\times T$$‌ هستند که $$N$$‌ تعداد مشاهدات پانلی و $$T$$‌ نیز دوره است. بنابراین تعداد کل مشاهدات در داده‌های پانلی متوازن برابر است با $$n=N\times T$$. در حالیکه اگر داده‌های پانلی نامتوازن باشند، تعداد کل مشاهدات کمتر از این حاصل ضرب است پس داریم: $$n < N\times T$$

نکته: نحوه ورود داده‌های مثال بالا با «قالب طویل» (Long Format) است زیرا هر سطر مربوط به یک بار اندازه‌گیری است. ممکن است داده‌های پانلی در قالب عریض (Wide Format) ارائه شوند. به این ترتیب هر سطر بیانگر یک فرد خاص است که مقادیر مربوط به درآمد و سن او nv سال‌های ۲۰۱۶ تا ۲۰۱۸ در ستون‌های جداگانه‌ای ثبت شده‌اند.

مثال ۲: با توجه به داده‌های مثال ۱، قالب ارائه عریض برای این مجموعه داده به صورت زیر است.

$${\displaystyle \begin{matrix}\mathrm {person} &\mathrm {sex}&\mathrm {age-2016}&\mathrm {age-2017}&\mathrm {age-2018} &\mathrm {income-2016} &\mathrm {income-2017}&\mathrm {income-2018}\\1&1&23&24&-&1600&1500&-\\2&2&41&42&43&1900&2000&2100\\3&1&-&34&-&-&3300&-\end{matrix}}$$

دلایل استفاده از داده پانلی

همانطور که پیش از این اشاره شد، تحقیقاتی که به سری زمانی در حالت چند متغیره مرتبط است، می‌تواند محلی برای به کارگیری داده پانلی باشد. در ادامه لیستی از مزایای استفاده از داده پانلی نسبت به سری زمانی یا تحلیل رگرسیونی ارائه می‌شود.

1. داده‌ پانلی می‌تواند به طور صریح ناهمگونی داده‌های یک فرد خاص را هم در نظر بگیرد. این کار درست به مانند تحلیل واریانس بر اساس داده‌های تکراری (Repeated Measure Anova) است. منظورمان از فرد، یک هویت است که در طول تحقیق ثابت می‌ماند ولی بعضی از ویژگی‌های آن در طول زمان تغییر خواهند یافت.
2. در داده پانلی، با ترکیب داده‌ها در دو بعد، امکان بررسی تغییرات داده‌ها بوجود آمده و در عین حال مشکل هم‌خطی (Colinearity) نیز کاهش می‌یابد. از طرفی درجه آزادی آماره آزمون نیز در تحلیل‌ها نسبت به حالت سری زمانی یا تحلیل واریانس، افزایش خواهد داشت.
3. در تحلیل داده پانلی، تشخیص و اندازه‌گیری اثرات عوامل ثابت و تصادفی نسبت به مدل تحلیل واریانس یا سری زمانی دقیق‌تر است.
4. داده پانلی و تحلیل پانلی، امکان مطالعه مدل‌های رفتاری پیچیده‌تر را فراهم می‌آورند. به عنوان مثال اثرات تغییر تکنولوژی یا چرخه اقتصادی را روی میزان گردش مالی شرکت‌ها امکان‌پذیر می‌سازند.

مدل‌های داده پانلی

متغیرهای پیشگو (Predictor Variable) در یک تحلیل داده‌ پانلی معمولا به صورت زیر در نظر گرفته می‌شوند.

$$\large {\displaystyle X_{it},\quad i=1,\dots ,N,\quad t=1,\dots ,T,}$$

در اینجا، $$i$$ نشانگر بُعد است و $$t$$‌ نیز بُعد زمان را نشان می‌دهد. اگر به دنبال ایجاد یک مدل رگرسیونی روی داده‌ پانلی هستید، رابطه زیر می‌تواند مفید به نظر آید.

$$\large y_{it}=\alpha +\beta 'X_{it}+u_{it},\\ \large{\displaystyle u_{it}=\mu _{i}+v_{it}}$$

متغیر $$\mu_i$$ اثری است که وابسته به زمان نبوده و آن را می‌توان متغیر با اثر ثابت در نظر گرفت که فقط با تغییر بُعد تغییر می‌کند. برای مثال می‌توان در تحلیل‌های داده‌های کشوری این متغیرها را وضعیت آب و هوا یا مختصات جغرافیایی در نظر گرفت.

در مقابل متغیر $$\nu_{it}$$ متغیری است که مقادیر آن وابسته به زمان است. برای این جمله در هر واحد زمانی، یک توزیع نرمال با میانگین صفر و واریانس $$\sigma^2$$ در نظر گرفته می‌شود.

$$\large \nu_{it}\sim N(0,\sigma^2)$$

اگر $$\mu_i$$ با حداقل یکی از متغیرهای مستقل وابستگی داشته باشد، باعث اریبی در روش رگرسیون خطی مثلا حداقل مربعات عادی (OLS) می‌شود. هر چند با استفاده از روش داده پانلی و در نظر گرفتن برآوردگر اثرات ثابت یا برآوردگر اولین تفاضل (First-difference Estimator) می‌توان اثر این اریبی را کنترل کرد.

اگر $$\mu_i$$ با هیچ یک از متغیرهای مستقل وابستگی نداشته باشد، می‌توان برای انجام برآوردهای غیرمستقیم و سازگار از پارامترهای رگرسیون استفاده کرد. اما، به دلیل اینکه $$\mu_i$$ با گذشت زمان ثابت در نظر گرفته شده است، باعث می‌شود همبستگی سریالی (Serial Correlation) در جمله خطای رگرسیون بوجود آید.

مدل اثرات تصادفی (Random Effect Model) یکی از روش‌هایی است که به صورت خاصی از حداقل مربعات استفاده می‌کند، بطوری که ساختار همبستگی سریالی ناشی از $$\mu_i$$ را کنترل کند. چنین ساختارهایی برای داده پانلی را می‌توان ایستا (Static) در نظر گرفت، زیرا مقادیر متغیر وابسته با یکدیگر همبستگی ندارند. به این ترتیب می‌توان مدل‌های متفاوتی برای تحلیل داده‌ پانلی به صورت ایستا در نظر گرفت.

مدل استقلال آمیخته (Independently Pooled Panels)

در این مدل فرضیه کلیدی آن است که ویژگی‌های منحصر به فردی از مشاهدات وجود ندارد که در طول زمان ثابت نباشند. از طرفی مدل تحت تاثیر زمان قرار ندارد.

مدل اثرات ثابت (Fixed Effect Model)

در این مدل فرضیه کلیدی آن است که ویژگی‌های منحصر به فردی از مشاهدات وجود دارند که در طول زمان متفاوت نیستند. این ویژگی‌ها ممکن است با متغیرهای وابسته به هر مشاهده در ارتباط باشند یا نباشند. برای آزمایش اینکه آیا اثرات ثابت به جای تأثیرات تصادفی مورد نیاز است، می‌توان از آزمون «وو-هوسمن» (Wu-Haussman) استفاده کرد.

مدل اثرات تصادفی (Random Effect Models)

در این مدل فرضیه کلیدی آن است که متغیرهای مربوط به مشاهدات وابسته به زمان نیستند و از طرفی وابستگی بین متغیرهای پیشگو (Regressor) وجود ندارد. مدل رگرسیون خطی عادی آمیخته (Pooled OLS) می‌تواند در این بین برآوردگرهای مناسب نااریب برای پارامترهای چنین مدلی را فراهم کند.

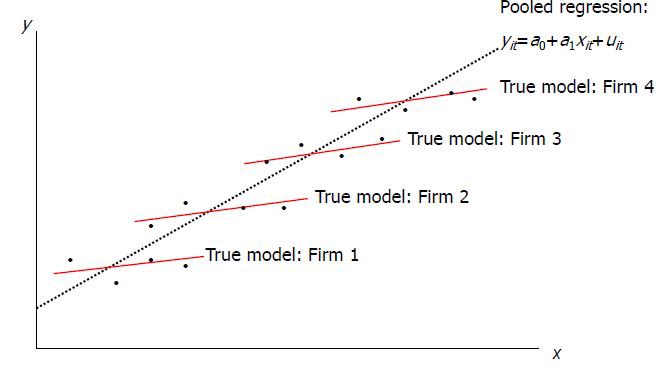
 مدل داده پانلی پویا

اگر داده‌ پانلی در زمان $$t$$ وابسته به زمان قبلی هم باشد، با یک مدل داده پانلی به صورت پویا مواجه شده‌ایم. در این حالت بین مقدار جاری و مقدار قبلی یک وقفه یا تاخیر (lag) وجود دارد. در مدلی که در ادامه مشاهده می‌کنید مقدار این تاخیر برابر با ۱ واحد زمانی است.

$$\large {\displaystyle y_{it}=\alpha +\beta 'X_{it}+\gamma y_{it-1}+u_{it}}$$

به این ترتیب شرط استقلال بین مشاهدات از بین می‌رود و مشخص است که مشاهده $$i$$ام با مشاهده قبلی براساس تاخیر مشخصی، مرتبط است. این نکته به صورت یک سری زمانی نیز قابل ارائه است.

در این میان «مدل‌ آمیخته گاوسی» (Gaussian Mixture Model) یا GMM بسیار به کار گرفته می‌شود.

تحلیل داده‌ پانلی

هنگام انجام تحلیل داده پانلی، با تکنیک‌ها یا محاسبات خاصی مواجه می‌شوید که در این بین بهتر است با بعضی از آن‌ها آشنا شویم.

فیلم آموزش اقتصاد سنجی در فرادرس

کلیک کنید

آزمون هوسمن (Hausman Test)

معنی‌داری اختلاف بین برآورد ضریب به دست آمده توسط مدل اثرات ثابت و اثرات تصادفی، توسط آزمون هوسمن صورت می‌پذیرد. در فرض صفر این آزمون فرض بر اثر بخش بودن مدل اثرات تصادفی در تحلیل داده‌ها است و در مقابل بی‌اثر بودن مدل اثرات ثابت است. این آزمون و آماره آن که با $$W$$ نشان داده می‌شود، شبیه آزمون والد (Wald Test) است و آماره آن دارای توزیع کای ۲ با $$k-1$$ درجه آزادی است. توجه داشته باشید که $$k$$ همان تعداد متغیرهای پیشگو را مشخص می‌کند.

اگر $$W$$ کوچکتر از مقدار بحرانی این آزمون باشد، فرض صفر رد شده و مدل اثرات تصادفی نسبت به مدل اثرات ثابت ترجیح دارد.

خودهمبستگی (Autocorrelation)

خودهمبستگی نشانگر وجود وابستگی بین مشاهدات در مقاطع مختلف زمانی است. خودهمبستگی یکی از مشکلاتی است که در تحلیل رگرسیون خطی عادی یا OLS ممکن است بوجود آید. یکی از روش‌های تشخیص خودهمبستگی استفاده از آزمون دوربین واتسون (Durbin-Waston) است.

برای اصلاح خودهمبستگی می‌توانیم از روشهای معمول مانند مدل تصحیح خطا یا هموارسازی را به کار بگیریم. در مدل‌های پویا نیز به کارگیری یک متغیر وابسته برحسب تاخیر (Lag) برای از بین بردن خودهمبستگی موثر است.

ناهم‌واریانسی

زمانی که با داده‌های پانلی بخشی (Cross-Section Panel Data) کار می‌کنیم، همیشه این احتمال وجود دارد که واریانس در بخش یا گروه‌هایی یکسان و برابر نباشد. البته آزمون‌هایی مانند آزمون لون (Leven's Test) برای تشخیص برابری واریانس در بین گروه‌ها قابل اجرا است.

مثال ۳: فرض کنیم داده‌های مربوط به شاخص سهام بیست کشور به صورت سالانه و در یک بازه زمانی ۱۰ ساله ثبت شده است. به این ترتیب ۲۰۰ مشاهده جمع آوری شده است. یک مدل برای این داده‌ها می‌تواند به صورت زیر باشد. در این مدل مقدار شاخص سهام ($$S_t$$) به صورت یک متغیر وابسته و هزینه تحقیقات در این کشورها ($$r_t$$) نیز متغیر مستقل در نظر گرفته شده است. برآورد این مدل و پارامترهای آن به شکل زیر درآمده است.

$$\large \widehat{S}_t=0.7+0.9r_t$$

مقدار ضریب تعیین ($$R^2$$) در این مدل برابر با 0٫7 و مقدار آماره دوربین-واتسون ($$DW$$) نیز 1٫98 به دست آمده است. در نتیجه می‌توان فرض استقلال باقی‌مانده را در نظر گرفت و از تحلیل پانلی با اثرات ثابت (Fixed Effect) استفاده کرد.

نکته: داده‌ها فرضی بوده و در این مثال فقط به نتایج حاصل از رگرسیونی خطی تکیه داریم.

معرفی فیلم آموزش برآورد مدل اقتصادسنجی ARDL با نرم افزار Eviews و Microfit

اغلب در رشته اقتصاد و مدیریت، از نرم افزارهای «ای ویوز» (EViews) و «میکروفیت» (Microfit) برای برآورد مدل‌های اقتصادسنجی استفاده می‌کنند. در نرم افزار EViews می‌توان با استفاده از داده‌های مقطعی، سری زمانی و همچنین پانلی به برآورد مدل های اقتصاد سنجی پرداخت. در مقابل نرم افزار میکروفیت یک نرم افزار تخصصی برای داده‌های سری زمانی است. از آنجایی که مدل «خودرگرسیونی» (Autoregressive) با وقفه های توزیعی (ARDL) یکی از پرکاربرد ترین مدل‌ها در تحلیل داده‌های پانلی محسوب می‌شود، توانایی برآورد این مدل‌ها در نرم افزارهای Eviews و میکروفیت اهمیت فراوانی برای دانشجویان و محققان دارد. آموزشی که قصد معرفی آن را داریم، به نحوه برآورد یک مدل ARDL روی داده‌های پانلی می‌پردازد. همچنین موضوعاتی نظیر آزمون‌هایی قبل و بعد از برآورد مدل نیز مورد بحث قرار خواهد گرفت. ضمن اینکه با برآورد مدل ARDL در دو نرم افزار EVeiws و Microfit محققان، می‌توانند چگونگی برآورد این مدل را در این دو نرم افزار پرکاربرد با یکدیگر مقایسه کرده و مورد بحث قرار دهند.

سرفصل مباحث آموزشی این فیلم به صورت زیر فهرست شده‌اند.

• درس یکم، معرفی انواع داده های اقتصادی در اقتصادسنجی: این بخش شامل مواردی مانند معرفی داده‌های مقطعی، داده‌های سری زمانی، داده‌های پانلی (Panel data) و همچنین مباحث مربوط به پایایی و آزمون‌های ریشه واحد سری زمانی است.
• درس دوم، معرفی الگوهای سری زمانی: در این درس به موضوعات مربوط به الگوهای خودرگرسیونی (AR)، خودرگرسیون میانگین متحرک (ARMA)، خودرگرسیون میانگین متحرک انباشته (ARIMA) پرداخته و مباحث خودرگرسیون برداری (VAR)، خودرگرسیونی با وقفه های توزیعی (ARDL) نیز مطرح می‌شوند.
• درس سوم، الگوهای خودرگرسیونی با وقفه های توزیعی: معرفی الگوی خودرگرسیونی با وقفه های توزیعی (ARDL)، الگوی اقتصاد سنجی کلی مدل‌‌های ARDL و  مزیت آن نسبت به سایر الگوهای اقتصادسنجی ارائه و با ذکر مثال‌‌هایی از این الگو برای حل مسائل اقتصاد سنجی استفاده می‌گردد.
• درس چهارم، برآورد الگوهای خودرگرسیونی با وقفه های توزیعی در EViews: شیوه استفاده از نرم‌افزار Eview برای حل مسائل اقتصاد سنجی با تکیه بر الگوی ARDL از مواردی است که در این درس با آن آشنا می‌شوید.
• درس پنجم، برآورد الگوهای خودرگرسیونی با وقفه های توزیعی در Microfit: به کارگیری نرم افزار Microfit و وارد کردن داده ها در آن، انتخاب وقفه بهینه در مدل های ARDL، برآورد مدل اقتصادسنجی براساس الگوی ARDL، انجام آزمون های پس از برآورد، آزمون هم انباشتگی (وجود رابطه بلندمدت)، آزمون هم‌ انباشتگی و برآورد الگوی تصحیح خطا در نرم‌افزار Microfit از مواردی است که در این درس به آن پرداخته شده است.

این آموزش برای کسانی که در رشته اقتصاد و مدیریت تحصیل و تحقیق می‌کنند، مناسب خواهد بود. این آموزش شامل دو ساعت پنچاه و نه دقیق محتوای فیلم ویدیوئی است.

توجه داشته باشید که برای این آموزش از نرم‌افزار‌های Mcrofit نسخه ۴٫۱ و Eviews نسخه ۹ استفاده شده است. درس‌های اقتصاد سنجی کلاسیک و همچنین آموزش مبانی و روش های اقتصاد سنجی با Eviews پیش‌نیازهای مربوط به این آموزش محسوب شده‌اند.

فیلم آموزش برآورد مدل اقتصادسنجی ARDL با ایویوز و میکروفیت Eviews و Microfit در فرادرس

کلیک کنید

خلاصه و جمع‌بندی

یک بخش از مهمترین بخش‌های تجزیه و تحلیل داده‌ پانلی، تصمیم برای انتخاب مدل اثرات ثابت (Fixed Effect) یا اثرات تصادفی (Random Effect) است. برای تشخیص این امر باید از «آزمون‌های «هاسمن» (Hausman) و «دوربین واتسون» (Durbin-Watson) استفاده کرد. داده‌ پانلی روشی برای تحلیل داده‌های سری زمانی و بخش‌بندی شده است. تکنیک‌های مختلفی در تجزیه و تحلیل داده‌ پانلی به کار گرفته می‌شوند. یکی دیگر از مسائلی که بخصوص در بررسی‌های سری‌زمانی باید تجزیه و تحلیل شود ایستایی (Stationary) است.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش‌های پیش‌بینی و تحلیل سری‌های زمانی
• آموزش متلب با نگرش تحلیل آماری، تحلیل سری های زمانی و داده های مکانی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• تابع خودهمبستگی (Autocorrelation Function) — مفاهیم و کاربردها
• آزمون والد (Wald Test) — مفهوم و کاربردها
• تابع درست نمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^