تابع نشانگر و خصوصیات آن — به زبان ساده

توابع (Functions) بخش زیاد و البته مهمی از ریاضیات را به خود اختصاص داده‌اند. در نوشتارهای دیگر مجله فرادرس در مورد چند نوع تابع پرکاربرد در ریاضیات و مهندسی صحبت کرده‌ایم. در اینجا اما به تابع نشانگر (Indicator Function) خواهیم پرداخت که بخصوص برای تبدیل یک متغیر پیوسته به متغیر گسسته کاربرد دارد. به این ترتیب می‌توان تابع نشانگر را به عنوان یک تابع دو وضعیتی یا دو ضابطه‌ای در نظر بگیریم.

برای آشنایی بیشتر با تابع و تعریف و خصوصیات آن رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده و مفاهیم تابع – به زبان ساده را مطالعه کنید. همچنین خواندن مطالب مجموعه ها در ریاضیات – مفاهیم پایه  و ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده نیز خالی از لطف نیست.

تابع نشانگر یا تابع مشخصه

در ریاضیات، تابع نشانگر (Indicator Function) یا «تابع مشخصه» (Characteristics Function) روی مجموعه مقادیری مثل $$X$$ تعریف می‌شود که بیانگر تعلق هر عنصر به یک مجموعه مثل $$A$$ است. به این ترتیب مقدار این تابع برای مقادیری از $$X$$ که عضو $$A$$ هستند برابر با ۱ و برای مقادیر خارج از $$A$$، برابر با صفر خواهد بود.

فیلم آموزش نظریه مجموعه های فازی و کاربردهای آن در فرادرس

کلیک کنید

چنین تابعی را معمولا با حرف $$I$$ لاتین یا $$1$$ نشان می‌دهند. در زبان علم کامپیوتر، تابع نشانگر را همان تابع گزاره بولی (Boolean predicate function) می‌نامند.

نکته: «تابع دریکله» (Dirichlet Function) نوعی تابع نشانگر است که بیانگر گویا بودن یک عدد است.

تعریف تابع نشانگر یا مشخصه

تابع نشانگر روی مجموعه $$A$$ از $$X$$ به صورت زیر نشان داده می‌شود. واضح است که دامنه این تابع $$X$$ بوده و برد آن مجموعه صفر و یک است. اندیس $$A$$ در اینجا به معنی وابستگی تابع نشانگر به مجموعه $$A$$ است.

$$\large {\displaystyle \text {1} _{A}\colon X\to \{0,1\}}$$

به این ترتیب هر گاه عضوی از مجموعه $$x \in X$$ در مجموعه $$A$$ نیز وجود داشته باشد، مقدار تابع نشانگر برابر با ۱ و در غیراینصورت، مقدار تابع برای آن برابر با صفر است. چنین خصوصیتی به صورت یک تابع دو ضابطه‌ای و به شکل زیر نوشته می‌شود.

$$\large {\displaystyle \text {1} _{A}(x):={\begin{cases}1&{\text{if }}x\in A,\\0&{\text{if }}x\notin A.\end{cases}}}$$

نکته: برای نمایش تابع نشانگر گاهی از نماد $$[x \in A]$$ نیز استفاده می‌کنند که معادل با $$\text{1}_{(x)}$$ است. همچنین نمادهای $$I_A$$، یا $$\chi_A$$ نیز از روش‌های مختلف نمایش تابع نشانگر هستند.

مجموعه همه توابع نشانگر روی مجموعه $$X$$ را به صورت مجموعه توانی $$P(X)$$ نشان می‌دهند. به یاد دارید که مجموعه توانی (Power Set) شامل همه زیرمجموعه‌های یک مجموعه است.

در تصویر ۱، نمایشی از یک تابع نشانگر روی مختصات دکارتی را مشاهده می‌کنید که به صورت زیر تعریف شده است.

$$\large {\displaystyle \text {1} _{[0,10]}(x):={\begin{cases}1&{\text{if }}x\in [0,10],\\0&{\text{if }}x\notin [0,10].\end{cases}}}$$

واضح است که در اینجا $$A = [0,10]$$ و $$X$$ مجموعه اعداد حقیقی است. هرگاه مقداری در بازه ۰ تا ۱۰ قرار گرفته باشد، تابع نشانگر مقدار ۱ و در غیر اینصورت مقدار صفر خواهد داشت.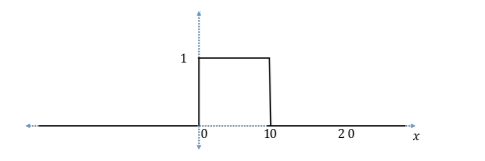

تصویر ۱: نمایش تابع نشانگر یک بُعدی روی محور مختصات دکارتی

خصوصیات پایه و اساسی تابع نشانگر

گستردگی تابع نشانگر از آمار و احتمال گرفته تا آنالیز ریاضی و حتی ریاضیات فازی گسترده است. تابع نشانگر یا مشخصه، خصوصیات جالبی دارد که در ادامه این متن به آن‌ها خواهیم پرداخت. همانطور که گفتیم، این تابع یک نگاشت از عناصر مجموعه $$X$$ به دو مقدار صفر و یک ایجاد می‌کند.

فیلم آموزش کنترل کیفیت آماری – جامع و با نکات کاربردی در فرادرس

کلیک کنید

چنین نگاشتی تنها زمانی دو طرفه (یک به یک و پوشا) است اگر $$A$$ یک زیر مجموعه صریح از $$X$$ بوده و در صورتی که $$X \equiv A$$ باشد، آنگاه $$1_A=1$$ خواهد بود. از طرفی برای هر مجموعه $$A \equiv \emptyset$$ خواهیم داشت $$1_A = 0$$.

در ادامه این متن، علامت $$\cdot$$ نشانگر ضرب است یعنی $$1 \cdot 1 = 1 , 1 \cdot 0 = 0$$ و + همچنین - نیز بیانگر جمع و تفریق است. همچنین $$\cap$$ و $$\cup$$ نیز به ترتیب اشتراک و اجتماع را نشان می‌دهند.

بنابراین اگر $$A$$ و $$B$$ دو زیرمجموعه از $$X$$ باشند، آنگاه:

$$\large {\displaystyle \text {1} _{A\cap B}=\min\{\text {1} _{A},\text {1} _{B}\}=\text {1} _{A}\cdot \text {1} _{B}}, \\ \large {\displaystyle \text {1} _{A\cup B}=\max\{{\text {1} _{A},\text {1} _{B}}\}=\text {1} _{A}+\text {1} _{B}-\text {1} _{A}\cdot \text {1} _{B}}$$

به عنوان یک تعریف کلی اگر $$A_1, \ldots , A_n$$ زیرمجموعه‌هایی از $$X$$ باشند، آنگاه برای هر $$x \in X$$ رابطه زیر که براساس حاصلضرب صفرها و یک‌ها ساخته می‌شود، زمانی که برابر با مقدار ۱ باشد، نشانگر آن است که $$x \in X$$ در همه $$A_i$$ها وجود دارد.

$$\large\prod _{k\in I}(\text {1} _{A_{k}}(x))$$

همچنین تابع نشانگر متمم مجموعه $$A$$ که به صورت $$A^c$$ نشان داده می‌شود و به شکل زیر قابل محاسبه است.

$$\large \displaystyle \text {1} _{A^{\complement }}=1-\text {1} _{A}$$

از طرفی اگر $$A_1, \ldots , A_n$$ زیرمجموعه‌هایی از $$X$$ باشند، آنگاه برای هر $$x \in X$$ رابطه زیر بیانگر حاصلضرب صفرها و یک‌ها است که اگر حاصل آن برابر با ۱ باشد، بیانگر آن است که $$x \in X$$ در هیچ یک از مجموعه‌های $$A$$ قرار ندارد.

$$\large\prod _{k\in I}(1-\text {1} _{A_{k}}(x))$$

براساس نگارش اجتماع مجموعه‌ها، رابطه بالا را به صورت زیر نیز می‌توان نشان داد.

$$\large \prod _{k\in I}(1-\text {1} _{A_{k}})=\text {1} _{X-\bigcup _{k}A_{k}}=1-\text {1} _{\bigcup _{k}A_{k}}$$

با باز کردن سمت چپ رابطه بالا، محاسبات به شکل زیر در خواهد آمد که در آن $$F$$ عدد کاردینال یا عدد اصلی (Cardinal number) مجموعه $$F$$ است. این شیوه نمایش یکی از شکل‌های نمایش اصل شمول و عدم شمول (Inclusion-Exclusion) است.

$$\large\text {1} _{\bigcup _{k}A_{k}}=1-\sum _{F\subseteq \{1,2,\dotsc ,n\}}(-1)^{|F|}\text {1} _{\bigcap _{F}A_{k}}=\sum _{\emptyset \neq F\subseteq \{1,2,\dotsc ,n\}}(-1)^{|F|+1}\text {1} _{\bigcap _{F}A_{k}}$$

همچنین از توابع نشانگر در حساب ترکیبیات نیز استفاده می‌شود. ضمناً از این تابع در «نظریه احتمال» (Probability Theory) نیز برای نشان دادن احتمال برحسب امید ریاضی متغیر تصادفی بهره می‌گیرند.

فرض کنید که $$X$$ یک فضای احتمال با اندازه احتمال $$P$$ باشد بطوری که $$A$$ یک مجموعه اندازه‌پذیر است. در این صورت $$1_A$$ یک متغیر تصادفی خواهد بود و بین امید ریاضی این متغیر تصادفی و تابع احتمال رخداد $$A$$ رابطه زیر برقرار می‌شود.

$$\large {\displaystyle \operatorname {E} (\text {1} _{A})=\int _{X}\text {1} _{A}(x)\,d\operatorname {P} =\int _{A}d\operatorname {P} =\operatorname {P} (A)}$$

به این ترتیب تابع احتمال یک پیشامد را برحسب امید ریاضی تابع نشانگر مربوط به آن پیشامد (که یک متغیر تصادفی است) نشان می‌دهند. در اثبات «نامساوی مارکف» (Markov Inequality) از این شکل تابع نشانگر برای ارتباط بین امید ریاضی و تابع احتمال استفاده می‌شود.

میانگین واریانس و کوواریانس متغیر تصادفی نشانگر

در این قسمت هم به خصوصیات تابع نشانگر به عنوان یک  متغیر تصادفی مرتبط با پیشامد $$A$$ می‌پردازیم. فضای احتمال $$(\Omega, F , P)$$ را در نظر بگیرید. متغیر تصادفی (Random Variable) نشانگر $$1_A$$ را به صورت $$1_A:\Omega \rightarrow R$$ و به شکل زیر تعریف می‌کنیم.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

اگر پیشامد $$\omega  \in A$$ رخ دهد، مقدار متغیر تصادفی برابر با ۱ است ($$1_A(\omega) = 1 , \text{if} \; \omega \in A$$) در غیر اینصورت متغیر تصادفی صفر خواهد بود.

برای چنین متغیری «امید ریاضی» (Expected Value- Mathematical Expecation) به صورت زیر محاسبه می‌شود.

$$\large\operatorname {E} (\text {1} _{A}(\omega ))=\operatorname {P} (A)$$

همچنین «واریانس» (Variance) نیز به شکل رابطه حاصل ضرب احتمال در متمم احتمال پیشامد $$A$$ خواهد بود. یعنی داریم:

$$\large\operatorname {Var} (\text {1} _{A}(\omega ))=\operatorname {P} (A)(1-\operatorname {P} (A))$$

اگر $$A$$ و $$B$$ دو پیشامد باشند، «کوواریانس» (Covariance) متغیرهای تصادفی نشانگر این دو پیشامد نیز به کمک رابطه زیر قابل محاسبه است.

$$\large \operatorname {Cov} (\text {1} _{A}(\omega ),\text {1} _{B}(\omega ))=\operatorname {P} (A\cap B)-\operatorname {P} (A)\operatorname {P} (B)$$

مشتق و انتگرال تابع نشانگر

تابع نشانگر که در تصویر ۱ دیده می‌شود، یک تابع پله‌ای است که یک طرف آن مقدار صفر و طرف دیگر پرشی به اندازه یک واحد دارد. از همین رو تابع نشانگر را از نوع «توابع پله‌ای هویساید» (Heaviside Step Function) می‌شناسند. چنین توابعی که با نماد $$H(x)$$ نشان داده می‌شوند، به عنوان توابع نشانگر یک بُعدی نیم خط مثبت شناخته می‌شوند، بطوری که دامنه آن‌ها بازه $$[0 , ]\infty)$$ است. این توابع به افتخار ریاضیدان انگلیسی «اولیور هویسیاید» (Oliver Heaviside) نام‌گذاری شده‌اند.

مشتق توزیعی این توابع را با «تابع دلتای دیراک» (Dirac Delta function) مشخص می‌کنند.

$$\large {\displaystyle \delta (x)={\tfrac {dH(x)}{dx}}}$$

در رابطه بالا $$\delta(x)$$  همان تابع دلتای دیراک است که مشتق تابع نشانگر برحسب $$x$$ خواهد بود. واضح است که بر این اساس تساوی انتگرالی زیر برقرار خواهد بود.

$$\large \int _{-\infty }^{\infty }f(x)\,\delta (x)dx=f(0)$$

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

مشتق تابع پله‌ای Heaviside را می‌توان به عنوان «مشتق طبیعی» در «مرز» دامنه که توسط نیمه-خط مثبت مشاهده می‌شود، نشان داد. در ابعاد بالاتر، مشتق طبیعی به مشتق عادی درونی (Inward Normal Derivative) تعمیم می‌یابد، در حالی که تابع پله‌ای Heaviside به طور طبیعی به تابع نشانگر روی دامنه $$D$$ تعمیم می‌یابد. سطح D در این حالت با نماد S مشخص می‌شود. در این صورت مشتق را برحسب تابع دلتای دیراک روی سطح $$s$$ مشخص می‌کنند. در این حالت داریم:

$$\large \delta _{S}(\text {x} )=-\text {n} _{x}\cdot \nabla _{x}\text {1} _{\text {x} \in D}$$

توجه داشته باشید که $$n$$ سطح خارجی $$s$$ است. سطح تابع دلتا در رابطه انتگرالی زیر صدق می‌کند.

$$\large -\int _{\text {R} ^{n}}f(\text {x} )\,\text {n} _{x}\cdot \nabla _{x}\text {1} _{\text {x} \in D}\;d^{n}\text {x} =\oint _{S}\,f(\beta  )\;d^{n-1}\beta$$

با در نظر گرفتن تابع $$f$$ برابر با یک، مشتق نرمال درونی تابع نشانگر، انتگرال عددی سطح $$s$$ خواهد بود.

نکته: نماد $$\oint$$ نشانگر انتگرال روی سطح است.

تابع مشخصه در نظریه مجموعه‌های فازی

در ریاضیات کلاسیک، توابع مشخصه مجموعه‌ها فقط مقادیر 1 (اعضا) یا 0 (غیر عضو) را به خود اختصاص می‌دهند. در «نظریه مجموعه‌های فازی» (Fuzzy set Theory)، توابع مشخصه حالت عمومی‌تری دارند بطوری که ارزش یا مقدار آن‌ها در فاصله‌ای به طول واحد مثلا [0 ، 1]  تعیین می‌شود. چنین توابع مشخصه تعمیم یافته (Generalized Characteristic Functions) معمولاً توابع عضویت (Membership Function) نامیده می‌شوند و «مجموعه» مربوطه ($$A$$) مجموعه فازی نامیده می‌شود. مجموعه‌های فازی، در بیان بسیاری از پدیده‌ها که دارای چندین سطح از مقدار هستند به کار گرفته می‌شوند. برای مثال تغییرات تدریجی در درجه عضویت را می‌توان برای نمایش قد بلند، گرما و ... به کار برد.

خلاصه و جمع‌بندی

در این نوشتار با تابع نشانگر یا تابع مشخصه و خصوصیات آن آشنا شدیم. از آنجایی که برد این تابع مربوط به اعداد صحیح است، نقش مهمی در نظریه اعداد داشته و همچنین در محاسباتی که باید یک متغیر کمی را به کیفی تبدیل کنند، به کار می‌رود. کاربردهایی مختلف این تابع در ریاضیات، آمار و احتمالات و همچنین در فیزیک نیز در این متن مورد توجه قرار گرفت. شیوه‌های مختلفی نیز برای نمایش تابع نشانگر استفاده می‌شود که در این متن به آن‌ها نیز اشاره شده است. هر چند محاسبات مربوط به تابع نشانگر، ساده به نظر می‌رسد ولی نقش مهمی در ریاضیات بازی می‌کند.