انواع زاویه چیست؟ — معرفی تمام زاویه ها — به زبان ساده

زاویه‌ها بر اساس معیارهای مختلف به انواع تند، باز، راست، نیم‌صفحه، کاو، تمام‌صفحه، مثبت، منفی، متمم، مکمل، مجاور، جفت خطی، متقابل به راس، متناظر و متبادل تقسیم می‌شوند. هر یک از این موارد، ویژگی‌های مختص به خود را دارند. در این مقاله، قصد داریم به معرفی انواع زاویه و نحوه تشخیص آن‌ها بپردازیم. علاوه بر این، انواع زاویه‌های موجود در چندضلعی‌ها و دایره را نیز مورد بررسی قرار می‌دهیم.

زاویه چیست؟

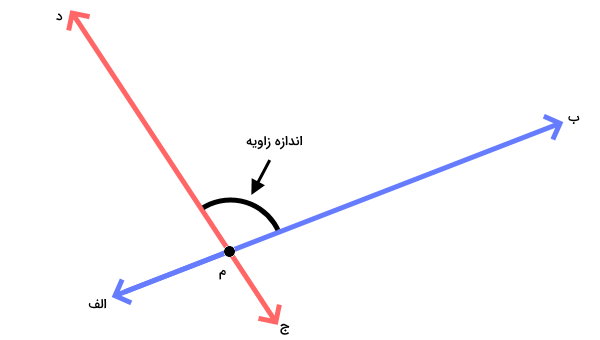
به فضای بین دو خط یا سطح متقاطع، زاویه می‌گویند. شکل زیر، زاویه بین دو نیم‌خط را نمایش می‌دهد. زاویه‌ها، اندازه زاویه‌ها، معمولا توسط یکای درجه یا رادیان بیان می‌شود.

برای درک بهتر مفهوم زاویه، عقربه‌های ساعت را در نظر بگیرید. فرض کنید عقربه بزرگ ساعت بر روی عدد ۱۲ قرار دارد. با گذشت زمان، موقعیت فعلی این عقربه تغییر می‌کند. هنگامی عقربه بزرگ که بر روی عدد ۲ قرار می‌گیرد، شکلی مشابه تصویر زیر به وجود می‌آید.

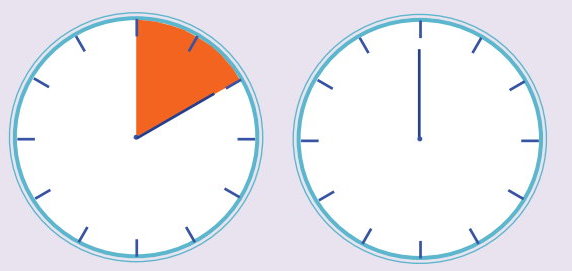
ناحیه رنگی در شکل سمت چپ، مسیر حرکت عقربه نسبت به موقعیت اولیه آن (شکل سمت راست) را نمایش می‌دهد. این ناحیه، بیانگر زاویه بین عدد 12 تا 2 است. با حرکت عقربه، زاویه آن نسبت به موقعیت اولیه تغییر می‌کند. اگر عقربه ساعت یک دور کامل بزند و به محل اولیه خود برسد، می‌گوییم ۳۶۰ درجه چرخیده است.

اجزای زاویه چه هستند؟

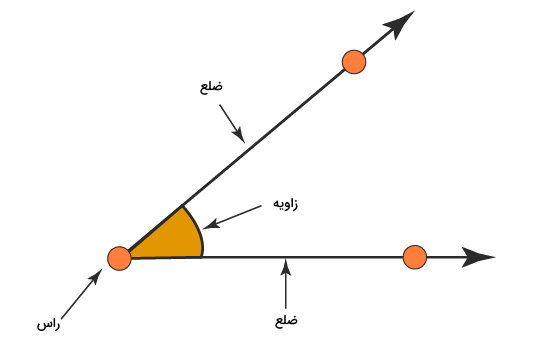
هر زاویه از یک راس و دو ضلع (نیم‌خط) تشکیل می‌شود:

• راس: نقطه اشتراک بین ضلع‌ها
• ضلع: دو نیم‌خط گذرنده از راس

اگر یک نیم‌خط را حول نقطه ابتدایی آن دوران دهیم، بین موقعیت اولیه و ثانویه نیم‌خط، یک زاویه به وجود می‌آید. با باز و بسته شدن ضلع‌ها، اندازه زاویه، کم و زیاد می‌شود (مانند عقربه‌های ساعت).

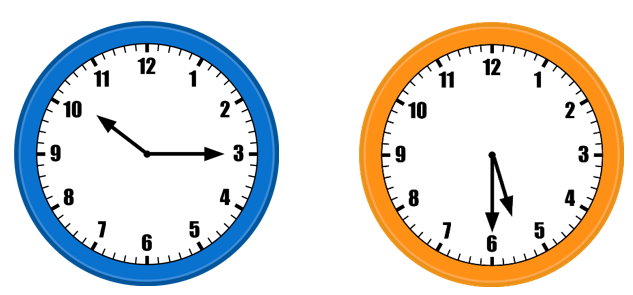
در یک ساعت، نقطه مشترک بین دو عقربه بزرگ و کوچک را می‌توان به عنوان راس زاویه در نظر گرفت. به این ترتیب، هر یک از عقربه‌ها، یکی از ضلع‌های زاویه محسوب می‌شوند. تغییر مکان ضلع‌ها نسبت به یکدیگر، اندازه زاویه را تغییر می‌دهد. به عنوان مثال، زاویه بین عقربه‌ها در ساعت 5 و 30 دقیقه، کمتر از این زاویه در ساعت 2 و 50 دقیقه است (تصویر زیر).

انواع زاویه چه هستند؟

معیارهای مختلفی برای دسته‌بندی انواع زاویه وجود دارد. این دسته‌بندی‌ها عبارت هستند از:

• انواع زاویه بر اساس اندازه زاویه
  • زاویه صفر
  • زاویه تند
  • زاویه راست
  • زاویه باز
  • زاویه نیم صفحه
  • زاویه مقعر
  • زاویه تمام صفحه
• انواع زاویه بر اساس جهت اندازه گیری
  • زاویه مثبت
  • زاویه منفی
• انواع جفت زاویت
  • زاویه های متمم
  • زاویه های مکمل
  • جفت زاویه های خطی
  • زاویه های مجاور
  • زاویه های متقابل به راس

در ادامه، هر یک از انواع زاویه‌های بالا را به همراه مثال و به صورت تصویری معرفی می‌کنیم.

انواع زاویه بر اساس اندازه

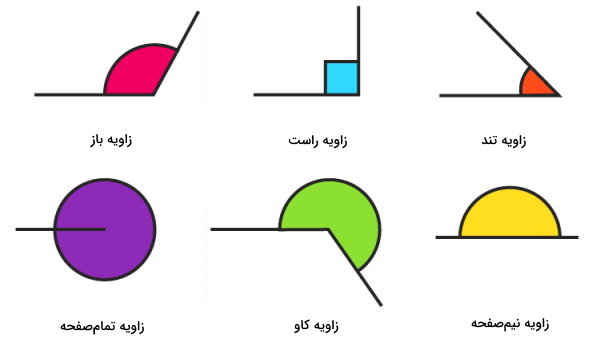
اولین معیار برای تقسیم‌بندی انواع زاویه، اندازه است. زاویه‌ها بر اساس اندازه به هفت نوع زاویه صفر، زاویه تند، زاویه راست، زاویه باز، زاویه نیم‌صفحه، زاویه کاو و زاویه تمام‌‌صفحه تقسیم می‌شود. تصویر زیر، شش مورد از این زاویه‌ها را نمایش می‌دهد.

زاویه تند چیست؟

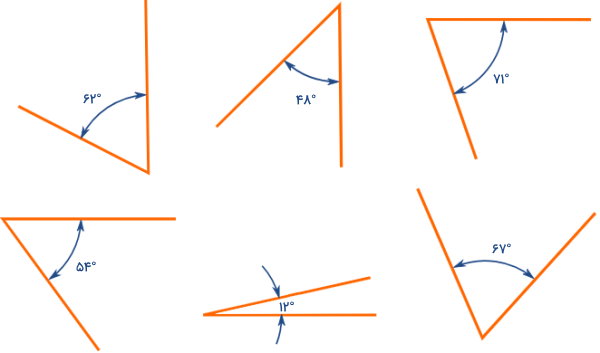
اندازه زاویه تند، کوچکتر از ۹۰ درجه است. این زاویه با عنوان زاویه حاده نیز شناخته می‌شود. گوشه‌های زاویه تند، تیزتر از دیگر انواع زاویه‌ها است. تصویر زیر، نمونه‌هایی از چند زاویه حاده یا تند را نمایش می‌دهد. ضلع‌های این زاویه‌ها، به یکدیگر نزدیک‌ترند. به همین دلیل، در اغلب موارد، می‌توان به سادگی زاویه‌های تند را با چشم تشخیص داد.

تصویر زیر، چند مثال از زاویه‌های تند در دنیای واقعی است. محیط اطراف خود را به دقت بررسی کنید تا ببینید می‌توانید مثال‌های دیگری از زاویه حاده پیدا کنید.

زاویه باز چیست؟

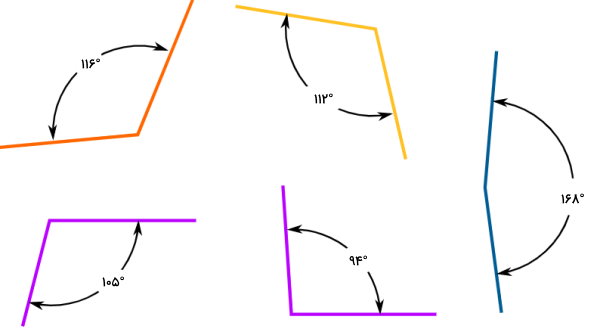
زاویه باز، در مقابل زاویه تند قرار می‌گیرد. اندازه این زاویه، بزرگتر از ۹۰ درجه است. البته زاویه‌های باز، اندازه‌ای کوچکتر از ۱۸۰ درجه دارند. این زاویه‌ها، با عنوان زاویه منفرجه نیز شناخته می‌شوند. اگر به مثال‌های زیر دقت کنید، متوجه خواهید شد که بازشدگی بین ضلع‌های زاویه منفرجه، نسبت به زاویه حاده بیشتر است. به همین دلیل است که به این زاویه، باز می‌گویند.

در بسیاری از موارد، زاویه‌های باز نیز مانند زاویه‌های تند، با چشم تشخیص داده می‌شوند. با این وجود، اگر اندازه این زاویه‌ها به ۹۰ یا ۱۸۰ درجه نزدیک باشد، بهتر است از ابزارهای هندسی نظیر گونیا و نقاله برای تشخیص بهتر آن‌ها استفاده کرد.

زاویه راست چیست؟

در تعریف زاویه‌های تند و باز، دیدیم که این زاویه‌ها با توجه به اندازه ۹۰ درجه تشخیص داده می‌شوند. یکی از مهم‌ترین و پرکاربردترین زاویه‌هایی که باید با آن آشنا شوید، زاویه راست است. این زاویه، با عنوان زاویه قائمه نیز شناخته می‌شود. اندازه زاویه قائمه دقیقا برابر با ۹۰ درجه است. تصویر زیر، مقایسه زاویه راست با دو زاویه تند و باز را نمایش می‌دهد.

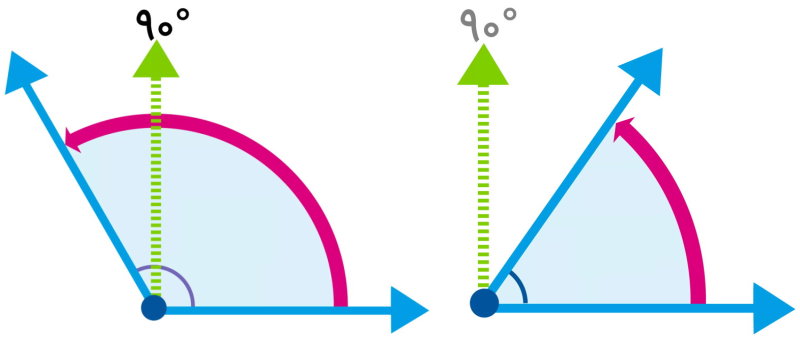
تعریف زاویه‌‌های تند و باز بر اساس زاویه راست به صورت زیر بیان می‌شود:

• زاویه تند: زاویه‌ای که از زاویه راست کوچکتر باشد، با عنوان زاویه تند شناخته می‌شود.
• زاویه باز: زاویه‌ای که از زاویه راست بزرگ‌تر باشد، با عنوان زاویه باز شناخته می‌شود.

برای نمایش زاویه‌های راست، می‌توانیم از زاویه بین عقربه‌های ساعت استفاده کنیم. به عنوان مثال، عقربه‌های ساعت در زمان‌هایی 03:00 یا 09:00 با یکدیگر زاویه راست می‌سازند.

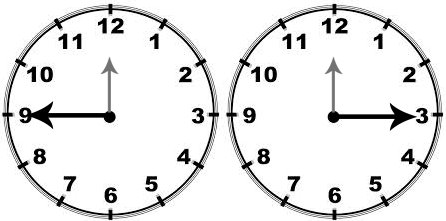
بهترین ابزار برای بررسی قائمه بودن یک زاویه، گونیا است. این وسیله، به یک مثلث قائم الزاویه شباهت دارد. با استفاده از گوشه راست و ساق‌های گونیا، می‌توان نوع برخی از زاویه‌ها مانند زاویه راست، تند و باز را تشخیص داد.

زاویه نیم صفحه چیست؟

زاویه نیم‌صفحه، همان زاویه ۱۸۰ درجه است. در نگاه اول، این زاویه به شکل یک خط دیده می‌شود. در صورتی که زاویه نیم‌صفحه نیز مانند تمام زاویه‌های دیگر، یک راس و دو ضلع دارند. ضلع‌های این زاویه، در جهت خلاف یکدیگر قرار می‌گیرند. به همین دلیل، در زاویه‌های ۱۸۰ درجه، شکلی مشابه با شکل زیر به وجود می‌آید. در برخی از موارد، به زاویه نیم‌صفحه، زاویه مستقیم می‌گویند؛ چراکه این زاویه مشابه یک خط مستقیم است.

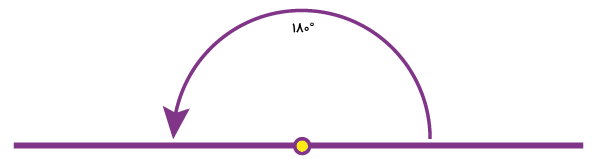
مثال‌های بسیار زیادی از زاویه نیم‌صفحه در اطراف ما وجود دارند. تصویر زیر، فقط دو نمونه از این مثال‌ها را نمایش می‌دهد. هر گاه عقربه‌های ساعت، در خلاف جهت یکدیگر قرار می‌گیرند، یک زاویه نیم‌صفحه به وجود می‌آید.

در بخش‌های قبل، اشاره کردیم که زاویه ۱۸۰ درجه، معیاری برای تشخیص زاویه باز است. این زاویه، در تشخیص زاویه کاو نیز کاربرد دارد.

زاویه کاو چیست؟

زاویه کاو، زاویه‌ای بین ۱۸۰ تا ۳۶۰ درجه است. زاویه کاو با عنوان زاویه مقعر نیز شناخته می‌شود. تصویر زیر، چندین نمونه از زاویه‌های کاو را نمایش می‌دهد. نکته مهم در زاویه‌های مقعر یا کاو، جهت اندازه‌گیری میزان بازشدگی ضلع‌های آن‌ها است.

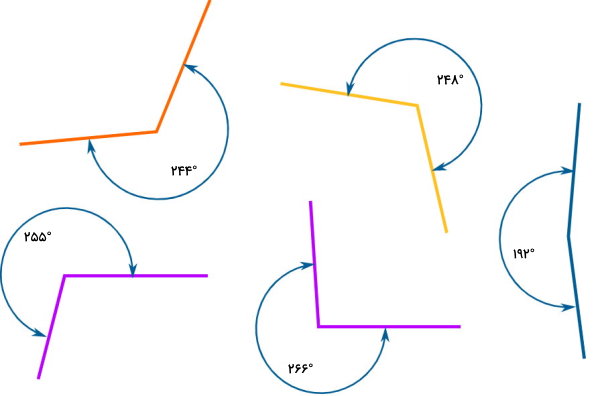
تشخیص زاویه‌های مقعر، معمولا توسط یک ابزار هندسی با عنوان نقاله انجام می‌گیرد. این وسیله، به شکل یک نیم‌دایره است. بر روی کمان نقاله، اعداد ۰ تا ۱۸۰ درجه درج شده‌اند. در زاویه‌های مقعر، موقعیت ضلع‌های زاویه و نقاله به شکل زیر در می‌آید.

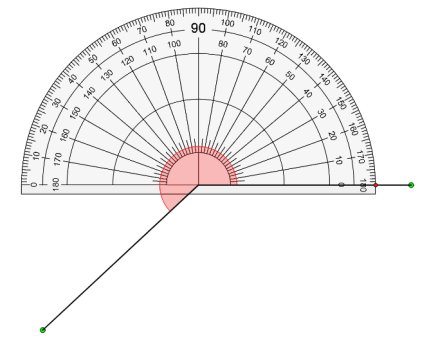
زاویه‌های کاو، همان زاویه‌های تند یا باز هستند که اندازه‌گیری آن‌ها در جهت مخالف انجام می‌شود. به عنوان مثال، زاویه نمایش داده شده در تصویر زیر را در نظر بگیرید. این زاویه، از یک سمت دارای اندازه ۳۱۲ درجه (زاویه کاو) و سمت دیگر دارای اندازه ۴۸ درجه (زاویه تند) است. در بخش‌های بعدی، بیشتر به توضیح این مسئله خواهیم پرداخت.

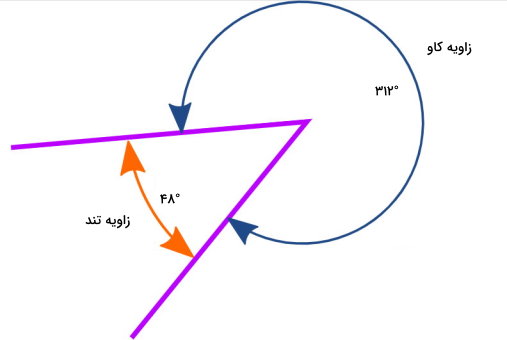
زاویه تمام صفحه چیست؟

زاویه تمام صفحه، همان زاویه ۳۶۰ درجه است. به این زاویه، زاویه کامل نیز می‌گویند. اگر یک ضلع زاویه، حول راس، به طور کامل بچرخد، زاویه ۳۶۰ درجه تشکیل می‌شود. چرخش کامل عقربه‌های ساعت، لاستیک ماشین و غیره، ازنمونه‌های واقعی ایجاد زاویه تمام‌صفحه هستند.

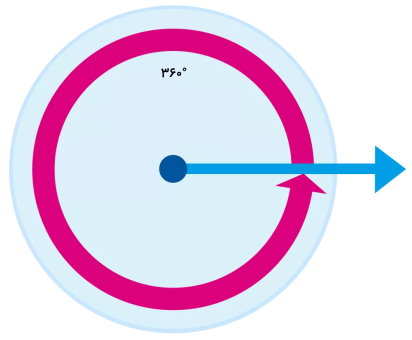
انواع زاویه بر اساس جهت اندازه گیری

معیار دوم برای دسته‌بندی زاویه‌ها، جهت اندازه‌گیری آن‌ها است. در بخش مربوط به زاویه کاو یا مقعر، اشاره کوچکی به این مسئله داشتیم. زاویه‌ها، از نظر جهت اندازه‌گیری، به دو نوع مثبت و منفی تقسیم می‌شوند. پیش از تعریف این زاویه‌ها، شما را با نحوه اندازه‌گیری آن‌ها آشنا می‌کنیم.

اندازه گیری انواع زاویه ها

اندازه‌گیری زاویه‌ها، با استفاده از نقاله انجام می‌گیرد. این وسیله، امکان تعیین نسبتا دقیق اندازه زاویه و تشخیص نوع آن (بر اساس مقدار به دست آمده) را فراهم می‌کند. اجزای مختلف نقاله، در تصویر زیر نمایش داده شده‌اند.

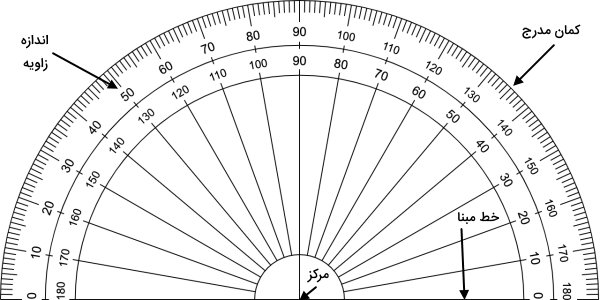
خط مبنای نقاله، ضلع یک زاویه نیم‌صفحه (۱۸۰) درجه است. مرکز نقاله نیز به عنوان راس این زاویه در نظر گرفته می‌شود. بنابراین، اگر مرکز و خط مبنای نقاله را با راس و یکی از ضلع‌های زاویه تنظیم کنیم، اندازه آن زاویه به کمک اعداد روی کمان مدرج به دست می‌آید. نکته مهم در فرآیند اندازه‌گیری زاویه، جهت خواندن اعداد است.

بر روی کمان نقاله، دو سری عدد وجود دارد. یک سری از این اعداد، در جهت پادساعتگرد افزایش می‌یابند (عدد ۰ در سمت راست قرار دارد). اعداد سری دیگر، ساعتگرد هستند (عدد ۰ در سمت چپ قرار دارد). برای حالت اول، سمت راست خط مبنای نقاله را به صورت زیر بر روی یکی از ضلع‌های زاویه تنظیم می‌کنیم. توجه داشته باشید که مرکز نقاله باید بر روی راس زاویه قرار بگیرید.

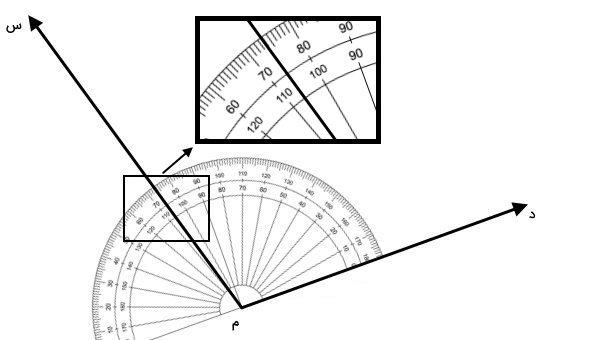
شمارش اعداد را از عدد ۰ در سمت راست نقاله شروع می‌کنیم. با رسیدن به محل برخورد ضلع دیگر زاویه و کمان نقاله، شمارش را متوقف می‌کنیم. عدد نمایش داده شده برابر با 106 درجه است. برای حالت دوم، سمت چپ خط مبنای نقاله را با ضلع دیگر زاویه تنظیم می‌کنیم.

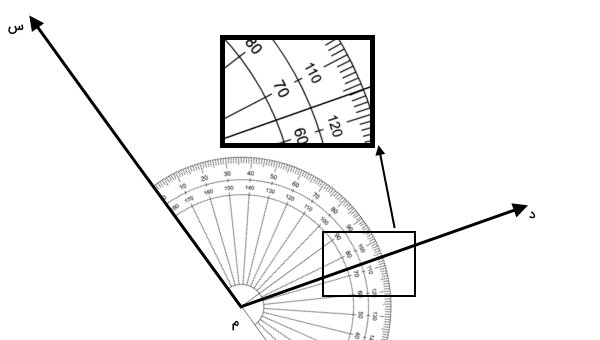
این بار نیز، اعداد روی کمان را از عدد ۰ (در سمت چپ) می‌شماریم. ضلع دیگر زاویه، مجدد در زاویه 106 درجه، کمان نقاله را قطع می‌کند. در هر دو حالت، مقدار به دست آمده برای زاویه‌ها، یکسان است. با این وجود، نوع هر زاویه از نظر جهت اندازه‌گیری، با یکدیگر تفاوت دارد. زاویه اول، برابر با 106 درجه مثبت و زاویه دوم برابر با 106 درجه منفی است.

زاویه مثبت چیست؟

به زاویه‌ای که در جهت خلاف حرکت عقربه‌های ساعت (پادساعتگرد) اندازه‌گیری شود، زاویه مثبت می‌گویند. جهت ایجاد زاویه بر روی مثبت بودن آن تاثیر دارد. به عنوان مثال، ضلع مبدا در شکل زیر را در نظر بگیرید.

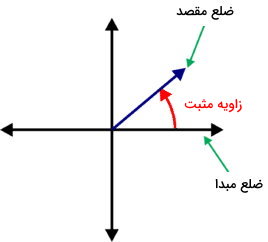
اگر ضلع مبدا، در جهت خلاف عقربه‌های ساعت حرکت کرده و در موقعیت ضلع مقصد توقف کند، یک زاویه مثبت به وجود می‌آید. این زاویه و جهت اندازه‌گیری آن با رنگ قرمز مشخص شده است.

زاویه منفی چیست؟

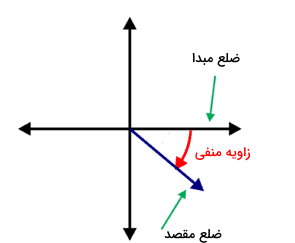
به زاویه‌ای که در جهت حرکت عقربه‌های ساعت (ساعتگرد) اندازه‌گیری شود، زاویه منفی می‌گویند. در تصویر زیر، ضلع مبدا و ضلع مقصد نمایش داده شده است. فلش قرمز رنگ، مسیر حرکت ضلع مبدا تا رسیدن به ضلع مقصد را نمایش می‌دهد. به دلیل، حرکت در جهت عقربه‌های ساعت، زاویه ایجاد شده از نوع منفی است.

انواع جفت زاویه

زاویه متمم، مکمل، جفت خطی، مجاور و متقابل به راس، از انواع جفت زاویه‌ها هستند. بین اندازه این زاویه‌ها، یک رابطه وجود دارد. در ادامه، به معرفی هر یک از انواع جفت زاویه می‌پردازیم.

زاویه مجاور چیست ؟

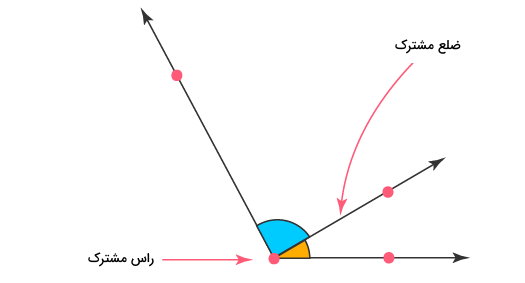
«زاویه‌های مجاور» (Adjacent Angle)، زاویه‌هایی هستند که یک ضلع و راس مشترک دارند. دو زاویه مجزا، یا دو زاویه‌ای که بخشی از آن‌ها بر روی هم قرار بگیرد، زاویه‌های مجاور محسوب نمی‌شوند. تصویر زیر، مفهوم درست و نادرست زاویه‌های مجاور را نمایش می‌دهد.

زاویه متمم چیست؟

به هر دو زاویه‌ای که مجموع آن‌ها برابر با ۹۰ درجه باشد، «زاویه‌های متمم» (Complementary Angles) می‌گویند. به عنوان مثال، در تصویر زیر، زاویه‌های ۳۰ و ۶۰ درجه، یک زاویه راست می‌سازند. بنابراین، این دو زاویه، متمم یکدیگر هستند.

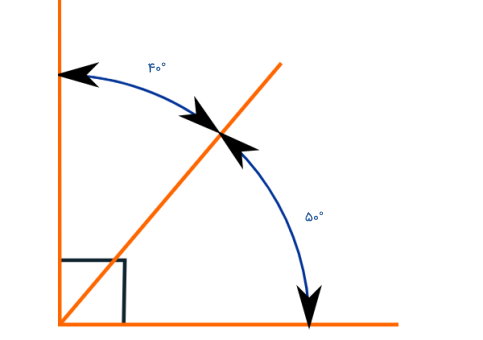
به منظور متمم بودن دو زاویه، نیازی به وجود ضلع و راس مشترک (مجاور بودن دو زاویه) نیست. زاویه‌های متمم می‌تواند دو زاویه غیر مجاور در یک چندضلعی یا حتی دو زاویه جدا از هم باشند. به عنوان مثال، تصویر زیر، دو زاویه متمم جدا از هم را نمایش می‌دهد.

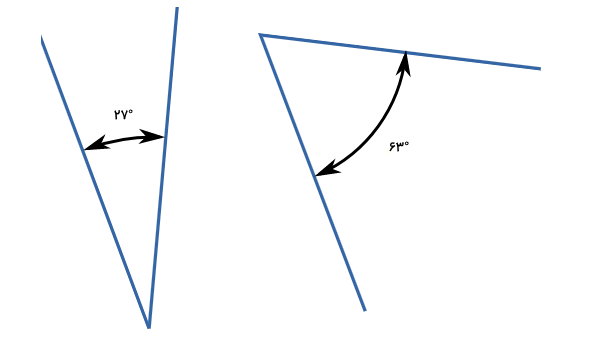
زاویه مکمل چیست؟

به هر دو زاویه‌ای که مجموع آن‌ها برابر با ۱۸۰ درجه باشد، «زاویه‌های مکمل» (Supplementary Angles) می‌گویند. به عنوان مثال، از کنار هم قرار دادن دو زاویه راست، یک زاویه مستقیم به وجود می‌آید. بنابراین، زاویه‌های راست، مکمل یکدیگرند. زاویه‌های مکمل نیز مانند زاویه‌های متمم، می‌توانند دارای ضلع و راس مشترک یا جدا از هم باشند. تصویر زیر، نمونه‌هایی از چند زاویه متمم را نمایش می‌دهد.

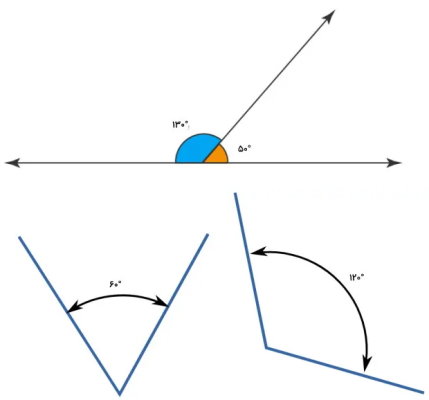
زاویه متقابل به راس چیست؟

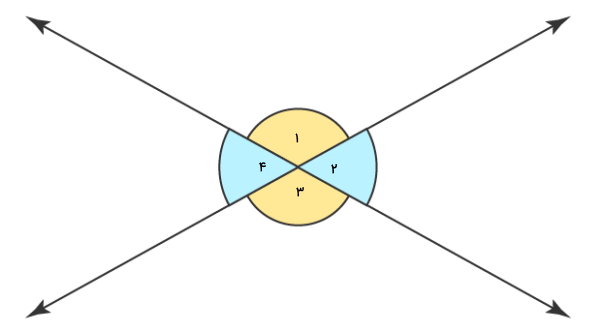
هنگامی که دو خط همدیگر را قطع می‌کنند، چهار زاویه در محل برخوردشان به وجود می‌آید. این زاویه‌ها، دو به دو در مقابل هم قرار می‌گیرند و با عنوان «زاویه‌های متقابل به راس» (Vertical Angles) شناخته می‌شوند. زاویه‌های متقابل به راس، هم‌اندازه‌اند.

جفت زاویه های خطی چیست؟

«جفت زاویه‌های خطی» (Linear Pair of Angles)، زاویه‌هایی هستند که از تقاطع دو خط در یک نقطه به وجود می‌آیند. دلیل وجود عبارت «خطی» در عنوان این زاویه‌ها، تشکیل یک زاویه نیم‌صفحه توسط هر دو زاویه مجاور است. به عبارت دیگر، جفت زاویه‌های خطی، مکمل یکدیگرند.

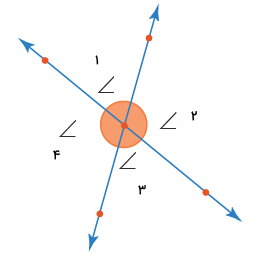
جفت زاویه‌های خطی در تصویر بالا عبارت هستند از:

• زاویه 1 و 2
• زاویه 2 و 3
• زاویه 3 و 4
• زاویه 4 و 1

زاویه های متقاطع و انواع آن‌ها

«زاویه‌های متقاطع» (Transversal Angles)، زاویه‌هایی هستند که از برخورد یک خط با دو خط دیگر ایجاد می‌شوند. در تصویر زیر، خط A، دو خط B و C را قطع می‌کند. به این ترتیب، زاویه‌های ۱ تا ۸ به وجود می‌آیند.

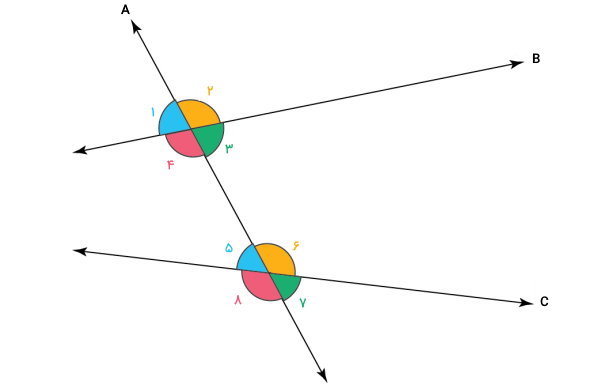
زاویه‌هایی که در شکل بالا ایجاد شده‌اند، عبارت هستند از:

• زاویه های متناظر
• زاویه های متبادل داخلی
• زاویه های مجاور داخلی
• زاویه های متبادل خارجی
• زاویه های متقابل به راس

راجع به زاویه‌های متقابل به راس، در بخش قبلی صحبت کردیم. در ادامه، انواع دیگر زاویه‌های متقاطع را مورد بررسی قرار می‌دهیم.

زاویه متناظر

«زاوی‌های متناظر» (Corresponding Angles)، جفت زاویه‌هایی هستند که در خط‌های متقاطع، از نظر موقعیت قرارگیری، به یکدیگر شباهت دارند. زاویه‌های ۲ و ۶ در تصویر زیر، دو نمونه از زاویه‌های متناظر هستند.

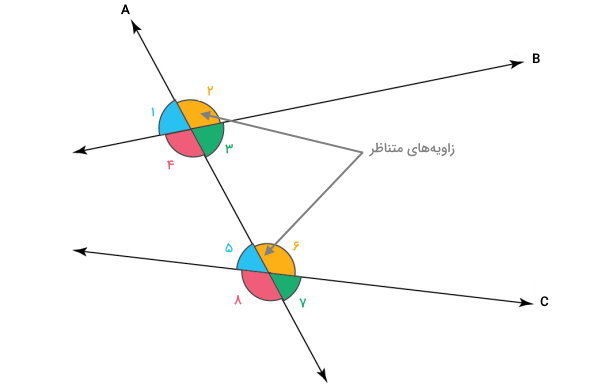
زاویه متبادل داخلی

چهار زاویه از هشت زاویه ایجاد شده از تقاطع خط‌ها، در فاصله بین دو خط غیرمتقاطع قرار می‌گیرند. به این زاویه‌ها، زاویه‌های متقاطع داخلی می‌گویند. در تصویر زیر، چهار زاویه ۳، ۴، ۵ و ۶، زاویه‌های داخلی هستند. از بین این موارد، زاویه‌هایی که در طرف مقابل هم قرار می‌گیرند، با عنوان زاویه‌های متبادل داخلی شناخته می‌شوند.

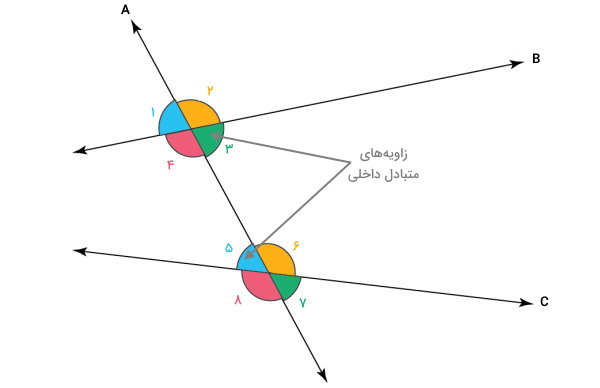
زاویه مجاور داخلی

به زاویه‌های متقاطع داخلی با یک ضلع مشترک، زاویه مجاور داخلی می‌گویند. زاویه‌های ۳ و ۶ و زاویه‌های ۴ و ۵، زاویه‌های مجاور داخلی محسوب می‌شوند.

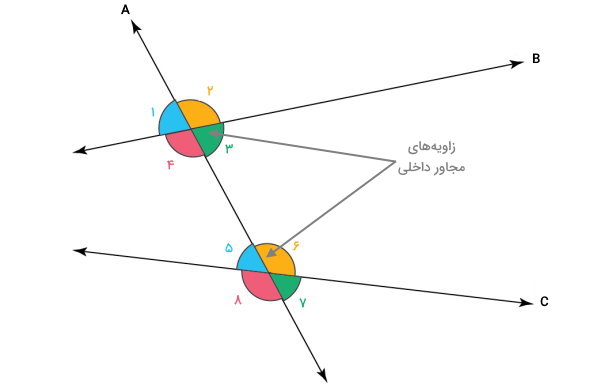
زاویه متبادل خارجی

چهار زاویه‌ای که در محدوده خارج از فاصله بین دو خط غیرمتقاطع قرار دارند، با عنوان زاویه‌های متقاطع خارجی شناخته می‌شوند. در تصویر زیر، زاویه‌های ۱، ۲، ۷ و ۸، زاویه‌های متقاطع خارجی هستند. به زاویه‌های متقاطع خارجی مخالف یکدیگر، زاویه‌های متبادل خارجی می‌گویند.

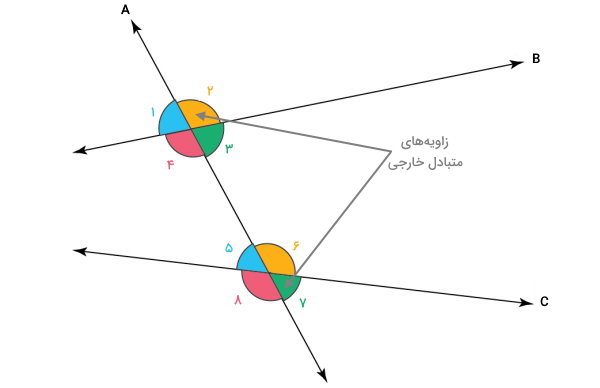
انواع زاویه در چند ضلعی ها

چندضلعی‌ها، شکل‌هایی هستند که از یک خط بسته شکسته تشکیل می‌شوند. از مهم‌ترین اجزای چندضلعی‌ها می‌توان به ضلع، راس، زاویه داخلی و زاویه خارجی اشاره کرد.

تصویر زیر، دیگر اجزای یک چندضلعی را نمایش می‌دهد.

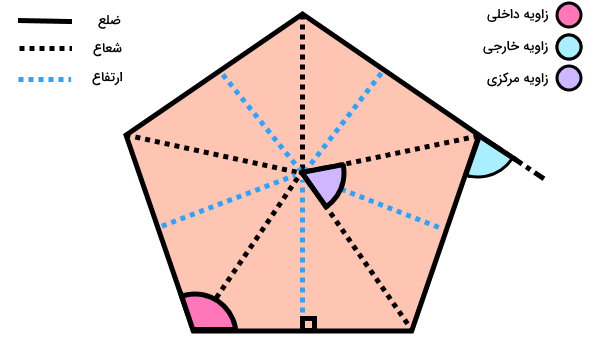
زاویه‌ها، بخصوص زاویه داخلی، از اجزای مهم چندضلعی‌ها به شمار می‌روند. یکی از معیارهای دسته‌بندی انواع چندضلعی‌ها (محدب، مقعر، منتظم، غیرمنتظم و غیره)، زاویه داخلی آن‌ها است. در ادامه، هر یک از انواع زاویه در چندضلعی‌ها معرفی می‌کنیم.

زاویه داخلی در چند ضلعی ها

ضلع‌های چندضلعی، یکدیگر را در نقطه‌ای به نام راس قطع می‌کنند. به همین دلیل، در محدوده راس‌های چندضلعی، یک زاویه به وجود می‌آید. این زاویه با عنوان زاویه داخلی شناخته می‌شود.

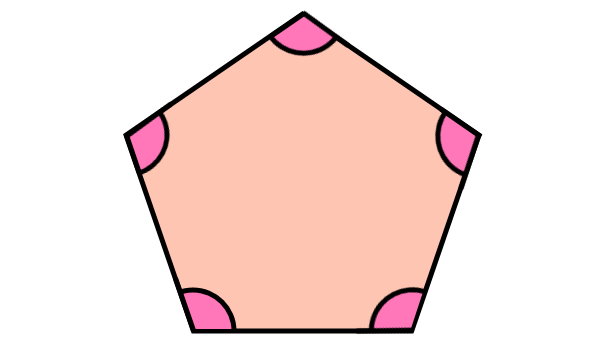
زاویه‌های مجاور داخلی

در چندضلعی‌ها، به هر دو زاویه داخلی که یک ضلع مشترک داشته باشند، زاویه مجاور داخلی می‌گویند.

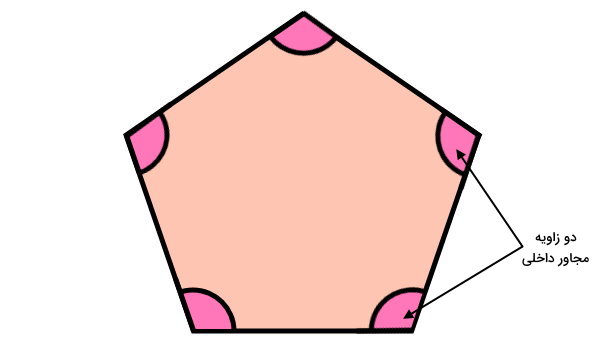
مباحث گسترده‌ای در مورد زوایای داخلی چندضلعی‌ها وجود دارند که توضیح آن‌ها از هدف این آموزش خارج است. در صورت علاقه به یادگیری در مورد این مباحث، مطالعه مطالب زیر را به شما پیشنهاد می‌کنیم:

• زاویه داخلی و تعریف آن در هندسه — به زبان ساده
• زاویه داخلی و محاسبات آن در اشکال چندضلعی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
• فرمول بدست آوردن مجموع زوایای داخلی چند ضلعی + حل تمرین
• مجموع زوایای داخلی مثلث چند درجه است؟ + اثبات و مثال به زبان ساده
• مجموع زوایای داخلی ذوزنقه چقدر است؟ + حل تمرین و مثال
• مجموع زوایای داخلی پنج‌ضلعی چند درجه است؟ — به زبان ساده
• مجموع زوایای داخلی هشت‌ضلعی و هشت‌ضلعی منتظم — با مثال
• مجموع زوایای داخلی چندضلعی محدب چیست؟ — به زبان ساده + حل مثال
• مجموع زوایای چندضلعی مقعر — به زبان ساده + حل تمرین و اثبات فرمول

زاویه خارجی در چند ضلعی ها

با امتداد دادن ضلع‌ها، زاویه‌ای بین ضلع مجاور و امتداد به وجود می‌آید. این زاویه با عنوان زاویه خارجی شناخته می‌شود. زاویه داخلی و خارجی یک راس، با یکدیگر زاویه ۱۸۰ درجه می‌سازند. بنابراین، بر اساس تعاریف در بخش‌های قبلی، این دو زاویه، مکمل هستند.

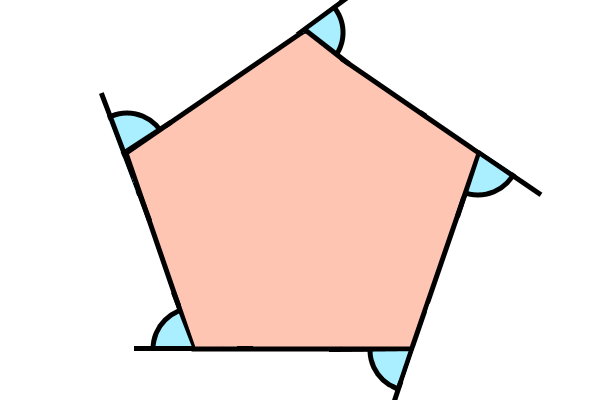
در صورت تمایل به یادگیری بیشتر راجع به زوایای خارجی چندضلعی‌ها، مطالعه مطالب زیر را به شما پیشنهاد می‌کنیم:

• زاویه خارجی در چندضلعی‌ها — به زبان ساده (+ دانلود فیلم آموزش رایگان)
• مجموع زوایای خارجی چندضلعی منتظم — به زبان ساده + اثبات
• مجموع زوایای خارجی چندضلعی محدب چیست؟ — به زبان ساده + حل مثال

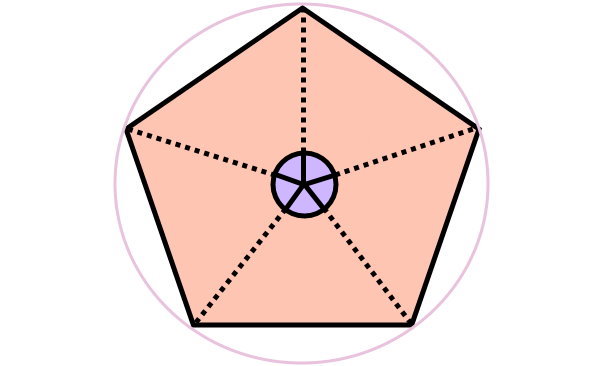
زاویه مرکزی در چند ضلعی ها

یکی دیگر از انواع زاویه‌ها در چندضلعی‌ها، زاویه مرکزی است. این زاویه، به اندازه زاویه‌های داخلی و خارجی شناخته شده نیست. اگر مرکز چندضلعی را به گوشه‌های آن وصل کنیم، پاره‌خطی به وجود می‌آید که با عنوان شعاع چندضلعی شناخته می‌شود. شعاع‌های چندضلعی در مرکز آن، زاویه‌ای به نام زاویه مرکزی را تشکیل می‌دهند.

انواع زاویه در مثلث ها

زاویه قائمه، از اهمیت بالایی در مثلث‌ها برخوردار است. اگر مثلثی، دارای یک زاویه ۹۰ درجه باشد، به آن مثلث قائم الزاویه یا مثلث راست گوشه می‌گویند.

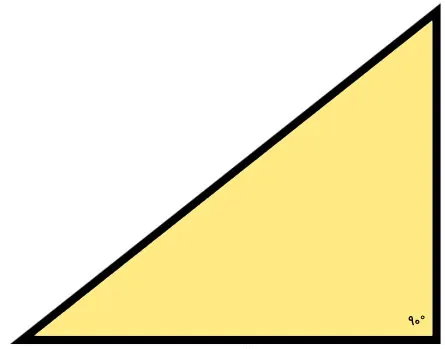
مثلث‌ها می‌توانند حداکثر سه زاویه حاده، حداکثر یک زاویه قائمه و حداکثر یک زاویه منفرجه داشته باشند. نوع زاویه‌های این شکل هندسی، یکی از مهم‌ترین معیارهای تقسیم‌بندی انواع آن (مثلث حاده، مثلث منفرجه و مثلث قائم الزاویه) است.

زاویه متمم در مثلث ها

تمام مثلث‌های قائم الزاویه، دارای دو زاویه متمم هستند. مجموع زوایای داخلی هر مثلث، برابر با ۱۸۰ درجه می‌شود. از طرفی، مثلث قائم الزاویه، همواره یک زاویه راست یا ۹۰ درجه دارد. به این ترتیب، می‌توانیم رابطه زیر را برای زاویه‌های یک مثلث قائم الزاویه بنویسیم:

۱۸۰° = زاویه سوم + زاویه دوم + زاویه قائمه

۱۸۰° = زاویه سوم + زاویه دوم + °۹۰

 ۹۰° - ۱۸۰° = زاویه سوم + زاویه دوم

 ۹۰° = زاویه سوم + زاویه دوم

در نتیجه، دو زاویه مثلث قائم الزاویه، متمم یکدیگرند.

انواع زاویه در دایره

دایره، شکلی است که از یک منحنی بسته با زاویه ۳۶۰ درجه تشکیل می‌شود. زاویه‌های مختلفی را می‌توان برای یک دایره تعریف کرد. زاویه مرکزی، محاطی، محیط، داخلی و خارجی، نمونه‌هایی از انواع زاویه در دایره هستند.

این زاویه‌ها، بر اساس موقعیت قرارگیری ضلع‌هایشان نسبت به اجزای دایره تشخیص داده می‌شود. از این‌رو، بهتر است ابتدا با نگاه کردن به تصویر زیر، با برخی از اجزای اصلی دایره آشنا شوید.

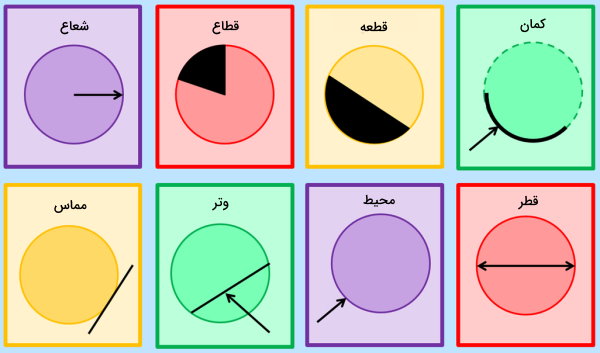
زاویه مرکزی در دایره

زاویه مرکزی دایره، زاویه بین دو شعاع آن است. در این نوع زاویه، مرکز دایره به عنوان راس زاویه و شعاع‌های دایره، به عنوان ضلع‌های زاویه در نظر گرفته می‌شوند. اندازه زاویه مرکزی دایره، با اندازه کمان رو به روی آن برابر است.

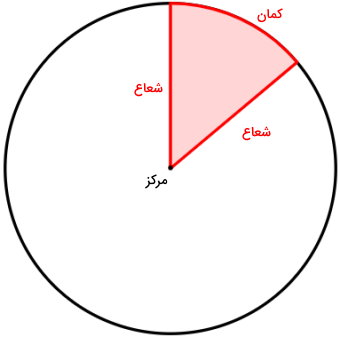
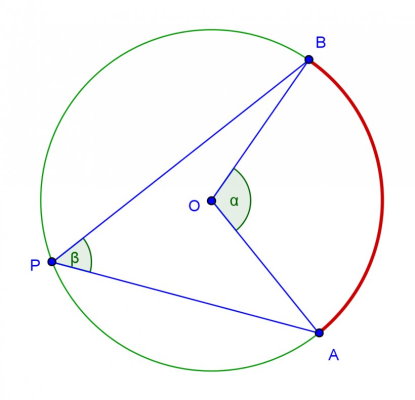
زاویه محاطی در دایره

به زاویه‌ای که راس آن بر روی محیط دایره قرار داشته باشد و ضلع‌های آن از وترهای دایره تشکیل شوند، زاویه محاطی می‌گویند. اندازه زاویه محاطی مقابل به یک کمان، برابر با نصف اندازه زاویه مرکزی مقابل به همان کمان است.

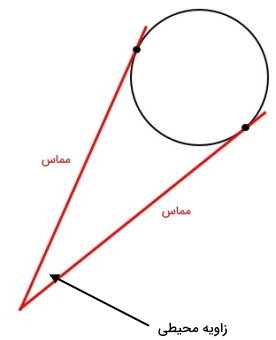
زاویه محیطی در دایره

به زاویه‌ای که از برخورد دو مماس دایره تشکیل می‌شود، زاویه محیطی می‌گویند.

زاویه داخلی در دایره

زاویه داخلی دایره، زاویه‌ای است که ضلع‌ها و راس آن درون دایره قرار می‌گیرند. در تصویر زیر، هر چهار زاویه ۱ تا ۴، به عنوان زاویه‌های داخلی در نظر گرفته می‌شوند.

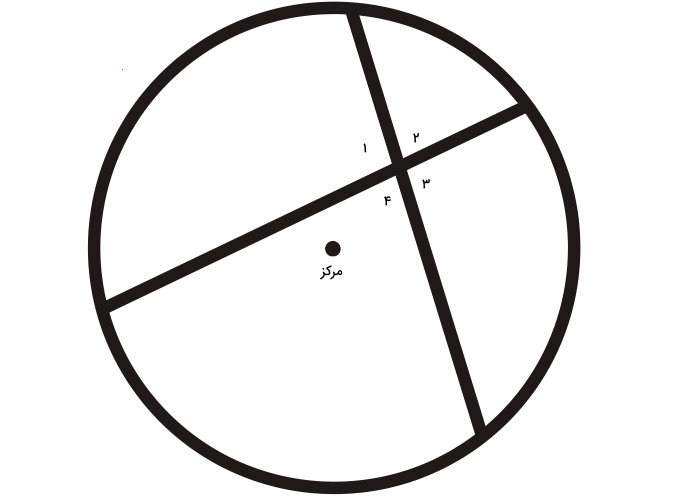
زاویه خارجی دایره

به زاویه‌ای که راس آن، خارج از دایره قرار گرفته باشد و هر ضلع آن، دایره را در دو نقطه قطع کند، زاویه خارجی دایره می‌گویند.

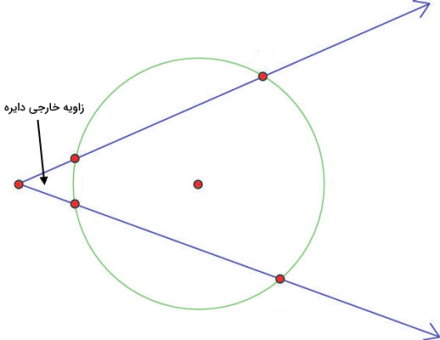
زاویه نیم صفحه در دایره و نیم دایره

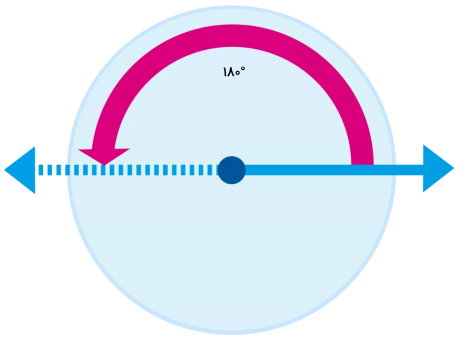
یکی از زوایای متداول در دایره‌ها، زاویه نیم‌صفحه است. این زاویه، با رسم قطرهای دایره به وجود می‌آید. در واقع، هر قطر، دایره را به دو نیم‌دایره با زاویه ۱۸۰ درجه تقسیم می‌کند.

سوالات مرتبط با انواع زاویه ها

در این بخش، به برخی از سوالات پرتکرار در رابطه با انواع زاویه به طور خلاصه پاسخ می‌دهیم.

انواع زاویه را نام ببرید ؟

زاویه صفر، زاویه تند (حاده)، زاویه راست (قائمه)، زاویه باز (منفرجه)، زاویه خط راست (نیم‌صفحه)، زاویه کاو (مقعر) و زاویه کامل (تمام صفحه)، از انواع زاویه‌ها هستند.

انواع زاویه چند درجه است ؟

زاویه‌ها از نظر نوع برابر با ۰ درجه، ۰ تا ۹۰ درجه، ۹۰ درجه، بین ۹۰ تا ۱۸۰ درجه، ۱۸۰ درجه، بین ۱۸۰ تا ۳۶۰ درجه و ۳۶۰ درجه هستند.

نام زاویه های مثلث چیست ؟

نام زاویه‌های مختلف در انواع مثلث، عبارت از زاویه حاده، زاویه قائمه و زاویه منفرجه است.

انواع زاویه چند ضلعی چه هستند؟

زاویه‌های داخلی، خارجی و مرکزی، از انواع زاویه در چندضلعی‌ها هستند.

نام زاویه 180 درجه چیست ؟

زاویه نیم‌صفحه.

به زاویه کمتر از 270 درجه و بیشتر از 180 درجه چه می گویند ؟

زاویه بازتاب، زاویه کاو یا زاویه مقعر.

نام زاویه 360 درجه چیست ؟

زاویه تمام صفحه.