در ادامه مجموعه آموزشهای ریاضیات مجله فرادرس، در این آموزش به مبحث انحنا و شعاع انحنا میپردازیم. در ادامه، ابتدا انحنا را تعریف میکنیم، سپس نحوه به دست آوردن شعاع انحنا را بیان خواهیم کرد.
تعریف انحنا و شعاع انحنا
یک منحنی مسطح را در نظر بگیرید که با معادله y = f ( x ) y = f (x) y = f ( x ) خط مماس بر منحنی در نقطه M ( x , y ) M(x , y ) M ( x , y )
خط مماس، زاویه α \alpha α
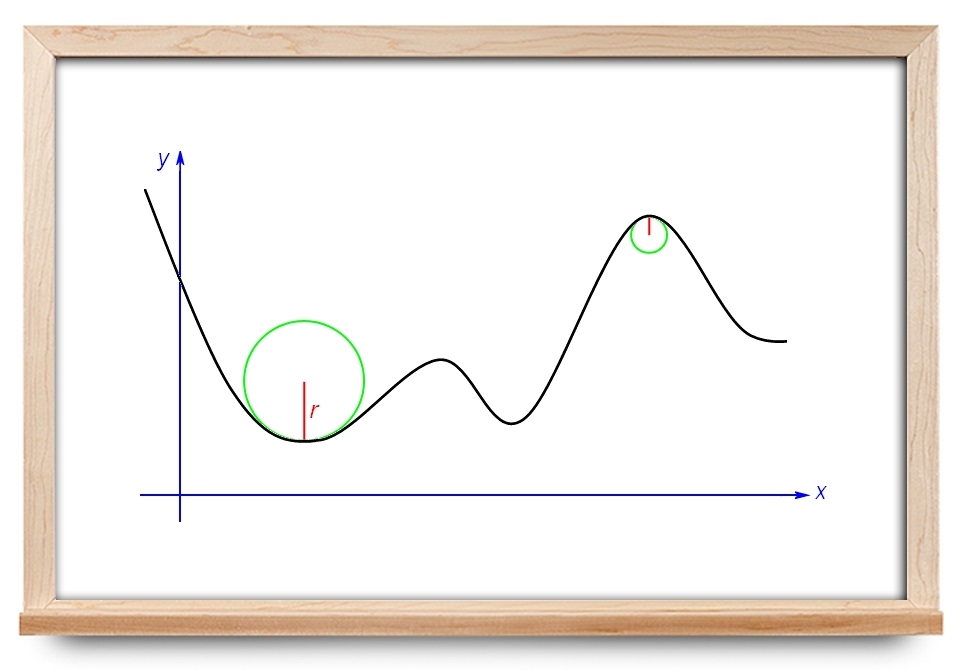
شکل ۱ با جابجایی Δ s \Delta s Δ s M M M M 1 M_1 M 1 M 1 M_1 M 1 x x x α + Δ α \alpha + \Delta\alpha α + Δ α Δ s \Delta s Δ s Δ α \Delta \alpha Δ α α \alpha α
قدر مطلق نسبت Δ α Δ s \large\frac{{\Delta \alpha }}{{\Delta s}}\normalsize Δ s Δ α M M 1 MM_1 M M 1 Δ s → 0 \Delta s \to 0 Δ s → 0 M M M
K = lim Δ s → 0 ∣ Δ α Δ s ∣ . \large K = \lim \limits _ { \Delta s \to 0 } \left | { \frac { { \Delta \alpha } } { { \Delta s } } } \right | . K = Δ s → 0 lim Δ s Δ α .
با توجه به تعریف بالا، انحنای منحنی در یک نقطه، سرعت چرخش خط مماس بر منحنی را در این نقطه نشان میدهد.
برای یک منحنی مسطح با معادله y = f ( x ) y = f (x) y = f ( x ) M ( x , y ) M(x , y ) M ( x , y ) مشتقهای اول و دوم تابع f ( x ) f (x) f ( x )
K = ∣ y ′ ′ ( x ) ∣ [ 1 + ( y ’ ( x ) ) 2 ] 3 2 . \large K = \frac { { \left | { y ^ { \prime \prime } \left ( x \right ) } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ \left ( x \right ) } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . K = [ 1 + ( y ’ ( x ) ) 2 ] 2 3 y ′′ ( x ) .
اگر منحنی به فرم پارامتری و با معادلات x = x ( t ) x = x (t) x = x ( t ) y = y ( t ) y = y (t) y = y ( t ) M ( x , y ) M(x , y ) M ( x , y )
K = ∣ x ’ y ′ ′ – y ’ x ′ ′ ∣ [ ( x ’ ) 2 + ( y ’ ) 2 ] 3 2 . \large K = \frac { { \left | { x ’ y ^ { \prime \prime } – y ’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x ’ } \right ) } ^ 2 } + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . K = [ ( x ’ ) 2 + ( y ’ ) 2 ] 2 3 x ’ y ′′ – y ’ x ′′ .
اگر منحنی در مختصات قطبی و با معادله r = r ( θ ) r = r\left( \theta \right) r = r ( θ )
K = ∣ r 2 + 2 ( r ’ ) 2 – r r ′ ′ ∣ [ r 2 + ( r ’ ) 2 ] 3 2 . \large K = \frac { { \left | { { r ^ 2 } + 2 { { \left ( { r ’ } \right ) } ^ 2 } – r r ^ { \prime \prime } } \right | } } { { { { \left [ { { r ^ 2 } + { { \left ( { r ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . K = [ r 2 + ( r ’ ) 2 ] 2 3 r 2 + 2 ( r ’ ) 2 – r r ′′ .
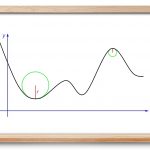
شعاع انحنای یک منحنی در نقطه M ( x , y ) M(x,y) M ( x , y ) K K K
R = 1 K . \large R = \frac { 1 } { K } . R = K 1 .
بنابراین، برای منحنیهای مسطحی که با معادله صریح y = f ( x ) y = f (x) y = f ( x ) M ( x , y ) M(x,y ) M ( x , y )
R = [ 1 + ( y ’ ( x ) ) 2 ] 3 2 ∣ y ′ ′ ( x ) ∣ . \large R = \frac { { { { \left [ { 1 + { { \left ( { y ’ \left ( x \right ) } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } \left ( x \right ) } \right | } } . R = ∣ y ′′ ( x ) ∣ [ 1 + ( y ’ ( x ) ) 2 ] 2 3 .
مثالها
در این بخش، چند مثال را بیان میکنیم.
مثال ۱
انحنا و رئوس بیضی زیر را محاسبه کنید.
x 2 a 2 + y 2 b 2 = 1 \large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 a 2 x 2 + b 2 y 2 = 1
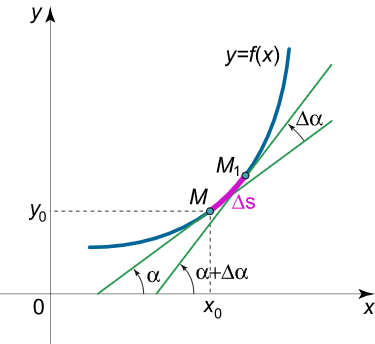
حل: کافی است انحنا را در نقاط A ( a , 0 ) A (a , 0 ) A ( a , 0 ) B ( 0 , b ) B(0,b) B ( 0 , b )
شکل ۲ برای محاسبه انحنا، نوشتن فرم پارامتری بیضی محاسبات را سادهتر خواهد کرد:
x = a cos t , y = b sin t \large x = a \cos t , \; \; \; y = b \sin t x = a cos t , y = b sin t
که در آن، t t t A ( a , 0 ) A (a,0) A ( a , 0 ) t = 0 t =0 t = 0 B ( 0 , b ) B( 0 , b ) B ( 0 , b ) t = π 2 t = \large\frac{\pi }{2}\normalsize t = 2 π
مشتق اول و دوم معادلات به صورت زیر است:
x ’ = x ’ t = ( a cos t ) ′ = – a sin t , x ′ ′ = x t t ′ ′ = ( – a sin t ) ′ = – a cos t ; y ’ = y ’ t = ( b sin t ) ′ = b cos t , x ′ ′ = x t t ′ ′ = ( b cos t ) ′ = – b sin t . \large \begin {align*} x ’ & = { x ’ _ t } = { \left ( { a \cos t } \right ) ^ \prime } = – a \sin t , \; \; \; \kern-0.3pt \\ x ^ { \prime \prime } & = { x ^ { \prime \prime } _ { t t } } = { \left ( { – a \sin t } \right ) ^ \prime } = { – a \cos t ; } \\ y ’ & = { y ’ _ t } = { \left ( { b \sin t } \right ) ^ \prime } = b \cos t , \; \; \; \kern-0.3pt \\ x ^ { \prime \prime } & = { x ^ { \prime \prime } _ { t t } } = { \left ( { b \cos t } \right ) ^ \prime } = – b \sin t . \end {align*} x ’ x ′′ y ’ x ′′ = x ’ t = ( a cos t ) ′ = – a sin t , = x tt ′′ = ( – a sin t ) ′ = – a cos t ; = y ’ t = ( b sin t ) ′ = b cos t , = x tt ′′ = ( b cos t ) ′ = – b sin t .
انحنای یک منحنی که با فرم پارامتری توصیف شده، به صورت زیر است:
K = ∣ x ’ y ′ ′ – y ’ x ′ ′ ∣ [ ( x ’ ) 2 + ( y ’ ) 2 ] 3 2 . \large K = \frac { { \left | { x ’ y ^ { \prime \prime } – y ’ x ^ { \prime \prime } } \right | } } { { { { \left [ { { { \left ( { x ’ } \right ) } ^ 2 } + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . K = [ ( x ’ ) 2 + ( y ’ ) 2 ] 2 3 x ’ y ′′ – y ’ x ′′ .
با جایگذاری مشتقها در رابطه اخیر، داریم:
K = ∣ a b sin 2 t + a b cos 2 t ∣ ( a 2 sin 2 t + b 2 cos 2 t ) 3 2 = ∣ a b ( sin 2 t + cos 2 t ) ∣ ( a 2 sin 2 t + b 2 cos 2 t ) 3 2 = a b ( a 2 sin 2 t + b 2 cos 2 t ) 3 2 . \large \begin {align*} K & = { \frac { { \left | { a b \, { { \sin } ^ 2 } t + a b \, { { \cos } ^ 2 } t } \right | } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { \left | { a b \left ( { { { \sin } ^ 2 } t + { { \cos } ^ 2 } t } \right ) } \right | } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } \right ) } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } } \\ & = { \frac { { a b } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } t + { b ^ 2 } { { \cos } ^ 2 } t } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } \end {align*} K = ( a 2 sin 2 t + b 2 cos 2 t ) 2 3 ab sin 2 t + ab cos 2 t = ( a 2 sin 2 t + b 2 cos 2 t ) 2 3 ab ( sin 2 t + cos 2 t ) = ( a 2 sin 2 t + b 2 cos 2 t ) 2 3 ab .
اکنون مقادیر انحنا را در رئوس A ( a , 0 ) A (a , 0 ) A ( a , 0 ) B ( 0 , b ) B (0 , b ) B ( 0 , b )
K ( A ) = K ( t = 0 ) = a b ( a 2 sin 2 0 + b 2 cos 2 0 ) 3 2 = a b ( b 2 ) 3 2 = a b b 3 = a b 2 ; K ( B ) = K ( t = π 2 ) = a b ( a 2 sin 2 π 2 + b 2 cos 2 π 2 ) 3 2 = a b ( a 2 ) 3 2 = a b a 3 = b a 2 . \large \begin {align*} K \left ( A \right ) & = K \left ( { t = 0 } \right ) = { \frac { { a b } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } 0 + { b ^ 2 } { { \cos } ^ 2 } 0 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { { \left ( { { b ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { b ^ 3 } } } } = { \frac { a }{ { { b ^ 2 } } } ; } \\ K \left ( B \right ) & = K \left ( { t = \frac { \pi } { 2 } } \right ) = { \frac { { a b } } { { { { \left ( { { a ^ 2 } { { \sin } ^ 2 } \frac { \pi } { 2 } + { b ^ 2 } { { \cos } ^ 2 } \frac { \pi } { 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { { \left ( { { a ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { a b } } { { { a ^ 3 } } } } = { \frac { b } { { { a ^ 2 } } } . } \end {align*} K ( A ) K ( B ) = K ( t = 0 ) = ( a 2 sin 2 0 + b 2 cos 2 0 ) 2 3 ab = ( b 2 ) 2 3 ab = b 3 ab = b 2 a ; = K ( t = 2 π ) = ( a 2 sin 2 2 π + b 2 cos 2 2 π ) 2 3 ab = ( a 2 ) 2 3 ab = a 3 ab = a 2 b .
مثال ۲
انحنا و شعاع انحنای سهمی y = x 2 y = x ^ 2 y = x 2
حل: ابتدا مشتقات تابع را به صورت زیر مینویسیم:
y ’ = ( x 2 ) ′ = 2 x ; y ′ ′ = ( 2 x ) ′ = 2. \large { y ’ = { \left ( { { x ^ 2 } } \right ) ^ \prime } = 2 x ; } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { 2 x } \right ) ^ \prime } = 2 .} y ’ = ( x 2 ) ′ = 2 x ; y ′′ = ( 2 x ) ′ = 2.
انحنای سهمی با فرمول زیر محاسبه میشود:
K = y ′ ′ [ 1 + ( y ’ ) 2 ] 3 2 = 2 [ 1 + ( 2 x ) 2 ] 3 2 = 2 ( 1 + 4 x 2 ) 3 2 . \large { K = \frac { { y ^ { \prime \prime } } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 2 } { { { { \left [ { 1 + { { \left ( { 2 x } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 2 } { { { { \left ( { 1 + 4 { x ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } K = [ 1 + ( y ’ ) 2 ] 2 3 y ′′ = [ 1 + ( 2 x ) 2 ] 2 3 2 = ( 1 + 4 x 2 ) 2 3 2 .
بنابراین، انحنا و شعاع آن در مبدأ (x = 0 x = 0 x = 0
K ( x = 0 ) = 2 ( 1 + 4 ⋅ 0 2 ) 3 2 = 2 , R = 1 K = 1 2 . \large { K \left ( { x = 0 } \right ) = \frac { 2 } { { { { \left ( { 1 + 4 \cdot { 0 ^ 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = 2 , } \; \; \; \kern-0.3pt { R = \frac { 1 } { K } = \frac { 1 } { 2 } . } K ( x = 0 ) = ( 1 + 4 ⋅ 0 2 ) 2 3 2 = 2 , R = K 1 = 2 1 .
مثال ۳
انحنا و شعاع انحنای منحنی y = cos m x y = \cos mx y = cos m x ماکزیمم آن به دست آورید.
حل: این تابع، در نقطه x = 2 π n m x = {\large\frac{{2\pi n}}{m}\normalsize} x = m 2 πn n ∈ Z n \in Z n ∈ Z x = 0 x =0 x = 0
مشتقهای تابع به صورت زیر هستند:
y ’ = ( cos m x ) ′ = – m sin m x , y ′ ′ = ( – m sin m x ) ′ = – m 2 cos m x . \large \begin {align*} y ’ & = { \left ( { \cos m x } \right ) ^ \prime } = – m \sin m x , \\ \; \; \; \kern-0.3pt y ^ { \prime \prime } & = \left ( { – m \sin m x } \right ) ^ \prime = { – { m ^ 2 } \cos m x . } \end {align*} y ’ y ′′ = ( cos m x ) ′ = – m sin m x , = ( – m sin m x ) ′ = – m 2 cos m x .
در نتیجه، انحنای این منحنی برابر است با:
K = ∣ y ′ ′ ∣ [ 1 + ( y ’ ) 2 ] 3 2 = ∣ – m 2 cos m x ∣ [ 1 + ( – m sin m x ) 2 ] 3 2 = ∣ – m 2 cos m x ∣ ( 1 + m 2 sin 2 m x ) 3 2 . \large \begin {align*} K & = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \left | { – { m ^ 2 } \cos m x } \right | } } { { { { \left [ { 1 + { { \left ( { – m \sin m x } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { \left | { – { m ^ 2 } \cos m x } \right | } } { { { { \left ( { 1 + { m ^ 2 } { { \sin } ^ 2 } m x } \right ) } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } . } \end {align*} K = [ 1 + ( y ’ ) 2 ] 2 3 y ′′ = [ 1 + ( – m sin m x ) 2 ] 2 3 – m 2 cos m x = ( 1 + m 2 sin 2 m x ) 2 3 – m 2 cos m x .
در نقطه ماکزیمم x = 0 x = 0 x = 0
K ( x = 0 ) = m 2 ( 1 + m 2 sin 2 0 ) 3 2 = m 2 , R = 1 K = 1 m 2 . \large { { K \left ( { x = 0 } \right ) = \frac { { { m ^ 2 } } } { { { { \left ( { 1 + { m ^ 2 } { { \sin } ^ 2 } 0 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { m ^ 2 } , } } \; \; \; \kern-0.3pt { { R = \frac { 1 } { K } = \frac { 1 } { { { m ^ 2 } } } . } } K ( x = 0 ) = ( 1 + m 2 sin 2 0 ) 2 3 m 2 = m 2 , R = K 1 = m 2 1 .
مثال ۴
انحنا و شعاع انحنای منحنی تابع y = x y = \sqrt x y = x x = 1 x = 1 x = 1
حل: مشتقات تابع رادیکالی به صورت زیر هستند:
y ’ = ( x ) ′ = 1 2 x , y ′ ′ = ( 1 2 x ) ′ = ( 1 2 x – 1 2 ) ′ = – 1 4 x – 3 2 = – 1 4 x 3 . \large \begin {align*} y ’ & = { \left ( { \sqrt x } \right ) ^ \prime } = \frac { 1 }{ { 2 \sqrt x } } , \\ \; \; \; \kern-0.3pt y ^ { \prime \prime } & = { \left ( { \frac { 1 } { { 2 \sqrt x } } } \right ) ^ \prime } = { { \left ( {\frac { 1 } { 2 } { x ^ { – \large \frac { 1 } { 2 } \normalsize } } } \right ) ^ \prime } } \\ & = { – \frac { 1 } {4 } { x ^ { – \large \frac { 3 } { 2 } \normalsize } } } = { – \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } .} \end {align*} y ’ y ′′ = ( x ) ′ = 2 x 1 , = ( 2 x 1 ) ′ = ( 2 1 x – 2 1 ) ′ = – 4 1 x – 2 3 = – 4 x 3 1 .
انحنای منحنی با رابطه زیر محاسبه میشود:
$$ \large \begin {align*}<br />
\require {cancel} K & = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \left | { – \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } } \right | } } { { { { \left [ { 1 + { { \left ( { \frac { 1 } { { 2 \sqrt x } } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } } } { { { { \left ( {1 + \frac { 1 }{ { 4 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { \frac { 1 } { { 4 \sqrt { { x ^ 3 } } } } } } { { { { \left ( { \frac { { 4 x + 1 } } { { 4 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { { 4 ^ { \large \frac { 3 } { 2 } \normalsize } } \cancel { x ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { 4 \cancel { x ^ { \large \frac { 3 } { 2 } \normalsize } } { { \left ( { 4 x + 1 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 2 } { { { { \left ( { 4 x + 1 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . }<br />
\end {align*} $$
در نقطه x = 1 x = 1 x = 1
K ( x = 1 ) = 2 ( 4 ⋅ 1 + 1 ) 3 2 = 2 5 5 , R ( x = 1 ) = 1 K = 5 5 2 . \large \begin {align*} K ( x & = 1 ) = \frac { 2 } { { { { \left ( { 4 \cdot 1 + 1 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = \frac { 2 } { { 5 \sqrt 5 } } , \; \; \; \kern-0.3pt \\ R ( x & = 1 ) = \frac { 1 }{ K } = \frac { { 5 \sqrt 5 } } { 2 } . \end {align*} K ( x R ( x = 1 ) = ( 4 ⋅ 1 + 1 ) 2 3 2 = 5 5 2 , = 1 ) = K 1 = 2 5 5 .
مثال ۵
منحنی با معادله y 2 + x 3 = 0 {y^2} + {x^3} = 0 y 2 + x 3 = 0 ( − 1 , 1 ) ( -1 , 1 ) ( − 1 , 1 )
حل: ابتدا مشتق ضمنی این تابع را مینویسیم:
y 2 + x 3 = 0 , ⇒ ( y 2 + x 3 ) ′ = 0 , ⇒ 3 x 2 + 2 y y ’ = 0 , ⇒ y ’ = – 3 x 2 2 y . \large \begin {align*} { y ^ 2 } + { x ^ 3 } = 0 , \; \; \Rightarrow { { \left ( { { y ^ 2 } + { x ^ 3 } } \right ) ^ \prime } = 0 , \; \; } \\ \Rightarrow { 3 { x ^ 2 } + 2 y y ’ = 0 , \; \; } \Rightarrow { y ’ = – \frac { { 3 { x ^ 2 } } } { { 2 y } } . } \end {align*} y 2 + x 3 = 0 , ⇒ ( y 2 + x 3 ) ′ = 0 , ⇒ 3 x 2 + 2 yy ’ = 0 , ⇒ y ’ = – 2 y 3 x 2 .
به طریق مشابه، مشتق دوم را به دست میآوریم:
3 x 2 + 2 y y ’ = 0 , ⇒ ( 3 x 2 + 2 y y ’ ) ′ = 0 , ⇒ 6 x + 2 ( y ’ ) 2 + 2 y y ′ ′ = 0 , ⇒ y y ′ ′ + ( y ’ ) 2 + 3 x = 0 , ⇒ y ′ ′ = – ( y ’ ) 2 + 3 x y . \large \begin {align*} 3 { x ^ 2 } + 2 y y ’ = 0 , \; \; & \Rightarrow { { \left ( { 3 { x ^ 2 } + 2 y y ’ } \right ) ^ \prime } = 0 , \; \; } \\ & \Rightarrow { 6 x + 2 { \left ( { y ’ } \right ) ^ 2 } + 2 y y ^ { \prime \prime } = 0 , \; \; } \\ & \Rightarrow { y y ^ { \prime \prime } + { \left ( { y ’ } \right ) ^ 2 } + 3 x = 0 , \; \; } \\ & \Rightarrow { y ^ { \prime \prime } = – \frac { { { { \left ( { y ’ } \right ) } ^ 2 } + 3 x } } { y } .} \end {align*} 3 x 2 + 2 yy ’ = 0 , ⇒ ( 3 x 2 + 2 yy ’ ) ′ = 0 , ⇒ 6 x + 2 ( y ’ ) 2 + 2 y y ′′ = 0 , ⇒ y y ′′ + ( y ’ ) 2 + 3 x = 0 , ⇒ y ′′ = – y ( y ’ ) 2 + 3 x .
با جایگذاری رابطه مشتق اول در رابطه اخیر، داریم:
y ′ ′ = – ( y ’ ) 2 + 3 x y = – ( – 3 x 2 2 y ) 2 + 3 x y = – 9 x 4 4 y 2 + 3 x y = – 9 x 4 + 12 x y 2 4 y 3 . \large \begin {align*} y ^ { \prime \prime } & = – \frac { { { { \left ( { y ’ } \right ) } ^ 2 } + 3 x } } { y } = { – \frac { { { { \left ( { – \frac { { 3 { x ^ 2 } } } { { 2 y } } } \right ) } ^ 2 } + 3 x } } { y } } \\ & = { – \frac { { \frac { { 9 { x ^ 4 } } } { { 4 { y ^ 2 } } } + 3 x } } { y } } = { – \frac { { 9 { x ^ 4 } + 1 2 x { y ^ 2 } } } { { 4{ y ^ 3 } } } . } \end {align*} y ′′ = – y ( y ’ ) 2 + 3 x = – y ( – 2 y 3 x 2 ) 2 + 3 x = – y 4 y 2 9 x 4 + 3 x = – 4 y 3 9 x 4 + 12 x y 2 .
اکنون مقادیر مشتقها را در نقطه ( – 1 , 1 ) \left( { – 1,1} \right) ( –1 , 1 )
y ’ ( – 1 , 1 ) = – 3 ⋅ ( – 1 ) 2 2 ⋅ 1 = – 3 2 , y ′ ′ ( – 1 , 1 ) = – 9 ⋅ ( – 1 ) 4 + 12 ⋅ ( – 1 ) ⋅ 1 2 4 ⋅ 1 3 = 3 4 . \large \begin {align*} y ’ \left ( { – 1 , 1 } \right ) & = – \frac { { 3 \cdot { { \left ( { – 1 } \right ) } ^ 2 } } } { { 2 \cdot 1 } } = – \frac { 3 } { 2 } , \\ y ^ { \prime \prime } \left ( { – 1 , 1 } \right ) & = \kern0pt { – \frac { { 9 \cdot { { \left ( { – 1 } \right ) } ^ 4 } + 1 2 \cdot \left ( { – 1 } \right ) \cdot { 1 ^ 2 } } } { { 4 \cdot { 1 ^ 3 } } } } = { \frac { 3 } { 4 } . } \end {align*} y ’ ( –1 , 1 ) y ′′ ( –1 , 1 ) = – 2 ⋅ 1 3 ⋅ ( –1 ) 2 = – 2 3 , = – 4 ⋅ 1 3 9 ⋅ ( –1 ) 4 + 12 ⋅ ( –1 ) ⋅ 1 2 = 4 3 .
در نتیجه، انحنای منحنی در نقطه ( − 1 , 1 ) (-1 , 1) ( − 1 , 1 )
K = ∣ y ′ ′ ∣ [ 1 + ( y ’ ) 2 ] 3 2 = 3 4 [ 1 + ( – 3 2 ) 2 ] 3 2 = 3 4 ( 1 + 9 4 ) 3 2 = 3 4 ⋅ 4 3 2 13 3 2 = 6 13 3 2 ≈ 0.128. \large \begin {align*} K & = \frac { { \left | { y ^ { \prime \prime } } \right | } }{ { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \frac { 3 } { 4 } } } { { { { \left [ { 1 + { { \left ( { – \frac { 3 }{ 2 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } } \\ & = { \frac { { \frac { 3 } { 4 } } }{ { { { \left ( { 1 + \frac { 9 } { 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 3 } { 4 } \cdot \frac { { { 4 ^ {\large \frac { 3 } { 2 } \normalsize } } } } { { { {1 3 } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 6 } { { { { 1 3 } ^ { \large \frac { 3 } { 2 } \normalsize } } } } \approx 0.128 . } \end {align*} K = [ 1 + ( y ’ ) 2 ] 2 3 y ′′ = [ 1 + ( – 2 3 ) 2 ] 2 3 4 3 = ( 1 + 4 9 ) 2 3 4 3 = 4 3 ⋅ 13 2 3 4 2 3 = 13 2 3 6 ≈ 0.128.
مثال ۶
انحنای دلوار r = a ( 1 + cos θ ) r = a\left( {1 + \cos \theta } \right) r = a ( 1 + cos θ ) θ = 0 \theta = 0 θ = 0
حل: برای محاسبه انحنای منحنی، از فرمول زیر استفاده میکنیم:
K = ∣ r 2 + 2 ( r ’ ) 2 – r r ′ ′ ∣ [ r 2 + ( r ’ ) 2 ] 3 2 . \large K = \frac { { \left | { { r ^ 2 } + 2 { { \left ( { r ’ } \right ) } ^ 2 } – r r ^ { \prime \prime } } \right | } } { { { { \left [ { { r ^ 2 } + { { \left ( { r ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . K = [ r 2 + ( r ’ ) 2 ] 2 3 r 2 + 2 ( r ’ ) 2 – r r ′′ .
مشتقهای منحنی قطبی برابرند با:
r ’ = [ a ( 1 + cos θ ) ] ′ = – a sin θ , r ′ ′ = ( – a sin θ ) ′ = – a cos θ . \large \begin {align*} r ’ & = { \left [ { a \left ( { 1 + \cos \theta } \right ) } \right ] ^ \prime } = – a \sin \theta , \\ \; \; \; \kern-0.3pt r ^ { \prime \prime } & = { \left ( { – a \sin \theta } \right ) ^ \prime } = – a \cos \theta . \end {align*} r ’ r ′′ = [ a ( 1 + cos θ ) ] ′ = – a sin θ , = ( – a sin θ ) ′ = – a cos θ .
با جایگذاری مشتقهای بالا در معادله انحنا و کمی سادهسازی، داریم:
K = 3 2 3 2 a ( 1 + cos θ ) 1 2 . \large { K } = { \frac { 3 } { { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a { { \left ( { 1 + \cos \theta } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } } . } K = 2 2 3 a ( 1 + cos θ ) 2 1 3 .
بنابراین، وقتی θ = 0 \theta = 0 θ = 0
K ( θ = 0 ) = 3 2 3 2 a ( 1 + cos θ ) 1 2 = 3 2 3 2 2 1 2 a = 3 4 a . \large { K \left ( { \theta = 0 } \right ) } = { \frac { 3 } { { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a { { \left ( { 1 + \cos \theta } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } } } } = { \frac { 3 } { { { 2 ^ { \large \frac { 3 }{ 2 } \normalsize } } { 2 ^ { \large \frac { 1 } { 2 } \normalsize } } a } } } = { \frac { 3 } { { 4 a } } . } K ( θ = 0 ) = 2 2 3 a ( 1 + cos θ ) 2 1 3 = 2 2 3 2 2 1 a 3 = 4 a 3 .
مثال ۷
انحنای دلوار r = a ( 1 + cos θ ) r = a\left( {1 + \cos \theta } \right) r = a ( 1 + cos θ ) θ = 0 \theta = 0 θ = 0
حل: شعاع انحنای منحنی پارامتری با فرمول زیر قابل محاسبه است:
R = [ ( x ’ ) 2 + ( y ’ ) 2 ] 3 2 ∣ x ’ y ′ ′ – y ’ x ′ ′ ∣ . \large R = \frac { { { { \left [ { { { \left ( { x ’ } \right ) } ^ 2 } + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { x ’ y ^ { \prime \prime } – y ’ x ^ { \prime \prime } } \right | } } . R = ∣ x ’ y ′′ – y ’ x ′′ ∣ [ ( x ’ ) 2 + ( y ’ ) 2 ] 2 3 .
مشتقها به صورت زیر محاسبه میشوند:
x ’ = [ a ( t – sin t ) ] ′ = a ( 1 – cos t ) , x ′ ′ = [ a ( 1 – cos t ) ] ′ = a sin t , y ’ = [ a ( 1 – cos t ) ] ′ = a sin t , y ′ ′ = ( a sin t ) ′ = a cos t . \large \begin {align*} x ’ & = { \left [ { a \left ( { t – \sin t } \right ) } \right ] ^ \prime } = a \left ( { 1 – \cos t } \right ) , \\ \; \; \; \kern-0.3pt x ^ { \prime \prime } & = { \left [ { a \left ( { 1 – \cos t } \right ) } \right ] ^ \prime } = a \sin t , \\ y ’ & = { \left [ { a \left ( { 1 – \cos t } \right ) } \right ] ^ \prime } = a \sin t , \; \; \; \kern-0.3pt \\ y ^ { \prime \prime } & = { \left ( { a \sin t } \right ) ^ \prime } = a \cos t . \end {align*} x ’ x ′′ y ’ y ′′ = [ a ( t – sin t ) ] ′ = a ( 1– cos t ) , = [ a ( 1– cos t ) ] ′ = a sin t , = [ a ( 1– cos t ) ] ′ = a sin t , = ( a sin t ) ′ = a cos t .
با جایگذاری مشتقات بالا در معادله شعاع انحنا، داریم:
R = [ 2 a 2 ( 1 – cos t ) ] 3 2 ∣ a 2 ( cos t – 1 ) ∣ = 2 3 2 a 3 ( 1 – cos t ) 3 2 a 2 ( 1 – cos t ) = 2 3 2 a ( 1 – cos t ) 1 2 = 2 3 2 a ⋅ ( 2 sin 2 t 2 ) 1 2 = 4 a ( sin 2 t 2 ) 1 2 . \large \begin {align*} R & = { \frac { { { { \left [ { 2 { a ^ 2 } \left ( { 1 – \cos t } \right ) } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { { a ^ 2 } \left ( { \cos t – 1 } \right ) } \right | } } } = { \frac { { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } { a ^ 3 } { { \left ( { 1 – \cos t } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { { a ^ 2 } \left ( { 1 – \cos t } \right ) } } } \\ & = { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a { \left ( { 1 – \cos t } \right ) ^ { \large \frac { 1 } { 2 } \normalsize } } } = { { 2 ^ { \large \frac { 3 } { 2 } \normalsize } } a \cdot { \left ( { 2 { { \sin } ^ 2 } \frac { t } { 2 } } \right ) ^ { \large \frac { 1 } { 2 } \normalsize } } } \\ & = { 4 a { \left ( { { { \sin } ^ 2 } \frac { t } { 2 } } \right ) ^ { \large \frac { 1 } {2 } \normalsize } } . } \end {align*} R = a 2 ( cos t –1 ) [ 2 a 2 ( 1– cos t ) ] 2 3 = a 2 ( 1– cos t ) 2 2 3 a 3 ( 1– cos t ) 2 3 = 2 2 3 a ( 1– cos t ) 2 1 = 2 2 3 a ⋅ ( 2 sin 2 2 t ) 2 1 = 4 a ( sin 2 2 t ) 2 1 .
کمان اول چرخزاد، یعنی بازه 0 ≤ t ≤ 2 π 0 \le t \le 2\pi 0 ≤ t ≤ 2 π
R = 4 a sin t 2 . \large R = 4 a \sin \frac { t } { 2 } . R = 4 a sin 2 t .
با توجه به رابطه بالا، مشاهده ميکنیم که حداکثر شعاع انحنا در t = π t = \pi t = π R max = 4 a {R_{\max }} = 4a R m a x = 4 a
مثال ۸
انحنای منحنی y = arctan x y = \arctan x y = arctan x x = 0 x = 0 x = 0
حل: مشتقات تابع y = arctan x y = \arctan x y = arctan x
y ’ = ( arctan x ) ′ = 1 1 + x 2 , y ′ ′ = ( 1 1 + x 2 ) ′ = – 2 x ( 1 + x 2 ) 2 . \large y ’ = { \left ( { \arctan x } \right ) ^ \prime } = \frac { 1 } { { 1 + { x ^ 2 } } } , \; \; \; \kern-0.3pt \\ \large { y ^ { \prime \prime } = { \left ( { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) ^ \prime } } = { – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } .} y ’ = ( arctan x ) ′ = 1 + x 2 1 , y ′′ = ( 1 + x 2 1 ) ′ = – ( 1 + x 2 ) 2 2 x .
انحنای منحنی معکوس تانژانت به صورت زیر بیان میشود:
$$ \large \begin {align*}<br />
K & = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } = { \frac { { \left | { – \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } \right | } } { { { { \left [ { 1 + { { \left ( { \frac { 1 } { { 1 + { x ^ 2 } } } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { \frac { { 2 x } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } } { { { { \left [ { \frac { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } } { { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { 2 x { { \left ( { 1 + { x ^ 2 } } \right ) } ^ \cancel { 3 } } } } { { { \cancel { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } } { { \left [ { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \frac { { 2 x \left ( { 1 + { x ^ 2 } } \right ) } } { { { { \left [ { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } \right ] } ^ { \large \frac {3 } {2 } \normalsize } } } } . }<br />
\end {align*} $$
همانطور که میبینیم، در نقطه x = 0 x = 0 x = 0
K ( 0 ) = K 0 = 0 \large K \left ( 0 \right ) = { K _ 0 } = 0 K ( 0 ) = K 0 = 0
در این حالت، نقطه x = 0 x = 0 x = 0 نقطه عطف تابع y = arctan x y = \arctan x y = arctan x
اکنون مقدار انحنای K ∞ {K_{\infty}} K ∞ x → ∞ x \to \infty x → ∞
K ∞ = lim x → ∞ K ( x ) = lim x → ∞ 2 x ( 1 + x 2 ) [ ( 1 + x 2 ) 2 + 1 ] 3 2 = lim x → ∞ 2 x 3 + 2 x ( x 4 + 2 x 2 + 2 ) 3 2 = lim x → ∞ 2 x 3 + 2 x x 6 ( x 4 + 2 x 2 + 2 ) 3 2 x 6 = lim x → ∞ 2 x 3 + 2 x 5 ( x 4 + 2 x 2 + 2 x 4 ) 3 2 = lim x → ∞ 2 x 3 + 2 x 5 ( 1 + 2 x 2 + 2 x 4 ) 3 2 = 0 1 = 0. \large \begin {align*} { K _ \infty } & = \lim \limits _ { x \to \infty } K \left ( x \right ) = { \lim \limits _ { x \to \infty } \frac { { 2 x \left ( { 1 + { x ^ 2 } } \right ) } } { { { { \left [ { { { \left ( { 1 + { x ^ 2 } } \right ) } ^ 2 } + 1 } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } \\ & = { \lim \limits _ { x \to \infty } \frac { { 2 { x ^ 3 } + 2 x } } { { { { \left ( { { x ^ 4 } + 2 { x ^ 2 } + 2 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \lim \limits _ { x \to \infty } \frac { { \frac { { 2 { x ^ 3 } + 2 x } } { { { x ^ 6 } } } } }{{ \frac { { { { \left ( { { x ^ 4 } + 2 { x ^ 2 } + 2 } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { { x ^ 6 } } } } } } \\ & = { \lim \limits _ { x \to \infty } \frac { { \frac { 2 } { { { x ^ 3 } } } + \frac { 2 } { { { x ^ 5 } } } } } { { { { \left ( { \frac { { { x ^ 4 } + 2 { x ^ 2 } + 2 } } { { { x ^ 4 } } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \lim \limits _ { x \to \infty } \frac { { \frac { 2 } { { { x ^ 3 } } } + \frac { 2 } { { { x ^ 5 } } } } } { { { { \left ( { 1 + \frac { 2 } { { { x ^ 2 } } } + \frac { 2 } { { { x ^ 4 } } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { 0 } { 1 } = 0 . } \end {align*} K ∞ = x → ∞ lim K ( x ) = x → ∞ lim [ ( 1 + x 2 ) 2 + 1 ] 2 3 2 x ( 1 + x 2 ) = x → ∞ lim ( x 4 + 2 x 2 + 2 ) 2 3 2 x 3 + 2 x = x → ∞ lim x 6 ( x 4 + 2 x 2 + 2 ) 2 3 x 6 2 x 3 + 2 x = x → ∞ lim ( x 4 x 4 + 2 x 2 + 2 ) 2 3 x 3 2 + x 5 2 = x → ∞ lim ( 1 + x 2 2 + x 4 2 ) 2 3 x 3 2 + x 5 2 = 1 0 = 0.
بنابراین، انحنای منحنی معکوس تانژانت در بینهایت نیز به صفر میل میکند. این بدین معنی است که مقدار ماکزیمم انحنا در مقادیر میانی x x x
مثال ۹
کوچکترین شعاع انحنای تابع نمایی y = e x y = e ^ x y = e x
حل: تابع نمایی y = e x y = e ^ x y = e x
K = ∣ y ′ ′ ∣ [ 1 + ( y ’ ) 2 ] 3 2 = e x ( 1 + e 2 x ) 3 2 . \large { K = \frac { { \left | { y ^ { \prime \prime } } \right | } } { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } } = { \frac { { { e ^ x } } } { { { { \left ( { 1 + { e ^ { 2 x } }} \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } . } K = [ 1 + ( y ’ ) 2 ] 2 3 y ′′ = ( 1 + e 2 x ) 2 3 e x .
میتوان از علامت قدر مطلق در صورت کسر رابطه بالا چشم پوشید، زیرا تابع نمایی همیشه مثبت است.
شعاع انحنا برابر است با:
R = 1 K = ( 1 + e 2 x ) 3 2 e x . \large R = \frac { 1 } { K } = \frac { { { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { { e ^ x } } } . R = K 1 = e x ( 1 + e 2 x ) 2 3 .
مقدار R R R x x x R R R x x x
R ’ ( x ) = [ ( 1 + e 2 x ) 3 2 e x ] ′ = e x ( 1 + e 2 x ) 1 2 [ 3 e 2 x – ( 1 + e 2 x ) ] e 2 x = ( 1 + e 2 x ) 1 2 ( 2 e 2 x – 1 ) e x . \large \begin {align*} R ’ \left ( x \right ) & = { \left [ { \frac { { { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { {{ e ^ x } } } } \right ] ^ \prime } \\ & = { \frac { { { e ^ x } { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left [ { 3 { e ^ { 2 x } } – \left ( { 1 + { e ^ { 2 x } } } \right ) } \right ] } } { { { e ^ { 2 x } } } } } \\ & = { \frac { { { { \left ( { 1 + { e ^ { 2 x } } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left ( { 2 { e ^ { 2 x } } – 1 } \right ) } }{ { { e ^ x } } } . } \end {align*} R ’ ( x ) = e x ( 1 + e 2 x ) 2 3 ′ = e 2 x e x ( 1 + e 2 x ) 2 1 [ 3 e 2 x – ( 1 + e 2 x ) ] = e x ( 1 + e 2 x ) 2 1 ( 2 e 2 x –1 ) .
تابع R ( x ) R (x) R ( x )
R ’ ( x ) = 0 , ⇒ 2 e 2 x – 1 = 0 , ⇒ e 2 x = 1 2 , ⇒ 2 x = ln 1 2 = – ln 2 , ⇒ x = – ln 2 2 ≈ – 0.35. \large \begin {align*} & R ’ \left ( x \right ) = 0 , \; \; \Rightarrow { 2 { e ^ { 2x } } – 1 = 0 , \; \; } \Rightarrow { { e ^ { 2 x } } = \frac { 1 } { 2 } , \; \; } \\ & \Rightarrow { 2 x = \ln \frac { 1 } { 2 } = – \ln 2 , \; \; } \Rightarrow { x = – \frac { { \ln 2 } } { 2 } \approx – 0.35 . } \end {align*} R ’ ( x ) = 0 , ⇒ 2 e 2 x –1 = 0 , ⇒ e 2 x = 2 1 , ⇒ 2 x = ln 2 1 = – ln 2 , ⇒ x = – 2 ln 2 ≈ –0.35.
مشتق R ′ ( x ) R^\prime\left( x \right) R ′ ( x ) R ( x ) R(x ) R ( x )
R min = R ( – ln 2 2 ) = [ 1 + e 2 ⋅ ( – ln 2 2 ) ] 3 2 e – ln 2 2 = [ 1 + e ln 1 2 ] 3 2 e ln 1 2 = ( 1 + 1 2 ) 3 2 1 2 = 2 ( 3 2 ) 3 2 ≈ 2.60. \large \begin {align*} { R _ { \min } } & = R \left ( { – \frac { { \ln 2 } } { 2 } } \right ) = { \frac { { { { \left [ { 1 + { e ^ { 2 \cdot \left ( { – \large \frac { { \ln 2 } } { 2 } \normalsize } \right ) } } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { {e ^ { – \large \frac { { \ln 2 } } { 2 } \normalsize } } } } } \\ & = { \frac { { { { \left [ { 1 + { e ^ { \ln \large \frac { 1 } { 2 } \normalsize } } } \right ] } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } { { { e ^ { \ln \large \frac { 1 } { { \sqrt 2 } } \normalsize } } } } } = { \frac { { { { \left ( { 1 + \frac { 1 } { 2 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 1 } { { \sqrt 2 } } } } } = { \sqrt 2 { \left ( { \frac { 3 } { 2 } } \right ) ^ { \large \frac { 3 } { 2 } \normalsize } } \approx 2.60 . } \end {align*} R m i n = R ( – 2 ln 2 ) = e – 2 l n 2 [ 1 + e 2 ⋅ ( – 2 l n 2 ) ] 2 3 = e l n 2 1 [ 1 + e l n 2 1 ] 2 3 = 2 1 ( 1 + 2 1 ) 2 3 = 2 ( 2 3 ) 2 3 ≈ 2.60.
مثال ۱۰
کمینه شعاع انحنای سهمی مرتبه سوم y = x 3 y = {x^3} y = x 3
حل: مشتقهای تابع به صورت زیر هستند:
y ’ = ( x 3 ) ′ = 3 x 2 , y ′ ′ = ( 3 x 2 ) ′ = 6 x \large { y ’ = { \left ( { { x ^ 3 } } \right ) ^ \prime } = 3 { x ^ 2 } , } \; \; \; \kern-0.3pt { y ^ { \prime \prime } = { \left ( { 3 { x ^ 2 } } \right ) ^ \prime } = 6 x } y ’ = ( x 3 ) ′ = 3 x 2 , y ′′ = ( 3 x 2 ) ′ = 6 x
شعاع منحنی تابع با رابطه زیر به دست میآید:
R = [ 1 + ( y ’ ) 2 ] 3 2 ∣ y ′ ′ ∣ = [ 1 + ( 3 x 2 ) 2 ] 3 2 ∣ 6 x ∣ = ( 1 + 9 x 4 ) 3 2 ∣ 6 x ∣ . \large { R = \frac { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } } \right | } } } = { \frac { { {{ \left [ { 1 + { { \left ( { 3 { x ^ 2 } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 }{ 2 } \normalsize } } } } { { \left | { 6 x } \right | } } } = { \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { 6 x } \right | } } . } R = ∣ y ′′ ∣ [ 1 + ( y ’ ) 2 ] 2 3 = ∣ 6 x ∣ [ 1 + ( 3 x 2 ) 2 ] 2 3 = ∣ 6 x ∣ ( 1 + 9 x 4 ) 2 3 .
سهمی مکعب داده شده حول مبدأ متقارن است. به همین دلیل، بخشی از آن را در نظر میگیریم که x > 0 x > 0 x > 0 R R R x x x
R ( x ) = ( 1 + 9 x 4 ) 3 2 6 x . \large R \left ( x \right ) = \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } }{ { 6 x } } . R ( x ) = 6 x ( 1 + 9 x 4 ) 2 3 .
حال مشتق شعاع انحنا را مینویسیم:
R ’ ( x ) = [ ( 1 + 9 x 4 ) 3 2 6 x ] ′ = ( ( 1 + 9 x 4 ) 3 2 ) ′ 6 x – ( 1 + 9 x 4 ) 3 2 ( 6 x ) ′ 36 x 2 = 6 ( 1 + 9 x 4 ) 1 2 [ 54 x 4 – ( 1 + 9 x 4 ) ] 36 x 2 = ( 1 + 9 x 4 ) 1 2 ( 45 x 4 – 1 ) 6 x 2 . \large \begin {align*} R ’ \left ( x \right ) & = { \left [ { \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } }} { { 6 x } } } \right ] ^ \prime } = { \frac { { { { \left ( { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 }{ 2 } \normalsize } } } \right ) } ^ \prime } 6 x – { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } { { \left ( { 6 x } \right ) } ^ \prime } } } { { 3 6 { x ^ 2 } } } } \\ & = { \frac { { 6 { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left [ { 5 4 { x ^ 4 } – \left ( { 1 + 9 { x ^ 4} } \right ) } \right ] } } { { 3 6 { x ^ 2 } } } } = { \frac { { { { \left ( { 1 + 9 { x ^ 4 } } \right ) } ^ { \large \frac { 1 } { 2 } \normalsize } } \left ( { 4 5 { x ^ 4 } – 1 } \right ) } } { { 6 { x ^ 2 } }} . } \end {align*} R ’ ( x ) = 6 x ( 1 + 9 x 4 ) 2 3 ′ = 36 x 2 ( ( 1 + 9 x 4 ) 2 3 ) ′ 6 x – ( 1 + 9 x 4 ) 2 3 ( 6 x ) ′ = 36 x 2 6 ( 1 + 9 x 4 ) 2 1 [ 54 x 4 – ( 1 + 9 x 4 ) ] = 6 x 2 ( 1 + 9 x 4 ) 2 1 ( 45 x 4 –1 ) .
در x > 0 x > 0 x > 0
45 x 4 – 1 = 0 , ⇒ x 4 = 1 45 , ⇒ x = 1 45 4 ≈ 0.39. \large { 4 5 { x ^ 4 } – 1 = 0 , \; \; } \Rightarrow { { x ^ 4 } = \frac { 1 } { { 4 5 } } , \; \; } \Rightarrow { x = \frac { 1 }{ { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } \approx 0.39 . } 45 x 4 –1 = 0 , ⇒ x 4 = 45 1 , ⇒ x = 4 45 1 ≈ 0.39.
وقتی از این نقطه بگذریم، R ’ ( x ) R’\left( x \right) R ’ ( x )
y ’ ( 1 45 4 ) = 3 ⋅ ( 1 45 4 ) 2 = 3 45 , y ′ ′ ( 1 45 4 ) = 6 45 4 \large \begin {align*} y ’ \left ( { \frac { 1 } { { \sqrt [ \large 4 \normalsize ]{ { 4 5 } } } } } \right ) & = 3 \cdot { \left ( { \frac { 1 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } } \right ) ^ 2 } = \frac { 3 } { { \sqrt { 4 5 } } } , \; \; \; \kern-0.3pt \\ y ^ { \prime \prime } \left ( { \frac { 1 } { { \sqrt [ \large 4 \normalsize ]{ { 4 5 } } } } } \right ) & = \frac { 6 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } \end {align*} y ’ ( 4 45 1 ) y ′′ ( 4 45 1 ) = 3 ⋅ ( 4 45 1 ) 2 = 45 3 , = 4 45 6
⇒ R min = [ 1 + ( y ’ ) 2 ] 3 2 ∣ y ′ ′ ∣ = [ 1 + ( 3 45 ) 2 ] 3 2 6 45 4 = ( 1 + 9 45 ) 3 2 6 45 4 = ( 54 45 ) 3 2 ⋅ 45 4 6 = 2 3 2 ⋅ ( 3 3 ) 3 2 ⋅ 5 1 4 ⋅ ( 3 2 ) 1 4 ( 3 3 ) 3 2 ⋅ 5 3 2 ⋅ 2 ⋅ 3 = 2 1 2 ⋅ 3 5 5 4 = ≈ 0.57. \large \begin {align*} \Rightarrow { R _ { \min } } & = \frac { { { { \left [ { 1 + { { \left ( { y ’ } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \left | { y ^ { \prime \prime } } \right | } } = { \frac { { { { \left [ { 1 + { { \left ( { \frac { 3 } { { \sqrt { 4 5 } } } } \right ) } ^ 2 } } \right ] } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 6 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } } } } \\ & = { \frac { { { { \left ( { 1 + \frac { 9 } { { 4 5 } } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } } } { { \frac { 6 } { { \sqrt [ \large 4 \normalsize ] { { 4 5 } } } } } } } = { { \left ( { \frac { { 5 4 } } { { 45 } } } \right ) ^ { \large \frac { 3 }{ 2 } \normalsize } } \cdot \frac { { \sqrt [ \large 4 \normalsize ]{ { 4 5 } } } } { 6 } } \\ & = { \frac { { { 2 ^ { \large \frac { 3 }{ 2 } \normalsize } } \cdot { { \left ( { { 3 ^ 3 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot { 5 ^ { \large \frac { 1 } { 4 } \normalsize } } \cdot { { \left ( { { 3 ^ 2 } } \right ) } ^ { \large \frac { 1 } { 4 } \normalsize } } } } { { { { \left ( { { 3 ^ 3 } } \right ) } ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot { 5 ^ { \large \frac { 3 } { 2 } \normalsize } } \cdot 2 \cdot 3 } } } \\ & = { \frac { { { 2 ^ { \large \frac { 1 } { 2 } \normalsize } } \cdot 3 } } { { { 5 ^ { \large \frac { 5 } { 4 } \normalsize } } } } } = { \approx 0.5 7 . } \end {align*} ⇒ R m i n = ∣ y ′′ ∣ [ 1 + ( y ’ ) 2 ] 2 3 = 4 45 6 [ 1 + ( 45 3 ) 2 ] 2 3 = 4 45 6 ( 1 + 45 9 ) 2 3 = ( 45 54 ) 2 3 ⋅ 6 4 45 = ( 3 3 ) 2 3 ⋅ 5 2 3 ⋅ 2 ⋅ 3 2 2 3 ⋅ ( 3 3 ) 2 3 ⋅ 5 4 1 ⋅ ( 3 2 ) 4 1 = 5 4 5 2 2 1 ⋅ 3 = ≈ 0.57.
اگر علاقهمند به یادگیری مباحث مشابه مطلب بالا هستید، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
^^













با سلام
انحنای کره و استوانه واکر چی
سلام ممنون از مطلب خوبتون.
من برنامه نویسم و میخوام نمودار گذرنده از n نقطه ای که دارمو رسم کنم.
الان با بدست اوردن نقاط عطف و ماکزیموم و مینیموم ها بعلاوه n نقطه ای که دارم اینکارو میکنم اما میخوام اگر بشه تابع منحنی نمودار رو محاسبه کنم که نمودارم دقیق بشه.
میتونید راهشو برام ارسال کنید؟
سلام، ممنون از مطالب خوبتون عالی بود. یه سوال:
انحنای منحنی ( t, t^2 ,t^3) در ( 0,0,0) چند میشه؟
سلام
سایت خوبی ست اولین چیز را با بهترین محتوی در هر موضوعی را می توان توی این سایت یاد گرفت
pdf بذارید ، چه طرز جزوه نویسیه