اعداد با توان کسری | به زبان ساده
در آموزشهای قبلی مجله فرادرس، به اعدادی پرداختیم که توان آنها منفی است و روش محاسبه این اعداد را بررسی کردیم. در این آموزش، با روش محاسبه عباراتی با توان کسری آشنا میشویم.


توان کسری و رادیکال
در آموزش رادیکال از مجله فرادرس با رابطه بین رادیکال و توان آشنا شدیم. دیدیم که یک رادیکال توان را نتیجه میدهد و با توان نیز میتوان یک ریشه رادیکالی را بیان کرد.
برای مثال:
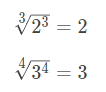
اما رابطه دیگری نیز وجود دارد که با استفاده از آن میتوانیم محاسبات را سادهتر انجام دهیم.
هر عدد با توان کسری را میتوان با یک عدد رادیکالی نیز نشان داد. عکس این مطلب نیز صحیح است. یعنی هر رادیکال با فرجه و توان مشخص را میتوان در قالب یک عدد با توان کسری نوشت. رابطه عدد با توان کسری و رادیکال به شکل زیر است:
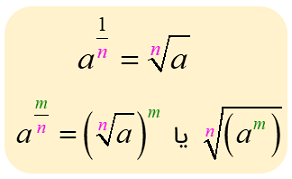
برای جذر یا همان ریشه دوم، توان یکدوم را میتوانیم به فرم زیر بنویسیم:
یا
برای ریشه سوم نیز داریم:
ریشه چهارم را نیز میتوانیم به صورت زیر بنویسیم:
به همین ترتیب، ریشه پنجم عدد برابر با عدد با توان یکپنجم است و به همین صورت ادامه پیدا میکند.
به دو مثال ابتدای متن دقت کنید. این دو مثال را میتوانیم به صورت زیر بنویسیم:
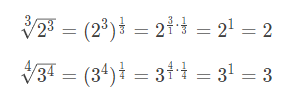
همه ما با توانهای صحیح (مثبت و منفی) آشنایی داریم.
چگونه اعداد با توان کسری را ساده کنیم؟
پرسشی که اغلب پیش میآید، این است که یک عدد با توان کسری را چگونه ساده کنیم و به صورت یک عدد بدون توان بنویسیم.
یا اینکه چگونه اعداد با توان کسری را با ماشینحسابهای ساده محاسبه کنیم. کار ساده است. یک راه آسان این است که اعداد با توان کسری را به صورت رادیکال بنویسیم.
برای مثال، عدد زیر را در نظر بگیرید که توان آن کسری است:
یک راه این است که این عدد را به صورت رادیکالی زیر بنویسیم:
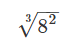
گاهی برای سادهسازی اعداد میتوانیم آنها را به صورت توانی بنویسیم و توان را اعمال کنیم.
نکته: دقت کنید که برای اعمال توان، ابتدا از داخلیترین پرانتز شروع میکنیم.
ضرب اعداد با توان کسری
ضرب اعداد با توان کسری، مشابه ضرب اعداد با توان صحیح است. بدین معنا که اگر پایه دو عدد مشابه باشد، نمای آنها را با هم جمع میکنیم. یعنی، برای ضرب دو عدد و ، داریم:
مثال ضرب اعداد با توان کسری
حاصل ضرب زیر را به دست آورید:
حل: چون مبنای دو عدد یکسان هستند، توانها را با هم جمع میکنیم:

تقسیم اعداد با توان کسری
تقسیم اعداد با توان کسری نیز مشابه تقسیم اعداد با توان صحیح است. بدین معنا که اگر پایه دو عدد مشابه باشد، نمای آنها را از هم کم میکنیم. یعنی، برای تقسیم دو عدد و ، داریم:
مثال تقسیم اعداد با توان کسری
حاصل تقسیم زیر را به دست آورید:
حل: با توجه به قانون تقسیم اعداد با توان کسری، داریم:
توان کسری منفی
اگر توان کسری و همچنین، عدد مثبت باشند، آنگاه توان برای محاسبه اعدادی با توان کسری منفی میتوانیم از فرمول زیر استفاده کنیم:
در حالت کلی، اگر عدد کسری به توان کسر منفی برسد، به صورت زیر محاسبه میشود:
در فرمولهای بالا از این نکته استفاده شده که هر عدد به توان یک عدد منفی، برابر با وارون آن عدد به همان توان با علامت مثبت است.
مثال اول توان کسری منفی
عدد زیر را ساده کنید:
حل: با توجه به آنچه گفتیم، این عدد به صورت زیر محاسبه میشود:
مثال دوم توان کسری منفی
عدد زیر توان کسری منفی زیر را ساده کنید:
حل: با استفاده از قاعده توان منفی، عبارت بالا به صورت زیر ساده میشود:

توان کسری در ماشین حساب
برای مثال اگر بخواهیم عبارت را در ماشینحساب محاسبه کنیم، باید آن را به صورت زیر بنویسیم.
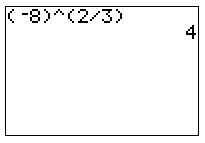
البته دقت کنید که گاهی تنظیمات ماشینحساب به گونهای است که ممکن است عدد به دست آمده درست نباشد. برای مثال، ممکن است یک عدد مختلط یا حتی خطا را نتیجه دهد. بنابراین، حتماً از صحت تنظیمات ماشینحساب مطمئن باشید. شکل زیر این مورد را نشان میدهد.

البه در این موارد، با اندکی تغییرات در نحوه وارد کردن عملگرها، میتوان به نتیجه صحیح دست یافت. شکل زیر نشان میدهد که با تغییر در فرمولنویسی، نتیجه صحیح ۴ به دست آمده است.
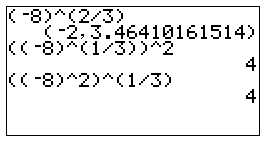
چند مثال از توان کسری
در این بخش، چند مثال متنوع را حل میکنیم.
مثال اول توان کسری
عبارت را ساده کنید.
حل: این مثال نکته مهمی دارد. در نکاه نخست، ممکن است با استفاده از قانون توان بگوییم که جواب به صورت زیر است:
اما این جواب غلط است.
طبق قاعده ترتیب عملیات، باید ابتدا پرانتز داخلی را محاسبه کنیم و پس از آن سراغ سایر محاسبات برویم. بنابراین، جواب صحیح این مثال به صورت زیر محاسبه میشود:
مثال دوم توان کسری
حاصل عبارت را محاسبه کنید.
حل: این عبارت به صورت زیر ساده میشود:
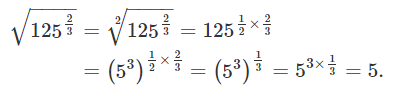
مثال سوم توان کسری
مقدار را از معادله زیر به دست آورید.
حل: از آنجا که ، با برابر قرار دادن آن با مقدار را به دست میآوریم.
مثال چهارم توان کسری
عبارت را ساده کنید.
حل: جواب این مثال به صورت زیر است:

مثال پنجم توان کسری
مقدار را در معادله زیر به دست آورید:
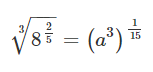
حل: سمت راست معادله به صورت زیر ساده میشود:
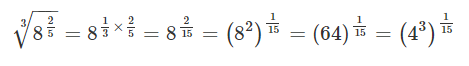
بنابراین، با برابر قرار دادن آن با سمت راست معادله، یعنی ، جواب به دست خواهد آمد.
مثال ششم توان کسری
عبارت را ساده کنید.
حل: ساده شده این عبارت به صورت زیر است:
مثال هفتم توان کسری
عبارت زیر را ساده کنید:
حل: شاید در ابتدا ظاهر این عبارت ترسناک و دشوار به نظر برسد، اما با قواعدی که یاد گرفتهایم و پیادهسازی گام به گام آنها به راحتی میتوانیم این عبارت را ساده کنیم.
ابتدا توانهای منفی را مثبت میکنیم. برای این کار، کافی است عباراتی را که توان منفی دارند، از صورت به مخرج و بالعکس جابهجا کنیم. در این صورت، خواهیم داشت:
اکنون، جملات با پایههای مشابه ( و ) را ساده میکنیم:
گام نهایی، اعمال توان کسری به عبارت است:
مثال هشتم توان کسری
حاصل عبارت زیر را به دست آورید:
حل: با توجه به نکاتی که گفتیم، این عبارت به صورت زیر ساده میشود:
آزمون اعداد با توان کسری
۱. قاعده تبدیل یک عدد با توان کسری به نماد رادیکال چیست؟
هر عدد به توان m/n معادل ریشه nام آن عدد به توان m است.
عدد با توان کسری را می توان فقط با ریشه دوم جایگزین کرد.
توان کسری فقط برای اعداد منفی قابل تبدیل به رادیکال است.
اعداد با توان کسری امکان تبدیل به رادیکال ندارند.
عبارت «هر عدد به توان m/n معادل ریشه nام آن عدد به توان m است» درست است، زیرا این رابطه دقیقا همان گونه بیان شده که عدد با توان کسری را می توان به صورت رادیکال، یعنی ریشه nام آن عدد (پایه)، نوشت و سپس به توان m رساند.
۲. کدام روش بیان معادل رادیکال مانند به صورت عدد با توان کسری صحیح است؟
رادیکال معادل x به توان ۱ تقسیم بر ۲ است.
رادیکال را به x به توان ۳ تقسیم بر ۲ تبدیل میکنیم.
رادیکال را به x به توان ۲ تقسیم بر ۱ مینویسیم.
رادیکال همان x به توان ۲ تقسیم بر ۳ است.
رادیکال معادل x به توان ۱ تقسیم بر ۲، یعنی ، است.
۳. برای محاسبه ۲ به توان ۳/۲ بدون ماشین حساب، کدام روش صحیح است؟
ابتدا ریشه دوم ۲ را پیدا کرده و سپس آن را به توان ۳ برسانید.
ابتدا عدد ۳ را بر ۲ تقسیم و سپس ۲ را به آن توان برسانید.
ابتدا ۲ را به توان ۳ رسانده و سپس ریشه دوم نتیجه را بگیرید.
فقط کافیست ۲ را با ۳ جمع و سپس تقسیم بر ۲ کنید.
برای محاسبه عبارت ۲ به توان ۳/۲، ابتدا باید ۲ را به توان ۳ رساند که میشود ۸ و سپس ریشه دوم عدد ۸ را محاسبه کرد. روش «ابتدا ۲ را به توان ۳ رسانده و سپس ریشه دوم نتیجه را بگیرید» دقیقا همان تبدیل توان کسری به رادیکال است که در متن توضیح داده شده و معادل یا میشود.
۴. در ضرب پایههای مشابه با توان کسری، چگونه باید نمای جدید را به دست آورد و دلیل درستی این روش چیست؟
جمع کردن نماها برای به دست آوردن نمای جدید صحیح است زیرا توانها با یکدیگر ترکیب میشوند.
تقسیم کردن یکی از نماها بر دیگری، تنها روش درست است زیرا نمای بزرگتر غالب میشود.
ضرب کردن نماها تنها راه بدست آوردن نمای جدید هنگام ضرب اعداد مشابه است.
تفریق نماها به دست آوردن نتیجه ضرب را سادهتر میکند زیرا شباهت پایهها این را ایجاب میکند.
در ضرب پایههای مشابه با توان کسری باید نماها را با هم جمع کرد زیرا طبق قاعده توانها، هنگامی که پایهها یکسان هستند حاصل ضرب آنها برابر با همان پایه به توان مجموع نماها است.
۵. برای محاسبه عددی مانند ۵ به توان -۲/۳، کدام مسیر صحیح است و چرا باید از وارون عدد استفاده شود؟
نمای کسری را به رادیکال تبدیل کرده و سپس وارون نتیجه مثبت را میگیریم.
عدد ۵ را مستقیما به همان صورت به توان ۲/۳ میبریم و علامت منفی را تغییر نمیدهیم.
ابتدا رادیکال را محاسبه نموده و سپس منفی را نادیده میگیریم.
عدد ۵ را به توان مثبت ۲/۳ میرسانیم، سپس به آن یک واحد اضافه میکنیم.
در محاسبه اعدادی با توان کسری منفی مانند «۵ به توان -۲/۳»، باید ابتدا عدد را به توان مثبت یعنی ۲/۳ رساند که همان تبدیل به رادیکال است، سپس وارون نتیجه به دست آمده را محاسبه کرد. در واقع، علامت منفی در توان نشاندهنده گرفتن وارون عدد حاصل از محاسبه توان مثبت است.













درود.ممنونم از توضیحاتتون.
خدا پشت و پنهاهتون و دمتون گرم.
سلام
ببخشید میشه کسر (y/y+1)^3/2 رو بصورت y/y+1^3/2 نوشت ؟؟ (Y در صورت هست و y+1 در مخرج )
سلام متشکرم از تدریس عالیتون
ببخشید اگر یک عدد کسری به توان کسر دیگری برسد چطوری حساب میکنیم مثلا ۳/۲ به توان ۴/۵
اگر اعداد منفی به توان مثبت برسند و در پرانتز باشند (یعنی جواب مثبت در بیاد) منفی از بین میره و میشه.
سلام حاصل (x+y)^۱/۲ چطور میشه
سلام کسی هس که بتونه این سؤالو جواب بده؟
27به توانxبرابر است 1تقسيم بر x
حالxچقدر است؟؟؟؟؟؟؟؟؟
سلام و درود :
اول از همه مرسی بابت این مطلب به شدت روان و عالی اما عذر میخوام استاد من یک سوال اینجا واسم پیش اومد … چطور میتونیم بگیم که اگر توان کسری ای استفاده میکنیم برابر با رادیکاله ؟ یعنی به زبانی ساده تر بخوام سوالم رو بیان کنم اینطور بگم که مثلا اگر میگیم که
۴ به توان نیم چطوری میتونیم به این اثبات برسیم که منظورمون رادیکاله … یعنی اگر رادیکال نباشه راهی هست که بتونیم توان کسری رو حل کنیم؟
سلام عزیزم کلا در ریاضی توان و رادیکال مفهوم برعکس همدیگر را بیان میکنند
با سلام.حاصل این عبارت چجور حساب میشه 〖0.72〗^(1/3)
خیلی خوب ممنون از سایت عالیتون
مچکرم
سلام نگار گرامی.
خوشحالیم که از این آموزش استفاده کردهاید.
شاد و پیروز باشید.
سلام چرا اعداد منفی به توان کسر منفی نمی شوند ؟
سلام.
اعداد منفی به توان کسر میتوانند منفی شوند. چیزی ممکن است رخ دهد. مثلاً عبارت (−8)31 را در نظر بگیرید. حاصل این عبارت اینگونه بهدست میآید:
(−8)31=((−2)3)31=(−2)3×31=(−2)1=−2
شاد و پیروز باشید.
سلام مثلا عددی با توان کسری که رند نیست رو چطوری انجام بدیم بدون ماشین حساب؟مثلا 2به توان3\7 یا 4به توان ¼
سلام.
عدد اعشاری به توان عدد اعشاری بدون ماشین حساب چطور میشه حساب کرد؟!
خداوند خیرتون بده مطالب خیلی خوب بود
سلام آ
آیا اعدا منفی هم می توانند به توان کسیری برسند وای آیا قابل قبول است یا خیر
چون من داخل کتاب درسی مشاهده کردم گفت غیر قابل قبول اما سایتmathway و معلم من می گه مورد قبول است
الان کدام درسته
سلام.
اعداد منفی را میتوان به توان یک عدد کسری (مثبت یا منفی) رساند. البته این موضوع معمولاً در کتابهای درسی با جزئیات بیان نمیشود، زیرا در سطوح بالاتر به آن پرداخته میشود.
شاد و پیروز باشید.
به به به به لذت می برم و کیف می کنم آفرین بر شما
سلام وقت بخیر تو عبارتی که هم بیرون عبارت توان منفی داره و هم داخل عبارت چیکار باید بکنیم؟ مثل این
2- ^(36a^-5÷9a^2) با معکوس کردن داخل عبارت هم علامت توان تغییر میکنه؟
سلام آرای عزیز.
عبارت هرچه پیچیده هم باشد، از همان قواعدی که در متن گفتیم، استفاده میکنیم. در این موردی که نوشتهاید، ابتدا از داخلیترین بخش شروع میکنیم و آن را ساده میکنیم. سپس پرانتزهای بیرونی را ساده خواهیم کرد. بنابراین، ابتدا 36a−5÷9a2 را ساده میکنیم:
$$36a^{-5}÷9a^2 $= \frac {36 a^{-5}}{9 a^2}=\frac {36}9a^{-5-2}= 4a^{-7} $$
سلام.
سپاس از همراهیتان با مجله فرادرس.
شاد و پیروز باشید.
خیلی ممنون از مقاله عالی و مختصرتون من امروز صبح امتحان ریاضی داشتم دیروز اینارو خوندم و امتحانمو خیلی خوب نوشتم خیلی ممنون از مقالتون
سلام طاهای عزیز.
بسیار خوشحالیم که از آموزشهای مجله فرادرس استفاده کردهاید.
به امید موفقیتهای بیشتر.
سلام خواستم خدمتتون بگم که اعداد منفی کلا به توان کسری نمیرسن و تعریف نشده میشن تا اونجایی که میدونم اگه دلیلی دارید خواهشا بگید
اگر اعداد منفی به توان مثبت برسند و در پرانتز باشند (یعنی جواب مثبت در بیاد) منفی از بین میره و میشه.
سلام.
در حالت کلی نمیتوان چنین چیزی گفت. برای مثال، عبارت (−8)32 را در نظر بگیرید که در آن یک عدد منفی به توان کسری رسیده و حاصلش عدد 4 است.
شاد و پیروز باشید.
مثال آخر،چرا بیست تقسیم بر ده رو کردین بیست ضربدر ده؟
سلام.
در این مثال، ابتدا 400−1/2 را از مخرج به صورت آوردهایم که به 4001/2=20 تبدیل شده است. سپس عدد 10001/3=10 را در آن ضرب کردهایم.
موفق باشید.
سلام عالی بود ممنون
میتونم بگم یه نابغه در اموزش این مطلب رو نوشته راحت در کمترین زمان به این مبحث مسلط شدم
سلام.
از پیام محبتآمیز شما بسیار سپاسگزارم.
سالم و سربلند باشید.