پیچش و تنش برشی – به زبان ساده

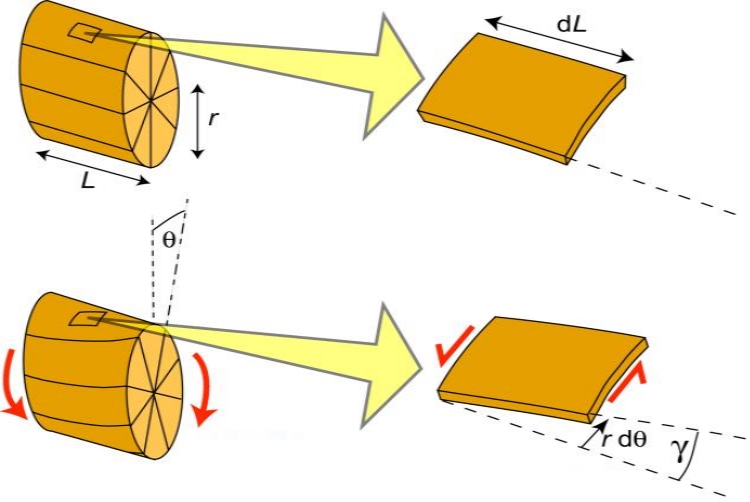
در این مطلب قصد داریم تا مفهوم پیچش و تنش برشی ایجاد شده در نتیجه آن را توضیح دهیم. البته پیشنهاد می‌شود در ابتدا مطالب تنش‌ و تنش برشی و کرنش برشی را مطالعه فرمایید.

پیچش و تنش

به‌منظور توضیح مفهوم پیچش، در ابتدا میله‌ای را همان‌طور که ادامه ارائه شده در نظر بگیرید. مطابق با شکل فرض کنید که نیروی $$F$$ تلاش دارد که میله‌ را در جهت ساعتگرد به حرکت در آورد. توجه داشته باشید که این میله در انتهای دیگرش به دیوار متصل شده است. بنابراین در انتهای دیگرِ میله، نیرویی برابرِ $$F$$ وجود دارد که در تلاش است تا میله را در جهتی عکس دوران دهد.

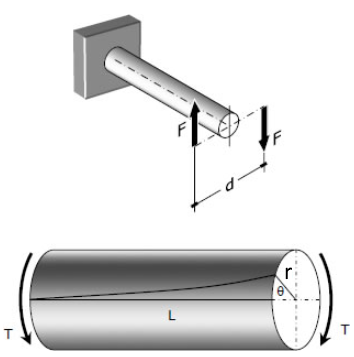
همان‌طور که می‌دانید، تنش برشی را با نماد $$\tau$$ نشان می‌دهند. این صورت اندازه تنش برشی در نتیجه پیچشِ یک میله برابر است با:

$$\large \tau = \dfrac { T \rho } { J }$$

در رابطه فوق، $$T$$، گشتاور پیچشی وارد شده به میله، $$\rho$$، فاصله محل محاسبه تنش از مرکز میله و $$J$$ نشان دهنده گشتاور اینرسی قطبی سطح مقطع میله حول مرکز است. بنابراین برای سطوح‌ مختلف باید گشتاور قطبی مربوط به آن‌ها محاسبه شوند. برای نمونه میله‌ای با سطح مقطع دایره‌ای به قطر $$D$$ را همان‌طور که در ادامه ارائه شده، در نظر بگیرید.

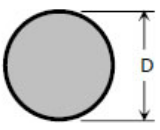
برای مقطع فوق، گشتاور قطبی و تنش برشی ماکزیمم برابرند با:

$$\large J = \dfrac { \pi } { 32 } D ^ 4 \ , \ \tau _ { max } = \dfrac { 16 T }{ \pi D ^ 3 }$$

همین مقادیر برای شکل زیر (استوانه‌‌ای توخالی با قطر خارجیِ $$D$$ و قطر داخلی $$d$$ ) نیز برابرند با:

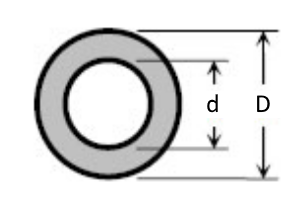
$$\large J = \dfrac { \pi } { 32 } ( D ^ 4 - d ^ 4 ) \ , \ \tau _ { max } = \dfrac { 16 T D } { \pi ( D ^ 4 - d ^ 4 ) }$$

زاویه پیچش

فرض کنید میله‌ای به طول $$L$$ به یک نقطه ساکن (مثلا دیوار) متصل شده و به سر دیگر آن گشتاور پیچشی $$T$$ وارد می‌شود. در این صورت میزان زاویه پیچش در این میله برابر است با:

$$\large \theta = \dfrac { T L } { J G } \, \text {in radians}$$

توجه داشته باشید که در رابطه فوق، $$T$$، گشتاور پیچشی بر حسب $$N . m m$$ و $$G$$ برابر با مدول برشی است که بر حسب $$M P a$$ بیان می‌شود. بنابراین $$L$$ بر حسب $$m m$$ بوده و $$J$$ نیز بر حسب $${ m m } ^ 4$$ در رابطه قرار داده می‌شود. هم‌چنین دقت کنید همان‌طور که در بالا نیز نشان داده شده، زاویه محاسبه شده بر حسب رادیان است.

توان منتقل شده توسط شفت

شفتی که با سرعت زاویه‌ای ثابتِ $$\omega$$ در حال دوران است، گشتاور پیچشی ثابتی برابر با $$T$$ به آن وارد می‌شود. در این صورت توان منتقل شده توسط این شفت برابر است با:

$$\large P = T \omega = 2 \pi T f$$

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

در رابطه فوق $$T$$ برابر با گشتاور بر حسبِ $$N . m$$ و $$f$$ فرکانس نوسان یا تعداد دوران در هر ثانیه است. با توجه به این ابعاد، توانِ $$P$$ نیز بر حسب وات بدست خواهد آمد. به‌منظور درک بهترِ مفاهیمِ ارائه شده در بالا، مثال‌هایی در ادامه طرح شده‌اند که مطالعه آن‌ها می‌توانند در درک مطلب کمک‌کننده باشند.

مثال ۱

شفتی فولادی به طول $$3 \ ft$$، دارای قطری برابر با $$4 \ in$$ است. فرض کنید به این شفت گشتاوری پیچشی برابر با $$15 \ kip·ft$$ وارد شود. در این صورت با فرض این‌که مدول برشی میله برابر با $$G = 12 × 106 \ \ p s i$$ باشد، تنش برشی ماکزیمم و میزان زاویه پیچیده‌شده در میله را بیابید.

تنش برشی ماکزیمم برابر است با:

$$\large \tau _ { m a x } = \dfrac { 16 T } { \pi D ^ 3 } = \dfrac { 16 ( 15 ) ( 1000 ) ( 12 ) } { \pi ( 4 ^ 3 ) }$$

$$\large \tau _ { max } = 14 324 \, \text {psi}$$

در مرحله بعد، میزان زاویه منحرف شده نیز به‌صورت زیر بدست می‌آید:

$$\large \theta = \dfrac { T L } { J G } = \dfrac { 15 ( 3 ) ( 1000 ) ( 1 2^ 2 ) } {\frac { 1 } { 32 } \pi ( 4 ^ 4 ) ( 12 \times 10 ^ 6 ) }$$

$$\large \theta = 0.0215 \, \text {rad}$$

البته می‌توان زاویه پیچش بدست آمده را بر حسب درجه نیز بیان کرد. میزان زاویه پیچش برابر است با:

$$\large \theta = 1.23 ^ \circ$$

مثال فوق نمونه‌ای عادی از نحوه بدست آوردن تنش و کرنش زاویه‌ای بود. در ادامه مثال‌هایی را ارائه خواهیم داد که در آن‌‌ها شفت‌ از چندین بخش تشکیل شده یا این‌که مسئله از جنس انتقال توان باشد.

مثال ۲

شفتی به طولِ $$5 m$$ را در نظر بگیرید که تحت گشتاوری پیچشی به اندازه $$4 ^ \circ$$ پیچیده شده است. با فرض این‌که ماکزیمم تنش برشی ایجاد شده در این شفت برابر با $$80 \ MPa$$ بوده و مدول برشی آن برابر با $$G = 83 \ G P a$$ باشد، میزان توان منتقل شده در هنگام چرخش شفت با فرکانسِ $$20 \ Hz$$ را بدست آورید.

در اولین قدم با استفاده از رابطه بدست آمده برای زاویه، مقدار گشتاور وارد شده به میله بر حسب قطر، مطابق با رابطه زیر بدست خواهد آمد.

$$\large \theta = \dfrac { T L } { J G }$$

$$\large 4 ^ \circ \left ( \dfrac { \pi } {1 8 0 ^\circ} \right ) = \dfrac { T ( 5 )( 1000 ) } { \frac { 1 } { 32 } \pi d ^ 4 ( 83 \, 000 ) }$$

$$\large T = 0.1138 d ^ 4$$

از طرفی می‌توان با استفاده از فرمول تنش ماکزیمم، اندازه قطر را بدست آورد.

$$\large \tau _ { max } = \dfrac { 16 T } { \pi d ^ 3 }$$

$$\large 80 = \dfrac { 16 ( 0.1138 d ^ 4 ) } { \pi d ^ 3 }$$

با بدست آمدن قطر، از رابطه ارائه شده برای محاسبه توان استفاده می‌کنیم و توان را بدست می‌آوریم.

$$\large T = \dfrac { P } { 2 \pi f }$$

$$\large 0.1138 d ^ 4 = \dfrac { P } { 2 \pi ( 20 ) }$$

$$\large P = 14.3 d ^ 4 = 14.3 ( 1384 )$$

$$\large P = 5 \,186 \, 237 \, 285 \, \text {N} \cdot \text {mm/sec}$$

$$\large P = 5 \,186 \, 237.28 \, \text {W}$$

بنابراین نهایتا توان منتقل شده توسط شفت برابر با $$P = 5.19 \, \text { MW}$$ بدست می‌آید.

مثال ۳

شفتی فولادی به قطر $$5 \ m$$ را در نظر بگیرید. چرخ‌دنده‌ای به فاصله‌ $$2 \ m$$ از انتهای سمت چپ، توان $$70 \ kw$$ را به سیستم تحویل می‌دهد و دیگر چرخ‌دنده‌ها مطابق با شکل زیر این توان را مصرف می‌کنند. در این صورت موارد خواسته شده را بدست آورید.

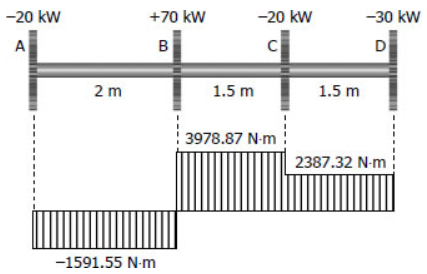
1. ضخامتی یکنواخت از قطر که به ازای آن تنش برشی بیشتر از $$60 \ M P a$$ نشود.
2. اگر ضخامت یکنواخت شفت برابر با $$100 \ m m$$ باشد، میزان زاویه منحرف شده یک سمت از شفت را نسبت به سمت دیگر آن بیابید. مدول برشی را برابر با $$G = 83 G P a$$ در نظر بگیرید.

(a): در ابتدا باید گشتاور تولید شده یا وارد شده به هریک از شفت‌ها را یافت. در حقیقت گشتاور وارد شده یا خارج شده از هریک از شفت‌ها برابرند با:

$$\large T = \dfrac { P } { 2 \pi f }$$

$$\large T _ A = T _ C = \dfrac {-20 ( 1000 ) } { 2 \pi ( 2 ) } = -1591.55 \, \text {N} \cdot \text {m}$$

$$\large T _ B = \dfrac { 70 ( 1000 ) } { 2 \pi ( 2 ) } = 5570.42 \, \text {N} \cdot \text {m}$$

$$\large T _ D = \dfrac { -30 ( 1000 ) } { 2 \pi ( 2 ) } = -2387 . 32 \, \text { N } \cdot\text {m}$$

به منظور بدست آوردن قطر، می‌توان از رابطه تنش برشی ماکزیمم استفاده کرده و آن را در هریک از مقاطع بدست آورد.

برای قسمت AB:

$$60 = \dfrac { 16 ( 1591 . 5 5 ) ( 1000 ) } { \pi d ^ 3 }$$

$$d = 51 . 3 \, \text {mm}$$

برای قسمت BC:

$$60 = \dfrac { 16 (3978.87) ( 1000 ) } { \pi d ^ 3 }$$

$$d = 69.6 \, \text {mm}$$

برای قسمت CD:

$$\large 60 = \dfrac { 16 ( 2387 . 32 ) ( 1000 ) } { \pi d ^ 3 }$$

$$\large d = 58.7 \, \text {mm}$$

ما می‌خواهیم قطر شفت، در تمامی قسمت‌ها عددی یکنواخت باشد؛ بنابراین از میان مقادیر فوق باید ماکزیمم مقدار را در نظر گرفت. ماکزیمم مقدار قطر مربوط به قسمت BC است. بنابراین قطر یکنواخت شفت برابر است با:

$$\large d=69.6 \ \ mm$$

(b): میزان زاویه منحرف شده در یک بخش از شفت را می‌توان با استفاده از اختلاف گشتاور دو سر آن بدست آورد. بنابراین میزان اختلاف نقطه D نسبت به A برابر است با:

$$\large \theta _ { D / A } = \dfrac { 1 } { J G } \Sigma T L$$

در نتیجه نهایتا پیچش نسبی دو سر شفت، برابر می‌شود با:

$$\large \theta _ {D / A } = \dfrac { 1 } { \frac { 1 } { 32 } \pi ( 100 ^ 4 )( 83 \, 000 ) } \, [ \, -1591.55 ( 2 ) + 3978.87 ( 1.5 ) + 2387.32 ( 1.5 ) \, ] \, ( 1000 ^ 2 )$$

$$\theta _ { D / A } = 0 . 0 0 7 \, 8 1 3 \, \text {rad}$$

مثال ۴

مطابق با شکل زیر شفتی فولادی را در نظر بگیرید که با فرکانس $$4 \ Hz$$ دوران می‌کند. گشتاور $$35 kW$$ از نقطه $$A$$ گرفته می‌شود. هم‌چنین $$20 kW$$ از نقطه $$B$$ گرفته می‌شود. از طرفی از نقطه $$C$$ مقدارِ $$55 Kw$$ اعمال می‌شود. با توجه به این توصیفات بیشترین میزان تنش برشی و همچنین بیشترین میزان انحراف زاویه‌ای نقطه $$A$$ نسبت به $$C$$ را بدست آورید.

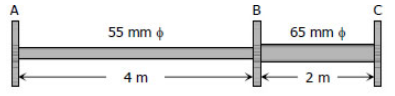
در هریک از نقاط شفت مقداری از توان وارد یا خارج می‌شود. بنابراین در هریک از نقاط شفت مقداری گشتاور اعمال شده یا از شفت گرفته شده است. به‌منظور بدست آوردن مقدار گشتاور، کافی است از رابطه بین گشتاور و توان استفاده کرد. نهایتا گشتاور در هریک از نقاطِ شفت برابر می‌شود با:

$$\large T _ A = \dfrac { -35 ( 1000 ) } { 2 \pi ( 4 ) } = -1392.6 \, \text{ N} \cdot \text {m}$$

$$\large T _ B = \dfrac { -2 0 ( 1000 ) } { 2 \pi ( 4 ) } = -795 . 8 \, \text{N} \cdot \text {m}$$

$$\large T _ C = \dfrac { 55 ( 1000 ) } { 2 \pi ( 4 ) } = 2188.4 \, \text {N} \cdot \text {m}$$

شکل زیر نحوه اعمال شدن گشتاور‌ها به نقاط مختلف شفت را نشان می‌دهد.

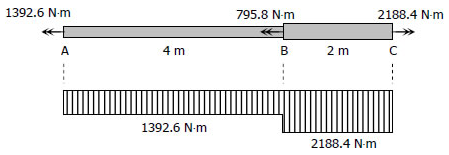
با توجه به گشتاور‌های بدست آمده، تنش در نقاط مختلف شفت به‌صورت زیر بدست می‌آیند.

$$\large \tau _ { max } = \dfrac { 16 T } { \pi d ^ 3 }$$

$$\large \tau _ { A B } = \dfrac { 16 ( 1392.6 ) ( 1000 ) } { \pi ( 55 ^ 3 ) } = 42.63 \, \text { MPa}$$

$$\large \tau _ { B C } = \dfrac { 16 ( 2188.4 ) ( 1000 ) } { \pi ( 65 ^ 3 ) } = 40.58 \, \text { MPa }$$

بنابراین بیشترین تنش در شفت برابر با $$\tau _ { ma x } = \tau _ { A B }= 42.63 \, \text { MPa}$$ است. مقدار زاویه منحرف شده نیز مشابه با مثال قبل برابر با برآیند انحرافِ ناشی از تمامی گشتاور‌ها بدست می‌آیند.

$$\large \theta = \dfrac { T L } { J G }$$

$$\large \theta _ { A / C } = \dfrac { 1 } { G } { \Large \Sigma } \dfrac { T L }{ J }$$

$$\large \theta _ { A / C } = \dfrac { 1 } { 8 3 \, 000 } \left[ \dfrac {1392.6 ( 4) } { \frac{ 1 } { 32 } \pi ( 55 ^ 4 ) } + \dfrac { 2188.4 ( 2 ) } { \frac { 1 }{ 3 2 } \pi (65^4)} \right]\,(1000 ^ 2 )$$

$$\large \theta _ { A / C } = 0.104 \,796\,585 \, \text {rad}$$

توجه داشته باشید که در برخی از موارد ممکن نیروی برشی نیز به تیر وارد شود که در این موارد باید تاثیر تمامی نیرو‌های برشی در نظر گرفته شوند. در مطالب آینده، بیشتر در این مورد بحث خواهیم کرد.

^^