معیارهای مکانی و گشتاورها در علم داده – راهنمای کاربردی
این نوشتار قسمت سوم از مطالب دنبالهدار در مورد نقش آمار در حوزه علم داده است که به موضوع و مبحث معیارهای مکانی و گشتاورها میپردازد. البته برای نمایش این مقادیر و شاخصها از نمودارهایی نیز کمک خواهیم گرفت.


برای آشنایی با انواع توزیعهای احتمالی مطلب توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس را بخوانید. همچنین به منظور آشنایی با نحوه ترسیم نمودار جعبهای که در این متن به آن اشاره خواهیم داشت به نوشتار نمودار جعبه ای (Boxplot) و رسم آن در پایتون – به زبان ساده مراجعه کنید. قسمتهای مختلف این دنباله مقالات مطابق با فهرست زیر هستند.
- قسمت اول: شاخصهای آمار توصیفی در علم داده — راهنمای کاربردی
- قسمت دوم: توزیع های آماری مهم در علم داده — راهنمای کاربردی
- قسمت سوم: معیارهای مکانی و گشتاورها در علم داده — راهنمای کاربردی
- قسمت چهارم: وابستگی- کوواریانس و ضریب همبستگی --- راهنمای کاربردی
- قسمت پنجم: احتمال شرطی، قضیه بیز (Bayes's Theorem) --- راهنمای کاربردی
معیارهای مکانی و گشتاورها
همانطور که میبینید باز هم سعی داریم، رفتار دادهها را به شکلی مناسب، توصیف کنیم. به این ترتیب مشخص است که هدف، آشنایی با ساختار دادهها است. در قسمتهای اول، دوم و سوم، به ویژگیها و خصوصیات یک متغیر میپردازیم ولی در قسمتهای چهارم و پنجم تاثیرپذیری یا کنش و واکنش دو متغیر یا دو سری دادهها را مورد بررسی قرار خواهیم داد.
معیارهای مکانی (Measures of Location)
در نوشتارهای قبلی این سری مطالب با معیارهای مرکزی در آمار توصیفی مثل میانگین و میانه آشنا شدید. در اینجا به بررسی شاخصهای دیگری میپردازیم که به عنوان «معیارهای مکانی» (Measures of Location) معروف هستند.
صدکها (Percentiles)
اگر دادهها را از کوچک به بزرگ مرتب کنیم، نقاطی که آنها را به صد قسمت تقسیم کنند، صدک نامیده میشوند. در حقیقت یک صدک، مقداری است که درصد خاصی از مشاهدات از آن کمتر هستند.
برای مثال اگر صدک پنجاهم را در نظر بگیریم، میزان درصد برابر است با ۵۰٪، پس باید به دنبال مقداری باشیم که ۵۰٪ مشاهدات (در صورتی که عمل مرتبسازی صورت گرفته باشد) از آن کمتر هستند. با توجه به تعریفی که در قسمت اول تحت عنوان معیارهای مرکزی داشتیم مشخص است که این مقدار باید میانه باشد. پس میانه همان صدک پنجاهم است.
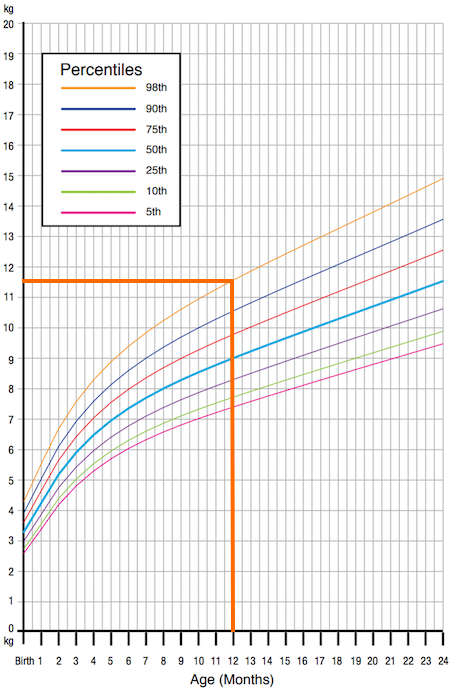
برای مثال، نمودار رشد نوزادان و کودکان زیر دو سال را در نظر بگیرید. با دنبال کردن خطوط نمودار مشخص میشود که 98٪ بچههای ۱۲ ماهه، وزنی کمتر از 11.5 کیلوگرم دارند. پس 11.5 کیلوگرم، صدک 98ام برای وزن کودکان یکساله است.
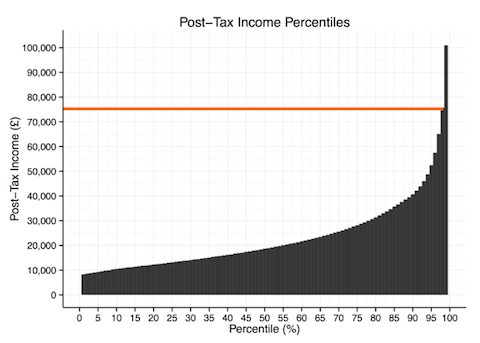
به عنوان یک مثال دیگر، توزیع درآمدها را در نظر بگیرید. بوسیله نمودار زیر مشخص است که 75000 پوند در انگلستان، صدک ۹۹ام است. یعنی ۹۹٪ از افراد جامعه درآمدی کمتر از این مقدار دارند و فقط ۱٪ هستند که در سال درآمدی بیش از 75000 پوند دارند.
با توجه به تعریفی که برای صدکها ارائه شد، میتوان معیارهای مکانی دیگر مانند چارک و دهک را نیز معرفی کرد. مشخص است که منظور از چارکها، نقاطی است که دادهها را به چهار قسمت تقسیم میکنند. همچنین دهکها نیز براساس ۹ نقطه، دادهها را به ده قسمت مساوی تقسیم میکنند. در این حالت به صورت کلی به این معیارهای مکانی «چندکها» (Quantiles) میگویند.
نکته: برای تقسیم دادهها به چهار قسمت، به سه نقطه احتیاج است. پس مشخص است که سه نقطه به عنوان چارک اول، دوم و سوم داریم. همین رابطه را هم برای دهکها و صدکها میتوان در نظر گرفت. به این ترتیب تعداد دهکها، برابر با نه نقطه و تعداد صدکها نیز برابر با ۹۹ نقطه است.
چارک اول را با Q1 و چارک دوم (میانه) را با Q2 و در آخر چارک سوم را نیز با Q3 نشان میدهند. دهکها نیز به صورت D1 تا D9 نامگذاری شدهاند. همچنین صدک اول تا صدک ۹۹ام را با P1 الی P99 مشخص میکنند.
دامنه میان چارکی (Interquartile Range)
دامنه میان چارکی (Interquartile Range) که به اختصار IQR نامیده میشود، به عنوان معیاری برای نشان دادن فاصله بین چارک اول و سوم است.
معمولا براساس این شاخص یا معیار، شناسایی دادههای پرت صورت میگیرد. در نمودارهای جعبهای (Boxplot)، چارکها رسم شده و فاصله بین چارک اول و سوم، را به عنوان طول جعبه در این نمودار نظر میگیرند.
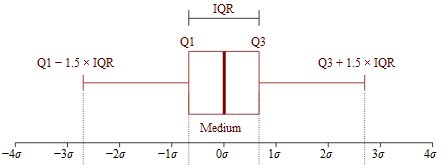
مشخص است ۵۰٪ دادهها باید بین چارک اول و سوم قرار بگیرند. همچنین نقاطی که بیش از 1.5 برابر دامنه میان چارکی از چارک اول یا سوم فاصله داشته باشند، نقاط پرت (Outlier) یا دورافتاده نامیده میشوند.
نمودار جعبهای (Boxplot)
یک روش استاندارد برای نمایش توزیع دادهها، رسم «نمودار جعبهای» (Boxplot) است. این نمودار براساس شاخصهای آماری مانند «کوچکترین مقدار» (Minimum)، «چارک اول» (First Quartile -Q1)، «میانه» (Median)، «چارک سوم» (Third Quartile- Q3) و «بزرگترین مقدار» (Maximum) ترسیم میشود.
همانطور که در تصویر زیر مشاهده میکنید، این نمودار به توصیف ویژگیها زیر برای دادهها میپردازد.
- نمایش نقاط تمرکز دادهها (میانه و معیارها یا اندازههای مکانی مانند چارک اول و سوم)
- دامنه تغییرات برای دادهها که توسط فاصله بین بزرگترین (Upper whisker) و کوچکترین نقطه (Lower whisker) حاصل میشود.
- نمایش نقاط پرت، براساس ضریبی از دامنه میان چارکی نسبت به چارک اول و سوم
- نمایش تقارن در توزیع دادهها، در صورتی که میانه درست در وسط جعبه قرار گیرد.
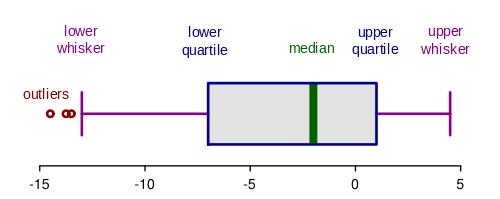
در نمودار بالا مقدار فاصله بین بزرگترین داده و کوچکترین داده تقریبا حدود ۲۰ است () ولی از آنجایی که سه نقطه ابتدایی بیش از یک و نیم برابر طول جعبه از چارک اول فاصله دارند، آنها را به عنوان نقاط پرت محسوب کرده و چهارمین عددی که از بقیه دادهها کوچکتر است به عنوان محل شروع نمودار (lower whisker) در نظر گرفته شده است.
در تصویر زیر مقایسهای بین درصدهایی که در نمودار جعبهای و نمودار فراوانی توزیع نرمال وجود دارد، صورت گرفته است. مشخص است که در نمودار جعبهای، فاصلهها برحسب چارکها هستند در حالیکه در نمودار فراوانی توزیع نرمال، فاصله برمبنای انحراف استاندارد سنجیده میشود.
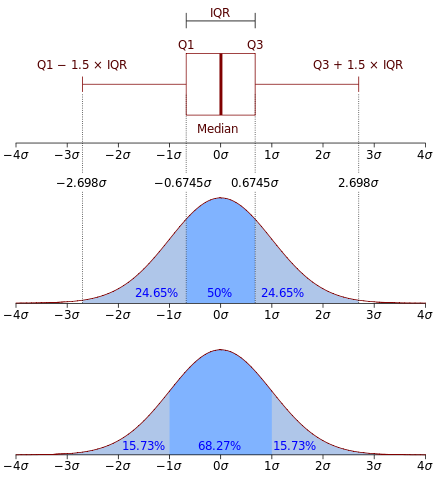
پس مشخص است که برمبنای فاصله در نمودار جعبهای، ۵۰ درصد دادهها در دامنه میان چارکی قرار دارند در حالیکه در فاصله یک انحراف استاندارد از میانگین 68.27٪ دادهها قرار میگیرند.
همچنین با توجه به توزیع نرمال، مقادیری که بیش از سه برابر انحراف استاندارد از میانگین دور باشند، احتمال مشاهده کمی دارند و معمولا آنها را به عنوان داده پرت در نظر میگیرند در حالیکه با توجه به نمودار جعبهای این محدوده کمی بزرگتر است. یعنی ممکن است دادههایی که بیش 2.698 برابر انحراف استاندارد از میانگین فاصله داشته باشند، توسط نمودار جعبهای به عنوان دادهپرت در نظر گرفته شوند.
گشتاورها (Moments)
«گشتاورها» (Moments) میتوانند به مشخص کردن رفتار دادهها از نظر شکل توزیع یا تقارن کمک کنند. در این قسمت با این معیارها آشنا خواهیم شد.
به طور کلی شیوه محاسبه گشتاورها به صورت زیر است. معمولا گشتاورهای را با حرف نشان میدهند که در آن نشان دهنده مرتبه گشتاور است.
به این ترتیب برای اساس مقدارهای مختلف میتوان گشتاورهای مختلفی را تعریف و مشخص کرد. در ادامه به معرفی آنها میپردازیم.
- گشتاور اول- : همانطور که قابل مشاهده است، اگر در رابطه بالا مقدار باشد، گشتاور اول، بیانگر میانگین خواهد بود. به این ترتیب میانگین «گشتاور اول» (First Moment) محسوب میشود.
- گشتاور دوم- : به کمک «گشتاور مرتبه دوم» میتوان واریانس را به عنوان معیار پارکندگی محاسبه کرد. به این منظور کافی است که گشتاور دوم را از مربع گشتاور اول کم کنیم تا واریانس حاصل شود.
- گشتاور سوم- : براساس «گشتاور مرتبه سوم»، چولگی (Skewness) که معیاری برای سنجش تقارن توزیع محسوب میشود، قابل محاسبه است. اگر مقدار چولگی مثبت باشد، منحنی توزیع را چوله به راست میگویند. همچنین زمانی که منحنی توزیع به چپ تمایل داشته باشد، منحنی را چوله با چپ میگویند. در مطالب قبلی فرادرس با عنوان چولگی — تعاریف و شیوه محاسبه با شیوه محاسبه چولگی آشنا شدهاید.
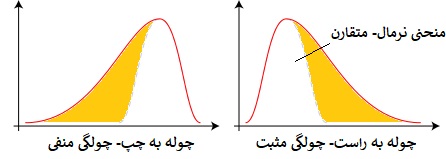
- گشتاور چهارم- : برای محاسبه معیار کشیدگی توزیع (Kurotsis) از گشتاور چهارم استفاده میشود. اگر مقدار کشیدگی بزرگ باشد، منحنی توزیع را برجسته میگویند. همچنین زمانی که منحنی توزیع دارای کشیدگی کوچ باشد، منحنی را پخ مینامند.
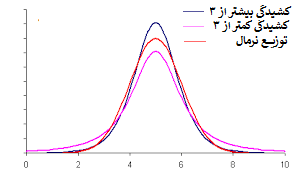
زمانی که میزان کشیدگی بزرگ باشد، احتمال مشاهده مقادیر پرت کم است، در حالیکه کوچک بودن این شاخص، بیانگر احتمال بیشتر برای مشاهده دادهها پرت است. به منظور اطلاع از شیوه محاسبه شاخص کشیدگی بهتر است مطلب کشیدگی — تعریف و شیوه محاسبه را مطالعه کنید.
گشتاورهای مرکزی (Central Moments)
گاهی لازم است در شیوه محاسبه گشتاورها، تغییراتی بوجود آید. برای مثال با توجه به تعریف واریانس که بصورت «میانگین مربعات انحراف از میانگین» بیان میشود، احتیاج به گشتاوری مرکزی است. همانطور که در بخش گشتاورها خواندید، گشتاور دوم برای محاسبه واریانس به کار میآید ولی به تنهایی واریانس نیست. اگر شیوه محاسبه را به صورت زیر درآوریم، گشتاورهای مرکزی مرتبه پدید میآیند.
با توجه به این تعریف، مشخص است که واریانس، «گشتاور مرکزی دوم» خواهد بود. البته باید توجه داشت که گشتاورهای مرکزی فرد با توجه به مفهوم میانگین همگی صفر هستند.
خلاصه و جمعبندی
همانطور که در این نوشتار خواندید، معیار و اندازههای مکانی، در درک رفتار دادهها، موثر هستند. روشهای تشخیص دادههای پرت و همچنین سنجش میزان پراکندگی و خارج بودن از حالت تقارن، به کمک رسم نمودارها و محاسبه گشتاورها امکانپذیر است. به این ترتیب با محاسبه این شاخصها، بهتر میتوانیم تغییرات دادهها را درک کنیم و از دادهها، اطلاعات قابل درک بسازیم. همچنین رسم نمودارهایی مانند نمودار جعبهای و همچنین نمودار فراوانی در نحوه نمایش این رفتارها، بسیار موثر است.
اگر مطلب بالا برای شما مفید بوده است، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزش های SPSS
- مجموعه آموزش های Minitab
- مقایسه معیارهای تمرکز (میانگین، میانه، نما)
- واریانس و اندازههای پراکندگی — به زبان ساده
- چولگی — تعاریف و شیوه محاسبه
- کشیدگی — تعریف و شیوه محاسبه
^^












