مشتق رادیکال با فرجه ۳ و فرجه های دیگر – به زبان ساده

مشتق رادیکال با فرجه ۳ و فرجه های دیگر، معمولا با استفاده از فرمول مشتقگیری زنجیرهای به دست میآید. البته اگر توابع رادیکالی را به صورت توانی بازنویسی کنیم، امکان مشتقگیری از آنها توسط فرمولهای مربوط به مشتق توابع تواندار نیز فراهم میشود. علاوه بر این، مشتق توابع رادیکالی، فرمولهای مخصوص به خود را دارند که در صورت حفظ کردن آنها، دیگری نیازی به روشهای طولانی و پیچیده نخواهید داشت. در این مطلب از مجله فرادرس، نحوه تعیین مشتق رادیکال با فرجه ۳ و فرجه های دیگر را به همراه حل چندین مثال و تمرین متنوع آموزش میدهیم.
مشتق چیست و چگونه بدست می آید؟
قبل از اینکه نحوه تعیین مشتق رادیکال با فرجه ۳ و فرجه های دیگر را آموزش دهیم، بهتر است یک بار، مفهوم مشتق و روشهای به دست آوردن آن را مرور کنیم. «مشتق» (Derivative)، یک مفهوم ریاضی است که نحوه تغییرات یک تابع را بر اساس تغییرات ورودیهای آن نمایش میدهد.
بر اساس یک تعریف دیگر، مشتق، شیب منحنی تابع در یک نقطه مشخص است. روشهای متعددی برای به دست آوردن مشتق وجود دارد. فرمول کلی این مفهوم ریاضی به صورت زیر نوشته میشود:
$$
\lim _ { \Delta x \rightarrow ۰ } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x }
$$
$$ \Delta x $$، تغییرات جزئی متغیر ورودی $$ x $$ است. علاوه بر رابطه کلی بالا، انواع توابع در ریاضی، فرمولهای مشتق مخصوص خود را دارند.

مشتق رادیکال چیست و چگونه بدست می آید؟
توابع رادیکالی، یکی از انواع تابع در ریاضی هستند که با علامت رادیکال نمایش داده میشوند و برعکس توان توانی عمل میکنند. ساختار کلی رادیکال به صورت زیر است:
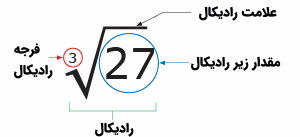
در توابع رادیکالی، به جای مقدار عددی، یک متغیر زیر رادیکال قرار میگیرد. به عنوان مثال، تابع زیر، یک تابع رادیکالی با فرجه m است:
$$
f ( x ) = \sqrt [ m ] {x}
$$
مشتق تابع رادیکالی بالا، با استفاده از فرمول زیر به دست میآید:
$$ \large { f’ \left ( x \right ) } = { \left ( { \sqrt [ \large m \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { m \sqrt [ \large m \normalsize ] { { { x ^ { m – ۱ } } } } } } . } $$
بر اساس این فرمول، اگر $$ m = ۲ $$، مشتق $$ f ( x ) = \sqrt [ m ] {x} $$ برابر خواهد بود با:
$$ \large { f’ \left ( x \right ) } = { \left ( { \sqrt x } \right ) ^ \prime } = { \frac { ۱ } { { ۲ \sqrt x } } . } $$
مثال ۱: مشتق رادیکال x با فرجه ۳
مشتق تابع $$ f ( x ) = \sqrt [ ۳ ] {x} $$ را تعیین کنید.
تابع $$ f ( x ) $$، یک تابع رادیکالی با فرجه ۳ است. برای تعیین مشتق این تابع، میتوانیم از رابطه زیر استفاده کنیم:
$$
\large { f’ \left ( x \right ) } = { \left ( { \sqrt [ \large m \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { m \sqrt [ \large m \normalsize ] { { { x ^ { m – ۱ } } } } } } }
$$
به جای $$ m $$ در رابطه بالا، عدد ۳ را قرار میدهیم:
$$
\large { f’ \left ( x \right ) } = { \left ( { \sqrt [ \large ۳ \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۳ – ۱ } } } } } } . }
$$
به این ترتیب، داریم:
$$
\large { f’ \left ( x \right ) } = { \left ( { \sqrt [ \large ۳ \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۲ } } } } } } }
$$
در نتیجه، مشتق تابع مشتق رادیکال x با فرجه ۳ برابر با $$ { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۲ } } } } } } }$$ است.
مشتق توابع رادیکالی با فرجه ۳
در بخش قبلی، مشتق تابع رادیکال x با فرجه ۳ را به دست آوردیم. اگر عبارت زیر رادیکال، یک تابع باشد، روش به دست آوردن مشتق تابع تغییر میکند. به عنوان مثال، تابع زیر را در نظر بگیرید:
$$ F ( x ) = \sqrt [ ۳ ] { x ^ ۲ } $$
$$ F ( x ) $$، یک تابع رادیکالی با فرجه ۳ است. برخلاف مثال ۱، عبارت زیر رادیکال، یک تابع توانی است. بنابراین، برای به دست آوردن مشتق $$ F ( x ) $$، نمیتوانیم از فرمول معرفی شده در بخش قبلی استفاده کنیم. روشهای مختلفی برای تعیین مشتق تابع بالا وجود دارند که از متداولترین آنها میتوان به قاعده مشتقگیری زنجیرهای و مشتقگیری توانی اشاره کرد.
قاعده مشتقگیری زنجیرهای، برای توابع تو در تو مورد استفاده قرار میگیرد. بر اساس این قاعده، اگر $$ F ( x ) = f ( g ( x ) ) $$ باشد، مشتق $$ F ( x ) $$ برابر خواهد بود با:
$$
F ' ( x ) = \frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
بر اساس این رابطه و پارامترهای تابعی که مثال زدیم، میتوانیم تغییر متغیرهای زیر را در نظر بگیریم:
$$ f ( x ) = \sqrt [ ۳ ] { x } $$
$$ g ( x ) = x ^ ۲ $$
به این ترتیب، داریم:
$$
f ' ( x ) = { \left ( { \sqrt [ \large ۳ \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۲ } } } } } } }
$$
$$
f ' ( g ( x ) ) = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { \left ( x ^ ۲ \right ) ^ { ۲ } } } } } } }
$$
$$
g ' ( x ) = { \left ( x ^ ۲ \right ) ^ \prime } = ۲ x
$$
در نتیجه:
$$
F ' ( x ) = f' [ g ( x ) ] g' (x ) = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { \left ( x ^ ۲ \right ) ^ { ۲ } } } } } } } \cdot ۲ x
$$
$$
F ' ( x ) = f' [ g ( x ) ] g' (x ) = { \frac { ۲ x } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ ۴ } } } } } }
$$
برای سادهسازی جواب بالا میتوانیم عبارت رادیکالی را به صورت عبارت دارای توان کسری بنویسیم:
$$
F ' ( x ) = { \frac { ۲ x } { { ۳ x ^ { \frac { ۴ } { ۳ } } } } }
$$
$$
F ' ( x ) = { \frac { ۲ } { { ۳ x ^ { \frac { ۱ } { ۳ } } } } }
$$
یا
$$
F ' ( x ) = { \frac { ۲ } { { ۳ \sqrt [۳] {x} } } }
$$

به این ترتیب، مشتق یک تابع رادیکالی تو در تو با فرجه ۳ را به روش مشتقگیری زنجیرهای به دست آوردیم. مشتقگیری زنجیرهای، در برخی از موارد، پیچیده و زمانبر میشود. در این موارد، میتوانیم از یک روش سادهتر، یعنی مشتق عبارتهای تواندار استفاده کنیم. فرمول عبارتهای تواندار به صورت زیر نوشته میشود:
$$ \frac { d } { d x } x ^ n = n x ^ { n - ۱ } $$
اکنون، تابع $$ F ( x ) $$ را در نظر بگیرید:
$$ F ( x ) = \sqrt [ ۳ ] { x ^ ۲ } $$
برای استفاده از فرمول مشتق عبارتهای تواندار، تابع $$ F ( x ) $$ را به صورت زیر بازنویسی میکنیم:
$$
F ( x ) = \sqrt [ ۳ ] { x ^ ۲ } = x ^ {\frac { ۲ } { ۳ } }
$$
بر اساس فرمول مشتق توانی، داریم:
$$ n = \frac { ۲ } { ۳ } $$
$$
F ' ( x ) = \left ( x ^ {\frac { ۲ } { ۳ } } \right ) ' = \frac { ۲ }{ ۳ } x ^ { \left ( \frac { ۲ }{ ۳ } - ۱ \right ) }
$$
$$
F ' ( x ) = \frac { ۲ }{ ۳ } x ^ { - \frac { ۱ }{ ۳ } }
$$
$$
F ' ( x ) = \frac { ۲ } { ۳ x ^ { \frac { ۱ }{ ۳ } } }
$$
$$
F ' ( x ) = { \frac { ۲ } { { ۳ \sqrt [۳] {x} } } }
$$
همانطور که مشاهده کردید، برخلاف روش مشتقگیری زنجیرهای، در این روش، نیازی به انجام محاسبه چندین مشتق نبود.
مثال ۲: محاسبه مشتق تابع مثلثاتی رادیکالی با فرجه ۳
مشتق تابع زیر را به دست بیاورید:
$$ F ( x ) = \sqrt [ ۳ ] { \cos \left ( x ^ ۲ \right ) } $$
تابع بالا، یک تابع رادیکالی با یک تابع کسینوس در زیر رادیکال است. به عبارت دیگر، تابع $$ F ( x ) $$، یک تابع تو در تو در نظر محسوب میشود. مشتقگیری از توابع تو در تو، معمولا توسط قاعده مشتقگیری زنجیرهای صورت میگیرد. بر اساس این قاعده، داریم:
$$
F ' ( x ) = \frac { d } { d x } f [ g ( x ) ] =f' [ g ( x ) ] g' (x )
$$
به منظور استفاده از رابطه بالا، توابع $$ f ( x ) $$ و $$ g ( x ) $$ را به صورت زیر در نظر میگیرم:
$$ f ( x ) = \sqrt [ ۳ ] { x } $$
$$ g ( x ) = \cos \left ( x ^ ۲ \right ) $$
مشتق $$ \sqrt [ ۳ ] { x } $$ را در بخشهای قبلی معرفی کردیم. این مشتق برابر است با:
$$
f ' ( x ) = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۲ } } } } } } }
$$
مشتق کسینوس x به توان ۲، با استفاده از قواعد مشتقگیری از توابع مثلثاتی و مشتقگیری زنجیرهای تعیین میشود. این مشتق برابر است با:
$$
g ' ( x ) = - ۲ x \sin \left ( x ^ ۲ \right )
$$
به این ترتیب، داریم:
$$
f ' ( g ( x ) ) = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { \cos ^ { ۲ } \left ( x ^ ۲ \right ) } } } } } }
$$
مشتقهای بالا را درون فرمول مشتقگیری زنجیرهای قرار میدهیم:
$$
F ' ( x ) = f' [ g ( x ) ] g' (x ) = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { \cos ^ { ۲ } \left ( x ^ ۲ \right ) } } } } } } \times - ۲ x \sin \left ( x ^ ۲ \right )
$$
$$
F ' ( x ) = - { \frac { ۲ x \sin \left ( x ^ ۲ \right ) } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { \cos ^ { ۲ } \left ( x ^ ۲ \right ) } } } } } }
$$

مشتق توابع رادیکالی با فرجه های بالاتر از ۳
روشهای به دست آوردن مشتق تابع رادیکال با فرجه های بالاتر از ۳، تفاوتی با روش به دست آوردن مشتق تابع رادیکال با فرجه ۳ ندارد. در فرجههای بالاتر نیز میتوان با استفاده از قاعده مشتقگیری زنجیرهای یا مشتق عبارتهای تواندار و ترکیب آنها با فرمولهای مخصوص مشتقگیری از انواع توابع، به جواب رسید.
البته، یک فرمول کلی برای مشتق تابع رادیکال با فرجه ۳ و فرجه های بالاتر وجود دارد که از قاعده مشتق زنجیرهای گرفته شده است. این فرمول به صورت زیر نوشته میشود:
$$
\frac { d } { d x } \left ( \sqrt [ n ] { u ^ m ( x ) } \right ) = \frac { m \times u ^ { \prime } ( x ) }{ n \sqrt [ n ] { u ^ { n - m } ( x )}}
$$
مثال ۳: تعیین مشتق تابع رادیکالی با فرجه ۴
مشتق تابع زیر را تعیین کنید:
$$
F ( x ) = \left ( x ^ ۲ - ۱ \right ) \left ( \sqrt [ ۴ ] { x } \right )
$$
تابع بالا، حاصلضرب یک تابع چندجملهای در یک تابع رادیکال با فرجه ۴ است. برای به دست آوردن مشتق این تابع، از رابطه مشتق ضرب توابع استفاده میکنیم. این رابطه به صورت زیر نوشته میشود:
$$
\frac { d } { d x } [ f ( x ) g ( x ) ] = f ( x ) g' ( x ) + g ( x ) f' ( x )
$$
تابع چندجملهای را برابر با $$ f ( x ) $$ و تابع رادیکال را برابر با $$ g ( x ) $$ در نظر میگیریم:
$$ f ( x ) = \left ( x ^ ۲ - ۱ \right ) $$
$$ g ( x ) = \left ( \sqrt [ ۴ ] { x } \right ) $$
در مرحله بعد، مشتق هر یک از این توابع را به دست میآوریم. مشتق تابع چندجملهای $$ f ( x ) $$ برابر است با:
$$
f ' ( x ) = \frac { d } { d x } \left ( x ^ ۲ - ۱ \right ) = ۲ x
$$
برای به دست آوردن مشتق تابع رادیکالی $$ g ( x ) $$، از رابطه زیر استفاده میکنیم:
$$
{ \left ( { \sqrt [ \large m \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { m \sqrt [ \large m \normalsize ] { { { x ^ { m – ۱ } } } } } } }
$$
$$
\large { g ’ \left ( x \right ) } = { \frac { ۱ } { { ۴ \sqrt [ \large ۴ \normalsize ] { { { x ^ { ۴ – ۱ } } } } } } }
$$
$$
\large { g ’ \left ( x \right ) } = { \frac { ۱ } { { ۴ \sqrt [ \large ۴ \normalsize ] { { { x ^ { ۳ } } } } } } }
$$
اکنون، توابع $$ f ( x ) $$ و $$ g ( x ) $$ را به همراه مشتقهایشان درون رابطه مشتق ضرب توابع قرار میدهیم:
$$
\frac { d } { d x } \left [ \left ( x ^ ۲ - ۱ \right ) \left ( \sqrt [ ۴ ] { x } \right ) \right ] = \left ( x ^ ۲ - ۱ \right ) { \frac { ۱ } { { ۴ \sqrt [ \large ۴ \normalsize ] { { { x ^ { ۳ } } } } } } } + \left ( \sqrt [ ۴ ] { x } \right ) ۲x
$$
از عبارتهای بالا مخرج مشترک میگیریم و فرم ساده شده آنها را مینویسیم:
$$
\frac { d } { d x } \left [ \left ( x ^ ۲ - ۱ \right ) \left ( \sqrt [ ۴ ] { x } \right ) \right ] ={ \frac { ۹ x ^۲ - ۱ } { { ۴ \sqrt [ \large ۴ \normalsize ] { { { x ^ { ۳ } } } } } } }
$$

حل تمرین مشتق رادیکالی با فرجه ۳ و فرجه های بالاتر
در این بخش، به منظور یادگیری بهتر مبحث مشتق رادیکال با فرجه ۳ و فرجه های بالاتر، به حل چندین تمرین متنوع میپردازیم. در هر تمرین، برخی از فرمولهای مهم مشتق را نیز معرفی میکنیم.
تمرین ۱: تعیین مشتق تقسیم تابع رادیکال با فرجه ۳ بر تابع رادیکال با فرجه ۲
مشتق تابع $$ \frac { \sqrt [۳] { x } }{ \sqrt { x }} $$ را به دست بیاورید.
تابع مورد سوال، یک تابع کسری را نشان میدهد از صورت و مخرج آن از دو تابع با فرجههای متفاوت تشکیل شدهاند. برای به دست آوردن مشتق این تابع، دو روش کلی وجود دارد که در ادامه، هر یک از آنها را توضیح میدهیم.
مشتق گیری از تابع کسری رادیکالی با رابطه مشتق تقسیم دو تابع
بر اساس رابطه مشتق توابع کسری، داریم:
$$ \frac { d } { d x } \left [ \frac { f ( x ) } { g ( x ) } \right ] = \frac { g ( x ) f' ( x ) - f ( x ) g' ( x ) } { [ g ( x ) ] ^ { ۲ } } $$
صورت تابع مورد سوال را برابر با $$ f ( x ) $$ و مخرج آن را برابر با $$ g ( x ) $$ قرار میدهیم:
$$ f ( x ) = \sqrt [۳] { x } $$
$$ g ( x ) = \sqrt { x } $$
اکنون، از این دو تابع، مشتق میگیریم. مشتقهای این توابع، با استفاده از رابطه زیر به دست میآیند:
$$
f ' ( x ) = { \left ( { \sqrt [ \large ۳ \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۳ – ۱ } } } } } } } = \frac {۱}{۳\sqrt [۳] { x ^ ۲ }}
$$
$$
g ' ( x ) = { \left ( { \sqrt [ \large ۲ \normalsize ] { x } } \right ) ^ \prime } = { \frac { ۱ } { { ۲ \sqrt [ \large ۳ \normalsize ] { { { x ^ { ۲ – ۱ } } } } } } } = \frac { ۱ } { ۲ \sqrt{ x }}
$$
این مشتقها را به همراه توابع اولیهشان درون فرمول مشتق تقسیم قرار میدهیم:
$$
\frac { d } { d x } \left [ \frac { \sqrt [۳] { x } }{ \sqrt { x }} \right ] = \frac { \sqrt { x } \times \frac {۱}{۳\sqrt [۳] { x ^ ۲ }} - \sqrt [۳] { x } \times \frac { ۱ } { ۲ \sqrt{ x }} } { ( \sqrt { x } ) ^ { ۲ } }
$$
پس از ضرب کردن عبارتهای صورت، گرفتن مخرج مشترک و سادهسازی، به جواب زیر میرسیم:
$$
\frac { d } { d x } \left [ \frac { \sqrt [۳] { x } }{ \sqrt { x }} \right ] = - \frac { ۱} { ۶x \sqrt [۶] { x } }
$$
مشتق گیری از تابع کسری رادیکالی با رابطه مشتق عبارت توانی
برای اینکه بتوانیم از رابطه مشتق توابع تواندار برای تعیین مشتق تابع مورد سوال استفاده کنیم، ابتدا آن را به صورت زیر بازنویسی و سادهسازی میکنیم:
$$
\frac { \sqrt [۳] { x } }{ \sqrt { x }} = \frac { x ^ { \frac { ۱ }{ ۳ } } }{x ^ { \frac { ۱ }{ ۲ } } }
$$
$$
\frac { \sqrt [۳] { x } }{ \sqrt { x }} = x ^ { \frac { ۱ }{ ۳ } } \times x ^ { - \frac { ۱ }{ ۲ } }
$$
$$
\frac { \sqrt [۳] { x } }{ \sqrt { x }} = x ^ { \frac { ۱ }{ ۳ } - \frac { ۱ }{ ۲ } }
$$
$$
\frac { \sqrt [۳] { x } }{ \sqrt { x }} = x ^ { - \frac { ۱ }{ ۶ } }
$$
اکنون، کافی است مشتق $$ x ^ { - \frac { ۱ }{ ۶ } } $$ را به دست بیاوریم. به این منظور، داریم:
$$
\frac { d } { d x } \left ( x ^ { - \frac { ۱ }{ ۶ } } \right ) = - \frac {۱}{۶} x ^ {\left (- \frac {۱}{۶} - ۱ \right) }
$$
$$
\frac { d } { d x } \left ( x ^ { - \frac { ۱ }{ ۶ } } \right ) = - \frac {۱}{۶} x ^ { - \frac {۷}{۶} }
$$
$$
\frac { d } { d x } \left ( x ^ { - \frac { ۱ }{ ۶ } } \right ) = - \frac {۱}{۶ x ^ { \frac {۷}{۶}}}
$$
در نتیجه:
$$
\frac { d } { d x } \left [ \frac { \sqrt [۳] { x } }{ \sqrt { x }} \right ] = - \frac {۱}{۶ x ^ { \frac {۷}{۶}}}
$$
نتیجه به دست آمده، فرم توانی $$ - \frac { ۱} { ۶x \sqrt [۶] { x } } $$ است.

تمرین ۲: مشتق تفریق دو تابع رادیکال با فرجه ۳ و فرجه های بالاتر
حاصل مشتق زیر را به دست بیاورید:
$$
\frac { d } { d x } \left ( \sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \:-\: \sqrt [ ۴ ] { \ln \left ( x \right ) } \right )
$$
این تمرین، مشتق تفریق دو تابع رادیکالی را از ما میخواهد. بر اساس قوانین مشتقگیری، مشتق جمع/تفریق دو تابع، با جمع/تفریق مشتقهای آن دو تابع برابری میکند. بنابراین میتوانیم مشتق بالا را به صورت زیر بنویسیم:
$$
\frac { d } { d x } \left ( \sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \:-\: \sqrt [ ۴ ] { \ln \left ( x \right ) } \right ) = \frac { d } { d x } \left ( \sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \right ) - \frac { d } { d x } \left ( \sqrt [ ۴ ] { \ln \left ( x \right ) } \right )
$$
به منظور تعیین حاصل مشتق $$ \frac { d } { d x } \left ( \sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \right ) $$، از قاعده مشتقگیری زنجیرهای و مشتق چندجملهای کمک میگیریم. بر اساس این قاعده، داریم:
$$
\frac { d } { d x } \left (\sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \right ) = \left ({ \frac { ۱ } { { ۳ \sqrt [ \large ۳ \normalsize ] { { { (۲ x ^ ۳ + ۵ ) ^ { ۲ } } } } } } } \right ) \left ( ۶ x ^ ۲ \right )
$$
$$
\frac { d } { d x } \left (\sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \right ) = { \frac { ۲ x ^ ۲ } { { \sqrt [ \large ۳ \normalsize ] { { { (۲ x ^ ۳ + ۵ ) ^ { ۲ } } } } } } }
$$
برای به دست آوردن مشتق $$ \frac { d } { d x } \left ( \sqrt [ ۴ ] { \ln \left ( x \right ) } \right ) $$، به رابطه مشتق زنجیرهای و مشتق لگاریتم نیاز داریم:
$$
\frac { d } { d x } \left ( \sqrt [ ۴ ] { \ln \left ( x \right ) } \right ) = { \frac { ۱ } { { ۴ \sqrt [ \large ۴ \normalsize ] { { { \ln ^ { ۳ }( x ) } } } } } } \times \frac { ۱ } { x }
$$
$$
\frac { d } { d x } \left ( \sqrt [ ۴ ] { \ln \left ( x \right ) } \right ) = { \frac { ۱ } { { ۴ x \sqrt [ \large ۴ \normalsize ] { { { \ln ^ { ۳ }( x ) } } } } } }
$$
به این ترتیب، جواب مشتق مورد سوال برابر است با:
$$
\frac { d } { d x } \left ( \sqrt [ ۳ ] { ۲ x ^ ۳ + ۵ } \:-\: \sqrt [ ۴ ] { \ln \left ( x \right ) } \right )
= { \frac { ۲ x ^ ۲ } { { \sqrt [ \large ۳ \normalsize ] { { { (۲ x ^ ۳ + ۵ ) ^ { ۲ } } } } } } }
- { \frac { ۱ } { { ۴ x \sqrt [ \large ۴ \normalsize ] { { { \ln ^ { ۳ }( x ) } } } } } }
$$
تمرین ۳: مشتق رادیکال سینوس به توان ۲ با فرجه ۵
مشتق تابع زیر را تعیین کنید:
$$
f ( x ) = \sqrt [۵] {\sin ^ ۲ ( x )}
$$
تابع $$ f ( x ) $$، یک تابع رادیکالی با تابع مثلثاتی سینوس در زیر رادیکال است. روشهای مختلفی برای به دست آوردن مشتق این تابع وجود دارد. با این وجود، در اینجا، از فرمول کلی مشتق تابع رایکال با فرجه ۳ و فرجه های بالاتر استفاده میکنیم. این فرمول عبارت است از:
$$
\frac { d } { d x } \left ( \sqrt [ n ] { u ^ m ( x ) } \right ) = \frac { m \times u ^ { \prime } ( x ) }{ n \sqrt [ n ] { u ^ { n - m } ( x )}}
$$
بر اساس این فرمول و تابع $$ f ( x ) $$ داریم:
$$ u ( x ) = \sin ( x ) $$
$$ u ' ( x ) = \cos ( x ) $$
$$ n = ۵ $$
$$ m = ۲ $$
در نتیجه:
$$
\frac { d } { d x } \left [ \sqrt [۵] {\sin ^ ۲ ( x )} \right ] = \frac { ۲ \times \cos ( x ) }{ ۵ \sqrt [ ۵ ] { \sin ^ { ۵ - ۲ } ( x )}}
$$
$$
\frac { d } { d x } \left [ \sqrt [۵] {\sin ^ ۲ ( x )} \right ] = \frac { ۲ \cos ( x ) }{ ۵ \sqrt [ ۵ ] { \sin ^ { ۳ } ( x )}}
$$
سوالات متداول در رابطه با مشتق رادیکال با فرجه ۳
در بخش آخر این مطلب از مجله فرادرس، به برخی از پرتکرارترین سوالات مرتبط با مبحث تعیین مشتق رادیکال با فرجه ۳ و فرجه های بالاتر به طور خلاصه پاسخ میدهیم.
فرمول مشتق رادیکال x چیست؟
مشتق رادیکال x (با فرجه ۲)، برابر با ۱ بر روی ۲ در رادیکال x است.
مشتق رادیکال ایکس با فرجه ۳ چیست؟
مشتق رادیکال ایکس با فرجه سه برابر با ۱ بر روی ۳ در رادیکال x به توان ۲ با فرجه ۳ است.
روش های تعیین مشتق رادیکال با فرجه ۳ و فرجه های دیگر چیست؟
مشتق توابع رادیکالی با فرجه ۳ و فرجههای دیگر با استفاده از روابط مخصوص، قاعده مشتقگیری زنجیرهای یا فرمول مشتق توابع تواندار به دست میآید.










